Rep:Mod:pikachu
Module 3
Vivien Tang
Introduction
In module 3, transition states in larger molecules were characterized on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. For these larger structures, molecular mechanics force field methods generally cannot be used as they do not take in to account the formation and breaking of bonds, and changes in bonding type and electron distribution. Therefore molecular orbital based methods were used instead, to numerically solve the Schrodinger equation and to locate the transition state structures based on the shape of a potential energy surface. Reaction paths and barrier heights were also calculated.[1]
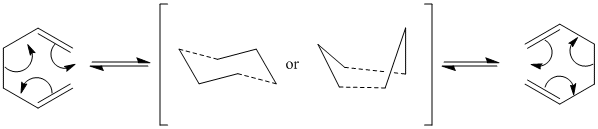
Cope re-arrangement of 1,5-hexadiene
The Cope Rearrangement is a classical pericyclic reaction, the [3,3]-sigmatropic rearrangement of a 1,5-diene. In this example 1,5-hexadiene is used, and the outcome of this reaction is a sigma bond shifting 3 carbon positions. The reaction is thermally allowed via Huckel topology with suprafacial components and a 4n + 2 electron count. The reaction occurs via a concerted mechanism (figure 1), and proceeds via an aromatic transition state which has been found to resemble either the chair or boat form. It has been reported in literature that the boat transition state is higher in energy than the chair conformer.[2] The mechanism of this reaction can be rationalised by using Gaussian to obtain the low energy minima and transition structures on the C6H10 potential energy surface, to confirm that the boat conformer is higher in energy, as the B3LYP method with the 6-311G(d) basis set produces activation energies and enthalpies that correspond closely with experimental data.
Figure 1: Cope re-arrangement of 1,5-hexadiene
Optimizing the reactants and products
HFT/3-21G optimization
In order to rationalize the mechanistic pathway of the Cope re-arrangement, the minimum energy conformation of 1,5-hexadiene was found (since the reactant and product of this reaction are indistinguishable). An initial optimization of the 1,5-hexadiene in 'gauche' and 'anti' starting conformations was carried out using the HFT method and low level basis set 3-21G. The 'gauche' and 'anti' labels given to the conformers refer to the four central carbons in the molecule, where a 45 degree dihedral angle qualifies a 'guache' conformer, whilst an 180 degree dihedral angle produces an 'anti' conformer. Several of each were modelled, as the angle of the terminal groups on the molecule could be varied. The 'symmetrize' function was used to obtain the point groups of the conformers modelled. Table 1 summarizes the symmetry and final energies of the optimized conformers.
Table 1: Anti and Gauche conformers
| Conformer | Image | Point Group | Energy/Hartrees HF/3-21G |
Relative Energy/kcal/mol | Link to D-space file |
| anti 1 | C2h | -231.68907 | 2.25 | DOI:10042/to-10061 | |
| anti 2 | C1 | -231.69092 | 1.06 | DOI:10042/to-10062 | |
| 'anti 3' | Ci | -231.69253 | 0.08 | DOI:10042/to-10063 | |
| 'anti 4' | C2 | -231.69260 | 0.04 | DOI:10042/to-10064 | |
| 'gauche 1' | C1 | -231.69266 | 0.00 | DOI:10042/to-10065 | |
| gauche 2 | C1 | -231.68916 | 2.20 | DOI:10042/to-10066 | |
| gauche 3 | C1 | -231.69167 | 0.62 | DOI:10042/to-10067 | |
| gauche 5 | C2 | -231.69153 | 0.71 | DOI:10042/to-10068 | |
| gauche 6 | C1 | -231.68961 | 1.91 | DOI:10042/to-10069 |
When considering the steric hindrance caused by the proximity of the terminal alkene groups, it would be expected that the lowest energy structure would be an anti conformer, due to the 180 degree dihedral angle that place the alkene groups as far away from each other as possible. Furthermore, the anti conformer is expected to have a lower total energy as there is a greater degree of orbital overlap between the C/C-H σ-orbital and the C-C/C-H σ*-orbitals [3], than for a gauche conformer. However, the gauche conformations allow for additional H-H van der waal's stabilizing interactions between the hydrogens of non-adjacent carbons (within the attractive Van der Waals region of around 2.1-2.4 Å)[4] From table 1, it can be seen that 'gauche 1' is the lowest energy conformer, as it has the shortest H-H van der waals distances of all the gauche conformations. Aside from the factors mentioned previously, the stability of gauche 1 can also be explained in terms of hyperconjugation and interaction of the allyl groups. The 3-21G basis set was used to computate the MOs of the gauche 1 conformer, and also the MOs of other low energy conformers anti 3 and anti 4 for comparison (figure 2).
 |
 |
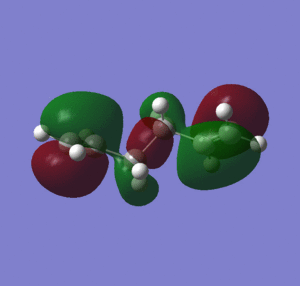 |
Figure 2 shows that for the gauche 1, the energy of the HOMO is lower than for the other conformers. It can also be seen that for gauche 1 there is conjugation between the two terminal pi bonds, which stabilizes the conformation (no overlap can be observed between the vinyl hydrogens and the pi system), which is not observed for the HOMO of anti 3 and anti 4.
B3LYP/6-31G(d) re-optimization
The lowest energy conformers, gauche 1, anti 3 and anti 4, were re-optimized at a higher level of theory using B3LYP and basis set 6-31G(d)(table 2). The results show that the B3LYP method produces a lower energy after optimization than the HFT method, stabilising the conformers by around 3au. The difference in results arises from the number of approximations used in the computation of the molecular orbitals, that affects the computation of the intramolecular orbital interactions. For example, in the gauche 1 conformation, the stabilising effect is partially due to the interaction between the vinyl hydrogen and the pi orbital, thus the strength of the interaction depends on the orbital size, which is dependent on the method and basis set used. Table 2 shows that with the higher level of theory used, the conformer anti 3 is lower in energy than the gauche 1 conformer. The anti 3 conformer with Ci symmetry is used to compare how the geometry of the molecules is affected by using different methods and basis sets, by comparing bond angles, dihedral angles and bond lengths (table 3).
Table 2: Optimization of geometries using B3LYP/6-31G(d)
| Conformer | Image | Point Group | Energy/Hartrees | Link to D-space file |
| gauche 1 | C1 | -234.61133 | DOI:10042/to-10112 | |
| anti 3 | Ci | -234.61171 | DOI:10042/to-10113 | |
| 'anti 4' | C2 | -234.61179 | DOI:10042/to-10115 |
| Method | C=C bond length/A | C-C bond length/A | C1-C4 dihedral angle/degrees | C2-C5 dihedral angle/degrees | C3-C6 dihedral angle/degrees | H-C1-C2 angle |
|---|---|---|---|---|---|---|
| HF | 1.31616 | 1.50892 | -114.64 | 179.98 | 114.67809 | 121.82 |
| B3LYP | 1.33352 | 1.50421 | -118.59 | -180.00 | 118.58758 | 121.65 |
As mentioned previously, the conformer anti 3 is lower in energy than the gauche 1 conformer when optimized using a higher level of theory. This extra stabilization may be attributed to better overlap of the C/C-H σ-orbital and the C-C/C-H σ*-orbitals when using the B3LYP method, as table 3 shows that the C2-C5 dihedral angle is 180 degrees compared with 179.98 degrees for the HF optimization, thus maximizing the overlap. For the B3LYP optimization, the bond lengths are slightly longer, and the C1-C4 dihedral angle and C3-C6 dihedral angle are greater. However, the changes to the geometries are very small when using a higher level of theory. It can be seen from the computationally determined MOs that for the gauche 1 coformer, even with the higher level of theory there is still conjugation between the two terminal pi bonds that is absent from the other conformers, and so the weighting of this stabilizing effect has decreased relatively upon using a higher level of theory for optimization.
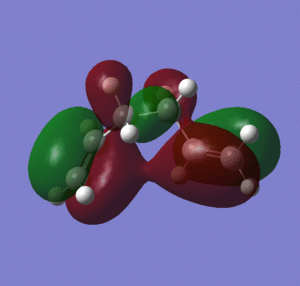 |
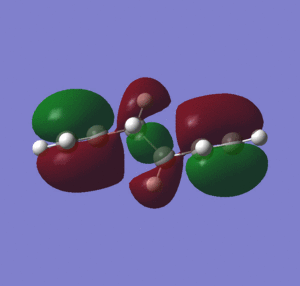 |
Vibrational analysis of anti 3
A frequency analysis using the same level of theory, B3LYP, and basis set, 6-31G(d), was carried out to confirm that the structures obtained after optimization were at ground state, rather than transition states. This is because the vibrational analysis essentially calculates the second derivative of the potential energy surface, so it can be determined whether turning points obtained by the optimization calculation are maxima (transition states) or minima (ground states). Since the vibrational analysis for 1,5 hexadiene returned no negative values, or imaginary vibrations, this indicates that the optimization was a minimum energy conformation. The low frequencies found in the log file of the analysis were close to zero, supporting the accuracy of the analysis:
Low frequencies --- -9.4830 -0.0002 -0.0001 0.0004 3.7550 13.0195
and the computationally determined spectrum was close to that of literature values[5].
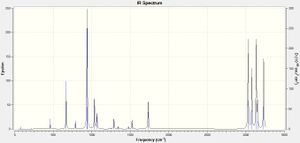 |
Thermodynamic data
The frequency analysis allowed several thermochemical properties to be calculated: -the sum of electronic and zero-point energies (E = Eelec + ZPE): the potential energy of a molecule at 0K and the contribution from vibrational zero point energy. -The sum of electronic and thermal energies (E = E + Evib + Erot + Etrans): the energy of a molecule at 298.15 K and 1 atm, including translational, rotational and vibrational energy contributions. - The sum of electronic and thermal enthalpies (H = E + RT): this is the energy of a molecule including a correction for the thermao energy. -The sum of electronic and thermal free energies (G = H - TS): this energy includes the entropic contribution to free energy.
The output for the vibrational analysis gives these thermochemical properties at 298.15K, but the values were also recalculated for 0K by including the key word Freq=ReadIsotopes into input file, and manually adjusting the input temperature to be 0.0001K.
| Thermochemical Data / Eh (a.u) | ||
| 298.15 K | 0 K | |
| Sum of the Electronic and Zero-Point Energies |
-234.469204 | -234.468758 |
| Sum of Electronic and Thermal Energies |
-234.461857 | -234.468758 |
| Sum of Electronic and Thermal Enthalpies |
-234.460913 | -234.468758 |
| Sum of Electronic and Thermal Free Energies |
-234.500777 | -234.468758 |
The comparison shows that the thermal contributions at 0K are zero, and so all the values at 0K are the same as the sum of the electronic and zero point energies. It can also be observed that the sum of electronic and thermal free energies is smaller for 298.15K, which reflects greater stability for the anti 3 conformer at higher temperatures.
Optimizing the 'chair' and 'boat' transition structures
In this section a transition structure optimization was set up using three methods. The chair transition structure was optimized by computing the force constants at the start of the calculation, and the redundant coordinate editor was used for the frozen coordinate method. For the boat transition structure, QST2 was used. The reaction coordinate was visualized and the Intrinsic Reaction Coordinate was run. The activation energies for the Cope re-arrangement via the 'chair' and 'boat' transition structures were calculated.
Optimization of the 'chair' transition structure
An allyl fragment was firstly drawn, and then optimized with the HF method and 3-21G basis set.
 |
The optimized allyl fragment was pasted into a new molecule window and the terminal ends of the allyl fragments placed 2.20 Å apart, to form a guessed structure of the chair transition state. Two different methods were used to optimize the chair geometry, depending on how close the guessed structure is to the transition state. The first method was to carry out an optimization and frequency analysis using HF method and 3-21G basis set. The Opt+Freq option was used, with the additional keywords Opt=noeigen added to prevent failure of the calculation if more than one imaginary frequency was found. Instead of optimizing to the minimum (as was done previously to find the lowest energy conformation), the guessed structure was optimized with a Berny optimization to a transition state. The force constants were only calculated once.
The second method was to optimize using the frozen coordinate method. The Redundant Coordinate Editor was used to freeze the coordinates of two of the terminal carbons from the allyl fragments which form or break a bond during the rearrangement at 2.2 Å. The structure was then optimized as if it were a minimum with the keywords Opt=ModRedundant. The optimized structure appears very similar to the transition optimized with the first method, apart from the bond forming and breaking distances set to 2.2 Å. The Redundant Coordinate Editor was used again to optimize these bond distances, and this time the transition state optimization was carried out without calculating the force constants. Instead, a normal guess Hessian modified to include the information about the two coordinates being differentiated along was used. The final optimized structure using the frozen coordinate method was compared with the first in table 3.
| Method | Calculation of force constants | Frozen coordinate method |
|---|---|---|
 |
| |
 |
|
The single negative frequency of around -817cm-1 shows that the optimized structures were transition states, which is concordant with the reference imaginary frequency for the Cope rearrangement. The form of vibration for this imaginary frequency shows two terminal carbons bending towards each other, whilst the other pair of terminal carbons simultaneously bend away from each other, reflecting the simultaneous bond breaking and bond formation of the Cope rearrangement. The optimized structures produced for both methods were very similar, as the difference in energies and bond lengths were negligible, smaller than the accuracy for the values. The frozen coordinate method of optimization is slower than the force constant calculation method, as multiple steps of optimization are required. The frozen coordinate method also requires sound understanding of the reaction mechanism, as bond distances must be fixed, but the method is more reliable for instances where the guessed structure is not accurate enough to converge at the first stage.
Optimization of the 'boat' transition structure
The QST2 method was employed to optimize the 'boat' transition state structure. The reactants and products were specified for the reaction, and the calculation interpolated between the two structures to try to obtain the transition state between them. Therefore the reactants and products were numbered in the same way, as shown below:
 |
 |
An Opt-freq calculation was then carried out using the TS(QST2) method, (retaining the use of the B3LYP method and 6-31G(d) basis set used to previously optimize the anti 3 reactant conformers) and the desired boat transition state structure was not reached, as shown below:
 |
The failed optimization looks similar to the chair transition structure, but is more dissociated. This is because when the calculation linearly interpolated between the two structures, it translated the top allyl fragment and did not take into consideration the possiblity of rotation around the central bonds. The reactant and product geometries were then adjusted so that they more closely resembled the boat transition structure. The C2-C3-C4-C5 dihedral angle for the reactant molecule was adjusted to 0 degrees, and the C2-C3-C4 and C3-C4-C5 angles were adjusted to 100 degrees. This was repeated for the product molecule.
 |
 |
The output for the optimization fully converged into the boat transition state structure. The optimization was then carried out with QST3 and the two outputs compared. The QST3 method is considered to be more reliable, and was able to generate the boat transition state structure from the original reactant and product molecules, with one additional structure added to the molgroup which resembles the TS.
| Method | QST2 | QST3 DOI:10042/to-10218 |
|---|---|---|
 |
| |
 |

|
The two methods give very similar results, but the advantage of QST3 is that the optimization is less likely to fail as the 'guessed' structure does not have to be so close to the transition state. The C-C bond distances for the partially formed bonds are 2.20527 Å and the energy of the optimized structure using QST2 is 231.60280186 a.u. These values are higher than the for the chair conformer, as the allyl fragments to form the boat structure contain eclipsed central carbon atoms, increasing steric clashes that raise energy. The single negative frequency calculated for the boat transition structure was lower than for the chair structure, which indicates that the bonds are weaker, further supporting the statement that the chair structure is more stable than the boat. The form of vibration for the negative frequency once again shows the concerted formation and breaking of C-C bonds.
Intrinsic reaction coordinate method
It is extremely difficult to predict which conformer of the 1,5 hexadiene the transition state leads to by simply observing it. A technique that allows the path of the reaction along the potential energy surface to be followed must be used, so that the conformation of the product and the reactant can be observed. Such a technique is called the Intrinsic Reaction Coordinate method (IRC, which works by creating a series of points by taking small geometry steps in the direction where the gradient of the potential energy surface is steepest; essentially the method extrapolates from an imaginary vibration to a lower energy local minimum, which is the probable conformation of the molecule that undergoes the Cope re-arrangement via the chair transition state.
The chair transition state optimized with the frozen coordinate method was used to employ the IRC method. The number of steps was changed to '50', and only the forward reaction was run as the reaction coordinate for the Cope re-arrangement is symmetrical, but the calculation failed to reach a minimum geometry:
 |
 |
Only 24 points are present on the graphs, and so the transition state was not able to be optimized to the 1,5-hexadiene product. A reason for this could be that the calculation did not follow the correct path on the potential energy surface, therefore the IRC could be run again, but with the force constants being calculated at every step. This is a more reliable way of reaching the minimum geometry than taking the last point on the IRC and running a normal minimization, or restarting the IRC with a larger number of points specified, as these methods can lead to the wrong minimum. However, calculating the force constants at every step can be the most computationally demanding, and may not be feasible for very large systems, but the chair transition state structure being investigated for this exercise does not contain many electrons, so the calculation was successful.
 |
 |
The graphs show that the calculation terminated at 47 steps, but was successful at reaching a minimum geometry. The energy of the final structure was -231.69166 au, and the symmetry was C2, indicating that the chair transition state structure is connected to the gauche 3 conformer, as the symmetry and energy are concordant. Jmol of the minimum energy structure after IRC calculation
 |
The same successful IRC method was applied to the QST2 optimized boat transition state structure. The results are shown below:
 |
 |
The graphs show that the calculation terminated at 51 steps, and was successful at reaching a minimum geometry. The energy of the final structure was -231.69266 a.u and the symmetry C1, which corresponds with the Gauche 1 conformer.
 |
Calculating activation energies
The activation energy for the Cope Rearrangement can be calculated by finding the difference between the ground state 1,5 hexadiene and the transition state structure energies. In this way, the different activation energies for the reaction to proceed via the boat or chair transition state can be compared. The anti Ci conformer is used as the ground state molecule.
For this exercise, the HF/3-21G method and basis set were compared with the B3LYP/6-31G(d) for optimization of the ground and transition state structures. Whilst the two produce similar optimized geometries, the energies calculated with a higher level of theory are significantly different. To calculate the activation energies at 0K, the zero point energies in the thermochemistry section of the log file for vibrational analysis were used.
Table 7:Calculating activation energies
| Chair TS with HF/3-21G | Boat TS with HF/3-21G | Chair TS with B3LYP/6-31G(d) | Boat TS with B3LYP/6-31G(d) | |
|---|---|---|---|---|
| Zero point energy (a.u) | -231.466701 | -231.450926 | -234.414933 | -234.402334 |
| Zero point energy of 1,5 hexadiene (anti 3 Ci) (a.u) | -231.539540 | -231.539540 | -234.469204 | -234.469204 |
| Difference in energy (a.u) | 0.072840 | 0.088620 | 0.054270 | 0.066860 |
| Difference in energy (kcal/mol) | 45.71 | 55.61 | 34.05 | 41.95 |
The literature values[6] of 33.5 ± 0.5 kcal/mol for the chair transition state and 44.7 ± 2.0 kcal/mol for the boat transition state do not agree well with the activation energies calculated with the HF method. However, the agreement was better with B3LYP/6-31G(d), as the values calculated are quite close, considering the degree of error in the literature. This reflects how the accuracy increases significantly when a higher level of theory is employed. The chair transition state is therefore 7.90 kcal/mol lower than the boat transition state. Since the reactants and products are equally stable due to their identical structures, it can be concluded that it is favourable for the Cope Rearrangement to proceed via the less energetic chair transition state, and will twist into the gauche 2 C2 conformer to do this.
One explanation as to why the chair transition state is lower in energy than the boat is that there is a secondary orbital interaction between the HOMO and LUMO orbitals of two allyl fragments in the boat transition state which is anti bonding in nature, thus destabilizing the transition state relative to the chair, where no such interaction is possible.<I Fleming, 'Frontier Orbitals and Organic Chemical Reactions', 1st edition, 1976, pp5-10 </ref>
The Diels Alder cycloaddition
The Diels Alder cycloaddition is a pericyclic reaction involving two π systems, where one contributes 4π electrons and the other 2π electrons. The total electron count is 6(4n+2, n=1) and the reaction proceeds under thermal conditions via Huckel topology involving only suprafacial components. The endo form of the product, an isomer where the bonds form to the bottom face of the alkene is predicted to be more stable (as a transition state) than the exo form.[7]
In the Diels Alder reaction, new σ bonds are formed with the π orbitals of the diene and the π orbitals of the dienophiles. If the HOMO of one reactant interacts with the LUMO of the other reactant, then the reaction is allowed. The reaction is forbidden when the orbitals involved have different symmetry properties, as then no overlap in density is possible. If substituents are present on the dienophile, the π orbitals of the substituents can interact with the new double bond being formed in the product, and this interaction can stabilize the regiochemistry of the reaction.
In this section, the nature of the transition structure for the Diels Alder reaction was studied, for a simple reaction between cis-butadiene and ethylene, and then in a more complicated reaction where diene and dienophile include substituents, and where secondary orbital interactions should be considered.
Reaction between cis-butadiene and ethylene
 |
The reaction between cis-butadiene and ethylene was firstly considered, where the reactants do not support additional substituents, and so only one transition state exists. Both structures were optimized using the semi-empirical AM1 method. The MOs for each were calculated to determine whether they were symmetric or antisymmetric with respect to the plane.
table 8: Visualizing MOs
With respect to a vertical plane of symmetry down the centre of each of these MOs, the table shows that the reaction is allowed as the HOMO of the cis-butadiene and the LUMO of the ethylene are of the same symmetry, and so are the LUMO of the cis-butadiene and the HOMO of the ethylene. It can be seen that the HOMO and LUMO of the cis-butadiene are formed by the combination of π and π* orbitals. However, the transition state of the reaction must be modelled in order to determine which HOMO interacts with which LUMO.
Modelling the transition state
The optimized cis-butadiene and ethylene fragments were used to model the transition state for this Diels-Alder reaction. The guessed structure was set up by setting the distance between the fragments as 2.20 Å. This was optimized using the redundant coordinate editor to freeze the reaction coordinates, and then an optimization and frequency analysis was carried out to gain the optimized transition state, and to confirm that the structure was indeed a transition state. The final optimized structure is shown below:
 |
The frequency analysis confirmed the nature of the optimized structure as a transition state as one negative value was returned in the output. This imaginary vibration was at -817.52cm-1 and the form of vibration indicated the formation of a bond between the ethylene and cis-butadiene carbons. The imaginary vibration also indicated that the Diels-alder cycloaddition is a concerted reaction, as the bond formation between the carbons is synchronised. In comparison, the lowest positive frequency for the transition state was at 165.36 cm-1 and the form of vibration showed the ethylene in a wagging motion beneath the cis-butadiene fragment, which does not correspond to bond formation or breaking.
 |
 |
The partly formed σ C-C bonds have a bond distance of 2.21Å, whereas typical sp3 C-C bond lengths are 1.544Å and for sp2 it is 1.338Å. Furthermore, the literature value for the Van der Waals radius of carbon is 1.70Å. The relatively long bond distance of 2.21Å therefore reflects the partially formed nature of the bonds in the transition state. Additionally, the C=C bond of the ethylene fragment in the TS is 1.38Å, the bond length of the C-C in the butadiene fragment of the TS is 1.39Å and 1.37Å for the C=C of the butadiene fragment. These bond lengths intermediate of sp2 and sp3 literature[8] bond lengths suggests that π-bonding of the reactants is being disturbed, and so the hybridisation of the carbons is changing.
Table 9: Visualizing MOs
| HOMO-1 | HOMO | LUMO | |
|---|---|---|---|
| Computed MOs |  |
 |
 |
| LCAO MOs | 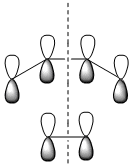 |
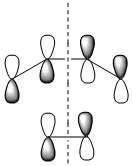 |
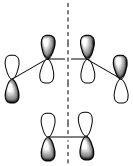 |
| Symmetry with respect to the plane | symmetric | antisymmetric | symmetric |
The HOMO is antisymmetric with respect to the plane, indicating that the two C-C σ-bonds were formed from the overlap of the antisymmetrical HOMO of cis-butadiene with the antisymmetric LUMO of ethylene. The LUMO of the transition state is conversely formed from the overlap of the symmetric HOMO of ethylene and the symmetric LUMO of cis-butadiene. The suprafacial overlap of the orbitals in the HOMO is concordant with the pericyclic selection rules, which dictate that systems containing 4n +2 electrons proceed via a Huckel transision state and contain suprafacial components.
Regioselectivity of the Diels Alder Reaction
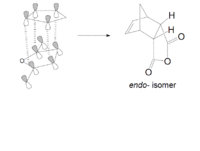
In the Diels-Alder reaction between ethylene and cis-butadiene, there are no additional substituents on the reactant molecules and so there are no selectivity problems. For the reaction between cyclohexa-1,3-diene with maleic anhydride, the regioselectivity of the Diels-Alder reaction can be studied. For this reaction, the endo product is preferentially formed over the exo product, and result can be explained by considering secondary orbital interactions. The reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy.
Figure 16
 |
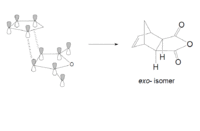 |
The overlap of orbitals that are not involved in the formation of the two new σ-bonds during the Diels-Alder cycloaddition are known as the secondary orbital interactions. As shown below, these are possible when the reactants approach each other to form the endo-adduct. The secondary orbital overlap thus gives the endo transition state additional stabilization over the exo form, and so the formation of the endo-adduct is preferred.
The transition states for the endo and exo adducts were modelled. Firstly, the reactants cyclohexa-1,3-diene and maleic anhydride were optimized with the semi-empirical method AM1, and the resultant structures were used to calculate the endo and exo transition structures using the AM1 semi-empirical method with the freeze coordinate technique, followed by taking derivatives along the C-C bonds being formed. As in the previous exercises, the interatomic distance was set at 2.2 Å. The results are shown below:
The form of vibrations of the imaginary frequencies indicate that both reactions proceed via a concerted mechanism where both bonds are formed at the same time, the norm for a pericyclic reaction.The transition structure that leads to the endo product has a lower energy than the TS structure leading to the exo adduct, which supports the previous observation of the endo adduct being preferentially formed. Steric interactions can be considered when explaining the relative destabilization of the exo transition structure. The main difference between the two isomers is the hybridisation of the carbon atoms above the O=C-O-C=O fragment in the maleic anhydride. This is because in the endo transition state they are sp2 hybridised, but in the exo transition state they are sp3 hybridised. The tetrahedral sp3 carbons in the exo structure are therefore directed towards the maleic anhydride ring, resulting in greter steric repulsion, hence an increased transition state energy, and a larger C-C through space distance. The partially formed σ C-C bonds for the exo transition state are also slightly longer than for the endo structure, but both values are longer than literature[11] values for typical single C-C bonds (1.54 Å) and typical C=C double bonds (1.34Å), but smaller than the combined Van der Waals radii of two carbon atoms (3.40Å). This indicates that a bond is in the process of being formed between the two atoms.
Table 11: Summarize bond lengths in the endo/exo transition states
| Partially formed C-C (Å) | C=C (Å) | C-C (Å) | Through space C-C (Å) | |
|---|---|---|---|---|
| Endo | 2.17 | 1.39 | 1.40 | 2.95 |
| Exo | 2.29 | 1.39 | 1.49 | 2.98 |
Table 12: MOs calculated for the exo/endo transition states
(I deleted the table from my code by accident, but it was still on one of my computer screens so to save time I copied the image of the lost table)
The MOs of the transition states were visualized, in order to see if any secondary orbital interactions could be observed. These were expected to be a region of delocalized electron density between the cyclohexa-1,3-diene pi orbitals and the carbonyl carbon, which can be observed in the LUMO+1 MO of the endo transition states. Whilst it is difficult to rationalize the stabilization of the secondary orbital interaction with respect to an anti bonding orbital, the energy of the LUMO+1 is slightly lower in energy than the LUMO+1 of the exo transition state.
The secondary orbital interactions also supports the shorter through space C-C distances for the endo transition state over the exo transition state.
To confirm that the correct optimization to transition states had occurred, the IRC for formation of the endo and exo transition states was calculated in the forwards and backwards direction.
 |
 |
 |
 |
 |
|
 |
The IRC calculations show the energy profile of the reaction, from the reactants, through to the transition state and products, confirming the completion of the optimizations.
Conclusion
In conclusion, computational methods were used in this module to model and study transition states. It should be noted that AM1 method is a low level of theory, and so more accurate results could be achieved in future using B3LYP/6-31G(d) instead. Semi-empirical molecular orbital theory approximates some of the integrals used in the solution of Schrodinger's equation, in order to estimate the energy of molecules as a function of the electron distribution and geometry. To compensate for these approximations, empirically derived parameters are introduced to allow calculated results to be in agreement with observed spectroscopic or molecular properties.[12]
References
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ K. C. Nicolaou, 'The Diels ± Alder Reaction in Total Synthesis', Angew. Chem. Int. Ed. 2002, 41, 1668 ± 1698
- ↑ Robert D. Stolow J. Am. Chem. Soc., 1966, 88 (5), pp 1087–1087
- ↑ Kamyar Afarinkia et al.,J. Org. Chem., 2003, 68 (19), pp 7158–7166
- ↑ D. Bloch, Organic Chemistry Demystified, 2006, 28
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/
- ↑ Stoicheff, B.P., Tetrahedron, 1962, 17, 135-145
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ P V. Alston et al.J. Org. Chem., 1975, 40 (8), pp 1111–1116
- ↑ Stoicheff, B.P., Tetrahedron, 1962, 17, 135-145
- ↑ Stoicheff, B.P., Tetrahedron, 1962, 17, 135-145