Rep:Mod:physicalccrossland

Introduction

It is possible to use computational methods to understand the transition structures for many reactions. Gaussian uses quantum mechanical molecular orbital calculations to achieve this. All energies are presented in hartrees (au) unless otherwise stated.

Reaction 1: Cope Rearrangement

Introduction

The cope rearrangement constitutes the [3,3] sigmatropic (thermal activation, suprafacial) rearrangement of 1,5-hexadiene, as shown.

Optimizing Reactants & Products

1,5-hexadiene can adopt two principle dihedral angles about its cental C-C bond, antiperiplanar (APP; where the R groups are at 180 degrees) and Gauche (where they are at 60 degrees). To probe the energy of the APP, 1,5-hexadiene was constructed in Gaussian, and the dihedral angle set to 180. Thereafter, the structure was optimised to the Hartree-Fock (HF) 3-21G level of theory, yielding an energy of -231.69253525 Hartrees, with symmetry Ci. Similar analysis with a Gauche conformation yielded an energy of -231.69266122, with C1 symmetry. This showed the Gauche conformation to be the preferred conformer.

The antiperiplanar conformer was further optimised to the B3LYP/6-31G* level, yielding an energy of -234.61170276 hartrees, and identical treatment of the gauche conformer gave an energy of -234.61068499 hartrees.

Structures
Antiperiplanar	Gauche

E = -231.69253525 (HF)	E = -231.69266122 (HF)
E = -234.61170276 (B3LYP)	E = -234.61068499 (B3LYP)

Optimising the Transition Structure

In order to begin the process of the optimisation of the chair transition state, a simple allyl fragment was constructed and optimised to the HF/3-21G level, yielding the structure shown below.

Two of these allyl fragments were then aligned as shown below, approximating the separation of the terminal carbons to 2.2 Angstroms.

When optimised to the HF/3-21G level, the energy recorded was -231.61932242 hartrees, with point group C1. Further optimisation was carried out using the reaction coordinate freeze method, first by fixing the terminal bond lenghts and then by optimising these, the combination of which yields the fully optimised transition state. The result is shown below.

Chair Transition Structure Optimised by Frozen Coordinate

Next, we can optimise the boat transition state, first using the QST2 method. This method involves the input of the reactants and products, which the software interpolates between to find the transition state. An initial computation using 50 iterations yielded the structure below, clearly a distorted chair transition state. Modification of the reactants and products to more closely resemble the anticipated transition state ensured the structure shown next was achieved, resembling how we would expect the transition state to look. This modification involved setting the central dihedral angle to 0 degrees, and the C-C-C bond angles to 100 degrees.

Distorted Boat Transition Structure by QST2

Boat Transition Structure by QST2 with Bond Angle Adjustment

Summary of Transition State Energies
Chair	Boat
E = -234.55698291	E = -234.54309307

IRC analysis suggests the chair transition state has a gauche conformer precursor, and the boat an APP one. This gives the following activation energies (TS energy - reactant energy).

Gauche-Chair	APP-Boat
33.70 Kcal/mol	43.05 Kcal/mol

These activation values for the chair and boat reaction pathways agree well with experimental values (33.5 & 44.7 Kcal/mol respectively), errors of -0.59 % and 3.69 %.

Reaction 2: The Diels-Alder Cycloaddition

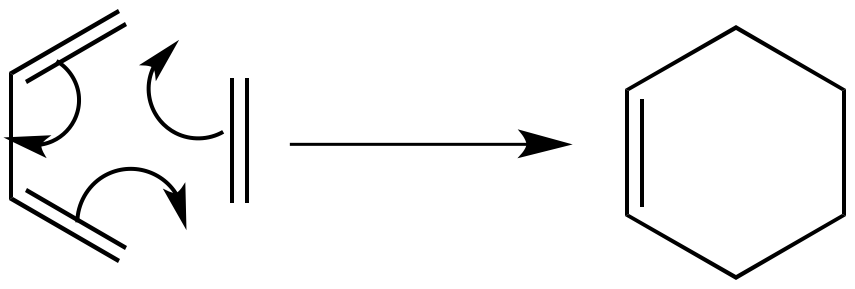
The Diels-Alder reaction is an example of a pericyclic reaction, whereby two new sigma-bonds are formed from existing pi-bonds, via a concerted reaction. The reactants are a conjugated diene (which must be in the s-cis conformation to react) and a dieneophile. Reaction occurs via the interaction of the HOMO of one species with the LUMO of another. The transition state therefore takes the conformation that achieves most efficient overlap of the orbitals (MOs are shown below for ethylene and butadiene) and can also be influenced by secondary orbital interactions if the reactants are substituted, resulting in differing product stereochemistry. A generic example is shown below, the reaction of butadiene and ethylene.

Example 1: Ethylene + Butadiene

Molecular Orbitals
	HOMO	LUMO
Cis-Butadiene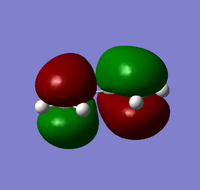
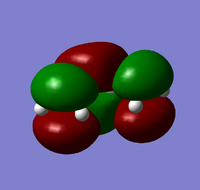
	Antisymmetric	Symmetric
Ethylene
	Symmetric	Antisymmetric

Finding the Transition State

The transition structure for the Diels-Alder reaction is known to have a structure similar to that shown below. In order to optimise the transition state the structure was constructed in Gaussian and optimised.. First, both cis-butadiene and ethylene were independently optimised (by AM1 semi-empirical method), then positioned in the same plane as each other and optimised using again the AM1 semi-empirical method with the terminal bond lengths frozen. Thereafter the bond lengths were set to derivative and the structure below was found, with the vibration shown as well, the transition structure.

Diels-Alder Approximate Transition State

The transition state has the following Molecular orbitals.

HOMO	LUMO

Antisymmetric	Symmetric

Example 2: Cyclohexadiene + Maleic Anhydride

As previously mentioned, substituents upon the reactants cause varying stereochemistry in the products. The following example, of cyclohexadiene and maleic anhydride, forms the endo orientation as the major product. Since this is the thermodynamically less favoured product, the reaction must therefore be under kinetic control with the transition state to the end being the lowest in energy. We will now see if that is indeed the case.

The molecular orbitals of the reactants are as shown below.

MO's
	HOMO	LUMO
Cyclohexadiene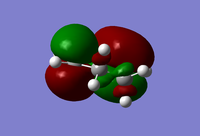
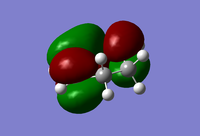
	Antisymmetric	Symmetric
Maleic Anhdride
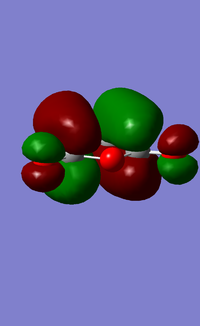
	Symmetric	Antisymmetric

Locating the Endo Transition State

In order to find the end transition state, both the reactants were optimised by the AM1 method, and positioned such that they looked approximately as expected (with the oxygen of maleic anhydride over the cyclohexadiene molecule). The structure was then optimised using the frozen coordinate method and the result is shown below.

Endo Transition State

This transition state has the MO's as follows.

MOs- Endo TS
HOMO	LUMO

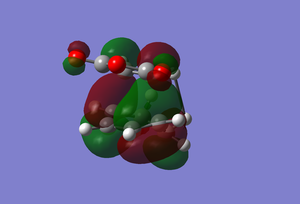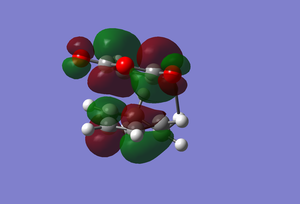
Locating the Exo Transition State

In order to find the exo transition state, the procedure was repeated but with the direction of the maleic anhydride reversed. The result is shown below.

Exo Transition State

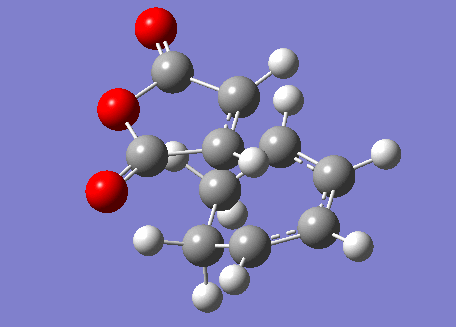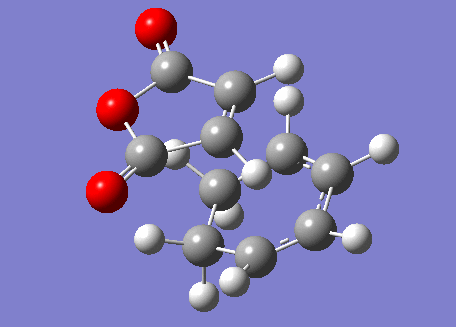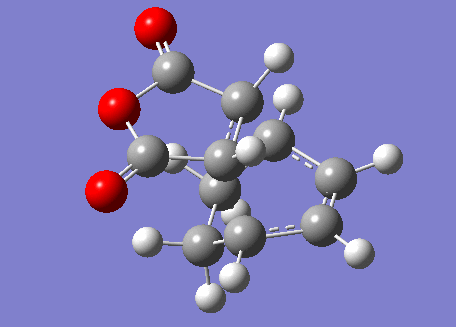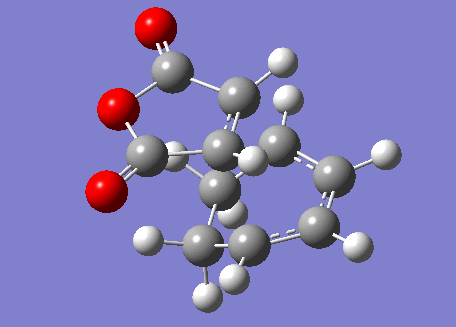
This transition state has the following molecular orbitals.

HOMO	LUMO

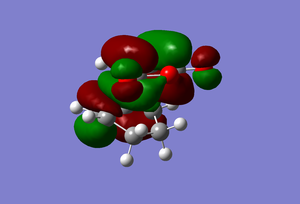
Explanation

The exo and endo transition structures have energies of -0.05041984 and -0.06407816 hartrees, respectively. This clearly shows the endo to be the lower energy transition state, and since this is the major yet thermodynamically unfavoured product, the reaction must be under kinetic control, as hypothesised.

The reason for the favouring of the endo transition state lies in secondary orbital interactions. The pi-system of the carbonyl bonds can interact efficiently with the pi system of the diene in the endo orientation, an effect which is no present in the exo transition state. This serves to stabilise the endo transition state, despite this structure being more sterically demanding.

Conclusion

In this study Gaussian was used to probe the reaction pathways of two different reactions, the Cope rearrangement and the Diels-Alder cycloaddition. The expected major product of the Diels-Alder reaction was rationalised through characterisation of the transition state.

References

Imperial College Labscript (on Wiki) consulted throughout. Clayden's Organic Chemistry used for Diels-Alder section.