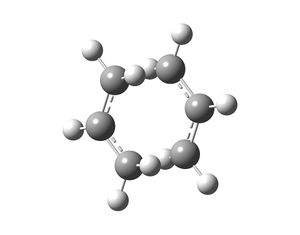
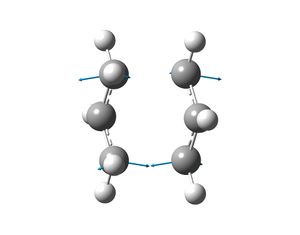
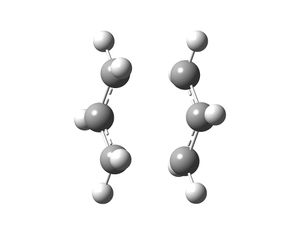
Rep:Mod:physical-pks1927

Module 3 - Physical

Introduction

During a chemical reaction, the reactants can form an activated complex known as a transition state, which has the highest energy value throughout the reaction coordinate. The energy needed to convert reactants into transition states is called the energy barrier or activation energy. In a transition state, bonds are partially broken and formed. The main part of the following investigation is to analyse transition state structures of different reactions. Molecular mechanics models cannot be used to analyse transition state structures and hence will not be used below. This is because molecular mechanics does not describe how bonds are being broken and formed and how bonding and electron distributions change in a reaction. Instead, molecular orbital-based methods are able to analyse transition state structures and thus will be used to find out the transition state structures of reactions, which will in turn help deduce the reaction path and barrier heights.

The Cope Rearrangement

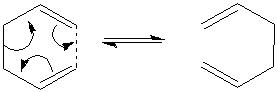
The Cope rearrangement of 1, 5-hexadiene is a [3, 3]-Sigmatropic rearrangement. This rearrangement occurs in a concerted fashion and goes via a chair or boat transition state. The boat transition state should be higher in energy as it is more strained. The aim of this part of the investigation is to identify the low energy minima and the transition state structures of this Cope rearrangement and thus determine the preferred reaction mechanism.

Optimising the Reactants and Products

The reactants and the products of this rearrangement are the same molecule, but just different conformers. Therefore by looking at 1,5-hexadiene and carrying out an optimisation, the reactants and products will both be optimised. There are many stable conformations of 1,5-hexadiene and 10 conformations are shown in Appendix 1.

Part A and B

Anti 1 Results Summary
Dihedral Angle/^o	176.9
Charge	0
Spin	Singlet
Final Energy/a.u.	-231.69260
RMS Gradient/a.u.	0.000019
Dipole Moment/D	0.202
Point Group	C₂

Gauche 1 Results Summary
Dihedral Angle/^o	75.6
Charge	0
Spin	Singlet
Final Energy/a.u.	-231.68772
RMS Gradient/a.u.	0.000017
Dipole Moment/D	0.455
Point Group	C₂

1,5-hexadiene was drawn in Gaussview, in an anti-periplanar conformation. In order to ensure that the linkage was in fact 'anti,' the dihedral angle between C9-C4-C1-C10 was set to 180^o. The molecule was 'cleaned' before being optimised by using Gaussian and the HF/3-21G method and basis set. The calculation ran for 52 seconds and the conformation obtained is shown above. The molecule was also symmetrised and the point group of the molecule was found to be C₂ (see results table). Comparing the results obtained with the values recorded in Appendix 1, it can be seen that the conformer of 1,5-hexadiene obtained after optimisation is anti 1.

For part B 1,5-hexadiene was drawn in Gaussview again, but this time the molecule was drawn in a gauche conformation. To ensure that the gauche conformer was in fact drawn the dihedral angle between C9-C4-C1-C10 was set to 60^o and the molecule again was 'cleaned'. The structure was optimised using the same basis set and method as above, which ensures that comparisons between the different conformers can be made accurately. The calculation took 3 minutes and 22 seconds to process and the results and molecule obtained after the optimisation are shown below. The results were compared with Appendix 1 and it seems that the gauche 1 conformation has been obtained.

As expected the anti conformation is lower in energy than the gauche conformation. The energies differ by 12.8 kJmol^-1. The reason for this is that the carbon double bonds are 176.9^o away from one and other in the anti 1 conformer compared to 75.6^o away from one and other in the gauche 1 conformer. This therefore causes the steric hindrance experienced by the anti conformer to be less than the steric repulsions experienced by the gauche conformer. This is because the electrons in the alkene groups repel one and other and this repulsion increases when the two alkene groups are near one and other. In addition, the overall dipole moment of the anti conformer is less than the gauche conformer and hence the anti conformer is more stable.

Anti-periplanar and gauche conformers of 1,5-hexadiene have been drawn and analysed because these conformers are more likely to be stable compared to the anti-clinal and syn-periplanar conformers. This is because the latter conformations are eclipsed forms, which are high in energy compared to the staggered forms (app and gauche). This is due to the increased steric strain that occurs in the eclipsed forms due to the bond electron-bond electron repulsions. The app and gauche conformers can also be seen to be favoured and more stable due to steroelectronic effects. In both anti-periplanar and gauche conformers, favourable secondary orbital overlap occurs which stabilises the conformation.

Part C

Gauche 3 Results Summary
Dihedral Angle/^o	67.7
Charge	0
Spin	Singlet
Final Energy/a.u.	-231.69266
RMS Gradient/a.u.	0.000012
Dipole Moment/D	0.340
Point Group	C₁

Anti-periplanar conformations generally seem to be the most stable conformers of 1,5-hexadiene due to the large dihedral angle within the molecule, which causes bulky substituents to be placed far away from one and other and thus reduce the steric strain of the molecule. However, in 1,5-hexadiene the most stable conformation is not an app conformer, but the conformer which is gauche with a little app character. Therefore a gauche conformer was drawn in Gaussview and the dihedral angle was not set to 60^o, but to an angle between 60 and 70^o. Again the conformation was optimised using the HF/3-21G method and basis set and the following results were obtained. The gauche conformer was symmetrised and the conformer belongs to the C₁ point group. The results were compared to Appendix 1 and it is found that the gauche 3 conformer has been obtained, which is the most stable conformer. The calculation was quick as it ran for one minute and 34 seconds.

The reason why the gauche 3 conformer has the lowest energy even though the alkene groups are close to one and other in this conformation and hence experience a large amount of steric strain is because of hyper-conjugation and pi-pi interactions.

The HOMO and LUMO of the gauche 3 conformer of 1,5-hexadiene was generated by setting the job type to energy, adding the additional key words pop=full and by selecting full NBO tab. The HF/3-21G method and basis set was still used in this calculation. The following MOs were generated.

In the HOMO of the gauche 3 conformer it can be seen that there are π-π interactions between the pi orbital of one alkene and the pi orbital of the other alkene in 1,5-hexadiene. These interactions are stabilising and do not occur in the app conformer and hence this one of the reasons why the gauche conformer is lower in energy than the anti conformer. The LUMO shows that in the gauche 3 conformer, there are steroelectronic effects, which stabilise the molecule. The molecule experiences hyper-conjugation because the σ orbitals of the C-C bond adjacent to a C=C bond, interact with the π^* orbitals of the alkene group. This interaction is also stabilising and hence another reason why the gauche conformer is lower in energy than the anti conformer.

Part D

The conformers have been compared with the conformers shown in Appendix 1 and the anti 1, gauche 1 and gauche 3 conformations have been produced from the optimisations carried out (see above).

Part E and F

The anti 2 conformation shown in Appendix 1 was drawn in Gaussview for this part of the investigation and then optimised by using the HF/3-21G method and basis set. The calculation took one minute to run. The point group of this conformer was found to be C_i and the results obtained are shown below. The optimised anti 2 conformer was then re-optimised by using a different method and basis set (DFT-B3LYP/6-31G(d)). The point group obtained remained the same as above and the following results were obtained.

Anti 2 (HF/3-21G) Results Summary
Dihedral Angle/^o	180.0
Charge	0
Spin	Singlet
Final Energy/a.u.	-231.69254
RMS Gradient/a.u.	0.000020
Dipole Moment/D	0.0015
Point Group	C_i

Anti 2 (DFT-B3LYP/6-31G(d)) Results Summary
Dihedral Angle/^o	180.0
Charge	0
Spin	Singlet
Final Energy/a.u.	-234.6117
RMS Gradient/a.u.	0.000013
Dipole Moment/D	0
Point Group	C_i

The energy values obtained for the anti 2 conformer have changed when using a different basis set and method. The energy value obtained whilst using DFT-B3LYP/6-31G(d) is lower than the energy value obtained when using the HF/3-21G. The values cannot be compared as different methods and basis sets yield different values because the approximations and calculations are different. The dihedral angles obtained from both methods were exactly the same. The bond lengths and bond angles of the anti 2 conformer using the DFT method were slightly different to the values obtained from the conformer optimised by the HF method (see table below). However, overall the anti 2 conformer obtained by each method had the same geometry. The table below shows that both methods and basis sets generate the anti 2 conformer, which has bond lengths and angles close to the literature values. However, it is known that the DFT-B3LYP/6-31G(d) method and basis set are more accurate and thus better to use.

	Literature Value^[1]	HF/3-21G	DFT-B3LYP/6-31G(d)
C=C Bond Length/Å	1.340	1.316	1.334
CH₂-CH Bond Length/Å	1.508	1.509	1.504
CH₂-CH₂ Bond Length/Å	1.538	1.553	1.548
CH₂-CH₂-CH Bond Angle/^o	111.5	111.3	112.7
CH₂-CH=CH₂ Bond Angle/^o	124.5	124.8	125.3

Part G

The DFT-B3LYP/6-31G optimised anti 2 conformer was opened in Gaussview and a frequency analysis was carried out on the conformer. The method and basis set remained unchanged, but the job type was changed to frequency. From the .log file obtained from the frequency calculation, the vibrations and IR spectrum of the anti 2 conformer were recorded. In addition, under the thermochemistry title in the .log file the following energies were found.

 Sum of electronic and zero-point Energies           = -234.469212 a.u.
 Sum of electronic and thermal Energies              = -234.461856 a.u.
 Sum of electronic and thermal Enthalpies            = -234.460912 a.u.
 Sum of electronic and thermal Free Energies         = -234.500822 a.u.

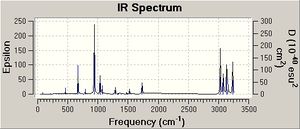
The vibrational frequencies obtained were all positive, which indicates that the anti 2 conformer obtained is the optimised structure. Negative frequencies are only obtained if the structure under consideration is not optimised. A single negative frequency indicates that the molecule obtained is a transition state, this is seen in the below investigations. 25 vibrational frequencies obtained from the above calculation on the anti 2 conformer had zero intensity and thus do not appear in the IR spectrum obtained. This is because these vibrational frequencies are IR inactive, as no change in dipole moment occurs during the vibration. Some frequencies obtained are low in value and these frequencies are due to vibrations of the centre of mass of the molecule and not vibrations of the bonds in the molecule.

Description of Vibration	Frequency/cm^-1	Intensity
C-H Stretch.	3080	36
C=C Stretch	1734	18
C-H Scissoring	1523	6
C-H bending	1289	6

Optimising the Chair and Boat Transition State Structures

The aim of this part of the investigation is to optimise both the chair and boat transition state structures, that occur during the Cope rearrangement of 1,5-hexadiene. Three different methods will be used to optimise the transition state structures: i) by computing the force constants; ii) using the redundant coordinate editor; iii) by using the QST2 method. From the optimised transition state structures, the reaction coordinate can be visualised and an IRC can be run on these structures. In addition, the activation energies for the Cope rearrangement via a chair and boat transition state can be determined.

Part A, B, C and D

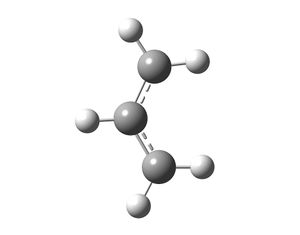
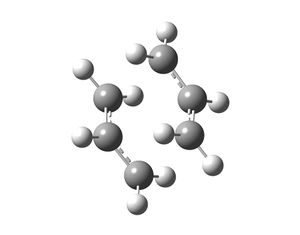
The allyl fragment (CH₂CHCH₂) was drawn in Gaussview and optimised using HF/3-21G as the method and basis set. The energy of this fragment was -115.8230 a.u. and the fragment had C_2v symmetry. Then a guess structure was constructed for the chair transition state. This was done by copying the optimised allyl fragment twice into a new window and arranging the fragments in such a way that the distance between the fragments was approximately 2.2Å.

This guess chair transition state structure was optimised and a frequency analysis was also carried out. This was done by selecting the job type Opt+Freq. The optimisation to a TS (Berny) was also selected and the HF/3-21G method and basis set were used. The additional key words opt=noeigen were also included in the input file. This calculation took 33 seconds. This method used to optimise the transition state is the force constant method, as the calculation was set to calculate the force constants once.

The guess chair transition state was then optimised again, but by using a different method compared to above (part c and d). This second method, first involved the bonds between the two allyl fragments of the guess chair transition state structure to be selected using the redundant coordinate editor. These bond coordinates were set to 2.2Å and the freeze coordinate option was selected. This structure was then optimised using HF/3-21G and the additional key words opt=modredundant.

Once this calculation was completed, the .chk file was opened and the resulting molecule was modified by using the redundant coordinate editor again. This time bonds previously selected were selected again, which were shown to be 2.2Å long and the derivative option was selected, instead of the freeze coordinate option. The modified molecule was re-optimised by using HF/3-21G and this calculation ran for one minute and 21 seconds. After the chair transition state had been optimised by the redundant coordinate method, the molecule was subjected to a frequency calculation. This was done by changing job type from optimisation to frequency and the HF/3-21G method and basis set was used. The following results were obtained from both optimisations of the chair transition state.

	Force Constant Method	Redundant Coordinate Method
C-C Bond Length within Allyl Fragment of Chair/Å	1.39	1.39
C-C Bond Length between Allyl Fragments in Chair/Å	2.02	2.02
Bond Angle within Allyl Fragment of Chair/^o	120.5	120.5
Energy/a.u.	-231.61932	-231.69132
Spin	Singlet	Singlet
Charge	0	0
RMS Gradient/a.u.	0.000017	0.000029
Dipole/D	0.0001	0.0001
Point Group	C_2h	C_2h
Imaginary Vibrational Frequency/cm^-1	-818.0	-817.8

The different methods used to optimise the chair transition state structure produced very similar results (see table above). Optimising transition state structures are very difficult as the reaction coordinate has to be known. The first method used to optimise the chair transition state structure used force constants. This method can only be used if the initial guess of the transition state is fairly good. If the transition state guessed is far from the actual structure then the force constant method cannot be used and hence the reaction coordinate editor is preferred method. This is because the inter-fragment bonds are frozen and the structure is optimised. When the structure is fully relaxed the bond coordinates are un-frozen and the transition state is optimised. This method has one advantage, which is that once the molecule has been relaxed it is not necessary to compute the whole Hessian, as differentiating along the reaction coordinate tends to be sufficient to yield a good result and hence computing time is minimised.

The frequency analysis on both optimised transition state structures were carried out and both yielded one negative frequency. This corresponds to the bond breaking and making that occurs during the Cope reaction. As one negative frequency is obtained, this proves that the transition state structure has been produced.

Part E

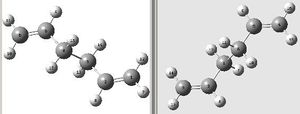
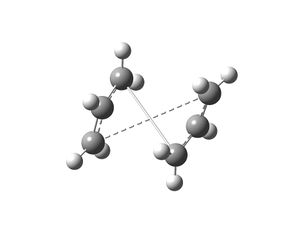
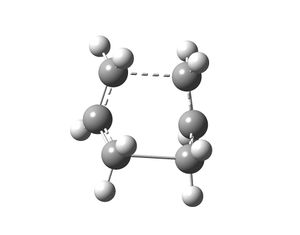
The boat transition state was optimised using a different method (QST2). This method looks at the reactant and product molecules in the Cope rearrangement and the calculation interpolates between the two structures to give the transition state. The anti 2 conformer of the 1,5-hexadiene produced in the previous section was copied into a new Gaussview window and a molgroup was added and the conformer was also copied in this other window. The two anti 2 conformers were labelled as shown on the left and these structures were submitted to be optimised. The job type selected was Opt+Freq and the TS(QST2) option was chosen and the HF/3-21G method and basis set were used. This job failed and yielded the structure on the right. The structure obtained is incorrect due to the fact that the calculation linearly interpolated between the reactant and product and did not consider rotation around the central bond.

The reactant and product molecules submitted to Gaussian to produce the boat transition state structure were modified by changing the central dihedral angle to 0^o and changing the inside C-C-C angle to 100^o. The resulting structures submitted to Gaussian are shown on the right. The same parameters were set as the first calculation and this calculation managed to work and the following results were recorded.

C-C Bond Length within Allyl Fragment of Chair/Å	1.38
C-C Bond Length between Allyl Fragments in Chair/Å	2.14
Bond Angle within Allyl Fragment of Chair/^o	121.7
Energy/a.u.	-231.60280
Spin	Singlet
Charge	0
RMS Gradient/a.u.	0.000020
Dipole/D	0.16
Point Group	C_2v
Imaginary Vibrational Frequency/cm^-1	-840.0

The frequency analysis only produced one negative frequency and hence clarified that the transition state had been obtained. The frequency corresponds to the bond breaking and making that occurs during the Cope rearrangement. The frequency is shown on the right. The energy value obtained for the boat transition state structure is higher in energy than the energy obtained for the chair transition state, which indicates that the energy barrier of the Cope rearrangement going via a boat transition state is bigger than the energy barrier that accompanies the Cope rearrangement which goes via a chair transition state. The boat transition state is higher in energy because it experiences more steric strain than the chair transition state.

Part F

The chair transition state looks like the gauche 2 conformer of 1,5-hexadiene and the boat transition state looks like the gauche 3 conformer of 1,5-hexadiene. However, it is hard to definitively predict the conformer that will be generated from a particular transition state. The Intrinsic Reaction Coordinate calculation is used to follow the minimum energy path from the transition state to the minimum on the potential energy surface, which thus allows the conformer of 1,5-hexadiene connected to a particular transition state to be deduced.

The IRC calculation was run on both the chair and boat transition states yielded from the previous exercises. This was done by carrying out a Gaussian calculation. The job type selected was IRC and the reaction coordinate was set to be computed in the forward direction only. The force constants were set to only be calculated once and thus only at the beginning. In addition, the IRC max was not specified and the number of points along the IRC was set to 50. Note the HF/3-21G method and basis set are still used.

Generally after this calculation the geometry produced has not yet reached a minimum and thus three other calculations can be carried out to obtain the minimum:

Select the last structure obtained from the IRC and perform an optimisation on the structure (using Opt to a minimum and HF/3-21G)
Carry out another IRC calculation, but set the number of points to 150
Re-calculate the IRC but compute the force constants at every step.

The last method is the most accurate but also the most expensive. All three methods were carried out in this investigation and the following results were obtained.

	Chair	Boat
IRC Result Using 50 Points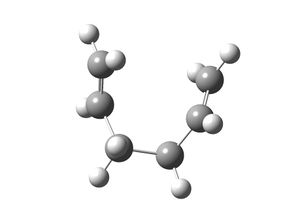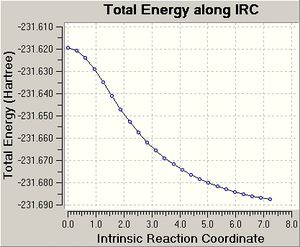
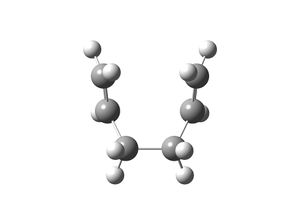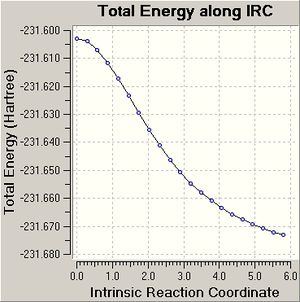Last Structure of IRC Optimised to a Minimum
IRC Result Using 150 Points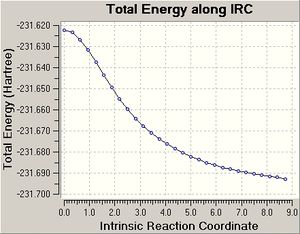
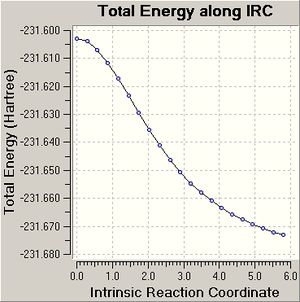IRC Computing Force Constants at each Step

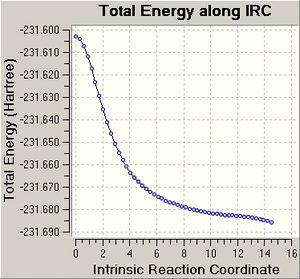For the chair, the IRC (50 points) calculation did not generate a minimum structure after 24 steps, which is conveyed by the graph produced, as the graph does not plateau. The conformer of 1,5-hexadiene produced after the last structure of the IRC was optimised to a minima is gauche 2. The energy and point group matched the values stated in appendix 1 and the conformer generated was the one expected.

The IRC (150 points) calculation on the chair transition state finished after 29 steps and did not reach a minimum as the graph produced does not plateau. The IRC calculation of the chair transition state, which computes force constants at every step finished after 46 steps and does generate a minimum structure as a plateau is reached. The energy of the conformer of 1,5-hexadiene produced is -231.69513, which does not match any of the energies of the conformers in appendix 1. Therefore the chair transition state seems to lead to a different conformer of 1,5-hexadiene. The point group of the conformer produced from the force constant IRC was C₂, which is the same point group of the gauche 2 conformer, which is what was expected to be generated from IRC calculation on the chair transition state.

For the boat transition state, the IRC 50 and IRC 150 calculations did not reach a minimum structure as the graphs produced did not plateau. Both IRC calculations were completed in 21 steps. The last structure generated by the IRC 50 calculation was optimised to a minimum and the conformer generated (see above) was the gauche 3 conformer, which was expected because by inspection of the boat transition state, it seems that the boat resembles the gauche 3 conformer.

The IRC calculation that computes force constants at each point finished after 41 steps and produced a graph that plateaus and thus the conformer generated is a minimum structure. This conformer does not match in energy with any of the conformers in appendix 1, but the point group matches the point group of gauche 3, which was the expected conformer to be produced from the IRC calculation of the boat transition state.

The optimisation of the final IRC structure to a minimum produced results that were expected, but the IRC method which computes the force constants at each step does not give the conformers expected to be generated from the chair and boat transition states. The latter method is more accurate and hence it could be true that the chair and boat transition state structures generated new conformers of 1,5-hexadiene and not gauche 2 and gauche 3, which were suggested by inspection of the transition state structures.

Part G

The Chair and Boat transition state structures obtained by using the HF/3-21G were subjected to another optimisation and frequency calculation which used the DFT-B3LYP/6-31G(d) method and basis set. The following results were obtained.

	Chair HF/3-21G	Chair DFT-B3LYP/6-21G(d)	Boat HF/3-21G	Boat DFT-B3LYP/6-21G(d)
C-C Bond Length within Allyl Fragment of Chair/Å	1.39	1.40	1.38	1.39
C-C Bond Length between Allyl Fragments in Chair/Å	2.02	1.97	2.14	2.20
Bond Angle within Allyl Fragment of Chair/^o	120.5	120.0	121.7	122.3

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy/a.u.	Sum of electronic and zero-point energies/a.u.	Sum of electronic and thermal energies/a.u.	Electronic energy/a.u.	Sum of electronic and zero-point energies/a.u.	Sum of electronic and thermal energies/a.u.
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461340	-234.556982	-234.414934	-234.409014
Boat TS	-231.602802	-231.450930	-231.445302	-234.543076	-234.402315	-234.395995
Anti 2 Conformer	-231.692535	-231.539539	-231.532564	-234.611702	-234.469212	-234.461856

To work out the activation energies at 0K, the sum of the electronic and zero point energies obtained for the anti 2 conformer was subtracted from the sum of the electronic and zero point energies of the transition state structure. The value was then multiplied by 627.509 to convert the values into kcal/mol. The activation energies at 298K were found by using the sum of the electronic and thermal energies instead of the sum of the electronic and zero point energies.

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)/kcalmol^-1	45.71	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat)/kcalmol^-1	55.60	54.76	41.98	41.33	44.7 ± 2.0

Looking at the results produced from both methods, the geometries of the anti 2 conformer, chair and boat transition states (see part e and f in previous section and table above) are similar but the energy differences are fairly different and hence when carrying out an investigation in order to map the potential energy surface, a low level calculation should be carried out first and then the structure should be re-optimised using a high level theory calculation. The energy values obtained are very close to the values reported in the results table on the wiki page Mod:phys3. This is expected because the calculations were run with the same methods and the structures used were exactly the same. The reason for the very small discrepancies is that there is some error on the values calculated by Gaussian and thus each calculation with the same method may vary very slightly.

Diels-Alder Cycloaddition

A Diels-Alder reaction is classed as a pericyclic reaction between a diene and a dieneophile. A pericyclic reaction is known to have cyclic transition structures in which all bond forming and breaking reactions occur in a concerted fashion, without any intermediates forming.^[2]

The π orbitals of the dieneophile interact with the π orbitals of the diene to form σ bonds. The number of π electrons determines whether the reaction is concerted or not. However, generally a pericyclic reaction is concerted.

Diels-Alder Reaction between Cis-butadiene and Ethene

During a Diels-Alder reaction, the HOMO or LUMO of one reactant interacts with the HOMO or LUMO of the other reactant to form two new bonding and anti-bonding MOs. The reaction is concerted and thus allowed if the HOMO of a reactant has the same symmetry as the LUMO of the other reactant and thus the HOMO and LUMO can interact. If this interaction does not occur due to the symmetry of the HOMO and LUMO not being the same, then the reaction is stepwise and forbidden.

If the dieneophile has substituents on it that have π orbitals, which can interact with the new double bond that is forms in the Diels-Alder reaction then this can stabilise the product and determine the regiochemistry of the reaction.

In this investigation the Diels-Alder reaction between cis-butadiene and ethylene is being considered. The ethylene approaches the cis-butadiene from above. The π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene interact to form the product. This is a [4s + 2s] cycloaddition because the butadiene has 4 π orbitals and the ethylene has 2 π orbitals that are involved in the reaction.

Part i)

Cis-butadiene and ethylene were drawn in Gaussview and optimised by using the HF/3-21G method and basis set. Then these structures were re-optimised by using the semi-empirical AM1 method. The latter method allows the MOs of both reactants to be analysed.

	cis-butadiene	ethene
Optimised Structure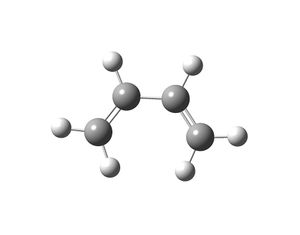
HOMO
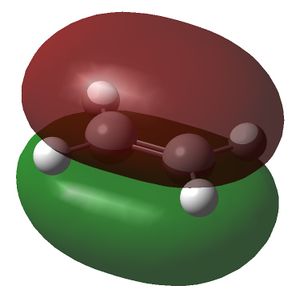Symmetry of HOMO	a	s
LUMO
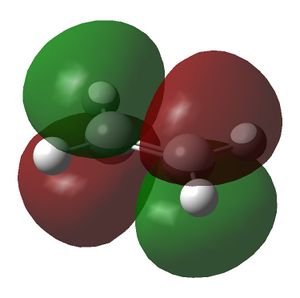Symmetry of LUMO	s	a

The symmetry of the MOs in the above table were deduced with respect to the σ_v plane. The HOMO of the cis-butadiene and the LUMO of the ethene can interact during the Diels-Alder reaction and the LUMO of the cis-butadiene can interact with the HOMO of the ethene. This is because interactions between MOs can only occur if they have the same symmetry. Therefore the HOMOs cannot interact with one and other and neither can the LUMOs. In the optimised structure of cis-butadiene the C=C bond length is 1.335Å, the C-C bond length is 1.449Å, the C-C=C bond angle is 125.7^o and the dihedral angle of the molecule is 0.132^o. The C=C bond length in the optimised ethene structure is 1.326Å.

Part ii)

The transition state structure of the Diels Alder reaction between cis-butadiene and ethene has an envelope structure because this shape maximises the overlap between the pi orbitals of the butadiene and ethene. The transition state structure was drawn in Gaussview and the distance between the two fragments of the transition state was guessed to be 2.0Å. This distance was chosen because the inter-fragment bonds will be longer than 'normal' single bonds, which are roughly 1.54Å long.

This structure was then optimised by using the HF/3-21G method and basis set. The job type used was Opt+Freq; the force constants were set to be calculated always; the additional key words opt=noeigen were used and the optimisation to TS(Berny) was selected. The structure obtained was then used to obtain the HOMO and LUMO of the transition state. This was done by using the semi-empirical AM1 method. The following results were obtained. The redundant coordinate method was not used to optimise the transition state because the structure drawn was a good guess for the actual transition state structure and hence worked. If the force constant method did not work then the redundant coordinate method would have been used. The reason why the force constant method was used in the first place was because it is easier.

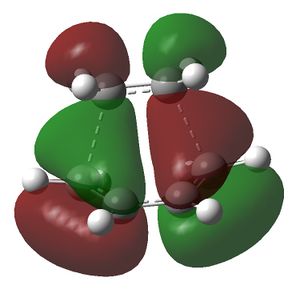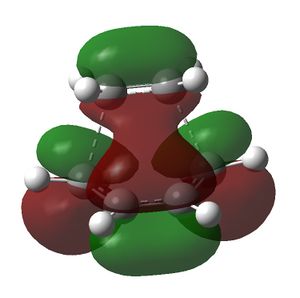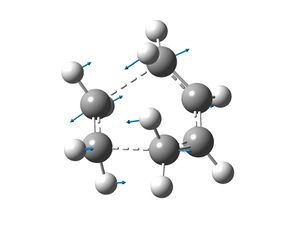The two new sigma bonds that begin to form between the cis-butadiene and ethene fragments in the transition state structure were 2.119Å long. This is longer than a ‘normal’ C-C single bond, which is expected because the sigma bonds that form in the Diels-Alder reaction are only partially formed in the transition state. The C=C double bonds of the cis-butadiene part of the transition state were 1.382Å long and are no longer shown as double bonds but as a one full bond and a partial bond. This bond length has increased compared to the bond length in the cis-butadiene reactant (see above). The reason for this is that the double bond changes to a single bond in the product. Single C-C bonds are longer than a C=C double bond and hence the bond length increases in the transition state as the C=C bond starts to form a single bond. The C-C bond length of the cis-butadiene part of the transition state is 1.398Å and this has decreased compared to the C-C bond length in the cis-butadiene reactant (see above). This is expected because this bond transforms into a C=C bond in the product which is smaller than a C-C single bond. The C=C of the ethene part of the transition state is 1.383Å long, which is longer than the bond length recorded for the ethene reactant (see above). This is because the C=C bond of ethene changes to a single C-C bond in the product, which is longer than a C=C bond.

In the transition state the bonds have started to form and break and thus the bonds that are changing from sp² to sp³ character are lengthening. The bonds which are going from sp³ to sp² are shortening in length. The bond length for a 'normal' C=C bond is 1.32Å and for a C-C bond the length is 1.54Å.^[3]

The HOMO of the transition state structure is antisymmetric and the LUMO is symmetric. The HOMO of the transition state is generated by the interaction between the HOMO of the cis-butadiene and the LUMO of the ethene, which are both antisymmetric. The LUMO of the transition state is produced from the HOMO of the ethene and the LUMO of the cis-butadiene, which are both symmetric. As the interacting MOs have the same symmetry the reaction is allowed.

The frequency analysis of the transition state yielded a negative frequency at -956cm^-1. This single frequency indicates that the transition state has been found and this vibration corresponds to the reaction path and indicates that the bond formation of the two new sigma bonds is synchronous (the reaction is concerted). The lowest positive frequency at 147cm^-1 conveys asynchronous sigma bond formation.

Part iii)

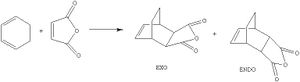
Cyclohexa-1,3-diene undergoes a Diels-Alder reaction with maleic anhydride. The endo product is the major product and the reaction is controlled kinetically and thus the transition state which leads to the formation of the exo product must be higher in energy. Two transition state structures were drawn in Gaussview, one yields the endo prodcut and the other produces the exo product. The geometry of the transition state structures were optimised by selecting opt+freq, the HF/3-21G method and basis set, TS(Berny), calculate force constants always and adding the key words opt=noeigen. Once the transition state structures were optimised, a semi-empirical AM1 calculation was run on them to generate the MOs for each transition state.

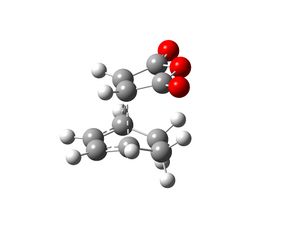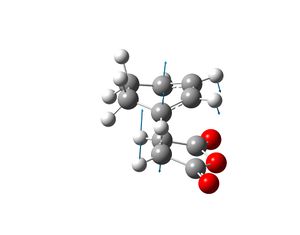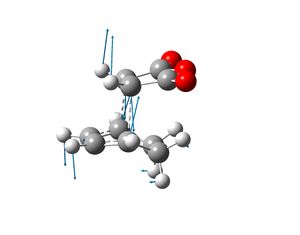The energy of the endo transition state was found to be -0.51505 a.u. and for the exo transition state the energy was -0.050420 a.u. and thus the endo transition state is lower in energy. This is expected because the exo transition state has more steric hindrance present due to the clash between the 3 oxygen atoms of the maleic anhydride and the bridging carbons. The steric clash can also be seen in the geometry of the endo and exo transition states. The two new sigma bonds that start to form in the transition state have a bond length of 2.16Å in the endo transition state and the bond length in the exo transition state is 2.17Å. The bonds are longer in the exo transition state because the steric clash between the maleic anhydride and the bridging carbons prevents the inter-framents to get closer together and thus the bonds becomes longer compared to the bonds in the endo transition state.

The exo transition state is more strained due to steric repulsions experienced between the O atoms of the maleic anhydride fragment and the C-H bridge bonds. The endo transition state has steric repulsions between the O atom of maleic anhydride and the H atoms of the cyclohexa-1,3-diene, but the through space distance between the O and the H atoms is 3.46Å in the endo product and in the exo product it is 2.76Å and thus due to the O and H atom being closer in the exo transition state, the repulsions experienced by the exo transition state is much greater and thus destabilising.

For both the exo and endo transition states the C-C bond lengths of the cyclohexa-1,3-diene fragment that are involved in the Diels-Alder reaction (i.e. the bonds being formed and broken) are 1.39Å long. The double bond in the maleic anhydride fragment of the transition state is 1.41Å long. This shows that in both transition states the double bond of the maleic anhydride is no longer of double bond character as it is longer than a ‘normal’ double bond. This is expected because the double changes to a single bond during the reaction. The double bonds in the cyclohexadiene fragment of the transition states are longer than 'normal' C=C bonds, which is expected as these bonds convert to single bonds, which are longer than double bonds. In the transition states, these changes has already started to occur and hence the bonds have lengthened. The single bond in the cyclohexadiene fragment of the transition states is shorter than the average single bond (1.54Å), which is due to the fact that this bond has started to form a double bond.

The frequency analysis of both transition states produced a negative frequency, which proves that the transition state has been obtained. The negative frequency also portrays the bond formation of the two new sigma bonds and conveys that the reaction is a concerted process. The imaginary frequency for the endo transition state was at -806cm^-1 and for the exo transition state, the imaginary frequency was at -812cm^-1.

	Cyclohexa-1,3-diene	Maleic Anhydride	Endo TS	Exo TS
HOMO
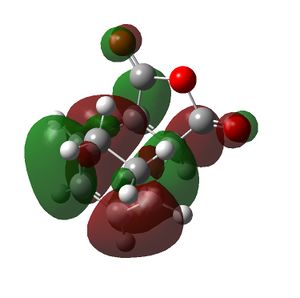Symmetry of HOMO	a	s	a	a
LUMO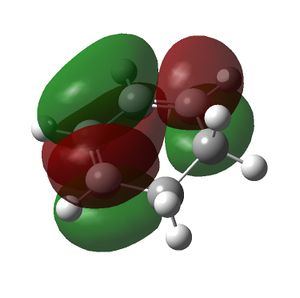
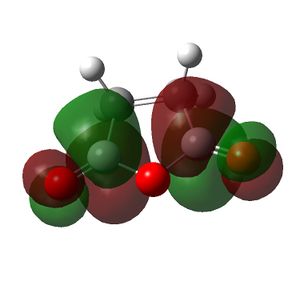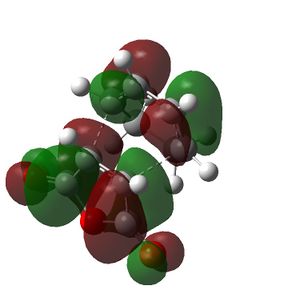Symmetry of LUMO	s	a	a	a

The HOMO of the cyclohexa-1,3-diene and the LUMO of the maleic anhydride interact to produce the HOMO of the transition states. The exo transition state is less stable than the endo transition state due to steric reasons, which were discussed above and shown by the bond lengths in both transition states. However, the endo product is also more stable due to secondary orbital overlap effects, which are stabilising. The CH=CH pi orbitals of the cyclohexa-1,3-diene fragment in the HOMO of the endo transition state can overlap with the π^* orbitals of the O=C groups of the maleic anhydride fragment of the endo transition state. This is because the π^* orbitals of the O=C groups have nodes in the plane of the maleic anhydride molecule. These orbitals can overlap and interact with the pi orbitals of the conjugated part of the cyclohexa-1,3-diene fragment of the endo transition state. This orbital overlap can only occur in the endo transition state because the O=C-O-C=O fragment is beneath the conjugated part of the cyclohexa-1,3-diene ring. In the exo transition state the O=C-O-C=O fragment is beneath the bridge (non-conjugated) part of the cyclohexa-1,3-diene ring and thus cannot undergo this secondary orbital overlap. This overlap in the endo transition state is stabilising and thus lowers the energy of the endo transition state.^[4]

This secondary orbital overlap is not shown in the HOMO produced for the endo transition state as the π^* orbitals of the O=C-O-C=O fragment do not blend with the CH=CH π orbitals. This is seen because there is no electron density between the carbonyl carbon atom of the maleic anhydride fragment and the CH=CH of the cyclohexadiene fragment. This could mean that the secondary orbital overlap does not occur in the endo product and hence the reason for the difference in energy between the exo and endo transition states is due to steric reasons only. The other conclusion is that the secondary orbital overlap is not seen in the calculated MOs because the calculations are approximations and the basis set used is not very accurate and thus the secondary orbital overlap may not have been produced. If a better and higher level method and basis set is used these effects may be seen, as the accuracy of the calculation will be higher.

The presence of substituents on the diene and dieneophile affect the rate of the Diels-Alder reaction. If the substituent on the diene is electron donating and the group on the dieneophile is electron withdrawing the rate of the Diels-Alder reaction will increase. This is because the energy of the HOMO of the diene increases if an electron donating group is present on the diene and the energy of the LUMO of the dieneophile decreases if an electron withdrawing group is present. This therefore brings the interacting orbitals closer together in energy and thus the orbitals will interact more strongly and the energy of the transition state will be lower than the transition of the molecules without the substituents.^[5]

The maleic anhydride has three O atoms which are strongly electron withdrawing and hence the reaction of cyclohexadiene with maleic anhydride will be much faster than the reaction of cyclohexadiene with cyclopentene.

Extra

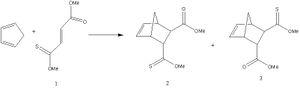
Another Diels-Alder cycloaddition occurs between cyclopentadiene and molecule 1 (see left). This reaction yields two products (2 and 3). The ratio of the products 2 and 3 produced is 7:3. This indicates that the endo-thioester is the major product compared to the endo-ester product. Both the thioester and ester have endo directing abilities but the former is more superior. The reaction was reported in the literature to have been carried out at room temperature and thus under kinetic control and hence product 2 must be the kinetic product. The solvent was varied (CDCl₃ and DMSO were used as solvents) and the ratio of the products remained the same and thus the stereo and regiochemistry of the reaction is not influenced by solvents. The literature also reported the ratio of the products formed when Lewis acids were added to the reaction. The Lewis acids were seen to influence the ratio of the products produced. Some Lewis acids increased the amount of product 2 produced and some increased the amount of product 3 produced.^[6]

The transition states which produce molecules 2 and 3 were drawn in Gaussview and optimised. This was done by selecting Opt+Freq, TS(Berny), always calculate force constants, HF/3-21G and adding the words opt=noeigen. Once the structures were optimised the transition states were subjected to another optimisation using the semi-empirical AM1 method. The following structures and imaginary frequencies were obtained.

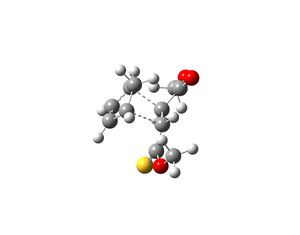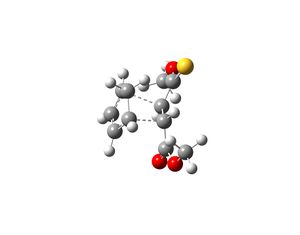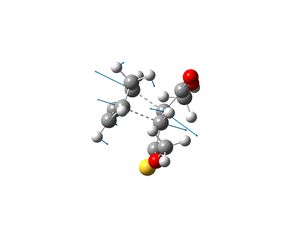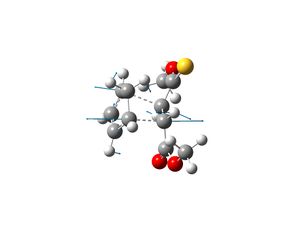Both transition state structures produced one imaginary frequency, which proves that the molecules obtained are transition states. The imaginary frequency of the transition state which produces molecule 2 is -753cm^-1 and the negative frequency of the other transition state which produces molecule 3 is -758cm^-1. The vibrations that correspond to these frequencies are shown above and they show that the bond formation of the two new sigma bonds is synchronous and thus the Diels-Alder reaction is concerted. This therefore indicates that the interaction between the HOMO of cyclopentadiene and LUMO of molecule 1 is allowed, as they must have the same symmetry in order for the reaction to be concerted.

The interfragment bond lengths (bond lengths of the two new sigma bonds that are form in the transition states) are very similar. The bond length of the transition state that yields molecule 2 is 2.25Å and for the other transition state the bond length is 2.23Å. The energy of the transition state that produces molecule 2 is -0.015945 a.u. and for the other transition state the energy is -0.015869 a.u. The results shown that the transition state for molecule 2 is lower in energy and thus molecule 2 is the kinetic product. This is expected as the reactions occurred under room temperature (see literature) and thus as the reaction conditions are mild, the reaction was assumed to be under kinetic control and hence the major product is the kinetic product. The results from computational analysis have confirmed this theory.

References

↑ G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, 63-69. DOI:10.1016/0022-2860(94)09007-C
↑ Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.2.
↑ L. Bartell, J. Am. Chem. Soc., 1959, 81 (14), pp 3497–3498. DOI:10.1021/ja01523a002
↑ Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.48.
↑ Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.49.
↑ C. Braddock, J. Brown, J. Chem. Soc., Chem. Commun., 1993, 1244-246. DOI:10.1039/C39930001244

Data Files

Boat Transition State QST2 Optimisation DOI:10042/to-4209
Boat Transition State DFT Optimisation DOI:10042/to-4210
Chair Transition State DFT Optimisation DOI:10042/to-4211
Boat Transition State DFT Frequency DOI:10042/to-4212
Chair Transition State DFT Frequency DOI:10042/to-4213
Chair Transition State Force Constant IRC DOI:10042/to-4214
Chair Transition State IRC 150 DOI:10042/to-4215
Boat Transition State IRC 50 DOI:10042/to-4216
Boat Transition State IRC 150 DOI:10042/to-4217
Boat Transition State Force Constant IRC DOI:10042/to-4218
Diels Alder Transition State Opt DOI:10042/to-4219
Cyclohexa-1,3-diene Opt DOI:10042/to-4220
Maleic Anhydride Opt DOI:10042/to-4221
Exo Transition State AM1 Opt DOI:10042/to-4222
Endo Transition State AM1 Opt DOI:10042/to-4223
Molecule 2 Transition State AM1 Opt DOI:10042/to-4224
Molecule 3 Transition State AM1 Opt DOI:10042/to-4225

[1] G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, 63-69. DOI:10.1016/0022-2860(94)09007-C

[2] Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.2.

[3] L. Bartell, J. Am. Chem. Soc., 1959, 81 (14), pp 3497–3498. DOI:10.1021/ja01523a002

[4] Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.48.

[5] Ian Fleming, Pericyclic Reactions,Oxford University Press, 2008, pp.49.

[6] C. Braddock, J. Brown, J. Chem. Soc., Chem. Commun., 1993, 1244-246. DOI:10.1039/C39930001244

[1]

[2]

[3]

[4]

[5]

[6]