Rep:Mod:physcompquintinlo00690346
Module 3: Transition States and reactivity
Introduction
Computational chemistry use simulations to solve complex chemical problems. It helps us to visualise the correlations between the properties and structure of compounds and to simulate chemical reactions without having to carry out the actual experiment in the laboratory. There are numerous methods available in computational chemistry, they range from ab-initio methods such as Hartree-Fock(HF) and Density Functional theory (DFT) to empirical and semi-empirical methods such as Austin Model 1(AM1). We will use these methods to characterise transition structures on potential energy surfaces for the Cope rearrangement and Diels-Alder cycloaddition reactions in this experiment.
The Cope Rearrangement Tutorial
The Cope rearrangement of 1,5-hexadiene was analysed using Gaussview 5.0.9. The purpose of this tutorial is to obtain a low-energy minima, the transition state structures of 1,5-hexadiene potential energy surface and the preferred mechanistic pathway of the reaction. Gaussview 5.0.9 allows us to calculate both the activation energy and enthalpy of this rearrangement.
Optimisation of the reactants and products
Anti Conformation
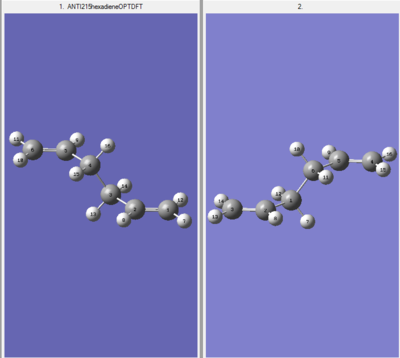
A 1,5-hexadiene structure with an "anti" linkage for the 4 central carbon atoms was drawn using Gaussview 5.0.9. This structure was then optimised using HF/3-21G level of theory where the calculation method was Hartree-Fock and the basis set was 3-21G. The .log file can be found here File:Qlo15hexadieneANTIOPT.chk.

| File Name | qlo15hexadieneANTIOPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69260 au |
| RMS GRADIENT NORM | 0.00001297 au |
| Imaginary Freq | |
| Dipole Moment | 0.20 Debye |
| Point Group | C2 |
A point group of C2 was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure is also known as the anti1 conformer of 1,5-hexadiene.
Gauche Conformation
A 1,5-hexadiene structure with a "gauche" linkage was drawn using Gaussview 5.0.9. The gauche conformation was expected to be slightly higher in energy than the anti conformation, which was not the case when the energy of the optimised gauche structure was obtained in Gaussview (shown in table 2 below). It was reported in Gung et. al.[1] that unlike n-butane, where the anti structure is more stable than the gauche structure, the gauche conformations are as stable or even more stable than its anti counterparts. This unusual phenomenon has direct implications in the reactivity of the Cope rearrangement which we will explore further later. The .chk file for the optimisation of this gauche structure can be found here File:Qlo15hexadieneGAUOPT.chk.

| File Name | qlo15hexadieneGAUOPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69266 au |
| RMS GRADIENT NORM | 0.00000769 au |
| Imaginary Freq | |
| Dipole Moment | 0.34 Debye |
| Point Group | C1 |
A C1 point group was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised gauche structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure is also known as the gauche3 conformer of 1,5-hexadiene.
Based on the results above and also from literature[1], the gauche conformation of 1,5-hexadiene should have the lowest energy. Several more gauche structures were optimised on Gaussview 5.0.9 tp see if this was true. The .chk file for this optimisation can be found here File:Qlo15hexadieneGAU1OPT.chk.

| File Name | qlo15hexadieneGAU1OPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.68772 au |
| RMS GRADIENT NORM | 0.00002601 au |
| Imaginary Freq | |
| Dipole Moment | 0.46 Debye |
| Point Group | C2 |
A C2 point group was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised gauche structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure shown in diagram 3 above is known as the gauche conformer of 1,5-hexadiene.
Another gauche conformation of 1,5-hexadiene was drawn and optimised using Gaussview 5.0.9 and the results obtained are shown below. The .chk file for this optimisation can be found here File:Qlo15hexadieneGAU2OPT.chk.

| File Name | qlo15hexadieneGAU2OPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69167 au |
| RMS GRADIENT NORM | 0.00001086 au |
| Imaginary Freq | |
| Dipole Moment | 0.38 Debye |
| Point Group | C2 |
A C2 point group was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised gauche structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure shown in diagram 4 above is the gauche2 conformer of 1,5-hexadiene.
One final gauche conformation of 1,5-hexadiene was drawn and optimised using Gaussview 5.0.9, the results for this optimisation is shown below. The .chk file for this optimisation can be found here File:Qlo15hexadieneGAU4OPT.chk.
| File Name | qlo15hexadieneGAU4OPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69153 au |
| RMS GRADIENT NORM | 0.00001866 au |
| Imaginary Freq | |
| Dipole Moment | 0.13 Debye |
| Point Group | C2 |
A C2 point group was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised gauche structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure is the gauche4 conformer of 1,5-hexadiene.
It was noted that the computed energies of all the optimised structures (anti and gauche) matches the energy values reported in Appendix 1.
It was found that overall, the energies of the gauche conformations of 1,5-hexadiene are as stable or more stable(as in the case of gauche3) than the anti1 conformation of 1,5-hexadiene. This matches literature[1],[2] descriptions.
The 3-21G basis set is a split valance basis set, where only the double zeta for the valance orbital electrons are calculated as the inner shell electrons are not as important to the calculations, it is a low level basis set which has rather low accuracy. Preferably a higher basis set such as 6-31G(d) should be used for these calculations, which was used by Gung et. al.[1] and Rocque et. al.[2] . This explains the discrepancies between the reported values in literature[1],[2] and the computed values shown in the tables above. The energy obtained for each optimisation is directly related to the basis set used.
anti2 conformation of 1,5-hexadiene
The Ci anti2 conformation of 1,5-hexadiene was drawn and optimised on Gaussview 5.0.9 using the HF/3-21G level of theory. The .chk file for this optimisation can be found here File:Qlo15hexadieneANTI2OPT.chk.
| File Name | qlo15hexadieneANTI2OPT |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69254 au |
| RMS GRADIENT NORM | 0.00001866 au |
| Imaginary Freq | |
| Dipole Moment | 0.00 Debye |
| Point Group | Ci |
A Ci point group was obtained after Symmetrize was selected under the edit menu. The energy and the point group of this optimised gauche structure was then compared with the conformers of 1,5-hexadiene shown in Appendix 1 and it was determined that this computed structure shown in diagram 6 above is the anti2 conformer of 1,5-hexadiene.
The point group and energy shown in table 6 above for the computed anti2 conformation of 1,5-hexadiene (-231.69254 au) is the same as the energy reported in appendix 1, where the anti2 conformation is slightly less stable than the anti1 conformation.
This anti2 conformation of 1,5-hexadiene was then optimised using the B3LYP/6-31G* level. The .chk file for this optimisation can be found here File:Qlo15hexadieneANTI2OPTDFT2.chk.
| File Name | qlo15hexadieneANTI2OPTDFT2 |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.61171 au |
| RMS GRADIENT NORM | 0.00003709 au |
| Imaginary Freq | |
| Dipole Moment | 0.00 Debye |
| Point Group | Ci |
6-31G* is known as a Pople's split-valance double-zeta basis set with added d polarisation for non-hydrogen atoms. The energy reported in table 7 is approximately 3 au lower than the energy reported in table 6, where a HF/3-21G level of theory was used. The difference in energy could be attributed to the higher level basis set used (6-31G*) when compared to 3-21G, which has a higher level of accuracy and it gives a better description of the core and valance electrons. The difference in energy can also be due to the use of electron density in B3LYP/6-31G* calculations as compared to the wave function used by HF/3-21G calculations.
Frequency analysis of the anti2 conformation of 1,5-hexadiene
Frequency analysis gives us the second derivative of a potential energy surface, where a minimum and a transition state on a potential energy surface can be differentiated. A minimum is present when there are no negative frequencies and the opposite is true for a transition state. This analysis allows us to generate an IR spectrum of the molecule, illustrating the different vibrational modes of the molecule.
The B3LYP/6-31G* anti2 1,5-hexadiene structure was subjected to frequency analysis on Gaussview 5.0.9. An infrared (IR) spectrum was computed as a result of this analysis, this spectrum is shown in diagram 8 below. The .log file for this frequency analysis can be found here File:QLO15HEXADIENEANTI2OPTDFT2.LOG.
| File Name | QLO15HEXADIENEANTI2FREQDFT2 |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.61171 au |
| RMS GRADIENT NORM | 0.00004508 au |
| Imaginary Freq | |
| Dipole Moment | 0.00 Debye |
| Point Group | Ci |
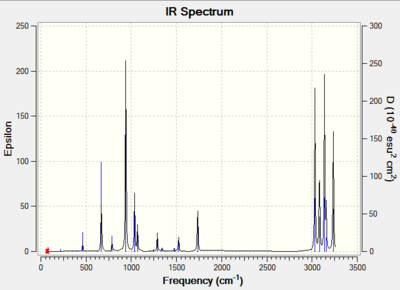

There are no imaginary(negative) frequencies present in this IR spectrum. Frequency analysis also allows us to obtain thermalchemical information of this molecule, such as the sum of electronic and zero-point energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies, and the sum of electronic and thermal free energies. These are shown in table 9 below.
| Energy (Hartrees/au) | |
|---|---|
| Sum of electronic and zero-point energies | -234.46921 |
| Sum of electronic and thermal energies | -234.46186 |
| Sum of electronic and thermal enthalpies | -234.46091 |
| Sum of electronic and thermal free energies | -234.50078 |
Optimising the "Chair" and "Boat" Transition Structures
In this section both the "Chair" and "Boat" transition structures were optimised by computing the force constants and using both the redundant coordinate editor and QST2.
Optimisation of the allyl fragment
An allyl fragment (CH2CHCH2) was first optimised using the HF/3-21G level of theory, the .log file for this optimisation can be found here. File:QLOHALFC2VBOATTSSTATEOPT.LOG.
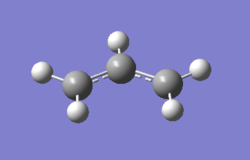
| File Name | qlohalfc2vboattsstateOPT |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | UHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(UHF) | -115.82304 au |
| RMS GRADIENT NORM | 0.00003049 au |
| Imaginary Freq | |
| Dipole Moment | 0.03 Debye |
| Point Group | C2V |
The allyl fragment was then optimised using B3LYP/6-31G* level of theory. The .log file for this optimisation can be found here File:QLOHALFC2VBOATTSSTATEOPTDFT.LOG.
| File Name | qlohalfc2vboattsstateOPTDFT |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | UB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Doublet |
| E(UB3LYP) | -117.26035 au |
| RMS GRADIENT NORM | 0.00009517 au |
| Imaginary Freq | |
| Dipole Moment | 0.08 Debye |
| Point Group | C2V |
Optimisation of the "Chair" transition state
After optimisation, this HF/3-21G optimised allyl fragment was then used to build up the "Chair" transition state, where the two fragments were approximately 2.2 Å apart. This transition state is an approximate structure and it was first optimised using HF/3-21G level of theory. The .log file for this optimisation can be found here File:QLOCHAIRTSGUESSOPTFREQ.LOG.
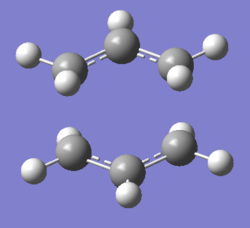
| File Name | qlochairtsguessOPTFREQ |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.619322 au |
| RMS GRADIENT NORM | 0.00002778 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.00 Debye |
| Point Group | C2h |
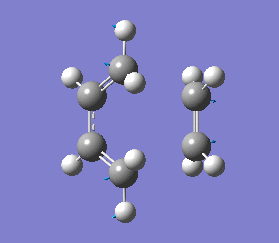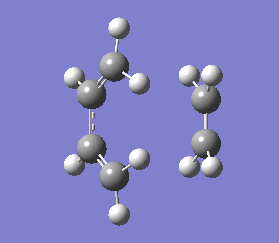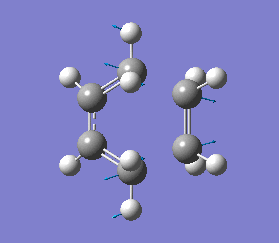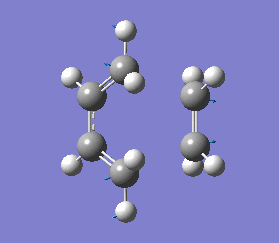
Frequency calculations gave an imaginary frequency at -817.93 cm-1, indicating the job has been completed successfully, as the presence of an imaginary frequency implies that a transition state is present. The vibration at this frequency corresponds to the Cope rearrangement as shown in diagram 11 below.

| Energy (Hartrees/au) | |
|---|---|
| Sum of electronic and zero-point energies | -231.46671 |
| Sum of electronic and thermal energies | -231.46135 |
The computed energies correlates well with the energies reported in appendix 2, indicating both the optimisation and frequency analysis were carried out correctly. These energy values will be used later in this report to calculate the activation energy of the Cope rearrangement reaction (section 2.2.6).
The B3LYP/6-31G* optimised allyl fragment mentioned earlier was then used to build up another "Chair" conformation, where the two fragments were approximately 2.2 Å apart. This transition state is an approximate structure and it was first optimised using B3LYP/6-31G* level of theory. The .log file for this optimisation can be found here File:QLOFULLSTRUCTUREOPTDFT.LOG.
| File Name | qlochairtsguessOPTFREQ |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.55700 au |
| RMS GRADIENT NORM | 0.00002935 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.00 Debye |
| Point Group | C2h |
The energy (-234.55700 au) for this B3LYP/6-31G* optimised "Chair" transition state is consistent with the energy reported in Appendix 2, thus indicating that the optimisation was carried out correctly. Frequency calculations gave an imaginary frequency at -565.48 cm-1, indicating the job was completed successfully. The vibration at this frequency corresponds to the Cope rearrangement as shown in diagram 12 below.
By comparing the HF/3-21G optimisation with the B3LYP/6-31G* optimisation of the "Chair" transition state, B3LYP/6-31G* optimisation gave a lower energy than HF/3-21G optimisation even though the structures for both transition states were almost identical. The difference in energy can be attributed to the slightly higher accuracy of the 6-31G* basis set, where the reasons were mentioned earlier in this report. 6-31G* has greater flexibility and more primitives which gives better and more accurate results and the B3LYP/6-31G* level of theory gives a better description of the core and valance electrons, which will result in a lower energy value. The difference in energy is also due to the electron density used by the DFT(B3LYP/6-31G*) method as compared to the wave functions used by HF/3-21G.
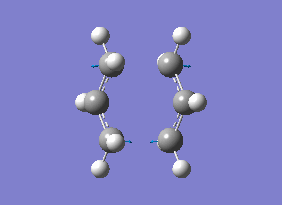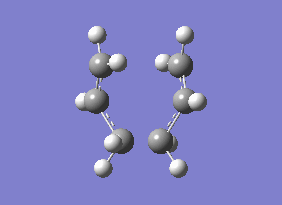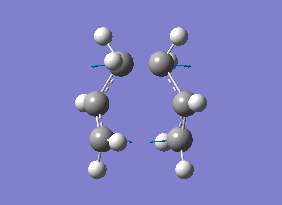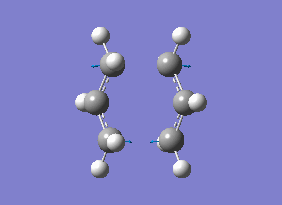
| Energy (Hartrees) | |
|---|---|
| Sum of electronic and zero-point energies | -234.41493 |
| Sum of electronic and thermal energies | -234.40901 |
The computed energies correlates well with the energies reported in appendix 2. These energy values will be used later in this report to calculate the activation energy of the Cope rearrangement reaction (section 2.2.6).
Frozen state optimisation of the "Chair transition state
The transition state structure was then optimised using the frozen state method, where all four terminal carbon atoms from the allyl fragments which form/break a bond during the rearrangement had their coordinates frozen and the optimisation was then carried out using HF/3-21G level of theory. The .chk file for this optimisation can be found here File:QlochairtsguessOPTFREQFROZEN.chk.
| File Name | qlochairtsguessOPTFREQFROZEN |
|---|---|
| File Type | .chk |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.56678 au |
| RMS GRADIENT NORM | 0.01218047 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.72 Debye |
| Point Group | C2h |
The transition state obtained here in diagram 13 looks very similar to the optimised transition state in diagram 10, which was expected. The bond forming/breaking distances was fixed at 2.2 Å and it was optimised again on Gaussview 5.0.9. The .log file for this optimisation is found here File:QLOCHAIRPARTD.LOG.
| Bond forming/breaking Bond 3-21G optimised structures | Bond length (Å) | Bond forming/breaking Bond frozen state 3-21G optimised structures | Bond length (Å) |
|---|---|---|---|
| C9-C1 | 2.02052 | C9-C1 | 2.02132 |
| C14-C6 | 2.01976 | C14-C6 | 2.02116 |
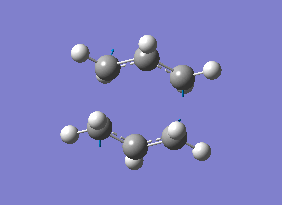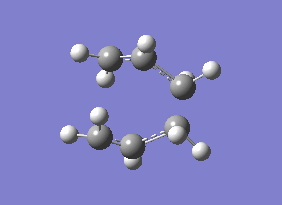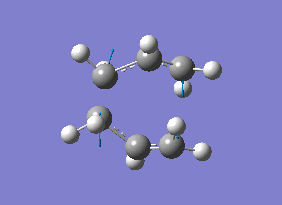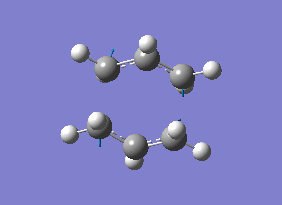
There were no significant differences in bond lengths between the two optimised transition states. This shows that the optimal distance between the terminal bond forming/breaking carbon atoms for the Cope rearrangement to occur is approximately 2.02 Å. This was backed up by the vibrational analysis at -817.91 cm-1 where the vibrational motion was consistent with the Cope rearrangement (shown in diagrams 14 and 15 below).

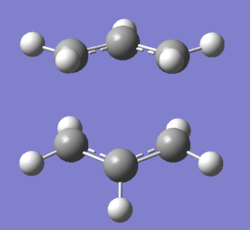
QST2 optimisation of the "Boat" transition state
The optimised anti2 Ci 1,5-hexadiene structure was used to build up the Cope rearrangement in Gaussview 5.0.9. The carbon atoms were labelled carefully as the QST2 method involves interpolating between the reactant and product in order to find the transition state between them. (Note that the B3LYP/6-31G* optimised 1,5-hexadiene was used in this section).
The atoms on both the reactant and the product were renumbered as shown in diagram 16 below.
The QST2 calculations was set up using the HF/3-21G level of theory, but the calculation failed. The .chk file for this calculation can be found here File:Qloqst2trial1.chk. During the calculation, the top allyl fragment was translated but it did not consider the possibility of a rotation around the central bonds. Therefore it became clear that the QST2 method was never going to locate the boat transition structure if these reactant and product structures were used.
The central C-C-C-C dihedral angle was changed to 0o, while the inside C-C-C bonds were modified to 100o for both reactants and products. This resulted in the structures shown in diagram 16.
The QST2 calculation was set up again using the same HF/3-21G level of theory, which produced the boat transition structure. This time the calculation was successful and the .chk file for this calculation can be found here File:Qloqst2trial2modified.chk.
| File Name | qloqst2trial2modified |
|---|---|
| File Type | .chk |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.60280 au |
| RMS GRADIENT NORM | 0.00006048 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.1585 Debye |
| Point Group | Ci |
The energy of this Boat transition state corresponds to the energy reported in Appendix 2. There was only one imaginary(negative) frequency at -840.35 cm-1, where the vibrational motion corresponds to the Cope rearrangement (diagram 19).
| Energy (Hartrees) | |
|---|---|
| Sum of electronic and zero-point energies | -231.45093 |
| Sum of electronic and thermal energies | -231.44530 |
The thermochemical data corresponds to the values reported in Appendix 2, hence the optimisation and frequency analysis were carried out correctly on Gaussview 5.0.9. These energy values will be used later in this report to calculate the activation energy of the Cope rearrangement reaction (section 2.2.6).
The same steps mentioned above was followed for the QST2 B3LYP/6-31G* optimisation of the "Boat" transition state on Gaussview 5.0.9. The .log file for this optimisation can be found here File:QLOQSTT2TRIAL2MODIFIEDOPTFREQB3LYP.LOG.

| File Name | qloQSTt2trial2modifiedOPTFREQB3LYP |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.54309 au |
| RMS GRADIENT NORM | 0.00003004 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.0612 Debye |
| Point Group | Ci |
The energy of this "Boat" transition state corresponds to the energy reported in Appendix 2, which indicates that the optimisation was carried out correctly. There was only one imaginary(negative) frequency at -530.30 cm-1, where the vibrational motion corresponds to the Cope rearrangement (diagram 21).

The energy of the B3LYP/6-31G* optimised "Boat" transition state is approximately 3 au lower in energy than the HF/3-21G optimised "Boat" transition state. As in the case of the "Chair" transition state, the structures of both HF/3-21G and B3LYP/6-31G* optimised "Boat" transition states looks remarkably similar even though they have different energies. The difference in energy values for essentially the same structures could be traced back to the basis set used. As mentioned previously in this report, the basis set is directly related to the energy of the transition state, where the basis set 6-31G* basis set has a slightly higher level of accuracy than the 3-21G basis set as it has greater flexibility and more primitives. The 6-31G* basis set gives a better description of the core and valance electrons, which will yield a lower energy. [3]
| Energy (Hartrees) | |
|---|---|
| Sum of electronic and zero-point energies | -234.40234 |
| Sum of electronic and thermal energies | -234.39601 |
The thermochemical data corresponds to the values reported in Appendix 2, hence it was concluded that the optimisation analysis was carried out correctly on Gaussview 5.0.9. These energy values will be used later in this report to calculate the activation energy of the Cope rearrangement reaction (section 2.2.6).
Intrinsic Reaction Coordinate (IRC)
The "Chair" and "Boat" transition state structures shown earlier in this report cannot be used to predict which conformer of 1,5-hexadiene the transition state will lead to. Intrinsic reaction coordinate (IRC) in Gaussview 5.0.9 allows us to do this. IRC is a minimum energy pathway which connects the reactants, transition state and products, not only does it allows us to verify whether the "Chair" and "Boat" transition states shown above are correct, it also allows us to identify any missing transition states we might have missed out.
In Gaussview 5.0.9, the reaction coordinate was only computed in the forward direction as our reaction coordinate is symmetrical and the "calculate always" option was selected for force constants. The .chk file for this calculation can be found here File:QlochairTSstateIRC.chk.
It was discovered after the calculation that it has not reached a minimum geometry (diagram 22). Since we are close to the minimum, the last point on the IRC was taken and a normal minimisation (comprising of optimisation and frequency analysis) was carried out for that point.
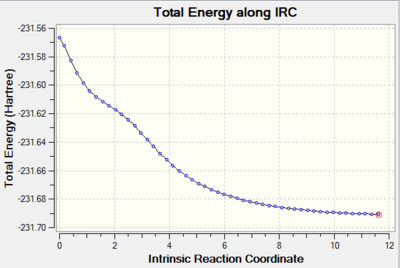
Minimisation of the last point on the IRC
The last point on the IRC (diagram 23) was minimised using the HF/3-21G level of theory in order to try and obtain the minimum geometry. The result of this minimisation can be found here File:51IRCOPTIMISATIONPART1QLOHF.LOG.

| File Name | 51IRCOPTIMISATIONPART1QLOHF |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69167 au |
| RMS GRADIENT NORM | 0.00000070 au |
| Imaginary Freq | |
| Dipole Moment | 0.38 Debye |
| Point Group | C2 |
A frequency analysis was done on this optimised structure and the following results were obtained. File:51IRCFREQPART1QLOHF.LOG.
| File Name | 51IRCFREQPART1QLOHF |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.69167 au |
| RMS GRADIENT NORM | 0.00000981 au |
| Imaginary Freq | |
| Dipole Moment | 0.38 Debye |
| Point Group | C2 |
Low frequencies --- 0 0 0 0 0 50 Low frequencies --- 63.5963 98.2281 113.3887
No negative frequencies were present and hence we can conclude that a minimum was present. By looking at the energy and the symmetry of the optimised structure in diagram 24, it was deduced that we have the gauche2 conformer of 1,5-hexadiene.
Restarting the IRC
The IRC was restarted using the same method mentioned earlier where a larger number of points was specified (80 instead of 50), this method is known to be more reliable. The .log for this calculation can be found here File:QLOCHAIROPTFREQFROZENIRC80.LOG.
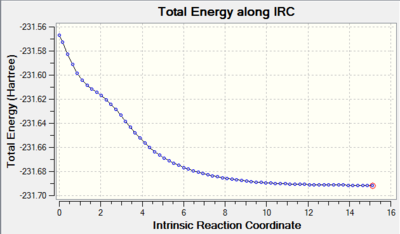
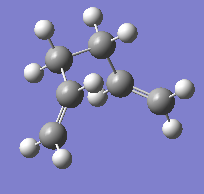
Looking at diagram 25, it is clear that we have reached the minimum geometry, where the structure at the last point is shown in diagram 26 below. The energy of this structure (-231.68160 au) is similar to the energy of the gauche2 conformer of 1,5-hexadiene in Appendix 1. We can conclude that the "Chair" transition state in this Cope rearrangement leads to the formation of the mirror image of gauche2 1,5-hexadiene.
"Boat" transition state
The .chk file from the QST2 calculation was used for this IRC calculation. The same method used for the IRC calculation of the "Chair" transition state was employed here, where a large number of points (180) was specified in this case in order to obtain the minimum geometry. The .log file for this calculation can be found here File:QLOIRCBOAT180.LOG.

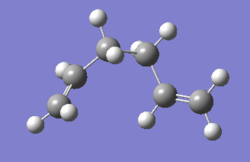
A minimum was obtained in this IRC calculation where the structure at the last point of the IRC resembles the mirror image of gauche3 in Appendix 1. This was further confirmed by looking at the energy of this structure, which has an energy of -231.69263 au and is similar to that of the gauche3 conformer in the appendix. Therefore, the boat transition state proceeds to form a mirror image of the gauche3 conformer of 1,5-hexadiene in the Cope rearrangement.
Activation energies
The "Chair" and "Boat" transition states were reoptimised using the B3LYP/6-31G* level of theory and the results were shown earlier in this report. The thermochemistry data obtained from these calculations at 0 K were used to calculate the computed activation energies for both the "Chair" and the "Boat transition states. The results are shown in tables 24 and 25 below.
| Energy (kcal mol-1) | |
|---|---|
| ΔE for "Chair" TS at 0 K | 45.70 |
| ΔE for "Boat" TS at 0 K | 55.60 |
| Energy (kcal mol-1) | |
|---|---|
| ΔE for "Chair" TS at 0 K | 34.06 |
| ΔE for "Boat" TS at 0 K | 41.96 |
The experimental activation energies are 33.5 ± 0.5 kcal mol-1 for the chair transition structure and 44.7 ± 2.0 kcal mol-1 for the boat transition structure at 0 K. The B3LYP/6-31G* optimised transition states gave activation energies that showed better correlation to the experimental values when compared to the HF/3-21G optimised energy values. This was to be expected due to the higher accuracy of the 6-31G* basis set as compared to the 3-21G basis set, where the the B3LYP/6-31G* has a higher level of accuracy and it gives a better description of the core and valance electrons. This will result in a lower energy value. The higher level of accuracy is due to the use of electron density to compute energy values by B3LYP/6-31G*, whereas HF/3-21G uses wave functions to compute energy values, which is less accurate.
The Diels Alder Cycloaddition
The Diels Alder (π4s + π2s) cycloaddtion is a pericyclic reaction[4] between a conjugated diene and an alkene to form a cyclohexene structure. It is an extremely reliable way of forming 6-membered ring structures, where there are regio- and stereochemistry control over the reaction. 6π electrons are involved in this reaction, where 4π electrons come from the cis butadiene and 2π electrons come from the alkene. The endo product is generally favoured in this reaction.
In this section, we will verify some of the known properties of the interaction between π orbitals in the Diels Alder reaction through computational methods and they include semi-empirical (AM1) and ab initio methods (HF and DFT).
Semi-empirical methods used in Gaussview 5.0.9 adheres to the prescribed Hartree–Fock framework, it obtains certain parameters from empirical data and at the same time it makes many approximations. These methods are often considered to be cheap and it requires much less time than their ab initio counterparts. AM1 (Austin Model 1) was first developed by Michael Dewar[5] which is based on the neglect of diatomic differential overlap approximation and is often used to model organic molecules.
Ab initio methods do not include any semi-empirical or empirical parameters in their equations and they are not based on any experimental data but rather they are purely based on established theoretical principles. The Hartree-Fock (HF) is the simplest ab initio method available, where the Hartree equation is used as a general solution to the Schrödinger equation. Density field theory (DFT) is widely considered to be an Ab initio method and it is known to be more accurate than HF due to the improvements made in the 1990s to better model the exchange and correlation interactions. DFT takes into account both core and valence electrons and it treats electron correlation a lot better when compared to HF, which does not treat it at all.
cis butadiene
AM1 Optimisation
AM1 semi-empirical molecular orbital method was used for this optimisation to start with. Further higher level of optimisation of cis butadiene will follow. The .log file for this AM1 optimisation can be found here File:QLOCISBUTADIENEOPT2AM1.LOG.
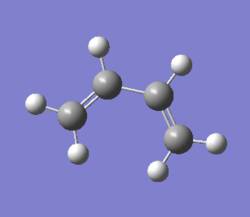
| File Name | qlocisbutadieneOPT2AM1 |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| E(RAM1) | 0.04879719 au |
| RMS GRADIENT NORM | 0.00001745 au |
| Imaginary Freq | |
| Dipole Moment | 0.04 Debye |
| Point Group | C2V |
| Number | Energy (au) | MO |
|---|---|---|
| 11 (HOMO) | -0.34 | 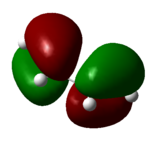
|
| 12 (LUMO) | 0.02 | 
|
HF/3-21G Optimisation
cis Butadiene was drawn on Gaussview 5.0.9 and it was optimised using the HF/3-21G level of theory. The .log file for this optimisation can be found here File:QLOCISBUTADIENEOPT2.LOG.
| File Name | qlocisbutadieneOPT2 |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -154.05394 au |
| RMS GRADIENT NORM | 0.00007879 au |
| Imaginary Freq | |
| Dipole Moment | 0.03 Debye |
| Point Group | C2V |
| Number | Energy (au) | MO |
|---|---|---|
| 15 (HOMO) | -0.33 | 
|
| 16 (LUMO) | 0.12 | 
|
B3LYP/6-31G* optimisation
cis Butadiene was drawn on Gaussview 5.0.9 and it was optimised using the B3LYP/6-31G* level of theory. The .log file for this optimisation can be found here File:QLOCISBUTADIENEOPT2DFT.LOG.
| File Name | qlocisbutadieneOPT2 |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -155.98595 au |
| RMS GRADIENT NORM | 0.00002286 au |
| Imaginary Freq | |
| Dipole Moment | 0.09 Debye |
| Point Group | C2V |
| Number | Energy (au) | MO |
|---|---|---|
| 15 (HOMO) | -0.23 | 
|
| 16 (LUMO) | 0.03 | 
|
The shape of the HOMO and LUMO orbitals are the same for all AM1, HF/3-21G and B3LYP/6-31G* optimised cis butadiene structures, where HOMO is antisymmetric and LUMO is symmetric, which was reported by Longuet-Higgins and Abrahamson[6].
The energy of the HOMO and LUMO orbitals are quite different between these three structures which were optimised using different methods. The difference in energy can be attributed to the different types of methods and basis sets used in the calculations. In the case of ab initio methods, the B3LYP/6-31G* has a higher level of accuracy and it gives a better description of the core and valance electrons, which results in a lower energy value[3]. The difference in energy is also due to the use of electron density to compute electron density by the DFT method while HF calculations require the use of wave functions to compute the energy. The AM1 semi-empirical method ignores and approximate certain integrals used to solve the Schrödinger equation, it relies on introducing new parameters based on experimental data which could give rise to HOMO and LUMO orbitals having different energies and shapes. This was not entirely true for this optimisation but we will see this effect when we optimise the ethylene and cis butadiene transition structures later.
Ethylene and cis butadiene transition structure
The transition state geometry for this Diels Alder reaction was computed using Gaussview 5.0.9 and the nature of the reaction pathway was analysed. The transition state geometry maximises the overlap between the π orbitals of ethylene and cis butadiene. The transition state has an envelope type structure which is shown in diagram 30 below. Several attempts were made to get this transition state using Gaussview 5.0.9. This envelope transition state was obtained when interfragment distance was 2.18 Å, which was close to the value reported in literature[7].
AM1 Optimisation
The transition state structure was first optimised using the AM1 semi-empirical method. The keywords "Opt=NoEigen" were used. The .log file for this optimisation can be found here File:QLODATSOPTFREQ5AM1.LOG.
| File Name | QLODATSOPTFREQ5AM1 |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| E(RAM1) | 0.11165466 au |
| RMS GRADIENT NORM | 0.00001452 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.56 Debye |
| Point Group | C1 |
| Number | Energy (au) | MO |
|---|---|---|
| 17 (HOMO) | -0.32 | 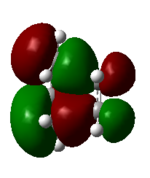
|
| 18 (LUMO) | 0.02 | 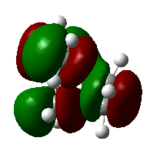
|
HF/3-21G Optimisation
The transition state structure was then optimised using HF/3-21G level of theory. The keywords "Opt=NoEigen" were used. The .log file for this optimisation can be found here File:QLODATSOPTFREQ5.LOG.
| File Name | qlodatsOPTFREQ5 |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.60321 au |
| RMS GRADIENT NORM | 0.00002745 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.58 Debye |
| Point Group | C1 |
| Number | Energy (au) | MO |
|---|---|---|
| 23 (HOMO) | -0.30 | 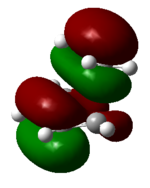
|
| 24 (LUMO) | 0.14 | 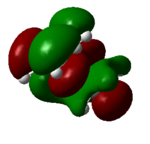
|
B3LYP/6-31G* optimisation
As mentioned earlier, since we are analysing the envelope transition state of the Diels-Alder reaction between cis butadiene and Ethylene, it is better to use B3LYP/6-31G* level of theory and like before the keywords "Opt=NoEigen" were used. The .log file for this calculation can be found here. File:QLODATSOPTFREQ5DFT.LOG.
| File Name | qlodatsOPTFREQ5DFT |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.54390 au |
| RMS GRADIENT NORM | 0.00000694 au |
| Imaginary Freq | 1 |
| Dipole Moment | 0.40 Debye |
| Point Group | C1 |
| Number | Energy (au) | MO |
|---|---|---|
| 23 (HOMO) | -0.22 | 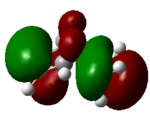
|
| 24 (LUMO) | 0.01 | 
|
The presence of an imaginary frequency indicates we have a transition state.
The HOMO of cis butadiene overlaps with the LUMO of ethylene and electrons flow from the HOMO of cis butadiene to the LUMO of ethylene. This Diels-Alder reaction between cis butadiene and ethylene is a pericyclic reaction and it is an allowed reaction because it follows the Woodward-Hoffmann rules[8]. The total electron count for this Diels-Alder reaction is 6 (4n+2, n=1) and since this reaction is thermal, it proceeds via Hückel topology involving only supra facial components, thus it follows Woodward-Hoffmann rules. Another reason why this reaction is allowed is because it is thermodynamically favourable as 2 weaker π-bonds are converted into 2 new stronger σ-bonds.
The HOMO of the transition state is antisymmetrical while the LUMO is symmetrical, this applies to all HOMO and LUMO orbitals shown above. In the transition state of the HF/3-21G and B3LYP/6-31G* optimised structures, the HOMO orbital contains a nodal plane between cis butadiene and ethylene, no nodal plane was present for the HOMO of the AM1 optimised transition structure.
The shape of the HOMO and LUMO orbitals are the same for both HF/3-21G and B3LYP/6-31G* optimised structures. However, the shape of the HOMO orbital for the AM1 optimised transition structure are different from its counterparts but the LUMO orbital for the AM1 optimised transition structure is the same as the LUMO orbitals found in HF/3-21G and B3LYP/6-31G* optimised structures. Semi-empirical methods such as AM1 use a certain number of experimental data throughout the calculation in order to make up for the fact that it ignores or approximate some of the integrals used in the solution of the Schrödinger equation. Ab initio methods (HF and DFT) are based entirely only on established theoretical principles, and it uses absolutely no experimental data. It solves all integrals without any approximation in order to obtain the solution to the Schrödinger equation, hence the occupied HOMO orbitals computed using ab initio methods can look slightly different to that of the HOMO orbitals computed using semi-empirical methods, while there were no observable change in the shape of the LUMO orbitals. It is important to note that molecular orbitals are not real and cannot be visualised physically, they are just a convenient way to visualise bonding and reactivity.
The energy of the B3LYP/6-31G* optimised transition state is slightly lower in energy than the HF/3-21G optimised transition state. The difference in energy can be attributed to the different basis sets (3-21G and 6-31G*) used in these calculations, where the the 6-31G* basis set gives a better description of the core and valance electrons and is more accurate than the 3-21G basis set, which will yield a lower energy value[3]. This could be explained by the use of electron density to compute energy values but he DFT method while HF calculations require the use of a wave function to compute the energy.
Geometry of the transition structure

| Bond type | Method | ||
|---|---|---|---|
| Semi-empirical AM1 Bond length (Å) | HF/3-21G Bond length (Å) | B3LYP/6-31G(d) Bond length (Å) | |
| C1-C2 and C3-C4 | 1.38 | 1.37 | 1.38 |
| C2-C3 | 1.40 | 1.39 | 1.41 |
| C1-C6 and C4-C5 (partly formed C-C σ bonds) | 2.12 | 2.21 | 2.27 |
| C5-C6 (Ethylene) | 1.38 | 1.38 | 1.39 |
Typical[9],[10] sp3 C-C bond length is 1.53 Å while typical[9] sp2 C-C bond length is 1.34 Å. The van der Waals radii of the carbon atom is 1.70 Å, which was given by Bondi[11] in 1964. The optimised C-C bond lengths for cis butadiene are shorter than the typical sp3 C-C and sp2 C-C bond lengths while the opposite is true for ethylene, where the optimised bond length is longer than the typical sp2 C-C bond length.
The difference between the optimised C-C bond lengths and the the typical C-C bond lengths can be attributed to the fact that this is a transition state, where both ethylene and cis butadiene have partial double bond character. The C5-C6 bond is losing its double bond character as it is about to bond with cis butadiene in the transition state to form cyclohexene, hence this results in the lengthening of the C-C bond, making it longer than the typical sp2 C-C bond length.
The partly formed C-C σ bond is significantly longer than the typical sp3 and sp2 bond lengths as the ethylene is still approaching the cis butadiene structure in the transition state to form cyclohexene.
IRC
As mentioned earlier, IRC allows us to connect the reactants, transition state and products together and it allows us to verify whether the optimised transition state structures shown above are correct and to see if any other transition state structures are present.
The reaction coordinate was only computed in the forward direction and the "calculate always" option was selected for force constants. HF/3-21G level of theory was used and 200 points were computed along this IRC to ensure it has reached a minimum. The .chk file for this calculation can be found here File:QlodatsIRC350.chk.
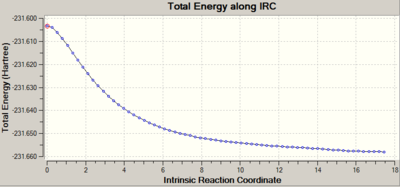

Diagram 32 illustrates the IRC energy pathway, indicating that a minimum has been reached. 200, 250 and 350 points were calculated to ensure that a minimum was reached. The structure at point 67 along the IRC energy pathway was determined to have a minimum energy. This structure matches the syn-gauche approach between cis butadiene and ethylene in Bernadi et. al.[12], where it states that this syn-gauche structure is consistent with the minimum on the potential energy surface.
Vibrational motions of the optimised structures
AM1 optimised transition state
The vibrations that corresponds to the reaction pathway was at a frequency of -956.06 cm-1. The displacement vectors illustrates the vibrational motion and is shown in diagram 34 below. The vibrational motion shows that the Diels-Alder cycloaddtion reaction between Ethylene and cis butadiene follows a synchronous concerted mechanism, which correlates with what was reported by Bernadi et. al.[12] and it is a common example used to demonstrate the Woodward-Hoffmann rules.
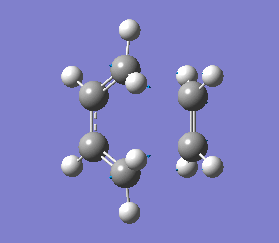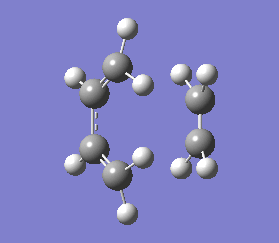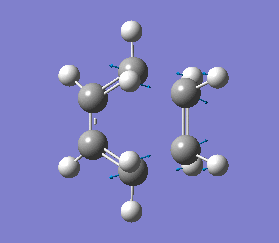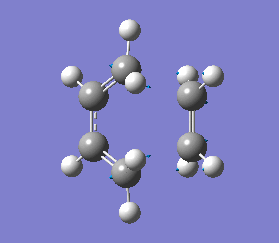
This negative vibration was then compared to the vibration with the lowest positive frequency at 147.20 cm-1, this vibrational motion does not correspond to the reaction pathway of this Diels-Alder reaction as shown in diagram 35 below.
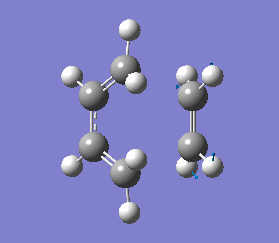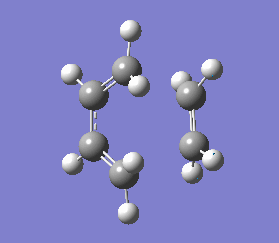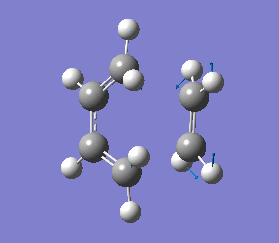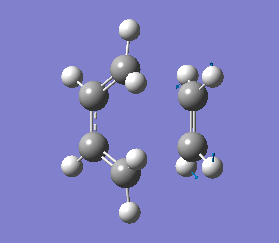
HF/3-21G optimised transition state
The vibrations that corresponds to the reaction pathway was obtained using the .log file File:QLODATSOPTFREQ5.LOG, the FREQUENCY of this vibration was determined to be at -818.69 cm-1. The displacement vectors illustrating the vibrational motion is shown in diagram 36 below.
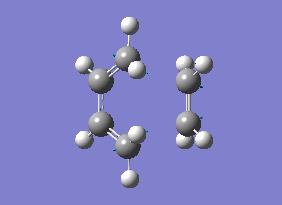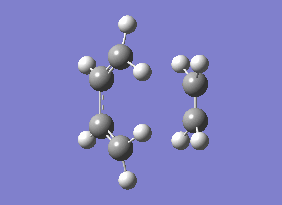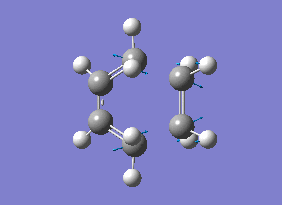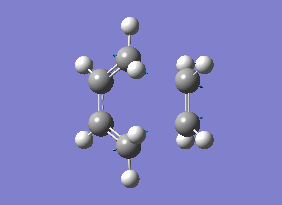
As you can see from the vibrational motion, the formation of the two bonds is synchronous, which indicates that the Diels-Alder cycloaddtion reaction between Ethylene and cis butadiene follows a synchronous concerted mechanism, which correlates with what was reported by Bernadi et. al.[12].
This negative vibrational motion was then compared to the vibrational motion with the lowest positive frequency at 166.69 cm-1, this positive vibrational motion differs drastically to the negative one and in no way corresponds to the reaction pathway as shown in diagram 37 below.
B3LYP/6-31G* optimised transition state
The vibrational motion(diagram 38) with a frequency of -525.08 cm-1 corresponds to the reaction pathway of the Diels-Alder reaction. The Diels-Alder cycloaddtion reaction between Ethylene and cis butadiene follows a synchronous concerted mechanism as shown in diagram 38. This correlates with what was reported by Bernadi et. al.[12].
This negative vibrational motion was then compared to the vibrational motion with the lowest positive frequency at 135.76 cm-1, this positive vibrational motion does not correspond to the reaction pathway.
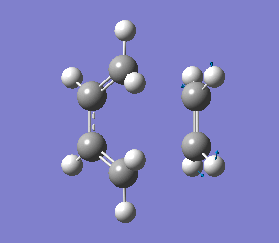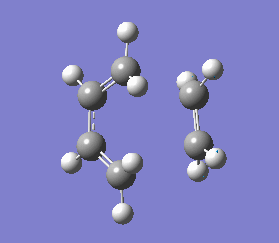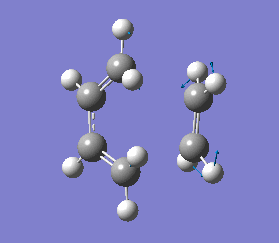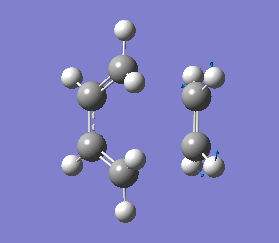
It is important to note that a negative(imaginary) frequency was obtained for each transition structure optimised at different levels. The presence of a negative frequency indicates that we have a transition state present.
Cyclohexa-1,3-diene reaction with maleic anhydride
Cyclohexa-1,3-diene reacts with maleic anhydride to give the endo adduct, which is the major product. The reaction is supposed to be kinetically controlled such that the exo transition state will be higher in energy. B3LYP has been known to underestimate the endo/exo selectivity of the Diels-Alder reaction due to problems in describing long-range dispersion interactions, this was reported in several literature sources[13],[14],[15]. Therefore HF/3-21G level of theory was used in this section.
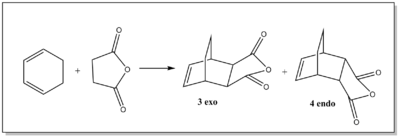
Transition structures of 3 exo and 4 endo
HF/3-21G optimisation of the 3 exo transition state
The transition state geometry for the formation of the 3 exo product was computed using Gaussview 5.0.9, at HF/3-21G level of theory where the interstructure distance was set at 2.26 Å The .log file for this optimisation can be found here File:QLODATSOPTFREQ3.LOG.
| File Name | QLODATSOPTFREQ3 |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -605.60360 au |
| RMS GRADIENT NORM | 0.00001179 au |
| Imaginary Freq | 1 |
| Dipole Moment | 5.94 Debye |
| Point Group | C1 |
HF/3-21G optimisation of the 4 endo transition state
The 4 endo transition state was then optimised using Gaussview 5.0.9 using HF/3-21G level of theory. The interstructure distance was set at 2.26 Å like before. The .log file for this optimisation can be found here File:QLODATSOPTFREQ34ENDO1.LOG.
| File Name | qlodatsOPTFREQ34endo1 |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -605.61037 au |
| RMS GRADIENT NORM | 0.00002144 au |
| Imaginary Freq | 1 |
| Dipole Moment | 6.71 Debye |
| Point Group | C1 |
The energy of the 3 exo and 4 endo transition states are -605.60360 au and -605.61037 au respectively, where the 4 endo transition state is lower in energy than the 3 exo transition state. The energy difference between the two transition states is approximately 0.00677 au (17.774636 kJ mol-1). This shows that the 4 endo transition state for this Diels-Alder reaction is more favourable and the reason for this was reported by Alder[16], where the 4 endo transition state resulted in a maximum accumulation of double bonds due to the orientation of cyclohexa-1,3-diene and maleic anhydride, where favourable secondary orbital interactions leads to a net stabilisation of the transition state. Another possible reason was proposed by Woodward and Hoffmann[8], where the endo transition state leads to an interaction between occupied orbitals with unoccupied orbitals, make it more favourable over the endo transition state due to orbital symmetry.
Bond Lengths

The bond lengths of the partly formed σ C-C bonds and the other C-C distances of the HF/3-21G optimised transition states was measured and the results are shown in the table below.
| Bond type | ||
| HF/3-21G optimised 3 exo transition state (Å) | HF/3-21G optimised 4 endo transition state (Å) | |
| 1. Partly formed C5-C8 and C6-C7 bonds | 2.26 | 2.23 |
| 2. C1-C2 and C3-C4 | 1.37 | 1.37 |
| 3. C2-C3 | 1.40 | 1.40 |
| 4. C4-C5 and C6-C1 | 1.52 | 1.52 |
| 5. C5-C6 | 1.56 | 1.56 |
| 6. C7-C8 | 1.37 | 1.37 |
| 7. C7-C9 and C8-C10 | 1.37 | 1.37 |
| 8. O1-C5 and O1-C6 (through space interactions) for 3 exo | 3.19 | N/A |
| 9. C9-C6 and C10-C5 (through space interactions) for 3 exo | 2.92 | N/A |
| 10. O1-C2 and O1-C3 (through space interactions) for 4 endo | N/A | 3.10 |
| 11. C9-C3 and C10-C2 (through space interactions) for 4 endo | N/A | 2.85 |
In the 3 exo product, the substituents on maleic anhydride such as the carbonyl groups are closer to the C=C bridge, while in the 4 endo product, the carbonyl substituents on maleic anhydride are closer to the C-C bridge, this was justified by the bond lengths shown in the table above (points 8 to 11). This slight difference in structure results in a more strained 3 exo product as steric clashes between the two C=O π bonds and the C=C π bond on the bridge is present in the 3 exo product. However, this does not occur in the 4 endo product because carbonyl substituents are closer to the C-C bridge and not the C=C bridge, where the C-C σ bond is smaller in size than the C=C π bond.
The partly formed C5-C8 and C6-C7 σ bonds are shorter in the 4 endo transition state as compared to the 3 exo transition state. This indicates that the two C-C σ bonds between C5-C8 and C6-C7 forms more readily in the 4 endo transition state as compared to the 3 exo transition state, which reinforces the fact that the 4 endo transition state is more favourable in this Diels-Alder reaction.
No literature reference containing the C-C bond lengths computed at HF/3-21G level of theory was found for this Diels-Alder reaction.
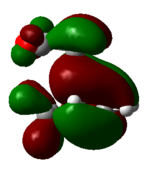
HOMO of the 3 exo and 4 endo transition states
The HOMO orbitals of both transition states were plotted using the optimised structures shown previously. They are shown in table 42 below.
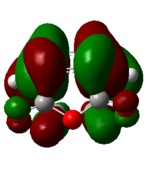
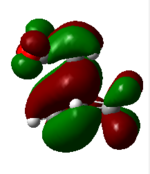
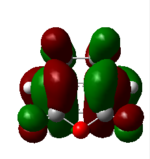
| Number | Energy (au) | Front view | Back View | Side view | Top view | |
|---|---|---|---|---|---|---|
| 47 (HOMO) 3 exo | -0.32 |  |
 |
 |
| |
| 47 (HOMO) 4 endo | -0.32 |  |
 |
 |
|
The nodal properties of the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system suggests the orbitals of the -(C=O)-O-(C=O)- fragment do not take part in the "secondary orbital overlap effect" and it does not contribute in any form towards the stabilisation of the transition state. These HOMO orbitals also illustrate the strong presence of the "secondary orbital overlap effect" between the C=C π bonds of cyclohexa-1,3-diene and maleic anhydride in the 4 endo transition state, thus resulting in 4 endo having a lower energy than the 3 exo transition state.
Further Discussion

These calculations fail to explain in greater detail the stereospecificity of the Diels-Alder reaction. The Diels-Alder reaction between cis butadiene and ethylene can either be stereospecific or non-stereospecific as reported by Sauer and Sustmann[7]. The diagram shown above illustrates the formation of a zwitterion intermediate where rotation about single bonds could lead to a non-stereospecific reaction if such rotations are faster than the rate of ring closure. On the other hand, if the opposite is true, the reaction will be stereospecific. The proximity between the two charges in the zwitterion in the 4 endo transition state stabilises the structure thus making this transition state more favourable. Zwitterions are just one of the few proposed resonance structures that could be used to describe the mechanism.
Lam et al.[13] took into account the activation barriers and dissection into interaction and distortion energies of both the endo and exo transition states, which was not considered in the calculations of this experiment. They concluded that the interactions at the endo transition state are more stabilising than those at the exo transition state by a large margin regardless of the level of theory used to compute the transition states.
Temperature effects on the Diels-Alder reaction was ignored in the calculations shown above. It is known that substituted dienophiles containing electron withdrawing groups (i.e. maleic anhydride) and electron donating groups reacts at a lower temperature and pressure which results in relatively high yields.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 B. W. Gung, Z. Zhu and R. A. Fouch , J. Am. Chem. Soc., 1995, 117, 1783-1788.
- ↑ 2.0 2.1 2.2 B. G. Rocque, J. M. Gonzales and H. F. Schaefer III , Molecular Physics, 2002, 100, 441-446.
- ↑ 3.0 3.1 3.2 D. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real World Problems, New York, John Wiley and Sons, 2004, 232.
- ↑ F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry: Part B: Reactions and Synthesis, New York, Springer, 2007, 5, 474-526.
- ↑ M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902.
- ↑ H. C. Longuet-Higgins and E. W. Abrahamson, J. Am. Chem. Soc., 1965, 87, 2045-2046.
- ↑ 7.0 7.1 J. Sauer and R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980, 19, 779-807.
- ↑ 8.0 8.1 R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395-397.
- ↑ 9.0 9.1 W. Brown, C. Foote, B. Iverson and E. Anslyn, Organic Chemistry, Belmont, Brooks/Cole, 2011, 6, 51.
- ↑ H. Bernstein, Trans. Faraday. Soc., 1961, 57, 1649-1656.
- ↑ A. Bondi, J. Phys. Chem., 1964, 68, 441-451.
- ↑ 12.0 12.1 12.2 12.3 F. Bernadi, A. Bottoni, M. J. Field, M. F. Guest, I. H. Hiller, M. A. Robb and A. Venturini, J. Am. Chem. Soc., 1988, 110, 3050-3055.
- ↑ 13.0 13.1 Y-H. Lam, P. H-Y. Cheong, J. M. Blasco Mata, S. J. Stanway, V. Gouverneur and K. N. Houk J. Am. Chem. Soc., 2009, 131, 1947-1957.
- ↑ C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer III and P. v. R. Schleyer, J. Comput. Chem., 2007, 38, 344.
- ↑ S. Tsuzuki and H. P. Luthi, J. Chem. Phys., 2001, 114, 3949.
- ↑ K. Alder and G. Stein, Angew. Chem., 1937, 50, 510.
