Rep:Mod:phys3xc1412

Cope Rearrangement

Cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic cycloaddition. The discussion below is focus on the optimisation of reactant, transition state and product structure of the above reaction.

Optimise Starting Material and Product

Optimised Gauche 1,5-hexanediene, C2 symmetry

First, the starting 1,5-hexadiene with a ‘gauche’ linkage was optimised at HF/3-21G level of theory. Total Energy of the optimised structure was determined to be -231.68771610a.u, which shows agreement with Appendix1 ^[1]. 'Gauche' configuration. It has a C2 symmetry.

Then a 1,5-hexadiene with an ‘anti’ linkage was optimised at the same level of theory. For this structure total energy of -231.69253528a.u. was obtained. By comparing to Appendix1^[1], it was determined that it has the same energy as 'anti2' configuration. The point group for it was determined to be Ci.

Optimised Anti2 1,5-hexanediene, Ci symmetry

Afterwards, 'anti2' structure was re-optimised at B3LYP/6-31G* level of theory. 6-31G* is a higher level of theory because apart from s and p polarisation, it also takes d-type polarisation on carbon atoms into account. ^[2] (If you had done a HF/6-31G* calculation, which also includes d orbitals for polarization, would you expect the same level of accuracy? João (talk) 12:44, 22 December 2014 (UTC)) Therefore, it would give us more accurate result. The energy computed was -234.61170458a.u., which is lower than the energy calculated at HF/3-21G level of theory. The symmetry information obtained from both calculations(HF/3-21G and B3LYP/6-31G*) remains the same(Ci) (If your central bond had been re-optimized to 5Å, the symmetry point group would have been the same, but the geometries would have been significantly different João (talk) 12:44, 22 December 2014 (UTC)) . Therefore, there is not much change in the overall geometry. However, compare to HF/3-21G calculation, there is a slight increase in dihededral angles and bond lengths in B3LYP/6-31G* calculation.

Some more optimisations at HF/3-21G level of theory had been done and 8 out of 10 structures in Appendix 1^[1] were found. The other 2 were not obtained due to the shortage of time. 'Gauche3' appears to be the lowest energy conformer. A study carried by Gung and Zhu^[3] did the same calculation but at 6-31G* level of theory (6-31G* is not a level of theory, it is a basis set. A level of theory is a combination of basis set and method/approximations to find the electronic energy of the system João (talk) 12:44, 22 December 2014 (UTC)) . They suggested that gauche comformers are in general, lower in Energy. This can be explained by a favourable hyper-conjugation interaction between C-H sigma orbital and C=C pi* orbital that only presents in gauche conformers. Because this trend cannot be observed in the calculation I've done, it is very likely that HF/3-21G theory did not take this interaction into account.

Table1. Energy of Other Conformers
	Gauche2	Gauche3	Gauche4	Gauche6	Anti3	Anti4
Appearance
Energy	-231.69166701a.u.	-231.69266122a.u.	-231.69153035a.u.	-231.68961573a.u.	-231.68907066a.u.	-231.69097055a.u.
Point Group	C2	C1	C2	C1	C2h	C1

A frequency calculation was then done on a B3LYP/6-31G* optimised anti-2 stucture. It confirms that this structure is a minimum because all the vibrational frequencies are real. Some thermochemistry information were recorded in the table below.

Table2. Summary of Thermalchemistry Data from Frequency Calculation
Sum of electronic and zero-point Energies	-234.469259 a.u.	0K, E = E_elec + ZPE
Sum of electronic and thermal Energies	-234.461965a.u.	298K, 1atm, E = E + E_vib + E_rot + E_trans
Sum of electronic and thermal Enthalpies	-234.461021a.u.	298K, 1atm, H = E + RT
Sum of electronic and thermal Free Energies	-234.507881a.u.	298K, 1atm G = H - TS

Optimisation of 'Chair' and 'Boat' Transition Structure

All calculation in this section were done at HF/3-21G level of theory unless otherwise stated.

A fragment of CH₂CHCH₂ was optimised then pasted to a new file twice. They were arranged in such away that the structure is an approximate chair transition state(TS).

If the guessed structure is very close to the actual TS structure, a direct optimisation to TS can be performed. One thing to be noted is that whenever we are calculating frequency, ‘Opt=NoEigen’ should be entered in the Additional keyword box to avoid calculation crash. If the guessed structure corresponds to a point far away from TS on the potential energy surface, the curvature done to minimum would be different. If the calculation can be performed successfully, it means the guessed structure is a good approximation. The TS structure could therefore, be calculated in this way. This calculation takes approx.5 minutes. From frequency calculation, an imaginary frequency of 818.08cm^-1 was observed. It represents a negative curvature on the potential energy surface, i.e.a transition state. The animation on the right hand side proves this imaginary frequency corresponds to the bond breaking/forming of a Cope rearrangement.

Otherwise, the transition state is usually optimised using frozen bond or quadratic synchronous transit(QST) method.

Frozen bond Method

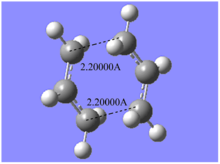
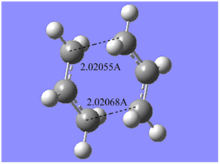
Optimised Transition Structure Directly From Guess

First, the distances between terminal atoms were frozen and the rest of the molecule was optimised to a minimum. The structure obtained here has a very similar shape as the transition structure calculated directly from reactants as can be seen in the figures below. But there is one significant difference. Here, bond forming/breaking distances are fixed.

Then, reaction coordinate was optimised using numerical gaussian to achieve the TS. A very similar result as direct optimisation was obtained. The advantage of this method is that it can save time calculating the entire Hessian space. Also, it is much simpler to operate than the next method(QST) we are going to discuss. However, the calculation would fail easily (severe error 2070, link died 9999) if the guessed structure is not a good approximation.

QST Method

Common QST methods are QST2 and QST3.

In QST2, information about both starting material and product structures are required. One should pay particular attention on the numbering of both reactant and product because they have to be the same in order for the calculation to work.

However, QST2 calculation does not allow rotation around bonds and this is the reason why the calculation failed when both of the structures provided were not close enough to the TS. Frequency calculation show an imaginary frequency at -817.90cm^-1. This means although the structure obtained is not the transition state we are looking for, it is still a transition state. (True that it is a transition state. What is wrong about it? João (talk) 13:15, 22 December 2014 (UTC))

For this specific example, the problem can be fixed by define the dihedral angle between C2-C3-C4-C5 to 0 degree and the inside C2-C3-C4 and C3-C4-C5 angles to 100 degrees. So both structures were closer to the TS on potential energy surface. The computed transition state is confirmed by the observation an imaginary vibrational frequency at 818.37cm^-1.

Another method, known as QST3, requires three structures, reactant, initial transition structure and the product, to do the calculation. Similar as QST2, the atomic numbering for all three molecules has to be consistent for the calculation to work. The advantage of this calculation is that it is quicker and the structural requirement for reactant and product are not as strict as QST2. A calculation using QST3 was not performed due to the shortage of time.

Intrinsic Reaction Coordiante

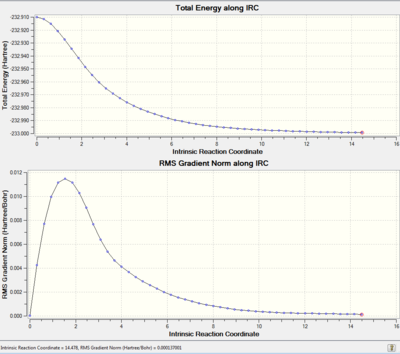
Predict Reactant and product from a transition state can be done using a method called Intrinsic Reaction Coordinate(IRC). In this exercise, because the transition state structure is symmetrical, only forward IRC was performed. Force constant was calculated at every step to provide thermochemistry information (Why do you want thermochemistry information for all points? This is not the reason to do a frequency calculation at each point. João (talk) 13:15, 22 December 2014 (UTC)) . 50 points were calculated along the IRC.

The resulting structure is closest to a Gauche2 structure(Energy -231.691382a.u.) but clearly, it has not reached a minimum yet. Two different methods were used to optimised this structure. The first method performed was a optimisation to minimum.This requires the structure to be very close to the desired local minimum. Because all ten 1,5-hexdiene conformers are very close in energy(i.e.They are close to each other on the potential energy surface). Here, the optimisation gives gauche2(Energy -231.6916704a.u.). Repeating IRC with more steps is another solution, but too many steps can let it go across the local minimum and ending up in a wrong minimum structure or even somewhere in between if force constant was not calculated frequently enough . When it was set for 100 steps and 1 force constant calculation, instead of Gauche2, the structure obatined is closer to a Gauche4. It is also possible to run IRC and compute force constant at every step. This is the most accurate method, but it is very time consuming and not always possible for large, complex system. This was not performed due to the shortage of time.

Activation Energy

Chair Transition State(obtained by frozen bond method) and Boat Transition State(obtained by QST2) at HF/3-21G level of theory were re-optimised at B3LYP/6-31G* level of theory. Thermochemistry data was obtained by operating a frequency(B3LYP/6-31G*) on the re-optimised structures. (Did you check you had only one imaginary frequency in each case? Are the geometries very different for each method? João (talk) 13:15, 22 December 2014 (UTC))

Table3. Summary of Energies(In a.u.)
	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic Energy	Sum of Electronic and Zero-Point Energies	Sum of Electronic and Thermal Energies	Electronic Energy	Sum of Electronic and Zero-Point Energies	Sum of Electronic and Thermal Energies
		at 0K	at 298K		at 0K	at 298K
Chair TS	-231.69253528	-231.466704	-231.461348	-234.55695493	-234.414919	-234.408990
Boat TS	-231.60280204	-231.450927	-231.445299	-234.54309010	-234.402351	-234.396010
Anti2	-231.692535278	-231.539540	-231.532564	-234.61170458	-234.469259	-234.461965

Activation energies were calculated using Anti2 as reactant molecule therefore the results obtained can be compared with appendix1^[1].

Table4. Summary of Activation Energies(In kcal/mol)
	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0K	at 298K	at 0K	at 298K	at 0K
	45.7014	44.6924	34.0641	34.1758	33.5+/-0.5
E_actBoat	55.6035	54.759	41.9581	41.3251	44.7+/-0.5

1 Hartee(a.u.) = 627.509kcal/mol

Activation energies obtained show good agreement with Appendix1^[1]. It can be seen that activation energies calculated at 6-31G* level of theory is closer to experimental data.

Diels Alder Cycloaddition

Optimisation of cis-butadiene

The structure of cis-butandiene is optimised to a minimum before we view its HOMO and LUMO molecular orbital(MO). HOMO MO is antisymmetric with respect to the plane while LUMO MO is symmetric. (<psna style="color:gray">What level of theory was used in these calculations? João (talk) 15:43, 22 December 2014 (UTC))

Transition state

The first temptation to optimise butadiene, ethylene cycloaddition TS was direct optimisation. However,the calculation failed(severe error 2070. Link died 9999) (This error message is very uninformative and tells you very little on why the calculation failed. You should search the log file for error or warning informations. João (talk) 15:43, 22 December 2014 (UTC)). This means that the structure I generated was far away from the actual transition structure. Then frozen bond method was used and a TSe was obtained. This is confirmed by the observation of an imaginary frequency at -832.01cm^-1. This TS structure belongs to the point group Cs, the new partly formed sigma C-C bond's bond length is 2.11962Å.

Vibration corresponds to the lowest positive frequency

Typical sp³-sp³ and sp²=sp² C-C bondlengths are 1.53Å and 1.45Å respectively.^[4] The van der Waals radius of the C atom is 1.7Å^[5] Although the partly formed sigma C-C bond is longer than sp³-sp³ C-C single bond, but it is within twice of the carbon van der Waals radii(3.4Å). It means that there is an attractive interaction between those two carbon atoms.This attraction is likely to be the main driving force for the TS-product transition.

Animation on the right hand side shows the transition state found corresponds to Diels-Alder reaction TS. It also shows that the formation of those two bonds are sychronous.The lowest positive frequency(146.94cm^-1) corresponds to a rotation mode as can be seen in the animation.This rotational vibration is in the direction perpendicular to the reaction coordinate. Therefore, it does not contribute to the structure or energy of transition state. (What do you mean by this last sentence? What you can say is that it this motion does is not involved in the reaction coordinate. João (talk) 15:43, 22 December 2014 (UTC))

HOMO and LUMO of the transition state are shown in the figure below.

Compare to the HOMO and LUMO of cis-butandiene, we can conclude that the HOMO of this TS is the combination of cis-butandiene HOMO and ethylene LUMO; LUMO of this transition state is the combination of cis-butandiene LUMO and ethylene HOMO. From the figure above, good overlap between molecular orbitals can be observed. This means the reaction is allowed.

The selection rule of percyclic reaction was discovered by Dewar and Zimmerma independently^[6] and it is summarised in the table below.

Table2. Pericyclic Reaction Selection Rule^[6]
Condition	Electron Count	Stereochemistry	Topology
Heat	4n+2	Suprafacial	Hückel
Light	4n	Suprafacial	Hückel
Heat	4n	Odd antarafacial	Möbius
Light	4n+2	Odd antarafacial	Möbius

Since the condition for Diels-Alder reaction is thermal and involves only suprafacial components, the electron count must be 4n+2 to ensure the product is of the same electronic excitation as the reactants. ^[6] This reaction involves 6 electrons, which full fills the electron count condition. Therefore, it is thermally allowed provided if interacting MOs of the reactants are close in energy. (Are they?</span João (talk) 15:43, 22 December 2014 (UTC))

Regioselectivity

The gap between interacting HOMO(diene) and LUMO(dienophile) can be narrowed down by using reactants with suitable substituents. Electronwithdrawing groups(Carbonyl groups in this case) can lower the LUMO in the dienophile and Electrondonating groups can rise the HOMO in the diene. A smaller energy gap leads to a lower activation energy and therefore, a more facile reaction.

Both endo and exo TSs were calculated using frozen bond method. The distance between the bond forming carbons were initially set to be 3Å to perform an optimisation to minimum calculation. Afterwards, we unfrozen reaction coordinate and optimise the resulting structure to a transition state. Optimised bond forming distance for endo transition state was determined to be 2.17045Å. An imaginary frequency of -812.21cm^-1 confirms that a transition structure was obtained. For endo transition state, bond forming distance of 2.16239Å and an imaginary frequency of -806.40cm^-1 were recorded. The relative energy for endo and exo were calculated to be -0.05150480a.u. and -0.05041985a.u. respectively.

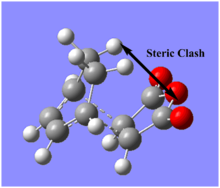
In the endo structure, carbonyl groups of maleic anhydride and -CH=CH-CH=CH- of cyclopentadiene are syn to the reaction coordinate, while in the exo product, they should be in an anti arrangement.

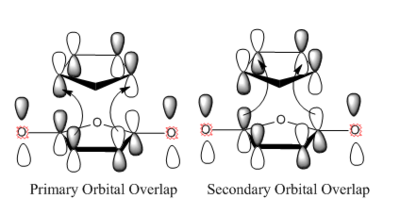
In the exo isomer, the -CH₂CH₂- bridge staggeres the anhydride ring causing more steric hindrance. ^[7] This steric clash also affected the bond forming distance in the transition state. In endo isomer this distance is 0.00806Å shorter than in the exo isomer. Apart from steric effect, endo isomer is also stabilised by a phenomena called secondary orbital orverlap. Secondary orbital overlap, defined as a positive overlap of a non-interactive frame in the frontier molecular orbitals of a pericyclic reaction^[8]. This is only possible for endo isomer as demonstrated in the diagram below.^[8] Although exo TS is more stained and is not stabilised by secondary orbital overlap, it is still lower in energy and therefore, exo product would be the thermaldynamic product. (span style="color:gray">From your values above the activation energy for the endo transition state seems lower than for exo. Why is exo the thermodynamic product? João (talk) 15:43, 22 December 2014 (UTC))

One thing to be noted is that secondary orbital overlap is not affected by the orbitals which take part in bonding. And it would not be affected by other intermolecular interaction neither.^[8]

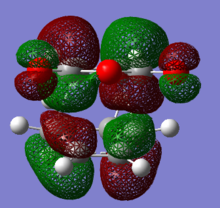
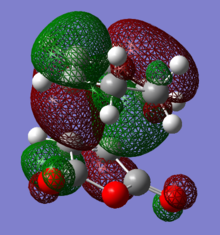
HOMO and LUMO of both endo and exo transition states are shown below.According to the discussion above, we would expect to see an secondary orbital overlap between carbonyl carbons and diene backbone. However, the orbital diagrams did not show an interaction as such. The reason of this may be the limitation of the theory level(AM1) we are using. AM1 belongs to a family called NDDO(Neglect of Diatomic Differential Overlap),in which overlap matrix is replaced by a unit matrix. In these methods, overlapping of atomic orbitals of different elements are ignored.^[9] Therefore, oxygen atomic orbital was not take account into the MO calculation (This is incorrect. The fact that some/most terms of the overlap matrix are neglected just simplifies the secular equations. Atomic orbitals of oxygen contribute to the molecular orbitals in the same way as the orbitals of all other atom. João (talk) 15:43, 22 December 2014 (UTC)). MOs below show evidence of this, in any case, it appears no overlap between oxygen orbitals and the MO.

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 Imperial College London Teaching Material https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
↑ W.L.Jorgensen, D. Lim, J.F.Blake, "Ab Initio Study of Diels-Alder Reactions of Cyclopentadiene with Ethylene Isoprene, Cyclopentadiene, Acrylonitrile, and Methyl Vinyl Ketone", J. Am. Chem. Soc., 1993, 115, 2936-2942.DOI:10.1021/ja00060a048
↑ B.W.Gong, Z.H.Zhu, "Conformational Study of 1,5-Hexadiene And 1,5-Diene-3,4-Diols", J. Am. Chem. Soc., 1995, 117, 1783-1788.DOI:10.1021/ja00111a016
↑ F.H.Allen, O.Kennard, D.G.Watson, "Tables of Bond Lengths determined by X-ray and Neutron Diffraction. Part1. Bond Lengths in Organic Compounds", J. Am. Chem. Soc.PERKIN TRANS., 1987, ii, s1-s19.DOI:10.1039/P298700000S1
↑ R.S.Rowland, R.Taylor "Intermolecular nonbonded contact distances expected from van der Waals radii", J. Phys. Chem., 1996, 100(18), 7384-7391.DOI:10.1021/jp953141
↑ ^6.0 ^6.1 ^6.2 H.Rezepa "http://www.ch.imperial.ac.uk/local/organic/pericyclic/p1_rules.html'DOI:10042.a3uxp
↑ Clayden, Jonathan; Greeves, Nick; Warren, Stuart; Wothers, Peter (2001). Organic Chemistry (1st ed.). Oxford University Press. ISBN 978-0-19-850346-0.
↑ ^8.0 ^8.1 ^8.2 Fleming, Ian (1978). Frontier Orbitals and Organic Chemical Reactions (1st ed.). Wiley. ISBN 0-471-01819-8.
↑ Leach, Andrew R. (2001). Molecular Modelling. Pearson Education Limited. ISBN 0-582-38210-6.

[ic-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 Imperial College London Teaching Material https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3

[ja00060a048-2] W.L.Jorgensen, D. Lim, J.F.Blake, "Ab Initio Study of Diels-Alder Reactions of Cyclopentadiene with Ethylene Isoprene, Cyclopentadiene, Acrylonitrile, and Methyl Vinyl Ketone", J. Am. Chem. Soc., 1993, 115, 2936-2942.DOI:10.1021/ja00060a048

[3] B.W.Gong, Z.H.Zhu, "Conformational Study of 1,5-Hexadiene And 1,5-Diene-3,4-Diols", J. Am. Chem. Soc., 1995, 117, 1783-1788.DOI:10.1021/ja00111a016

[jaP298700000S1-4] F.H.Allen, O.Kennard, D.G.Watson, "Tables of Bond Lengths determined by X-ray and Neutron Diffraction. Part1. Bond Lengths in Organic Compounds", J. Am. Chem. Soc.PERKIN TRANS., 1987, ii, s1-s19.DOI:10.1039/P298700000S1

[ja953141-5] R.S.Rowland, R.Taylor "Intermolecular nonbonded contact distances expected from van der Waals radii", J. Phys. Chem., 1996, 100(18), 7384-7391.DOI:10.1021/jp953141

[percyclic-6] 6.0 ^6.1 ^6.2 H.Rezepa "http://www.ch.imperial.ac.uk/local/organic/pericyclic/p1_rules.html'DOI:10042.a3uxp

[7] Clayden, Jonathan; Greeves, Nick; Warren, Stuart; Wothers, Peter (2001). Organic Chemistry (1st ed.). Oxford University Press. ISBN 978-0-19-850346-0.

[fleming-8] 8.0 ^8.1 ^8.2 Fleming, Ian (1978). Frontier Orbitals and Organic Chemical Reactions (1st ed.). Wiley. ISBN 0-471-01819-8.

[9] Leach, Andrew R. (2001). Molecular Modelling. Pearson Education Limited. ISBN 0-582-38210-6.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]