Rep:Mod:phys3tg1412
Introduction
This computational exercise involved the use of Gaussian software to calculate and identify transition states of various reactions. The reactions dealt with in this exercise involved a Cope rearrangement, where the reactants and products were optimized at Hartree-Fock and DFT levels of theory. The geometries of the conformers resulting from the Cope rearrangement were estimated, and optimized to a minimum on the potential energy surface. Guess structures were compared to a reference table provided. The "Chair" and "Boat" transition structures were also constructed. The initial guess TS was optimized to check if it corresponded to a saddle point. This was done by carrying out frequency calculations and finding one imaginary frequency, which corresponded to a saddle point on the potential energy surface. Transition state optimization was carried out using a few methods:
-computation of an initial force constant matrix
-frozen coordinate method
-QST2
-QST3
each of which will be explained throughout the report. Activation energies were also calculated at HF and DFT levels of theory, and results compared to pre-calculated and experimental values.
This experiment also involved the Diels Alder Cycloaddition reaction. This part of the task involved locating transition structures of two systems; a prototypical reaction involving ethylene and 1,3-cis butadiene, and one involving maleic anhydride with cyclohexa-1,3-diene. MO's were analysed and these were used to rationalize resulting reactants.
Gaussian was the electronic structure program used for the exercise. This particular software makes use of Gaussian type orbitals instead of Slater type orbitals. Gaussian type orbitals (GTO) use functions in place of atomic orbitals in the linear combination of atomic orbitals approximation, to enact the electron orbitals. Although using Slater basis sets for computational purposes contains basis elements closer to the actual solution, implementing GTO's are much faster- the advantage being the Gaussian Product Theorem. This theorem provides vast simplification when computing orbital integrals on systems with multiple atomic centres. GPT states that the sum of two integrals is a finite sum of one integral in the centre of the axis on which the two atoms are connected- and this basis can be extended across multiple atoms. However, unlike STO, GTO do not indentify the cusp of the electron wavefunction nor the exponential decay. Please refer to reference 6 for further information. For this reason, using GTO's requires more orbitals to increase the accuracy, thereby using up CPU time- a very expensive method. Nevertheless, the speed of electron orbital integrals heavily outweighs the requirement of larger orbital numbers, and hence the long calculation time.
Cope Rearrangement Tutorial- Optimizing the Reactants and Products
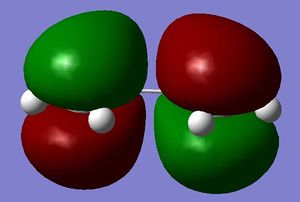
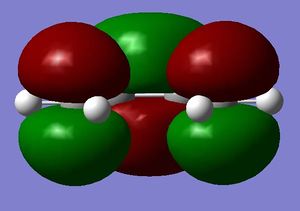
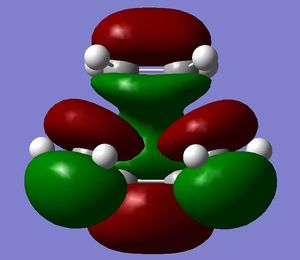
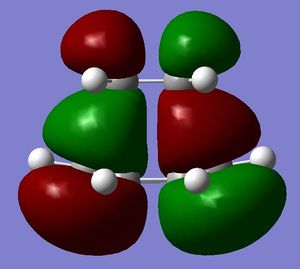
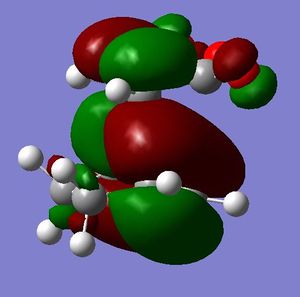
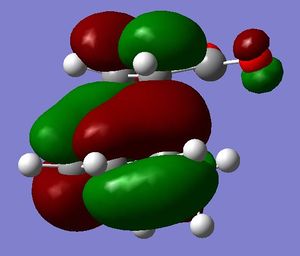
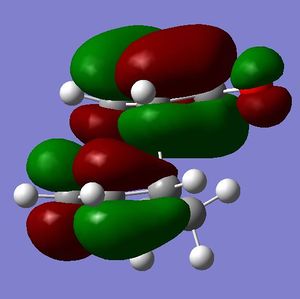
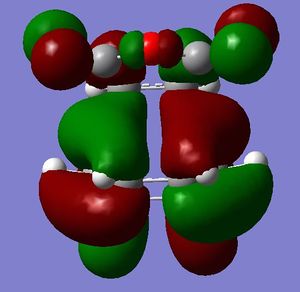
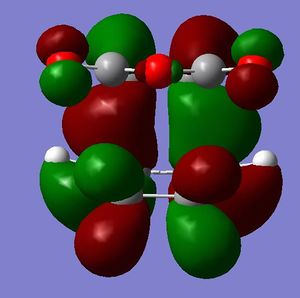
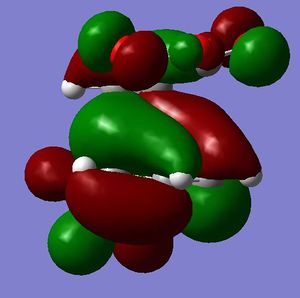
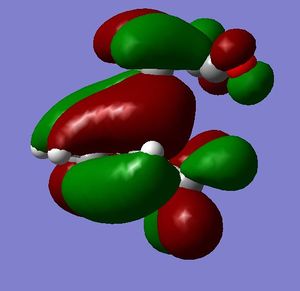
[3,3]-sigmatropic shifts are pericyclic reactions which involve six electrons. The Woodward-Hoffman Rules predict that this reaction goes by suprafacially, via a Huckel TS. The mechanism of the [3,3]-sigmatropic shift has been the topic of much controversy. The exact mechanism is not fully understood as to whether it proceeds via a stepwise, concerted or dissociative method, although a concerted mechanism is most widely accepted now. It is also widely accepted that the transition structure can either be in a "chair" or a "boat" conformation. The species involved in the transition structure could be either of a few proposed structures. The most widely accepted idea is the path which involves a diradical species. The FMO diagram of this approach is shown in figure 1.
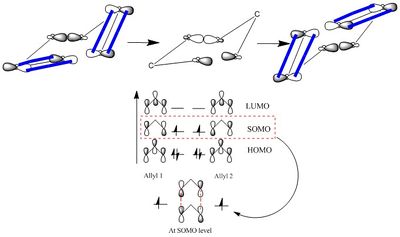
I have drawn the TS in this mechanism, using frontier molecular orbitals, as a chair conformation. The boat conformation may form too, however, the chair conformation is lower in energy, therefore preferred. This orbital picture demostrates how a chair TS (and a boat TS also) allows for good p orbital overlap between the terminal alkenes, exhibiting suprafacial orbital interaction 7. Aromatic and 1,4-diyl species are also considered to be structures which form at the TS stage. This issue is under much debate 9.
Part a (& e)
A molecule of 1,5-hexadiene was drawn using GaussView5.0.9, with anti linkage. The structure was cleaned- GaussView performed a force-field minimization on the structure drawn. The clean structure was then optimised to a minimum using HF/3-21G level of theory. The conformer which resulted corresponded to anti-2, when the energy (-231.69253527 Hartrees) was compared to Appendix 1 provided. It had a point group of Ci. A table summarizing all 'anti' conformers, located by the end of the experiment, and point groups identified is presented below.
| Anti2 | Anti1 | |||||
| Energy (Hartrees) | -231.69253527 | -231.69260230 | ||||
| Point group | Ci | C2 | ||||
| Anti3 | Anti4 | |||||
| Energy (Hartrees) | -231.68907066 | -231.69097055 | ||||
| Point group | C2h | C1 |
Anti-2 was the first conformer made. This conformer was then used in the subsequent calculations which follow in this report.
Part b (&d)
I then proceeded to construct a 'gauche' conformer. After cleaning and optimizing to a minimum (using HF/3-21G), I ended up with gauche6. Comparing energies of gauche-6 with the anti2 obtained in part a, the energy of gauche 6 was 0.00337508 Hartrees higher than anti2. The table below shows all the gauche conformers located by the end of the experiment, along with point groups.
| Gauche 1 | Gauche 6 | Gauche 5 | |||||||
| Energy (Hartrees) | -231.68771610 | -231.68916019 | -231.68961573 | ||||||
| Point group | C2 | C1 | C1 | ||||||
| Gauche 3 | Gauche 4 | Gauche 2 | |||||||
| Energy (Hartrees) | -231.69266116 | -231.69153035 | -231.69166701 | ||||||
| Point group | C1 | C2 | C2 |
Part c
Upon comparing the geometries of anti2 and gauche6 above, there is an obvious structural difference which may cause this energy difference. Conformers which contain 1 or more s-cis Csp2 - Csp3 bonds show slightly higher energy. There are only 10 distinct conformers which exist for 1,5- hexadiene, which can be told apart due to energy differences. Even though 1,5-hexadiene accommodates three C-C sigma bonds which can rotate readily, existence of symmetry means many conformers are in fact the same. Conformers which thus adopt the s-cis bond mentioned will be of higher energy. This is due to steric crowding between the vinyl terminal protons with the rest of the molecule 3. This trend, along with conformers located, correspond to literature and what is expected from conventional organic chemistry rules. The table below is a display of energies, conformers and the trend associated with the number of s-cis bonds: (Interesting observation João (talk) 13:16, 23 December 2014 (UTC))
| Conformer | Number of s-cis linkages between Csp2 and Csp3 | Energy (Hartrees) |
|---|---|---|
| Gauche 1 | 2 | -231.68771610 |
| Anti 3 | 2 | -231.68907066 |
| Gauche 6 | 1 | -231.68916019 |
| Gauche 5 | 1 | -231.68961573 |
| Anti 4 | 1 | -231.69097055 |
| Gauche 4 | 0 | -231.69153035 |
| Gauche 2 | 0 | -231.69166701 |
| Anti 2 | 0 | -231.69253527 |
| Anti 1 | 0 | -231.69260230 |
| Gauche 3 | 0 | -231.69266116 |
These results seem to follow what would normally be expected in conformation geometry and energy- the more steric repulsions between groups, the higher the energy. However, Gung et al found results which corresponded to the opposite behaviour- gauche having lower energy. In their 1995 paper 10, the group used the Møller-Plesset perturbation theory, and the 6-31G* babsis set to carry out similar calculations. In doing so, they discovered gauche on average was lower in energy. A proposed explanation was that there exists a favourable stabilising interaction between the π system of the C=C double bond and the proton on the vinyl group, labelled a CH-π interaction. The HF method does not take into account electron correlation 11 thus, many important electronic interactions may be overlooked, such as this proposed CH-π stabilising interaction. It seems strange that gauche should lead to the most energetically stable conformer at all, because it is common knowledge that any gauche conformer is subject to high steric strain. Based on results using HF and work by Gung et al, it confirms the idea that it is impossible to singly isolate the most stable conformer out of the ten mentioned, as they are all extremely close in energy. (Wouldn't that depend on temperature? João (talk) 13:16, 23 December 2014 (UTC))
Geometry Comparison
Part f
The anti2 conformer was then optimized at DFT level, a method which uses a larger basis set (The DFT method used can be used with any basis set. It is true that you used a bigger basis set compared to the HF calculation but this is intrinsic to the method. You improve your calculation in two ways: bigger basis set; better method, which in this case includes electron correlation João (talk) 13:16, 23 December 2014 (UTC)), and gives better results due to it taking into account polarisation and electron correlation 11 The resulting structure was compared to that optimized at HF level. Geometric diffrences were noticed: there were bond length differences as well as differences in dihedral angles. For the DFT optimized anti2, the 'terminal' dihedral angles (between C1-C2-C3-C4 and C3-C4-C5-C6) was measured to be 118.59926°, around 4° larger than that of HF optimized. The 'central' dihedral angle of both DFT and HF optimized remained the same, at 180°. Bond lengths differed, such that the length of C1-C2 (C5-C6 also, by symmetry) at DFT level of theory was higher by 0.01735Å compared to HF. Bond length between C3-C4 was also higher for HF compared to DFT, by 0.00457Å. Bond length between C2-C3 (C4-C5 also, by symmetry) was higher for HF compared to that of DFT. These results are to be expected. Hartree Fock method does not take into account exchange correlation (This is actually the only type of correlation included in a Hartree-Fock calculation João (talk) 13:16, 23 December 2014 (UTC)) in its One-electron Fock Operator 11. Therefore, it assumes electrons only see an average field, and ignores the possibility of individual electron repulsions. Ignoring this Coulomb correlation, HF method assumes that charges are allowed to approach each other closely, without there being any energy change. This assumption shows the molecule will be higher in energy and the bond lengths would be expected to be smaller compared to more accurate calculations or experimental results 7. This is more or less what we see here. The DFT method provides an energy which includes electron correlation as a functional of the electron denisty. DFT includes an Exchange correlation term- this takes care of individual electron-electron interactions, and potential energy as a result of the electron's charge and spin 11. The table below is a summary of gemoetrical differences between the two levels of theory:
|
|
|
| Labelled anti2 |
| Dihedral angle (°) | Bond lengths (A) | |||||
|---|---|---|---|---|---|---|
| C1-C2-C3-C4 | C2-C3-C4-C5 | C3-C4-C5-C6 | C1-C2 | C2-C3 | C3-C4 | |
| HF/3-21G | 114.69655 | 180.00000 | -114.69655 | 1.31615 | 1.50888 | 1.55273 |
| B3LYP/6-31G* | 118.59926 | 180.00000 | -118.59926 | 1.33350 | 1.50419 | 1.54816 |
Table 2: Comparing dihedral angles of anti2 conformers using HF/3-21G and B3LYP/6-316*
Part g
Energies in the output file correspond to the energy (in Hartrees) of the molecule on the potential energy surface. However, it is not enough to use these values of energy to compare to experimental values. For a good enough comparison to be made, additional parameters need to be included. These are the zero-point energies, thermal energies, thermal enthalpies and thermal free energies 17. These terms were calculated by carrying out a frequency calculation. Frequency calculations are useful- they calculate these terms as well as help characterize the point on the PES on which the molecule sits 17. I.e, it characterizes the critical point, and carries out second order energy differentials to check for minima's and saddle points. Frequency calculations were thus carried out on the DFT optimized anti2 molecule, at the same level of theory. The result showed no imaginary frequencies, only real and positive ones, confirming the idea that anti2 is a minimum.
|
|
|
| Infrared spectrum of vibrational frequencies of optimized anti2 structure, at B3LYP/6-216* level |
Above is the IR spectrum of the optimized anti2 from part g. It corresponds the to vibrations of the molecule; peaks at 3050, 3075, 3150 and 3250cm-1 correspond to =C-H alkene stretches. Peaks between 650-990cm-1 correspond to =C-H alkene bending 12. These vibrational modes and wavenumber values correctly correspond to the vibrations shown in the movie of anti2 below:
|
|
|
| Infrared spectrum of vibrational frequencies of optimized anti2 structure, at B3LYP/6-216* level |
| 298K | 0K | |
|---|---|---|
| Σ Electronic & zero point energies: | -234.469219 | -234.416154 |
| Σ Electronic & thermal energies | -234.461869 | -234.416154 |
| Σ Electronic & thermal enthalpies | -234.460925 | -234.416154 |
| Σ Electronic & thermal free energies | -234.500809 | -234.416154 |
Thermochemistry data was extracted from the output file. Σ Electronic & zero point energies corresponds to the potential energy at 0K temperature, and it also takes into account the lowest energy possible for a quantum mechanical system to have- the zero-point energy. Σ Electronic & thermal energies takes into account the energy of the molecule on the bare PES at 298.15K at 1 atm pressure, along with contributions from the three degrees of freedon- translational, rotational and vibrational modes. Σ Electronic & thermal enthalpies includes an additional correction for RT, since H = E + RT (Under which conditions is this true? João (talk) 13:16, 23 December 2014 (UTC)). Σ Electronic & thermal free energies includes the entropic free energy, from G = H - TΔS 17 (How is the entropy estimated in this case? João (talk) 13:16, 23 December 2014 (UTC)).
From the table above, we can see that the values of these energies at 0K remains the same. This suggests that there is no thermal contribution to these energies (Did you expect any thermal contribution at 0K? João (talk) 13:16, 23 December 2014 (UTC)). Formation of transition structures rely purely on kinetics.
Cope Rearrangement Tutorial- Optimizing the "Chair" and the "Boat" Transition Structures
A few different methods to compute and optimize transition structures were explored in this part of the exercise. They include a) the computation of a force constant matrix at the start of every calculation, b) using the redundant coordinate editor, the frozen coordinate method and c) the Quadratic synchronous Transit (QST2) and QST3.
Part a
A C3H5 allyl fragment was constructed and optimized using HF/3-21G level of theory. It had a C2v point group. This fragment was then used to contruct the chair and boat transition structures to follow.
Part b
This fragment was pasted into another view window, appended and arranged such that it resembled the chair transition structure. This was the guess structure for the chair transition structure. The bond breaking/forming distances were set to guess values of 2.2000Å and 2.1823Å. The guess structure is shown in the thumbnail picture.
This guess structure was optimized by computing the force constant matrix in the first step of the calculation. The force constant was then updated as the reaction proceeded. Optimization to a TS Berny and Frequency calculations, calculating first and second derivatives 15 were run on this initial structure. The additional keyword Opt=NoEigen was required in the keywords line to make sure the calculation did not crash if more than one imaginary frequency was located. If the starting structure was close to the TS and if one negative second derivative was located, the calculation would converge to the nearest saddle point and one imaginary frequency would be obtained. If the starting guess structure was to be far from the desired structure on the PES, and contained more than one negative eigenvalue, the calculation would fail or would take the reaction down a route with the largest negative eigenvalue 16. This can sometimes occur if our initial guess structure is not close enough to the transition structure 17. After the calculation was completed, vibrations were checked, and one imaginary frequency of -817.91cm-1 was found. This showed that a saddle point was indeed found.
(What does this transition state tell you about the mechanism of the reaction? Does it confirm what you anticipated in the introduction? João (talk) 13:16, 23 December 2014 (UTC))
After optimizing, the forming/breaking bonds were checked. It turned out that the distance had decreased from around 2.2000Å to 2.02114Å, each bond being broken/formed being the identical in length. The energy and point group data are summarized in the table below:
| 298K | 0K |
|---|---|
| Energy of TS | -231.61932195 |
| RMS Gradient Norm | 0.00009435 |
| Point group | C2h |
| No. of imaginary Frequencies | 1 |
| Value of Imaginary Frequency (cm-1) | -817.91 |
Part c & d
The frozen coordinate method is a method used to optimize the transition state. In this method, the structure is optimized to a minimum, all except the bond forming/breaking paths- these have their coordinates frozen, so are not minimized in the process. Once the structure has fully relaxed, the frozen coordinates are then unfrozen, second derivatives calculated along the reaction coordinate using a guess Hessian which was changed slightly to take into account the two coordinates being differentiated along, and the whole structure optimized to a transition state.
| Method of Chair TS optimization | |||
|---|---|---|---|
| Part b (Computation of force constant matrix) | Part d (Frozen coordinate method) | ||
| Bond forming/breaking distance A | 2.02048/2.02051 | 2.02071/2.02071 | |
B3LYP/6-31G* seemed to return a transition structure with bond forming/breaking distances 0.000215Å longer than that of HF/3-21G. The fact that HF does not take into account electron correlation has already been explained, and this is yet another manifestation of this difference.
Part e
Quadratic synchronous transit (QST) is a synchronous guided Quasi-Newton approach of optimizing the transition structure. The reactant and product are built, and the interpolation is carried out along the parabola which connects the two, generating an initial guess structure for the transition state in doing so 16. This part of the tutorial required an optimisation of the boat transition structure.
For successful implementation of this method, the initial guess structures of the reactant and product needs to be close enough to the true structure. The calculation will then find a structure exactly halfway between the two, providing a guess transition structure. The figures below show how the calculation can provide us with an error, if the initial guess structures constructed are not good enough to be interpolated through. The reactant and product shown were constructed initially as guess values. However, since they were not good enough to start with, an incorrect and poorly interpolated boat TS was the result. This guess boat TS was clearly wrong- the hydrogen atoms are facing the wrong way, and wrong bonds are being formed 13. From the dotted partial bonds, you can see that a bond is being broken between C atoms 3 and 4, and a bond is being formed between C atoms 1 and 6. I.e, there was simply a translation of a group of atoms across, and the calculation didn't even consider a possible rotation around the central bonds.
(The transition state is not "wrong". It is a chair transition state while you want the boat one. The dash lines have no particular meaning: in a quantum chemical calculation it is the inter-nuclear distance that is relevant, there is no a priori bonding between atoms João (talk) 13:16, 23 December 2014 (UTC))
|
|
|
| Reactant | Product |
|
|
|
| Figure X: Error given by wrong initial structure guess | Figure X: Error structure, forming and breaking incorrect bonds |
Therefore, to successfully implement the method of QST2, chemical intuition is required, to accurately locate a structure of the reactant and product close enough to the true value, in order to provide a reasonable transition structure. A few amendments were made to the guess reactant and product, which included changing the dihedral angle between the central four C atoms to 0º, and the inner angles (between C2-C3-C4, C3-C4-C5 of reactant and C2-C1-C6, C1-C6-C5 of product) to 100º. This better guess for the structures was then run under same method. These adapted structures are shown below.
|
|
|
| Structure closer to Boat TS | Boat TS |
| 298K | 0K |
|---|---|
| Energy of TS | -231.60280218 |
| RMS Gradient Norm | 0.00006536 |
| Point group | C2v |
| No. of imaginary Frequencies | 1 |
| Value of Imaginary Frequency (cm-1) | -840.02 |
The pictures above show a much better approximation for the boat transition structure. It has the correct symmetry, and one imaginary frequency of -840.02cm-1. QST2 is a very good method for approximating guess intermediate structures, however, the initial guess structures need to be good enough for a decent result, therefore, one is required to have a firm understanding of the mechanistic pathways of the reaction in question. This method is good for small bimolecular reactions. However, it often fails for more complex reactions and unimolecular pathways, as it cannot interpolate the path between reactants and products well enough to provide a sufficient guess structure.
There exists another synchronous guided Quasi-Newton approach of optimizing the transition structures. This is called the QST3 method. The difference between QST2 and QST3 is that for the latter, coordinates for a guess transition state is required. It is a more sturdy and reliable approach as the calculation will attempt to converge to the transition structure provided. The following picture shows how the guess structures were arranged for the calculation. The guess reactant, product and transition state were required in three windows in that order:
|
|
|
| QST3 calculation arrangement |
| 298K | 0K |
|---|---|
| Energy of TS | -231.60280239 |
| RMS Gradient Norm | 0.00001623 |
| Point group | C2v |
| No. of imaginary Frequencies | 1 |
| Value of Imaginary Frequency (cm-1) | -840.26 |
Geometry comparison between methods QST2 and QST3
 |
 |
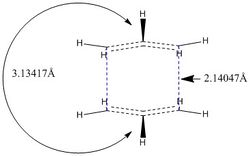| QST2 | QST3 |
There are small geometric differences in the resulting transition structures by using the two methods, although very similar. The flagpole interactions between the two "eclipsing" H atoms pointing in the same direction for the QST2 method is 3.12417A, with bond breaking/forming distances of 2.14047A. For the transition structure resulting from using QST3, the H flagpole interactions are 3.13394A and bond forming/breaking distances are 2.13924A, 0.00107A shorter than that calculated using QST2. H flagpole interactions are also 0.00023A shorter for the QST3 method compared to QST2. (Nice that you tried QST3. I would say that your differences are very small and that you are dealing with the same structure. Do you have an idea of what the uncertainty of your geometries is? João (talk) 13:16, 23 December 2014 (UTC))
Part f
So far, we have optimised transition structures by guessing and optimising starting structures, and using chemical intuition to seek transition structures which look closest to the true structure/resemble the reactants. This part of the exercise involved starting with ready optimised transition structures and tracing back the reaction coordinate pathway to identify the reactant from which it most like started from. This is called the Intrinsic Reaction Coordinate.
Using optimised Chair TS from part b, an IRC calculation was run. Starting at the top of a potential 'hill' where the transition structure sits, parameters were selected such that only the forward direction was analysed (both reactant and product were symmetrical).
(RMS Grad Norm = 0.00015225)
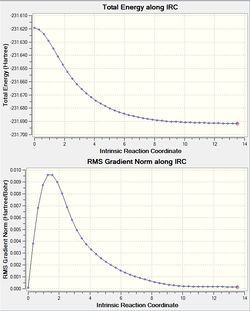
Following this pathway, the calculation resulted in a path which resulted in a gauche 2 conformation. Since all ten conformers are very close in energy, the intrinsic reaction path can take you down to any conformer (This is not necessarily true, this depends on the barriers between conformers and the details of the PES. João (talk) 13:16, 23 December 2014 (UTC)). It may well be that, in order to attain the lowest energy conformer (in our case, gauche 3) the conformer we obtained may be sitting in another well just higher in energy than the lowest energy. This is depicted in the image. After 50 steps, looking at the RMS gradient, the value of the gradient had not gone to zero. We don't expect it to go fully to zero, because this would mean we have identified a transition structure (A minimum in this case João (talk) 13:16, 23 December 2014 (UTC))for definite, and that is never the case for computational experiments or otherwise. (This is correct, but in principle you can get as close to zero as you wish by setting your convergence criteria. João (talk) 13:16, 23 December 2014 (UTC))
To attain a reactant molecule which was closer to a minimum geometry, two steps were taken. One was to optimize the last step (the reactant molecule) to a minimum and looking at the RMS gradient value. Another step taken was to increase the steps to a larger number.
Part f i
A normal optimization to a minimum was run on the last step, using HF/3-21G basis set. This was a fairly fast approach, and resulted in an RMS Gradient norm value of 0.00000474. This method, being the fastest and most convenient, it has some drawbacks. For it to work well enough, the structure must be close enough to a local minimum. If not, the optimization will lead you to a different, and potentially incorrect, geometry. For the purposes of this exercise, it seemed to work well within reason, and returned a gradient value closer to zero than before, and also returned the same conformer, gauche 2.
| 298K | 0K |
|---|---|
| Energy of minimum | -231.69166702 |
| RMS Gradient Norm | 0.00000474 |
| Point group | C2 |
| No. of imaginary Frequencies | 0 |
| Value of Imaginary Frequency (cm-1) | N/A |
Part f ii
Using the second method to obtain a structure close to a minimum, the number of steps in the IRC was increased from 50 to 100. The results returned showed no difference between that at 50 steps, and the same conformer, gauche 2 was resulted, however, the reaction converged at 44 steps instead of the 100 specified, showing that a minima was found earlier. Usually, this method is the most reliable as the more number of steps taken, the smaller the change in geometry through the reaction coordinate from the transition structure to the reactant can be monitored, and you are more likely to obtain a more reliable result. However, this method is more costly and takes a lot of time.
| 298K | 0K |
|---|---|
| Energy of minimum | -231.69157945 |
| RMS Gradient Norm | 0.00015225 |
| Point group | C2 |
| No. of imaginary Frequencies | 0 |
| Value of Imaginary Frequency (cm-1) | N/A |
Part g
In this part of the exercise, activation energies were calculated, by carrying out freq calculations at two different levels of theory, and compared; HF/3-21G and B3LYP/6-31G*.
Hartree-Fock optimized structures of the chair and boat structures from parts b), c) and d) were used in the following calculations. Taking the optimized chair transition structure from part b) (structure optimized to a TS Berny), a DFT optimization was carried out. Thermochemistry data was obtained and the activation energies were obtained from this transition structure and the reactant, optimized at same level of theory for consistency. The same procedure was carried out for the chair transition structure (optimized using frozen coordinate method) and the boat transition structure (optimized using both QST2 and QST3). The results of the theromochemistry data of each transition structure at each level of theory, are summarized in the tables below: (Did you check if one imaginary frequency remained on the second optimization? João (talk) 13:16, 23 December 2014 (UTC))
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Σ Electronic & zero point energies | Σ Electronic & thermal energies | Electronic energy | Σ Electronic & zero point energy | Σ Electronic & thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS (using part b) | -231.61932195 | -231.466694 | -231.461333 | -234.55692633 | -234.414918 | -234.408986 |
| Chair TS (using part d) | -231.61932244 | -231.466703 | -231.461343 | -234.55692633 | -234.414918 | -234.408986 |
| Boat TS (QST2 method) | -231.60280218 | -231.450929 | -231.445300 | -234.543093 | -234.402356 | -234.396012 |
| Boat TS (QST3 method) | -231.60280239 | -231.450921 | -231.445293 | -234.54307882 | -234.402356 | -234.396012 |
| Reactant (anti2) | -231.69253527 | -231.539539 | -231.532565 | -234.54307882 | -234.469219 | -234.461869 |
The calculated activation energies of each transition structure at each level of theory are summarized below. (Are all these transition structure different? Do you need to compare them all? João (talk) 13:16, 23 December 2014 (UTC))
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE Chair TS (using part b) | 45.71089311 | 44.69872109 | 34.07436621 | 33.18455845 | 33.5 ± 0.5 |
| ΔE Chair TS (using part d) | 45.70148047 | 44.692446 | 34.07436621 | 33.18455845 | 33.5 ± 0.5 |
| ΔE Boat TS (using QST2) | 55.60357249 | 54.75957289 | 41.95713427 | 41.32586021 | 44.7 ± 2.0 |
| ΔE Boat TS (using QST3) | 55.60859256 | 54.76396545 | 41.95713427 | 41.32586021 | 44.7 ± 2.0 |
The activation energies calculated were found to be similar and in good agreement with literature values 1.
The Diels Alder Cycloaddition
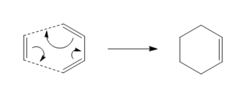
The Diels-Alder [4+2] Cycloaddition is a class of pericyclic reaction, which involves the electron 'flow' from an electron rich diene to an electron poor dienophile to form a cyclohexene. It was first discovered by Otto Paul Hermann Diels and Kurt Alder, for which they won the 1950 Nobel prize in Chemistry. This reaction provides a good synthesis route to construct six membered cyclic systems with very good control over stereochemical properties of the products. It is thought to follow a mechanism which takes it through a synchronous, concerted and cyclic transition structure 9 . However, this is a subject which is not concluded for certain, as there are hypotheses which suggest a two step mechanism could also exists, forming a diradical intermediate 9.
The Diels-Alder reaction follows orbital symmetry rules. It is a 4πs + 2πs cycloaddition, involving six electrons. It has two components the diene and the dienophile.
The HOMO of the diene interacts with the LUMO of the dienophile, resulting in the formation of two new sigma bonds. The formation of new sigma bonds is the driving force of this reaction. This is a thermally allowed suprafacial 4n+2 pericyclic reaction which proceeds via Huckel topology, with a 4π electron and a 2π electron component.
The Diels Alder reaction requires that both components involved must have the same symmetry in order for them to react.
Part i
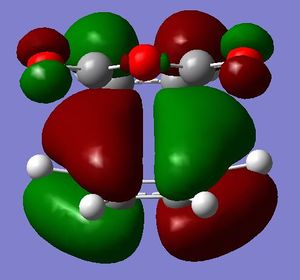
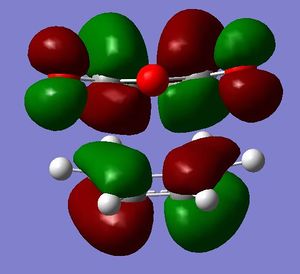
Cis-butadiene was constructed using GaussView, and symmetrized and optimized using the semi-empirical/AM1 method and basis set (AM1 is not a basis set, it is the name of a semi-empirical method ans uses a specific basis set João (talk) 13:16, 23 December 2014 (UTC)). Below are pictures of the HOMO and LUMO orbitals of ethylene and cis-butadiene.
| Ethylene | Cis-Butadiene |
|---|---|
 |
 |
| Ethylene HOMO orbital, symmetric wrt plane of symmetry | Cis butadiene HOMO, antisymmetric wrt plane of symmetry |
 |
 |
| Ethylene LUMO, antisymmetric wrt plane of symmetry | Cis butadiene LUMO, symmetric wrt plane of symmetry |
Part ii
The HOMO at the transition structure is antisymmetric with respect to the plane of symmetry. The table below presents the HOMO and the LUMO orbitals of the transition structure
| TS LUMO | TS HOMO |
|---|---|
 |
 |
| Ethylene HOMO orbital, symmetric wrt plane of symmetry | Cis butadiene HOMO, antisymmetric wrt plane of symmetry |
 |
 |
| Ethylene LUMO, antisymmetric wrt plane of symmetry | Cis butadiene LUMO, symmetric wrt plane of symmetry |
For this reaction to the transition structure, the HOMO of the butadiene has combined with the LUMO of the ethylene. Since the orbitals between these components can overlap well, this reaction is symmetry allowed. This overlap between the orbitals is allowed thermally, and whether or not a pericyclic reaction is allowed or forbidden is guided by the Woodward-Hoffman rules:
| 4n+2 electrons | 4n electrons | |
|---|---|---|
| Thermal conditions | Suprafacial | Antarafacial |
| photochemical condition | Antarafacial | Suprafacial |
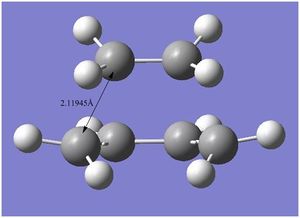
A typical sp3 C-C bond length is 1.54Å, and a typical sp2 C=C bond length is 1.35Å. The Van der Waals radius of a carbon atom is 1.7Å 4. The resulting bond length of the partly formed σ C-C bonds in the TS is 2.11945Å, from the calculation I input to Gaussian. From the obtained value, the partially forming/breaking bond is much larger than an sp3 C-C bond, an sp2 C=C bond and also larger than the Van der Waals radius of a typical carbon atom. However, it is smaller than twice the Van der Waals radius of a carbon atom, therefore, there exists favourable attractive interactions for bonds to form.
At the transition structure, the vibrations show the bond formation to be synchronous. The carbon atoms involved in forming/breaking of bonds vibrate towards each other and away in phase. The vibrations corresponding to the lowest positive frequency shows mere rotation type movements in the ethylene group, and no significant vertical vibrations between the bond forming/breaking carbon atoms in question. This is an orthogonal vibration to the vibration in the transition state, and does not contribute to the transition structure properties (This is not completely accurate. What you can say is that such movement does not contribute to the reaction path. João (talk) 13:16, 23 December 2014 (UTC)). The two vibrations are depicted in the movies below:
|
|
|
| Lowest positive frequency vibration | Vibration corresponding to reaction path at TS |
Activation energies were calculated at AM1 level, and compared to an experimental value from literature 4. The tables below summarize the energies of the transition structure, the ethylene and the butadiene molecules. These were converted to kcal/mol by multiplying by the conversion factor 1 Hartree = 627.509 kcal/mol.
|
| ||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
My results gave an activation energy value of 25.49kcal/mol, using the semi-empirical/AM1 method. This value is very close to the literature value reported of 25.1kcal/2.
Part iii
In this part of the exercise, the Diels Alder reaction of Maleic Anhydride and cyclohexa-1,3-diene was examined.
Having strong electron withdrawing substituents on the dienophile and/or electron donating substituents on diene allows the reaction to occur much easier at lower temperatures and pressures. It is believed that, in the presence of these groups, the orbitals will shift: the LUMO of the dienophile will lower and the HOMO of the diene will raise in energy. This allows a much better energy comparison between the orbitals, therefore a more facile reaction 14.
Maleic Anhydride and cyclohexa-1,3-diene were both constructed individually, symmetrised and optimized to a minimum. These were then placed in rough orientation of the endo and exo transition structures.
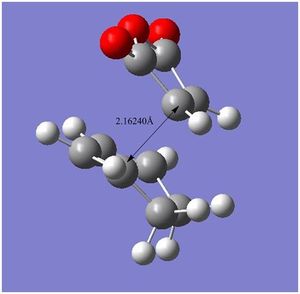
The exo transition structure was made using the frozen coordinate method. The bond forming/breaking distances were extended and set to 2.2Å. The whole molecule was optimized to a minimum, after which the frozen bonds were unfrozen, and derivatives were calculated along these bonds. The figure on the left shows the Exo transition structure, along with final optimized bond breaking/forming distance of 2.17043Å. The calculation converged, displaying one imaginary frequency of -812.13cm-1.
The clip below shows the synchronous vibration of the transition structure formed:
|
|
|
| Exo transition structure, synchronous vibration |
The endo transition structure was constructed via the method of optimization to a TS Berny. This structure was generated by orienting the components in an endo form, extending the bond breaking/forming distance to 2.2Å and minimizing to a transition state. The calculation converged and gave an imaginary frequency of -806.36cm-1. The clip below shows the synchonous vibration at the transition structure:
|
|
|
| Endo transition structure, synchronous vibration |
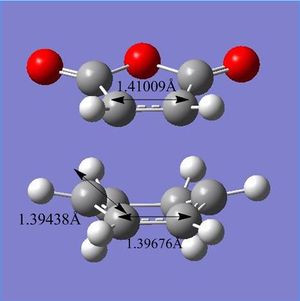
The tables below summarize the energies, geometric information and thermochemical data for the endo, exo, cyclohexa-1,3-diene and maleic anhydride. The images along the right hand side are geometry and bond length comparisons of the endo and exo at the transition structures. The bond forming/breaking distances are slightly larger (by 0.000803Å) for the exo compared to the endo. The internal carbon-carbon bonds show slight differences in geometry, the bonds are of different values for endo and exo.
|
| |||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
|
| |||||||||||||||||||||||
| ' | ' |
|
| |||||||||||||||||||||
| ' | ' |
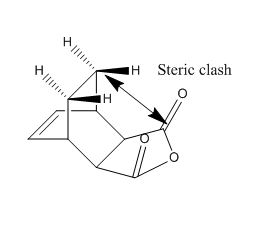
The exo transition structure is under more strain than the endo. There is more steric hindrance between the maleic anhydride carbonyl group and the hydrogen atoms sticking out on the CH2=CH2 group opposite. This is illustrated in the image below:
|
|
|
| Steric clash in exo, adapted from Clayden 2nd edition |
This, along with no secondary orbital overlap between atoms, cause the exo to be more strained.
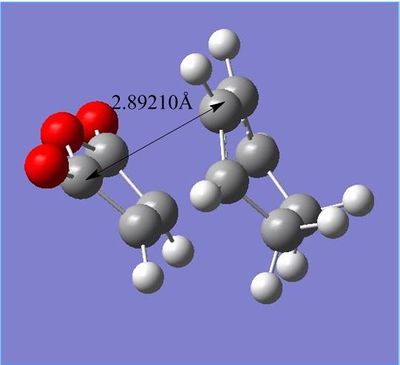
The structural differences between the two transition structures is that for endo, the two carbonyl groups on the maleic anhydride component are on the same face as the ethylene backbone of the diene in the product (or TS). The exo has the opposite structure- the two carbonyl groups on the maleic anhydride component are not superimposed, but facing away. The pictures below show the through-space interactions and distances between the endo and exo TS components:
|
|
|
| Through-space distance of endo TS | Through-space distance of exo TS |
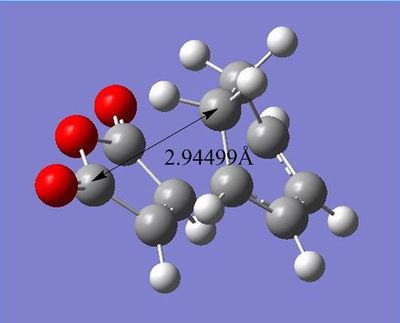
Through-space distances for endo were 3.89661Å, significantly larger than exo's 2.94499Å (This is not what your figure says. In any case, shouldn't the steric hindrance be more significant with respect to the H atoms? João (talk) 13:16, 23 December 2014 (UTC)). This demonstrates the endo transition structure's sterically strained state due to hindrance between groups.
Even though it is true that the endo TS has more steric strain (Didn't you just say the opposite? Are you talking about products? João (talk) 13:16, 23 December 2014 (UTC)), endo is the kinetic product. It is formed the fastest. The relative energies of the exo and endo transition structures are 90.915 kcal/mol and 90.163 kcal/mol, using the values from the electronic and thermal energies.
The activation energies of this DA reaction was calculated by this method of semi-empirical/AM1. The value obtained was 28.46kcal/mol for exo and 27.70kcal/mol for endo. These are significantly higher than the literature value of 11.4kcal/mol 8.
The relative values between the endo and exo transition states show that endo must be lower in energy in the energy profile diagram- it has a low activation energy compared to the exo, and is also lower in energy than the exo. This must be due to the existence of secondary orbital overlaps which cause a favorable orbital overlap between groups in the endo TS, thus lowering it in energy. The relative energies between the two conformers correspond to what would be expected in organic chemistry.
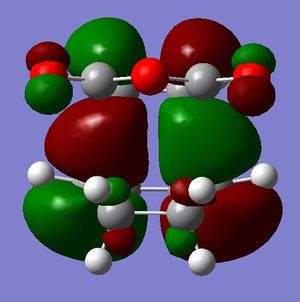
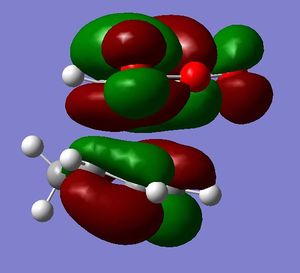
Below are pictures of the HOMO and LUMO orbitals of both endo and exo transition structures.
| Endo TS | Exo TS |
|---|---|
 |
 |
| Endo TS HOMO antisymmetric wrt plane | Exo TS HOMO, antisymmetric wrt plane |
 |
 |
| Endo TS HOMO, side view | Exo TS HOMO, side view |
 |
 |
| Endo TS LUMO, antisymmetric wrt plane | Exo TS LUMO, antisymmetric wrt plane |
 |
 |
| Endo TS LUMO | Exo TS, side view |
The HOMO orbitals of the endo transition structure should, according to organic chemistry and theory, display secondary orbital overlaps between the carbonyl carbons on the maleic anhydride and the opposite C=C bond on the diene backbone. However, clearly the MO diagram of the HOMO calculated using AM1 show no such orbital interactions.
Another method was used, that of DFT using B3LYP/6-31G* basis set. The activation energies calculated using this method gave 18.467kcal/mol and 15.850kcal/mol for exo and endo respectively. These values are much closer to the literature values 8. The energies and geometric properties are described in the tables below:
|
| ||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||
| ' | ' |
The table below shows the orbitals produced from DFT calculations. They are slightly different from the AM1 optimized orbitals.
| Endo TS | Exo TS |
|---|---|
 |
 |
| Endo TS HOMO antisymmetric wrt plane | Exo TS HOMO, antisymmetric wrt plane |
 |
 |
| Endo TS HOMO, side view | Exo TS HOMO, side view |
 |
|
| Endo TS LUMO, antisymmetric wrt plane | Exo TS LUMO, antisymmetric wrt plane |
 |
|
| Endo TS LUMO side view | Exo TS LUMO, side view |
Conclusion
This report explored different transition structures, ways to construct them, methods to optimise and locate them, and ways to compare different methods of theory for an overview of which method gives a result closer to experimental values. The Cope rearrangement was investigated, and this showed that the chair transition structure was the lower state, so favourable formation of products go via the chair transition structure. B3LYP/6-31G* gave more reliable results since it takes into account polarisation and electron correlation, which the HF/3-21G method did not.
A prototypical Diels Alder reaction was investigated, and results using AM1 were within reasonable comparison to literature values.
Diels Alder was also investigated. From this experiment, the results confirm that the endo transition state in a reaction between maleic anhydride and cyclohexa-,3-diene is lower in energy, and has a lower activation energy, due to secondary orbital interactions (What about steric effects? João (talk) 13:16, 23 December 2014 (UTC)). However, these interactions were not seen with AM1 or DFT methods used. These calculations could be carried out using other methods and larger basis sets to see if these orbital interactions can be located.
References
1. W. E. Doering., W. R. Roth., Tetrahedron., 1993., 18., 67-74
2. D. Rowley., H. Steiner., Discuss. Faraday Soc., 1951., 10., 198-213., DOI: 10.1039/DF9511000198
3. B. G. Rocque., J. M. Gonzales., H. F. Schaefer., Molecular Physics., 2002., 4(10)., 441-446
4. A. Bondi., The Journal of Physical Chemistry., 1964 3(10)
5. H. Lischka., E. Ventura., M. Dallos., ChemPhysChem., 2004., 5., 1365-1371 DOI: 10.1002/cphc.200400104
6. A. L. Magalhães., J. Chem. Educ., 2014., DOI: 10.1021/ed500437a
7. S. Aragorn., San Fransisco State University., Density Functional Theory.
8. C. A. Eckert., R. A. Grieger., J. Am. Chem. Soc., 1970, 92 (24), 7149–7153
9. J. J. Gajewski., K. B. Peterson., J. R. Kagel., J. Am. Chem., 1987, 109, 5545-5546
10. B. W. Gung., Z. Zhu., R. A. Fouch., J. Am. Soc., 1995, 117, 1783-1788
11. M. J. Bearpark, A. Simperler, 'Lectrure 3: Calculating Energies: Methods/Basis Sets/Spin States', QM3 Quantum Mechanics 3/Core 3rd Year Computational Chemistry Laboratory, 21/10/2014, Imperial College London
12. Table of Characteristic IR Absorptions, http://orgchem.colorado.edu/Spectroscopy/specttutor/irchart.pdf.
13. Locating Transition States, http://www.gaussian.com/g_whitepap/qst2.htm
14. Diels Alder Reactions, web.mit.edu/5.32/www/Appendix_1_Diels_Alder_Reactions_03.pdf.
15. 11. M. J. Bearpark, A. Simperler, 'Lectrure 1: Calculating Molecular Geometries', QM3 Quantum Mechanics 3/Core 3rd Year Computational Chemistry Laboratory, 14/10/2014, Imperial College London
16. Transition States, http://web.chem.ucsb.edu/~kalju/chem126/public/qm_ts_optim.html
17. Imperial Chemistry Wiki, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3