Rep:Mod:phys3pn813

Cope Rearrangement

Optimising Reactants and Products

---

The Cope Rearrangement is an organic pericyclic reaction which involves a [3,3]-sigmatropic rearrangement. In this reaction a sigma bond is broken and another one formed so that it appears to move from one position to another, so that Δσ=0.

Example of Cope Rearrangement

The Cope Rearrangement will be studied on the example of the 1,5-hexadiene molecule. This molecule can adopt several conformers, due to the possibility of free rotation around the Carbon-Carbon single bond, of which the energies will be calculated. Moreover the geometries and energies of the transition state will be studied.

The conformers 1,5-hexadiene can adopt are called anti- and gauche- conformers, which will be studied on several levels of theory, including HF/3-21G and DFT/B3LYP/6-31G*. It will be examined, which conformer is the one with the lowest energy, and therefore the most stable one. The sigmatropic rearrangement can occur via two possible transition states - the chair and boat transition state - and from the calculated energies from the transition state it will be decided, through which transition state the reaction is likely to go through.

Optimising 1,5-hexadiene Antiperiplanar conformer

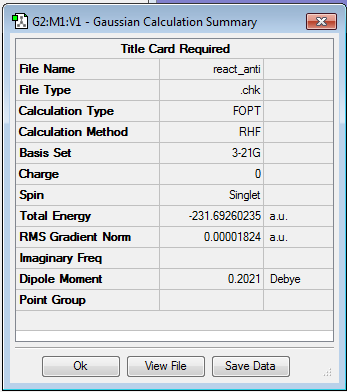
In the first part of the tutorial the anti-conformer of the molecule is drawn and optimised using GaussView 5.0. Thinking about the Newman projection the two double bonds need to be furthest apart, which therefore means on GaussView to change the dihedral angle to 180°, giving the maximum possible separation. The structure was then cleaned (Edit → Clean) and symmetrized (Edit → Symmetrize) to obtain the correct point group. The first optimization was run using the Hartree-Fock 3-21G level. What does GaussView do when calculating under a certain level or program? It translates the drawn molecule into a list of included atoms with their coordinates on a x,y,z-coordinate system and keeping the nuclei fixed (→ Born-Oppenheimer Approximation) it will attempt to solve the single electron Schrődinger equation, which will give the total energy of the molecule.

Nf710 (talk) 22:08, 4 November 2015 (UTC) This is only true for HF for DFT the hamaltonian is made of of functions that relate to the electron density and also electronic position, hence density functional theory. HF solves the many electron wave function by taking a slater determinant pf all the elctrons hence can be costly in large basis sets.

                                                                                                    $E\mathrm{\Psi }=\hat{H}\mathrm{\Psi }$

To obtain the energy the right side of the equation needs to be solved. The Hamiltonian, which is the method, is the level of theory that GaussView is told to use for the calculation (e.g. Semi-Empirical, Hartree-Fock or Density Functional Theory), whereas the wavefunction is being described by the basis set (e.g. STO-3G or 6-31G*).

Hartree-Fock method is used for this calculation, since 1,5-hexadiene is a relatively small molecule and therefore the method can used, which does not make any assumptions and should therefore give the most exact result. The energy was found to be -231.69260235 a.u. and the point group was determined to be C_{2 .}

The energy is a negative value due to the method with which Gaussian calculates it. For calculating the energy Gaussian first assumes that all atoms in the molecule are infinitely far apart and calculates their energy and sets it to 0. Then it compares it to the actual structure in which the nuclei-electron stabilisation is much larger than any repulsion, which makes it more energetically favourable than the infinite separation, which results in a negative value .

Nf710 (talk) 22:14, 4 November 2015 (UTC) Good understanding of how potentials work.

The Optimisation log file can be found here

Optimised antiperiplanar structure	Summary	Point Group
HF/3-21G optimised 1,5-hexadiene antiperiplanar		C2

Optimising 1,5-hexadiene Gauche conformer

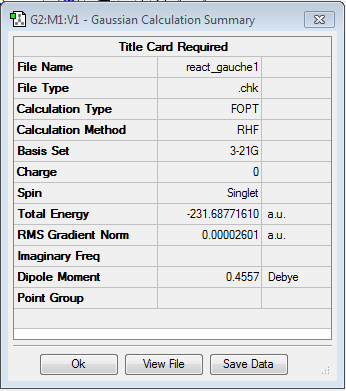
After optimising the anti-conformer one gauche conformer of 1,5-hexadiene was drawn and optimised using the same HF/3-21G level of theory. In order to draw it the dihedral angle between the two terminal double bonds was changed to 60° and the structure cleaned and symmetrized. Here the energy was found to be -231.68771610 a.u. but the point group is the same (C₂)

The Optimisation log file can be found here

Optimised gauche structure	Summary	Point Group
HF/3-21G optimised 1,5-hexadiene gauche		C2

It can be seen that between the two conformers differ in energy. As expected the anti conformer has a lower energy than the gauche conformer. This is due to reduced steric clashes between the two ends of the molecule and improved hyperconjugation leading to electronic stabilisation - therefore an lower energy conformation. In the gauche conformation the two ends of the molecule are as close together as possible; therefore significantly raising its energy.

Both conformers optimised were compared with the structures given in the Appendix 1 and were found to correspond to the Anti1 and Gauche1 conformers respectively . The energies matched up to the last digit of precision given in the Appendix and it can be therefore said that the optimisation worked.

Optimising 1,5-hexadiene lowest energy conformer

In the 1,5-hexadiene molecule 3 freely rotating Carbon-Carbon single bonds exist and 3 rotational minima around each of these bonds which in total leads to 27 theoretical structures of this molecule. However, in previous research it was shown that only 10 of them are energetically different. Therefore it needs to be further investigated if there is a structure of 1,5-hexadiene with a lower energy than the Anti1 form drawn and shown earlier. Therefore another conformer was drawn that was somewhere in the middle between the Anti1 and Gauche1 conformer.

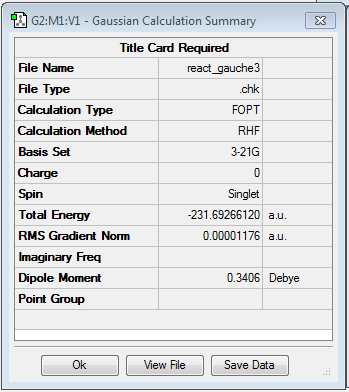
The point group was found to be C₁1 and the conformer has an energy of -231.69266120 a.u.

The Optimisation log file can be found here

Optimised structure	Summary	Point Group
HF/3-21G optimised 1,5-hexadiene		C1

Comparing this to the 10 energetically different structures found in the Appendix this turns out to be the Gauche3 structure, which with a relative energy of 0.00 kcal/mol is the lowest energy conformer. It is worth noticing that the lowest energy conformer is not an anti structure as would be expected from the earlier explanation but is actually a Gauche conformer. The a.u. energy differences between the lowest energy conformer and the anti1 conformer optimised first is very low on this level of optimisation. It is suggested that this is due to Hartree-Fock method used. Hartree-Fock methods do not include any electronic correlations which hinders electronic effects like π-CH interactions from being considered However an attempt of explaining could be that in this conformation the terminal double bonds are far enough apart to prevent steric clashes between the terminal hydrogens which could lead to a raise in energy; but the ends are close enough together to lead to a good and favourable orbital overlap between the π-orbitals on carbons 2 & 4. This leads to a slightly delocalised π-electron cloud which lowers the energy of the conformer. The orbital shown is the HOMO, which means that it is actually occupied so that electron delocalisation can occur.

HOMO of the lowest energy conformer of 1,5-hexadiene

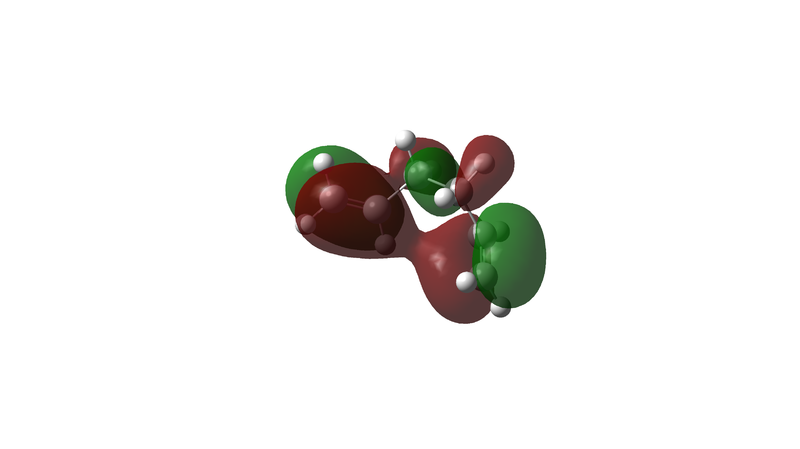
Nf710 (talk) 22:22, 4 November 2015 (UTC) It is very good how you have gone beyond the script here to demonstrate how the secondary orbital interactions are responsible for lowing the energy of the gauche3 conf. this is exactly the type of situation we would use to solve a problem like this by visualizing the orbitals. However if you look in the reference that you have quoted they run it with a basis set of 631G. Si the level of theory is not responsible for this energy it is just the orbital interactions.

Optimising 1,5-hexadiene Anti2 conformer

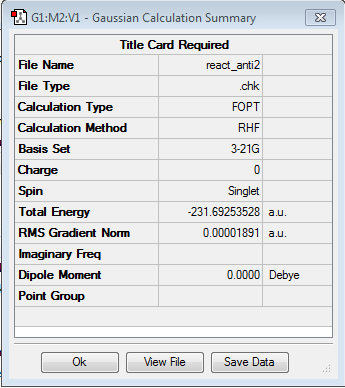
In the next part of the Cope Rearrangement tutorial the Anti2 conformer will be drawn and optimised. Also here the HF/3-21G method will be used for optimisation. It was tried to guess the structure as well as possible from the image found in the appendix.

The energy for this conformer was found to be -231.69253528 a.u. which agreed with the value given in the Appendix to the certainty that it is given in the Appendix. Whilst there are only 5 decimal places given in the Appendix (-231.69254 a.u.) the result calculated was a bit more exact; however if it is rounded to the 5^th decimal place the results match. The point group was established to be C_i.

The log file for this optimisation can be found here

Optimised structure	Summary	Point Group
HF/3-21G optimised 1,5-hexadiene Anti2		Ci

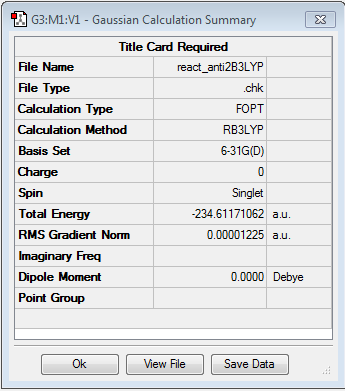
Reoptimising 1,5-hexadiene Anti2 conformer using the Density Function Theory

As mentioned before the Hartree-Fock method does not make any assumptions and does not take any electron correlations into account, which makes it a method to quickly calculate and optimise molecules; however does not give the most precise results. In order to take electron correlations into account, another method, namely Density Function Theory [DFT], is used. The wavefunction of Schrődinger's equation is also described by a higher level of theory using B3LYP/6-31G*.

Nf710 (talk) 22:37, 4 November 2015 (UTC) HF treats the electronic interaction a mean field, which is normally over estimated. DFT takes into account exchange correlation which is the interaction between electrons put simpily.

The log file for this optimisation can be found here

Optimised structure	Summary	Point Group
DFT/6-31G* optimised 1,5-hexadiene Anti2		Ci

After the optimisation on this level of theory the energy was checked and it was noticed that it was different from the result obtained before with the Hartree-Fock method. However, these energies are only relative energy values instead of absolute ones; so comparing them across different levels of theories does not make sense. However what can be compared is the optimised structure in terms of bond lengths, bond angles and point group.

Labelled atoms on Anti2 Conformer of 1,5-hexadiene

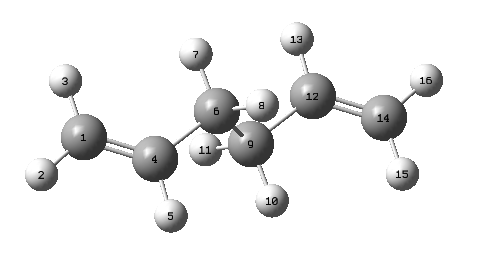
1,5-hexadiene	Bond length (Å)					Bond Angle (°)			Point Group
	C1-C4	C4-C6	C6-C9	C9-C12	C12-C14	C1-C4-C6-C9	C4-C6-C9-C12	C6-C9-C12-C14
HF/3-21G	1.31613	1.50891	1.55275	1.50891	1.31613	-114.66880	180.00000	114.66880	Ci
DFT/B3LYP/6-31G*	1.33356	1.50417	1.54806	1.50417	1.33356	-118.59280	180.00000	118.59280	Ci

From this table it can be seen that the differences in bond angles and bond lengths differ slightly but not significantly. The point groups however, are identical and therefore it can be said that the geometries do not differ.

Nf710 (talk) 22:40, 4 November 2015 (UTC) The geometries do change as the bond angles change and therefore the cartesian coords change. but they change on both sides of the center of inversion equally and there the pont group does not change.

Frequency Analysis at 298.15 K

The energy values that were calculated in the optimisations are relative energy values and cannot be compared to experimental data. In order to do this a frequency calculation was run; which will calculate additional terms to derive absolute values, which are comparable. This frequency calculation was conducted using the DFT B3LYP/6-31G* basis set as well and used the optimisation output file as the input file. The thermodynamic data obtained from the log file is summarised below:

Thermodynamic Property	Result	Unit
Sum of electronic and zero-point energies	-234.469215	a.u.
Sum of electronic and thermal energies	-234.461867	a.u.
Sum of electronic and thermal enthalpies	-234.460922	a.u.
Sum of electronic and thermal free energies	-234.500800	a.u.

The electronic and zero-point energies are calculated at 0K, whereas the the electronic and thermal energies are calculated at 298.150 K and 1.000 atm. At 298.150 K and 1.000 atm the energy is slightly different because now the molecule is not 'frozen' anymore and therefore contains vibrational, rotational and translational contributions to the energy, altering it. The thermal enthalpy is calculated using H=E+RT, where H=Thermal Enthalpy, E=Thermal Energy, R=Ideal Gas Constant and T=Temperature in Kelvin. For the zero point energy the enthalpy would be equal, since at 0 K the RT term would be 0 too. However, at 298.150 K this term becomes significant and therefore the thermal enthalpy is slightly higher, which agrees with the equation. Using this equation constant pressure is assumed. The sum of electronic and thermal free energies is different in the way that now the entropic contribution becomes significant too. Talking about free energies the following equation needs to be used: G=H-TS, which assumes constant pressure too. Since T= 298.150 K the TS term becomes large and positive and therefore the thermal free energy term is smaller than the other terms. In order to use the equation G=H-TS one needs to know the entropy of the system, which is most likely determined using the partition function . In order to confirm if a minimum was calculated the and optimised the Vibrations in the results section were checked. The calculated IR spectrum can be seen below:

Calculated frequencies for the optimised Anti2 conformation

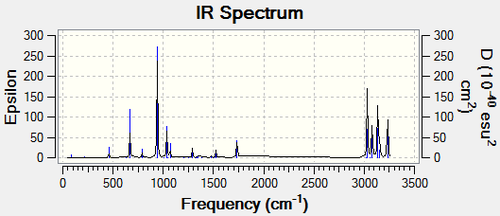
It can be seen that all the calculated frequencies are positive, which means that a minimum was calculated rather than a transition state, in which a negative frequency would be present. From the major peaks present one can also try and assign these to specific stretches/vibrations. There is one major peak at around 900 cm^-1, which corresponds to the terminal CH₂ wag. The stretches between 3000 and 3200 cm^-1 could correspond to Carbon-Carbon stretches of sp² and sp³ hybridised carbons. Since the sp² hybridised carbons are bound by a stronger double bond than the sp³ hybridised ones (bound by a single bond) these require more energy to be set into stretches than the single bonds and are therefore found at higher frequencies.

Nf710 (talk) 22:58, 4 November 2015 (UTC) You have calculated the thermochemistry correctly and you have show a very good understanding here. Good understanding of how the partition function is used to calculate the entropy.When we say we are doing a frequency analysis we are typically not that interest in the various CH streches, these are all calculated from localising the hydrogens and calculating the intensity from group theory. We typically just do it show it is at a minimum.

Optimising "Chair" and "Boat" Transition Structures

---

Optimising Chair Transition structures

The first task was to draw an allyl fragment (CH₂CHCH₂) on GaussView and optimise it using HF/3-21G level. The resulting structure from the checkpoint file was copied and pasted into a new empty GaussView sheet and oriented so that the two fragments would already resemble a chair transition state. For this the terminal carbons were separated by 2.2 Å. Then a Hartree-Fock frequency+optimisation was run using the TS(Berny) method. The keyword opt=noeigen was added which stops the program from crashing in case 2 or more imaginary frequencies are found. Finding a transition state is harder than finding the minimum of a structure because during the calculation the negative direction of the curvature needs to be found. Therefore it is important that the input structure resembles the guessed transition structure as much as possible.

Nf710 (talk) 23:04, 4 November 2015 (UTC) you should should show some understanding that the second differential of the PES relates to the force constant which then relates the k in the QM representation of a vibronic oscilator which has the term (k/m)^1/2 therefore a TS would give a imaginary frequency.

The log file can be found here

Optimised structure	Summary	Frequencies
HF/TS(Berny) optimised chair TS state

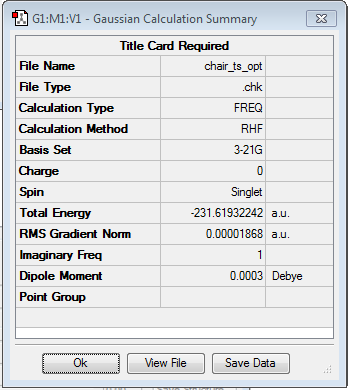
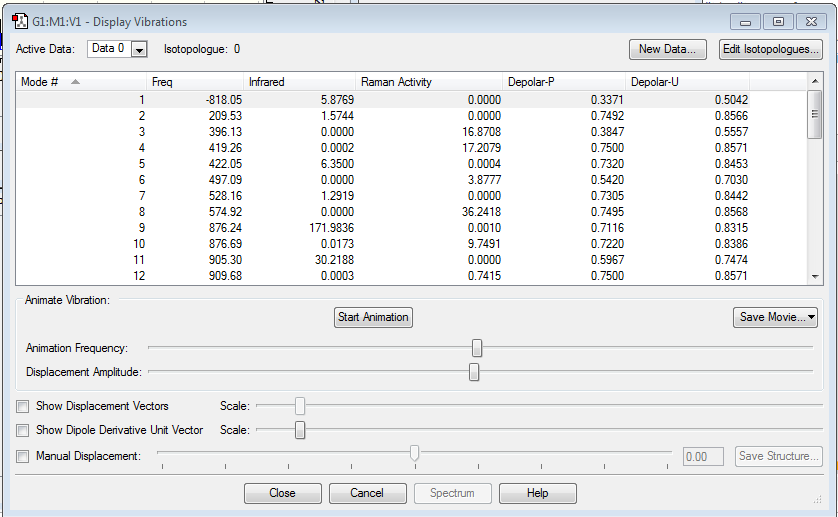
From the frequency chart it can be seen that there is one imaginary frequency with -818.05 cm^-1 which confirms, that the transition state was actually found. The table of frequencies is shown instead of the IR spectrum because the IR spectrum is not obtainable since it is a transition state and therefore would not be realisable. However, the motion that the molecule goes through during the transition state can be shown nicely:

Chair Transition State Movement

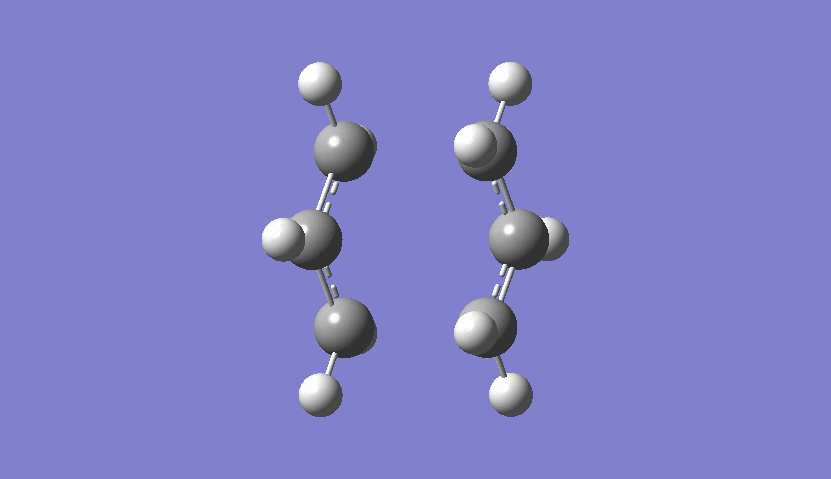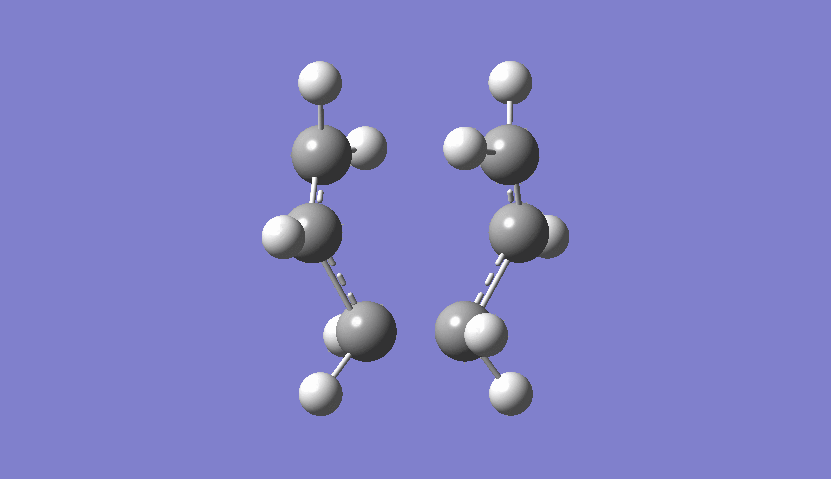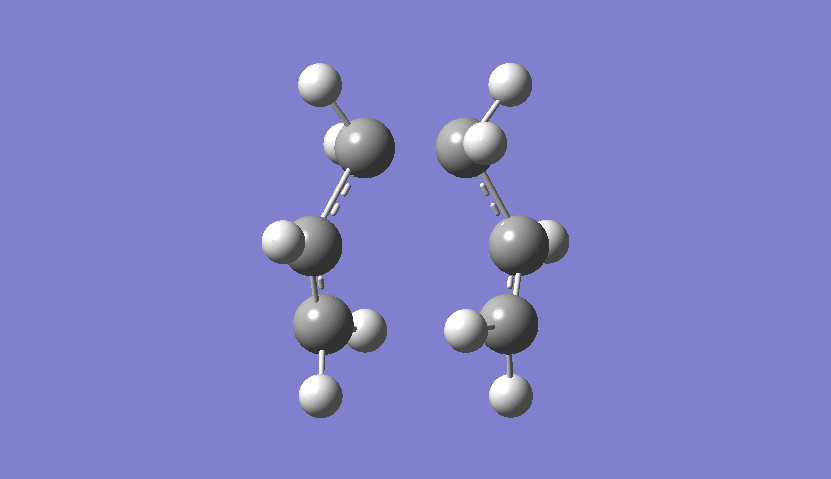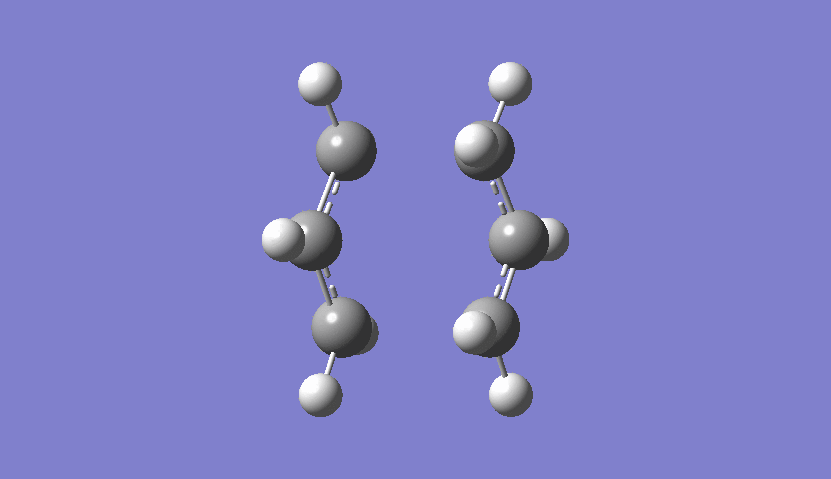
Optimisation of the Chair Transition State using the Frozen Coordinate Method

Again the guessed structure for the transition state is pasted into a new sheet. However, this time, rather than guessing it completely, the redundant coordinate editor is used. Using this editor the distance between the terminal carbon atoms on both parts were frozen to about 2.1 Å. The transition state was then found using Hartree-Fock TS(Berny) method.

The log file for this can be seen here

Optimised structure	Summary	Frequencies
HF/TS(Berny) optimised chair TS state FCM

Also here one can see from the frequency chart that one imaginary frequency has been calculated (-817.89 cm^-1) so that it is certain that the transition state has been calculated. The motion of this imaginary frequency is viewed here:

Chair Transition State Movement FCM

Comparing the frequencies and motions during the transition state it can be said that the two optimised outputs resemble each other strongly. A comparison of the bond angles will give more insight into how close the results of the two different methods are.

	Terminal Carbons 1	Terminal Carbons 3
TS method 1	2.02024
TS method 2 (FCM)	2.02074	2.02072

It can be seen that the differences between the terminal carbon distances are very small so that it can be concluded that these two different methods of finding the transition state give equal results.

Optimising the Boat Transition Structure

Other than the chair transition structure the transition could also occur through the boat transition structure. In order to do this another method is being used, which is called QST2. In this method one can specify the reactants and also the products of a reaction and the calculation interpolates between them, trying to locate the transition state the reaction needs to go through. Since 1,5-hexadiene is used as an example and the product equals the reagent after the cope rearrangement the atom labelling needs to be edited. The following labelling was used and the optimisation was run.

Labeling of Reactant and Product Molecule for QST2

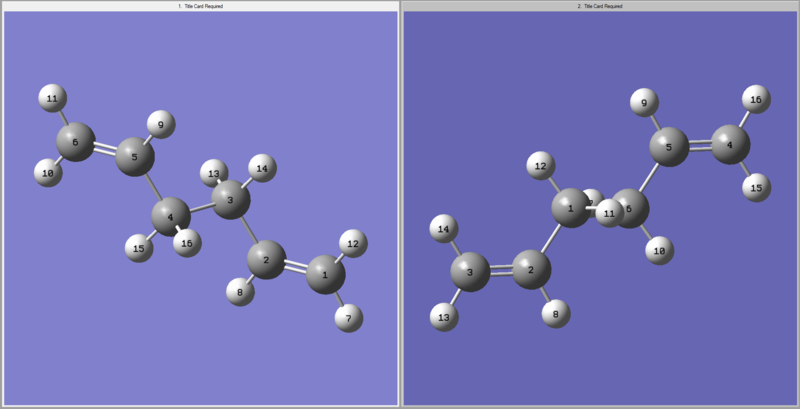
The following result for the transition structure optimisation is obtained (log file here )

Optimised structure
First obtained TS structure

This is clearly not the desired transition structure, since it is not a boat transition structure. In order to obtain the actual boat transition structure the angles between the carbons in both the product and the reagent were changed.

	C2-C3-C4-C5	C2-C3-C4	C3-C4-C5
Angle (°)	0	100	100

The QST2 input and output files looked like this:

Optimisation Input (Reactant and Product)	Optimised Boat Transition State
	First obtained TS structure

It can be seen that the input with the modified angles lead to the correct boat transition structure ( log file ) , which is also shown. The imaginary frequency vibration is shown below, which indicates that the transition state was found.

Now the transition structures for the chair and boat transition states are examined, and specifically the vibrational modes arising from the imaginary frequency. From here is impossible to which conformer they will go through after the transition state. Since there are so many different conformations (27 or 10 energetically different ones) one cannot predict from here to which it will proceed because simply not enough data is available from looking at the transition state vibration.

Nf710 (talk) 23:11, 4 November 2015 (UTC) You havent checked what the imaginary frequency is for the TS

Intrinsic Reaction Coordinate

As mentioned before it cannot be properly predicted from the transition state vibration which product it will proceed to. In order to find out, GaussView has an integrated method, IRC, which finds the minimum energy path to lead to a local minimum. It does that by taking small geometry steps in the direction with the deepest energy slope and therefore finds the final product structure.

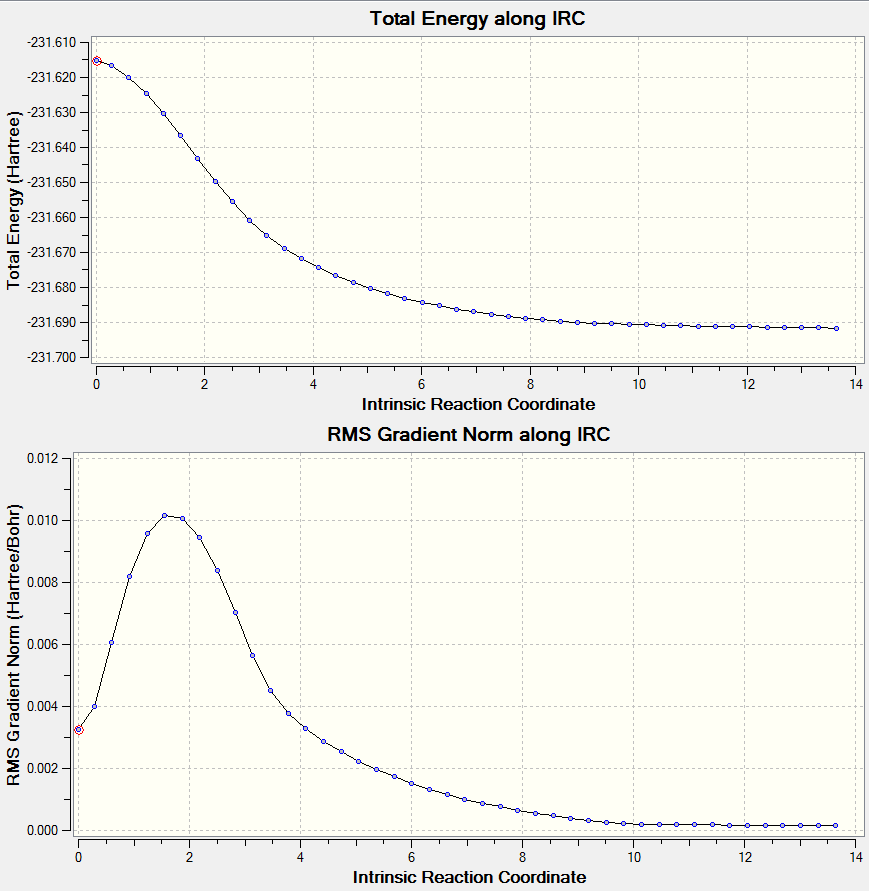
This is firstly demonstrated by running an IRC for the chair transition state. The input file is simply the optimised transition state structure for the chair (it does not matter via which method the TS was derived). (log file here )

IRC 50 Steps	Reaction Path

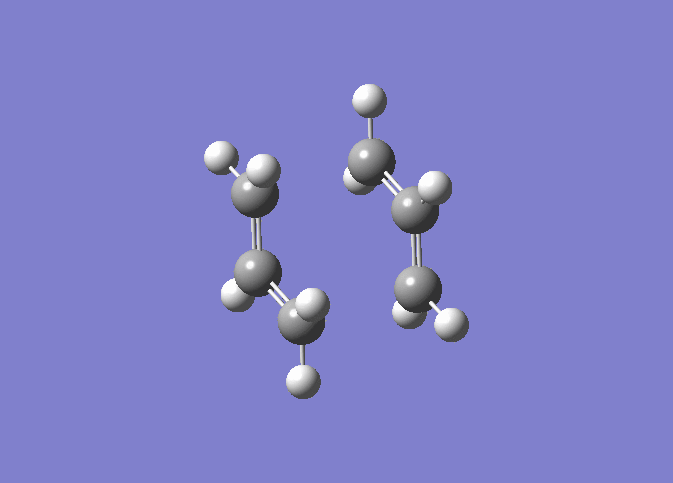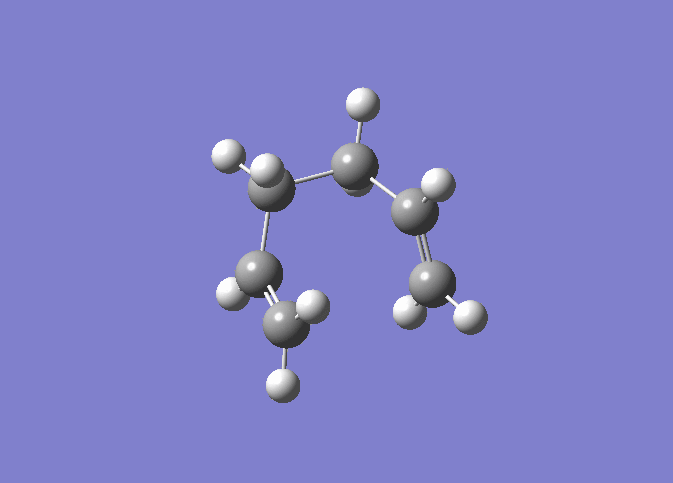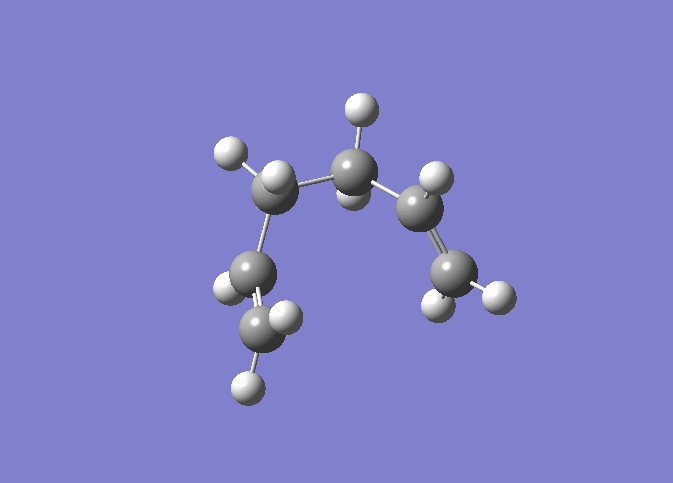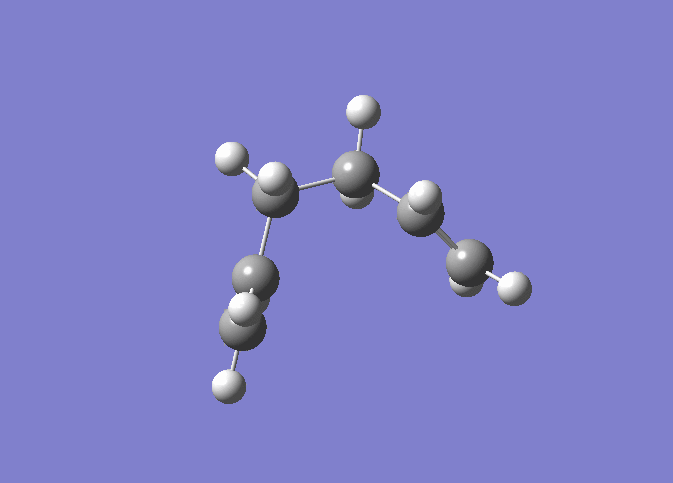
The IRC was run on 50 steps first, for which the reaction coordinate is shown. The IRC stopped after 44 points, which meant that a local minimum on the potential energy surface was found. The reaction is also shown and it can be nicely seen how the reaction proceeds through the transition state through to the final product. It was confirmed that point 44 on the reaction coordinate is actually a minimum since the IRC was run again with 70 steps (log file here ) on the input which also stopped after 44 points. After that the last point found in the IRC (the apparent minimum) was minimised in energy using the HF/3-21G method in order to see how close the IRC got to the actual energy of this structure. (log file here )

The summary can be seen here:

Summary Minimisation

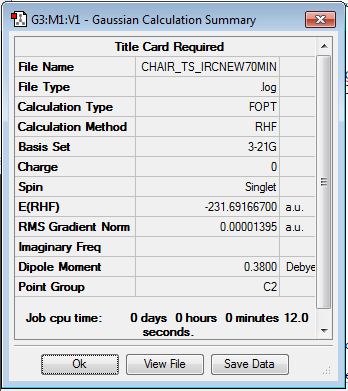
After the minimisation the energy of the structure was -231.69166700 a.u.; whereas in the IRC the energy of structure 44 is -231.692. Therefore it can be said that the structure found in the IRC is already really close to the minimised structure. Since there are only 3 decimal places available it is not known how much they differ in energy; but it must be small, since rounding the other value results the same value. The point group was found to be C₂. The local minimum therefore corresponds to the gauche2 conformer, since both point group and energy match the information given in the Appendix.

Nf710 (talk) 23:15, 4 November 2015 (UTC)There is no need to do 70 steps if you look in the log file you should be able to see that the gradient will converge to 0

Activation Energies

In order to investigate through which transition state the Cope rearrangement is likely to proceed the activation energies need to be calculated. In order to do this both transition structures will be reoptimised using a higher level of theory to obtain more precise results. The 6-31G* method in B3LYP is used to carry out the optimisation to a transitoin state (TS Berny). The input file was the already optimised structure from the HF/3-21G calculations. In the keywords opt=noeigen was added to prevent the calculations from crashing again.

Firstly the results for the chair transition state are shown (log file here ): The point group was found to be C_2h and the energy found to be -234.55693156 a.u. so that both properties are in close agreement with the information given in Appendix 2 and 3. The imaginary frequency was found at -569.34 cm^-1

Chair Imaginary Frequency	Chair Transition Structure	Summary
	Obtained Chair TS Structure

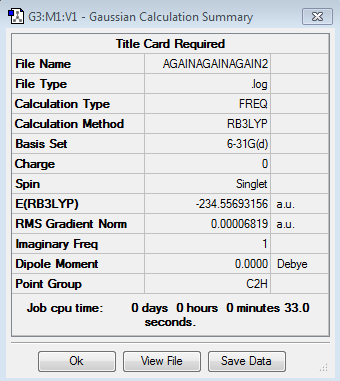
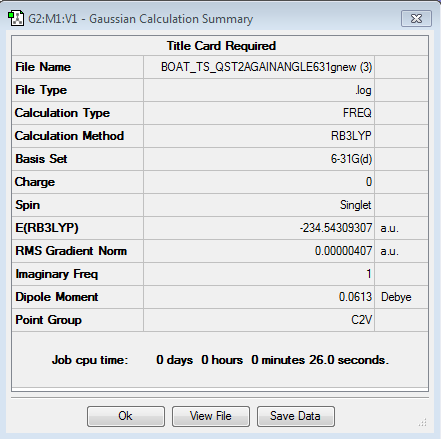
Then the boat transition structure was re-optimised using the higher level of theory too. (log file here ): The point group was found to be C_2v and the energy of the transition state is -234.54309307 a.u.. Also this is in very tight agreement with the values obtained in the Appendix 2 and 3. The imaginary frequency for which the vibration is shown was calculated at -530.36 cm^-1.

Boat Imaginary Frequency	Boat Transition Structure	Summary
	Obtained Boat TS Structure

These structures that were obtained using DFT/B3LYP/6-31G* (high level of theory) can now be compared to what was obtained with the HF/3-21G level of theory in order to see, how much difference more computational time makes. Both, energies and structure/geometries are being compared.

Geometries

Method	C1-C1 Chair TS	C3-C3 Chair TS	C1-C1 Boat TS	C3-C3 Boat TS
HF/3-21G	2.02024	2.02012	2.13998	2.13999
DFT/B3LYP/6-31G*	1.96988	1.96988	2.20664	2.20664

From the images for the optimised structures it can be said that the geometries optimised look very similar. Furthermore the distances between the allyl fragments were being compared. It can be seen that there seems to be the trend that the lower accuracy method (HF/3-21G) seems to underestimate the distance between the ends. The distances calculated with the higher accuracy method is always slightly higher, but nevertheless there is no immense difference. It can be said that overall the geometries were calculated equally well with both methods.

Comparison of the energies calculated

The following table is an overview of the energies obtained for the Boat TS, Chair TS and the Anti2 Conformation reagent. The overview consists of a comparison between the two levels of optimisation (HF/3-21G and DFT/B3LYP/6-31G*) and also between 0 K and 298.15 K. In order to obtain the pure electronic energy the zero-point correction value found in the log file was subtracted from the value for Sum of Electronic and Zero-point energies.

	HF/3-21G (Energy in hartree)			DFT/B3LYP/6-31G* (Energy in hartree)
	Electronic Energy	Sum of Electronic & Zero-Point Energy ( 0 K )	Sum of Electronic and Thermal Energy ( 298.15 K )	Electronic Energy	Sum of Electronic & Zero-Point Energy ( 0 K )	Sum of Electronic and Thermal Energy ( 298.15 K )
Chair TS State	-231.619304	-231.466697	-231.461338	-234.556934	-234.414886	-234.408956
Boat TS State	-231.602165	-231.450929	-231.445300	-234.543093	-234.402342	-234.396007
Anti2 Conformer Reactant	-231.692535	-231.539539	-231.532566	-234.611712	-234.469215	-234.461867

In the previous section it was concluded that the geometries obtained for either level were pretty much equal. Looking at the energies calculated a different picture shows. Between the results obtained for HF/3-21G and the B3LYP/6-31G* method a difference of about 3 hartree exists. In order to see, which method is closer to the experimentally obtained one, the activation energies need to be calculated and converted into kcal/mol (1 hartree = 627.509 kcal/mol). In order to calculate the activation energy for 0 K the difference between the energy of the reactant at 0 K and the TS at 0 K was found. In this method the Sum of Electronic & Zero-Point Energies is used because the experimental data for 0 K is given and at 0 K the molecule does need to be corrected from the electronic energy because even at 0 K it does have a fuzzy mix of some vibrations and rotations. The Sum of Electronic and Zero-Point Energy is the energy actually obtained by the molecule at 0 K and therefore this one is used. For 298.150 K the Sum of Electronic and Thermal Energy is used.

	HF/3-21G		DFT/B3LYP/6-31G*
	0 K	298.150 K	0 K	298.150 K
Chair TS Activation Energy (kcal/mol)	45.709	44.696	34.092	33.202
Boat TS Activation Energy (kcal/mol)	55.604	54.760	41.963	41.328

The experimental values obtained for this reaction at 0 K are 33.5 ± 0.5 kcal/mol for the Chair Transition State and 44.7 ± 2.0 kcal/mol for the Boat Transition Structure. First of all it can be concluded that since the Chair Transition has the lower activation energy this specific Cope rearrangement is likely to proceed via the Chair transition structure. Furthermore it is clear that the higher level of accuracy and precision of the B3LYP/6-31G* lead to results that are reasonably close to the experimentally determined ones. The value obtained for 0 K for the chair transition structure is within the uncertainty of the experimentally determined result. And also for the boat transition it is quite close to the lower end of result when the uncertainty is included. All in all it can be said that if the geometry of a molecule or transition state needs to be determined, the computationally cheaper and shorter methods can be used, but for energies it is worth spending more computational time to have results closer to the real experimentally determined values (Even though both methods agree that the chair transition state has a lower activation barrier to go through). The difference between the experimental and calculated value for the boat transition structure is higher than for the chair transition structure. This could be because the boat transition structure is higher in energy and therefore harder to obtain. The differences in both, the chair and boat activation energies, could be attributed to the lack of intermolecular forces during the calculation, which should make a difference, since they must have occurred during the real experiment.

Nf710 (talk) 23:26, 4 November 2015 (UTC) You have correctly deduced the activation energys and nicely compared them nicely. Also deducing that energy is much more dependant on basis set than geometry. In all a very good first section and your used of looking at the orbitals to find the second order oribital interactions was good. However you could have been a lot more concise with your report.

Diels-Alder Cycloaddition

Example of Diels-Alder Cycloaddition

The Diels-Alder cycloaddition is an organic [4+2] cycloaddition between a conjugated diene and another substituted alkene. In this type of reaction the two π C-C double bonds are broken and two σ C-C single bonds are formed, which is also the driving force for this process, since the energy released by the formation of σ bonds is higher than the energy cost of breaking two π bonds . This process of π bonds breaking and σ bonds forming happens simultaneously (concerted fashion) and via a cyclic transition state, which are the reasons for why this reaction is a cycloaddition. There are two different ways in which the Diels-Alder Cycloaddition can be set up - normal and inverse electron demand. In the normal electron demand the dienophile (alkene) contains an electronwithdrawing group, which makes the LUMO (lowest unoccupied molecular orbital) lower in energy and the diene contains electrondonating groups, which makes the HOMO (highes occupied molecular orbital) rise in energy. This therefore reduces the energy gap between the two interacting orbitals and therefore they can interact stronger. The inverse electron demand, as already given by the name, is when the dienophile contains the electrondonating groups; which makes the HOMO rise in energy. The diene will contain the electronwithdrawing groups, reducing the energy of its LUMO but giving the same result that the interacting orbitals are closer in energy and interact stronger.

A classical example for this type is the reaction between maleic anhydride (substituted alkene) and Cyclohexa-1,3-diene (conjugated diene).

Cis-butadiene

However, for the beginning cis-butadiene is drawn and optimised. For this optimisation the AM1 semi-empirical method is used. This method is based on the Hartree-Fock method, but is much faster, since it includes the Zero-Differential Overlap Approximation. The drawback is, however, that the computations can fail if the molecule drawn does not resemble any of the ones found in the database. It was drawn connecting two ethene molecules with a single bond and deleting the redundant hydrogen atoms. The dihedral angle was changed to 0.00° and the molecule was also symmetrized to a C_2v point group. The Optimisation log file can be found here.

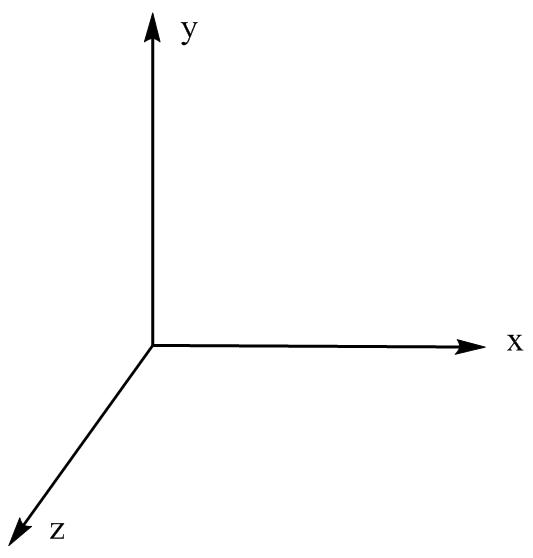
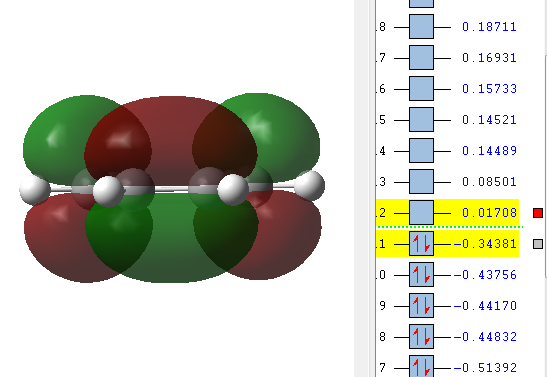
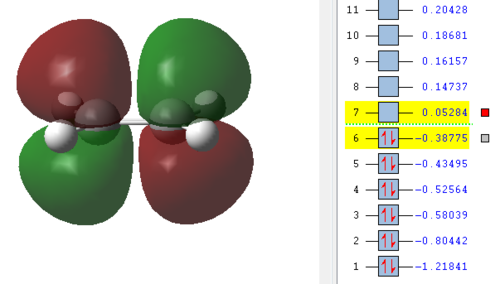
From the images it can be seen that the LUMO is a symmetric molecular orbital, whereas the HOMO is antisymmetric with respect to the yz-plane (as dranw on the set of axis)

Labelled Axis	LUMO of optimised cis-butadiene	HOMO of optimised cis-butadiene

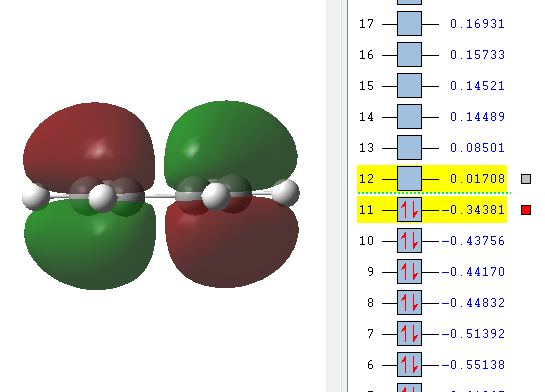
Study of the reaction between Cis-butadiene and ethene

This is used as a prototype reaction for the actual Diels-Alder reaction that needs to be studied. To the (previously optimised) cis-butadiene molecule an ethene molecule is added and the transition structure is guessed. It is known that the transition structure resembles an envelope structure. The reason for this is that in this way the overlap between the π-orbitals that are involved in the reaction is maximised. The 'structure' drawn was symmetrised to the C_s pointgroup and then optimised. It was optimised to a transition structure (TS Berny) with the previously mentioned AM1 semi-empirical method. The Optimisation log file can be found for Optimisation here, Frequency Analysis here & IRC here It can be confirmed that a transition state was found due to the presence of an imaginary frequency at -956.09 cm^-1. The energy of the optimised structure was found to be 0.11165465 a.u.

TS Summary	Diels-Alder Transition Structure	Imaginary Frequency
	TS Structure for Cis-butadiene and Ethene Diels-Alder Reaction

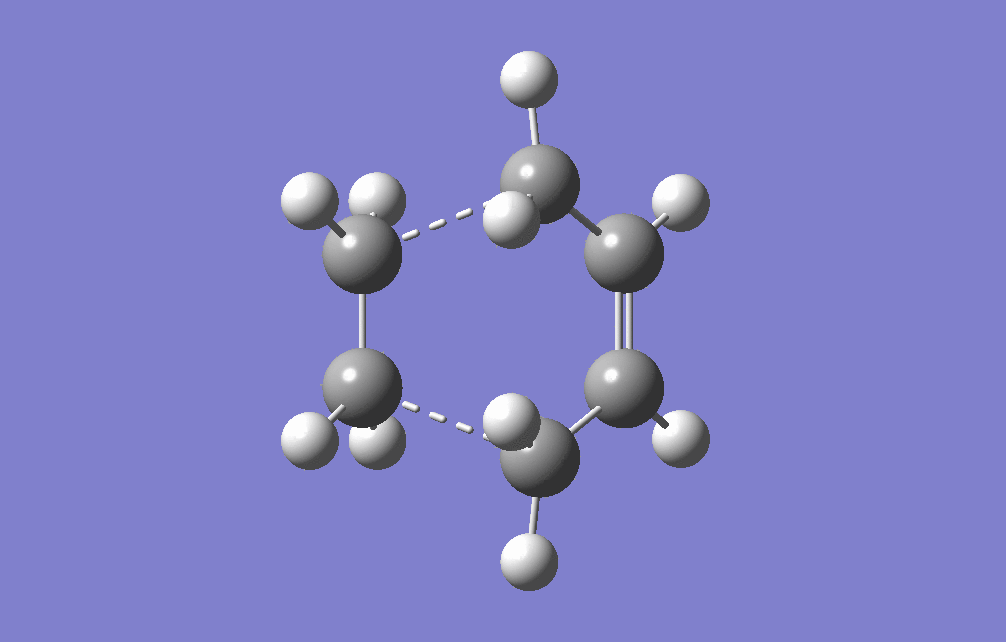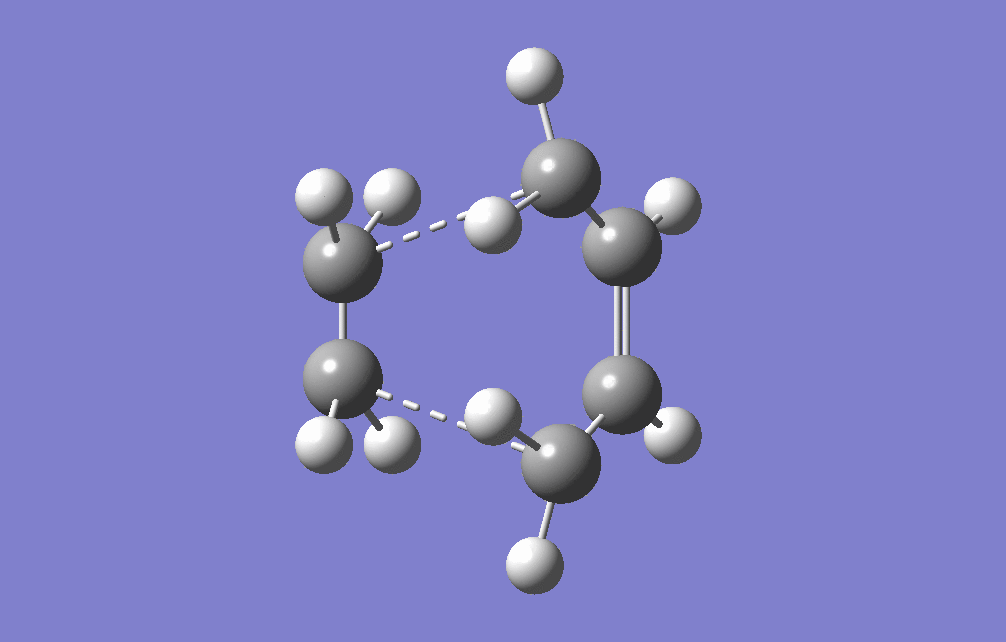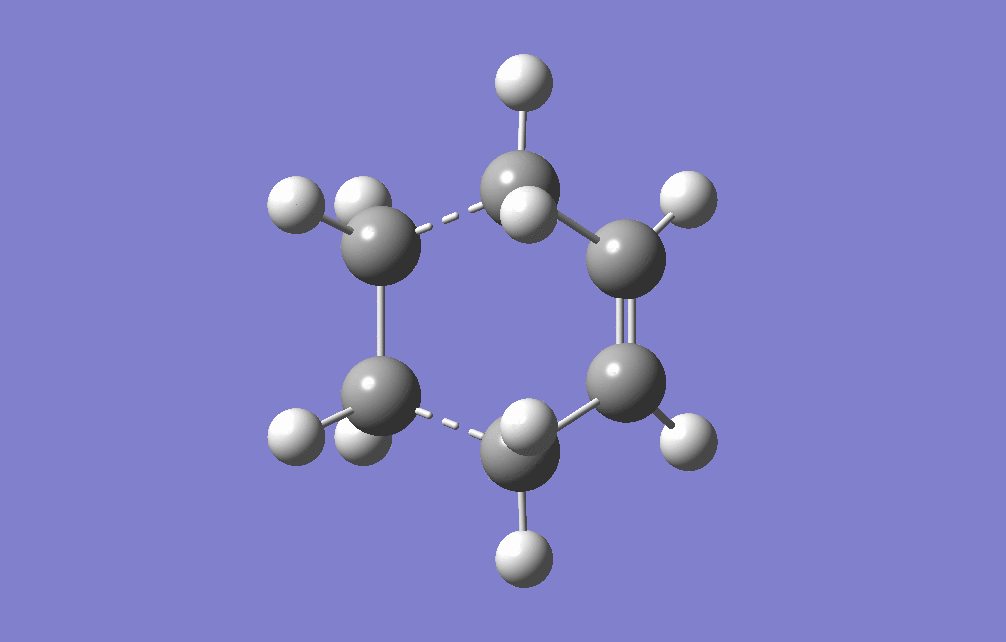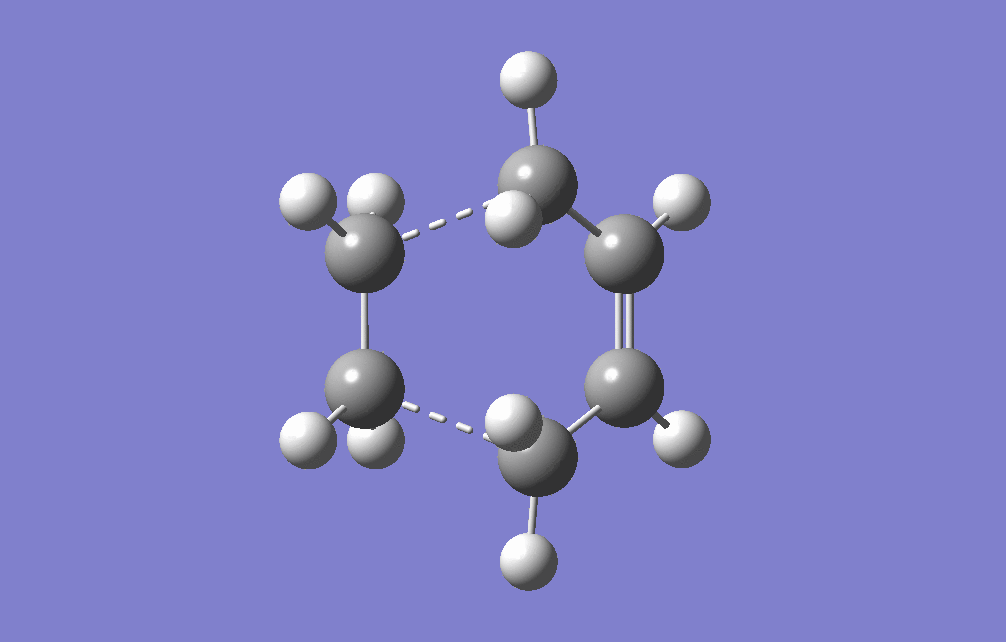
Furthermore the lowest positive/real vibrational frequency will be shown. The lowest real vibrational frequency was calculated to be at 147.21 cm^-1. This corresponds to an asynchronous vibration/wag of the transition structure.

Lowest real frequency

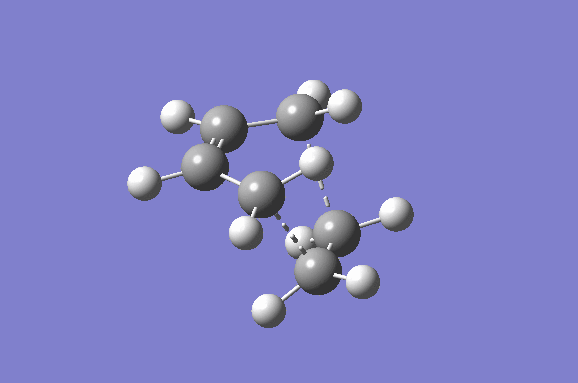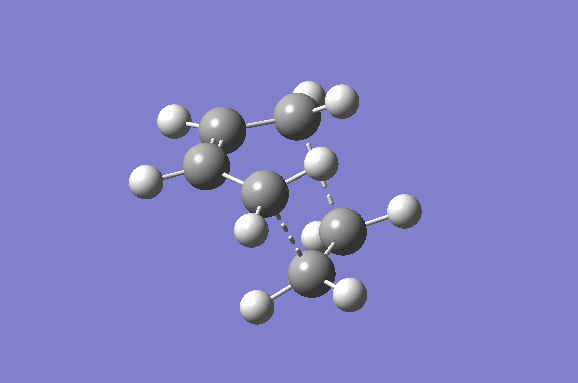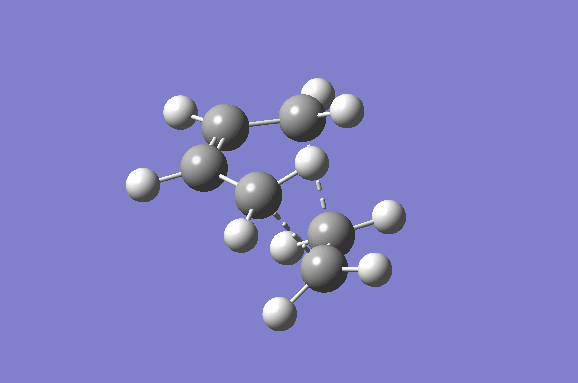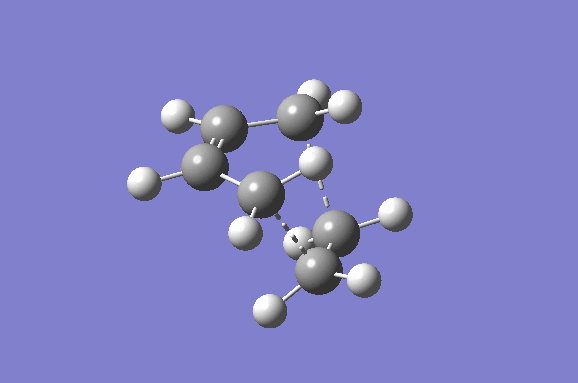
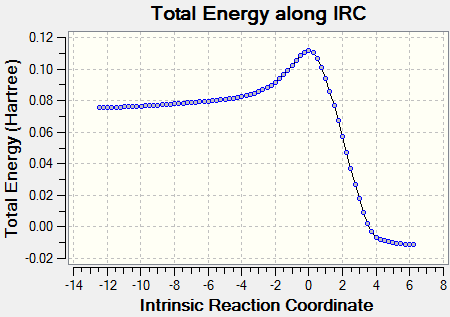
The movie shows that the bonds break and form in a concerted fashion. Also from the IRC path it can be seen that only one transition state is present during the cycloaddition which is shown by only one peak on the path. From this diagram it can also be seen that the transition state is very close in energy to the reactants, which makes it an early transition state according to Hammond's Postulate.

IRC	Reaction pathway

Now the orbitals need to be analysed. Especially important are the HOMO and LUMO orbitals of the reactants as described in the introduction. From here it can be seen if the reaction occurs with normal or inverse electron demand. Since this is a type of pericyclic reaction the Woodward-Hoffmann rules need to be followed to check if a reaction is allowed. According to this rule a reaction is allowed if the orbital symmetry of the reacting orbitals is preserved during the reaction. It can be seen that the HOMO of the dienophile is lower in energy than the HOMO of the diene and therefore it can be concluded that the reaction follows a normal electron demand. This means that the HOMO of ethene and the LUMO of cis-butadiene combine to form the LUMO of the transition state, since the symmetry needs to be preserved. Equally the LUMO of ethene and HOMO of cis-butadiene combine to form the antisymmetric HOMO of the transition state.

Ethene	Cis-butadiene	Transition Structure
HOMO symmetric LUMO antisymmetric	HOMO antisymmetric LUMO symmetric	HOMO antisymmetric LUMO symmetric

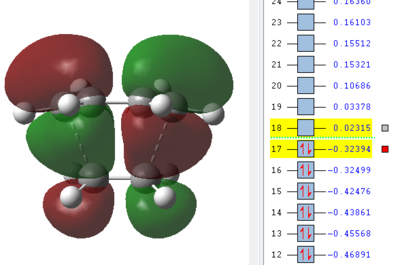Since it was suggested that the transition state has an envelope structure, also this was being examined to confirm it. The transition structure is the structure with the highest energy on the IRC path. The following bond lengths were obtained:

C1-C3 [Å]	C1-C5 [Å]	C3-C8 [Å]	C5-C11 [Å]	C8-C14 [Å]	C11-C14 [Å]
1.39749	1.38186	1.38184	2.11927	2.11932	1.38290

During this reaction the three π C-C double bonds between C1-C5, C3-C8 and C11-C14 are breaking and new σ C-C single bonds are formed between C5-C11 and C8-C14. The distance between the carbons between which a single bond is being formed is around 2.12 Å. The Van-der-Waal's radius for one carbon atom is 1.7 Å, which means that the distance between two carbons which are not interacting should at least be equal to 3.4 Å. The distance which is present is much smaller than that and therefore it can be said that during the transition state electronic interaction between these carbons is present already. However it is also known that an average C-C bond length for sp³ hybridised carbons is around 1.54 Å. The distance found in the transition state is larger than that, so the bond has not yet formed. The typical bond length for sp² hybridised C-C double bonds is 1.34 Å. The bond length found between carbons that used to be bound via a single bond is slightly larger than that which means that the bond is beginning to break. At the same time it is forming between C1-C3 where the bond length is also slightly larger, which is indicative for a concerted mechanism.

Diels-Alder reaction between Cyclohexadiene and Maleic Anhydride

This reaction is a classical example of the Diels-Alder reaction, with normal electron demand. This is because the dienophile (maleic anhydride) is electron poor due to the carbonyl groups attached, which are very electron withdrawing. This therefore lowers the energy of the LUMO. It can therefore be suggested that the major interaction happens between the LUMO of maleic anhydride and the HOMO of cyclohexadiene. One other detail of this reaction is that there are two possible geometries of the resulting product. This is because the maleic anhydride could potentially approach in two different fashions, assuming the cyclohexadiene is fixed in space. The resulting geometries are called endo and exo.

Exo Transition Structure

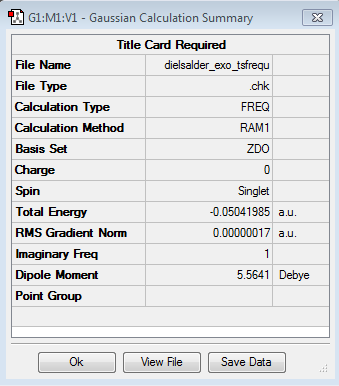
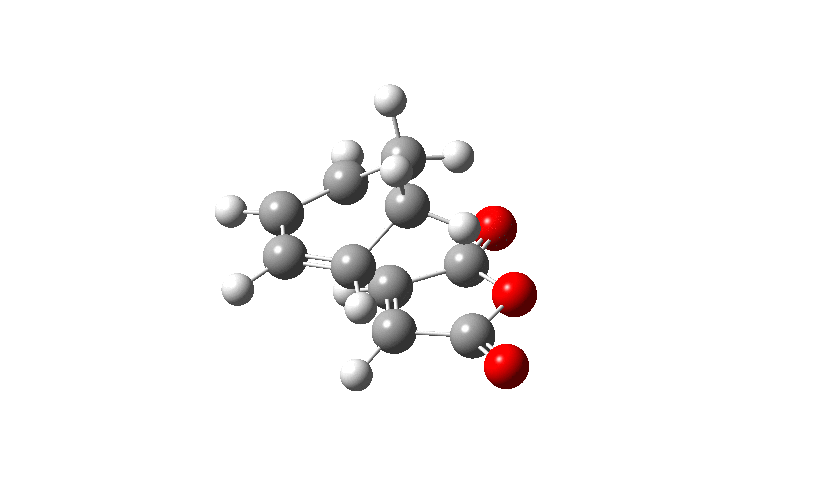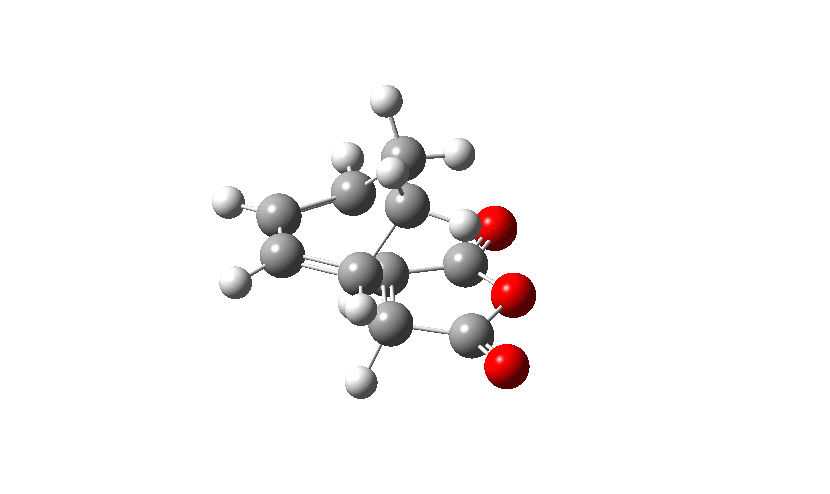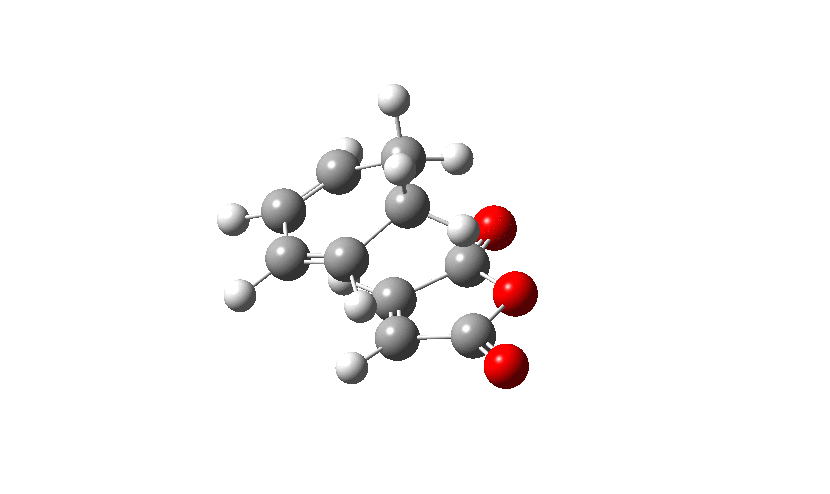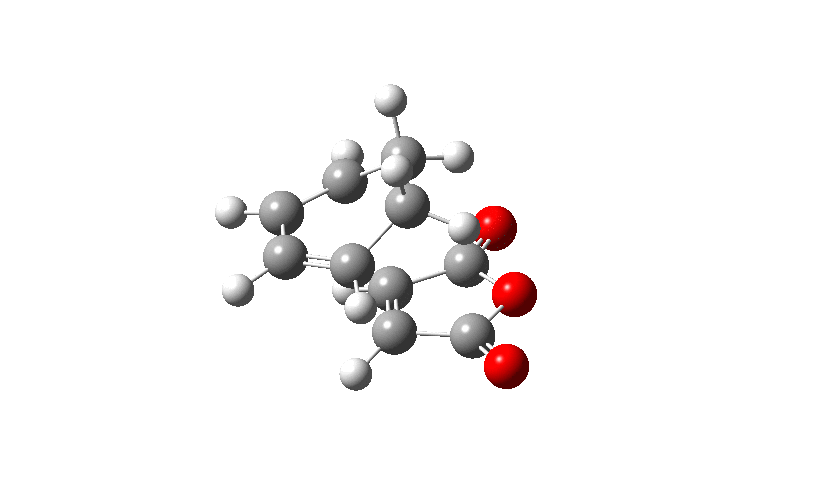
Firstly the Exo transition structure is being examined. To do so the transition structure was guessed and drawn on GaussView by drawing and optimising the seperate fragments (cyclohexadiene and maleic anhydride) seperately first and then pasting them into the same sheet. They were oriented into an exo-approach and placed approximately 2.0 Å apart. The AM1 semi-empirical method was used to optimise to a transition state (TS Berny). The log file can be found here The energy was calculated to be -0.05041985 a.u. and the imaginary frequency which is shown was calculated at -812.19 cm^-1. The presence of the imaginary frequency also confirms that a transition structure was found.

TS Summary Exo	Diels-Alder Exo Transition Structure	Imaginary Frequency

The best way to analyse the geometry of the transition structure is by looking at the bond lengths, as done and shown in the previous exercise.

C1-C4 [Å]	C3-C4 [Å]	C2-C3 [Å]	C2-C21 [Å]	C18-C21 [Å]	C9-C11 [Å]	C2-C9 [Å]	C13-C21 [Å]	Labelled Exo Transition State
1.39438	1.39676	1.39438	1.48976	1.52208	1.41011	2.17040	2.94508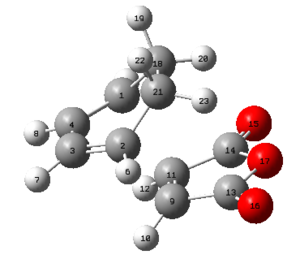

Also here it can be seen that the bonds that previously were double bonds (C1-C4, C2-C3, C9-C11) and the bond which is becoming a double bond (C3-C4) have very similar lengths, which is slightly larger than the average C-C double bond. It can be said that these are already in the process of breaking/forming in a concerted fashion. Furthermore there already is electronic interaction between C9-C2 and C1-C11 (where sigma single bonds are forming) since their separation is smaller than the sum of the two Van-der-Waals radii. It is also obvious that the distance between C13-C21 is much larger than the one for C2-C9 which means that the bridge, which results after the product is already in the process of forming and therefore the atoms bending up already. To investigate the electronic interactions in the transition state, the orbitals are pictured below:

HOMO -1	HOMO	LUMO	LUMO+1	LUMO+2
HOMO-1 symmetric	HOMO antisymmetric	LUMO antisymmetric	LUMO+1 symmetric	LUMO+2 antisymmetric

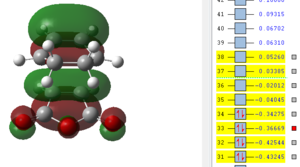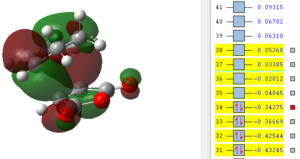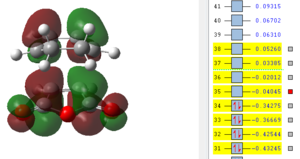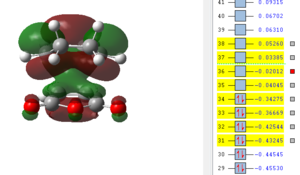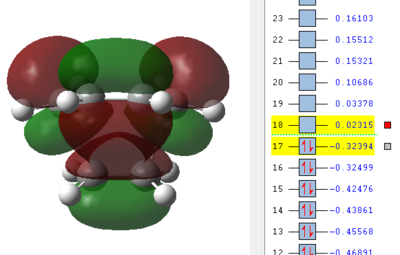
From the orbital pictures it can be seen that on all orbitals of the transition state only primary interactions exist and no stabilising secondary orbital interactions occur. The reason for this is that the C=O π* on maleic anhydride and the C=C π orbitals on cyclohexadiene are too far apart to interact due to the approach of the two molecules. Both HOMO and also LUMO are antisymmetric.

In order to see the reaction path of this approach without stabilising secondary orbital interactions an IRC path is run using the AM1 semi-empirical method. It can be nicely seen that the process occurs in a concerted mechanism. It can also be made clear how the reaction occurs with syn addition of the new bonds.

IRC for Exo-Product

Endo Transition Structure

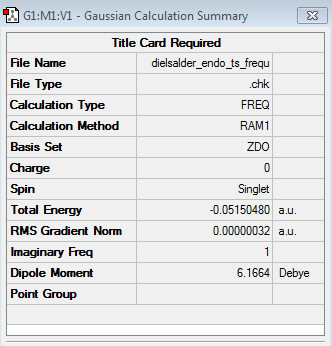
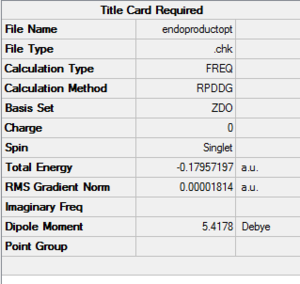
Also here the transition structure was guessed. In the endo approach the maleic anhydride molecule approaches the other way around, so that the carbonyl groups are below the double bonds of the cyclohexadiene. The optimisation for was run for the transition state using AM1/semi-empirical TS(Berny) method. log file here The energy of the transition state is -0.05150480 a.u. and the imaginary frequency was calculated to be at -806.39 cm^-1.

TS Summary Endo	Diels-Alder Endo Transition Structure	Imaginary Frequency

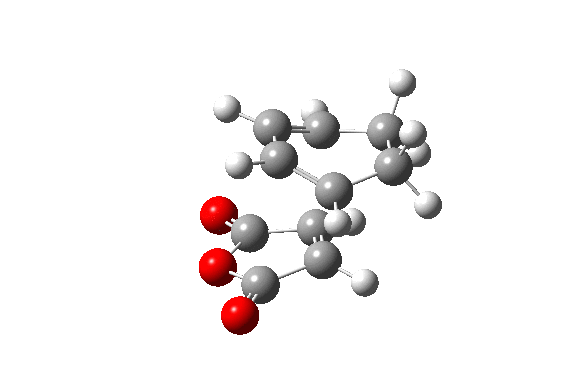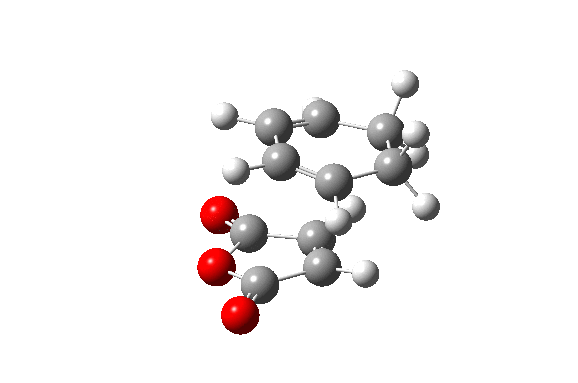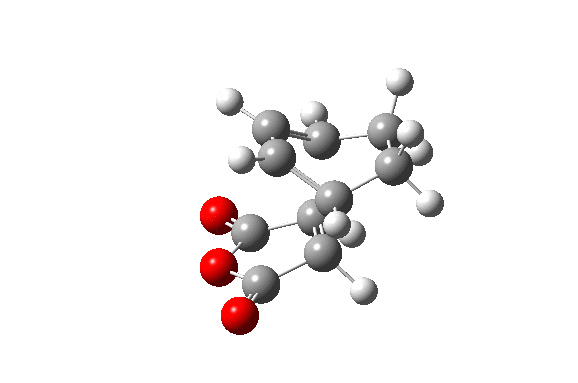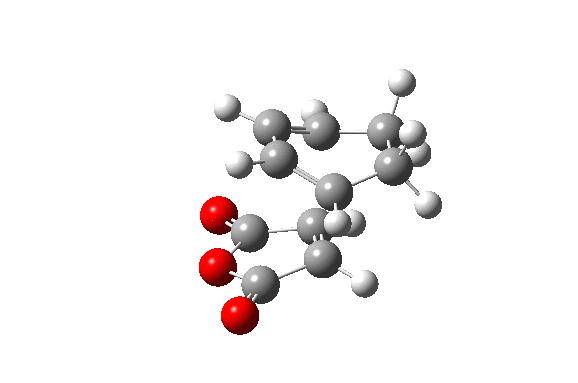
As also previously done for the exo-structure the geometry is also analysed for the endo transition state structure.

C1-C4 [Å]	C3-C4 [Å]	C2-C3 [Å]	C2-C21 [Å]	C18-C21 [Å]	C9-C11 [Å]	C2-C11 [Å]	C14-C21 [Å]	Labelled Endo TS
1.39305	1.39724	1.39305	1.49053	1.52297	1.40849	2.16239	3.89670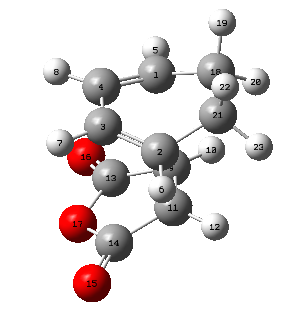

It can be seen from this overview that the bond distances in the transition structure are very much like the ones found in the exo transition structure. Also here the former C=C double bonds and the single bond becoming a C=C double bond have approximately the same bond length, which is between the average length for a C-C single bond and C=C double which indicates some delocalisation. Furthermore the distance between C2 and C11 is 2.16 Å which is again shorter than the sum of two Carbon van-der-Waals radii which suggests some form of electronic interaction already, however it is not a bond yet. The electronic interaction is also further investigated looking at the orbitals.

HOMO -1	HOMO	LUMO	LUMO+1	LUMO+2
HOMO-1 symmetric	HOMO antisymmetric	LUMO antisymmetric	LUMO+1 symmetric	LUMO+2 antisymmetric

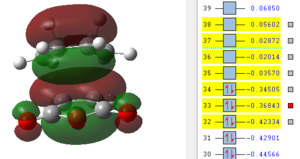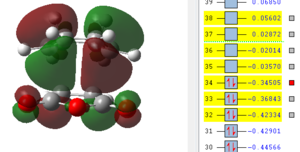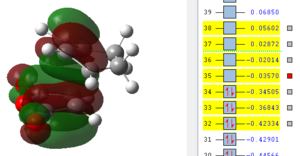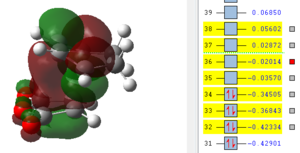In terms of the nodal properties for the HOMO it can be seen that the HOMO in both structures is not only antisymmetric but also shows many nodal planes. There several nodal planes but most of them can be found on atoms, which means it is not as energetically unfavourable as nodal planes between atoms (on bonds). What can be observed in these orbital representations is that in LUMO+1 and in LUMO+2 there are significant orbital overlap between the π orbitals of the C=C double bond and the π* of the C=0 bond of maleic anhydride. These are the so called "secondary orbital overlaps" which due to electron delocalisation over two molecules reduces the energy of the transition state structure. These secondary orbital overlaps are not possible in the exo form as it can be seen from the orbital pictures. Oxygen is a more electronegative atom than carbon, which means that it is lower in energy than the carbon, which therefore means that in the π bonding orbital it has a larger contribution to the orbital. The inverse is true for the antibonding orbital, in which the carbon has the larger contribution. This leads to a better overlap with the π orbital on the cyclohexadiene double bond. This leads to an energy advantage of 0.001 a.u.over the exo transition state, which is higher in energy. Therefore the endo product is the kinetic product, which is formed faster.

Also an IRC was run in order to see the product formation. log file here As for the exo product it can be seen that bond forming and bond breaking happen simultaneously, in a concerted fashion.

IRC for Endo-Product

Activation Energies

The activation energies for both geometries were calculated to see which one is kinetically favoured. For this all molecules were optimised using the Semi-empirical AM1 method again. The energies are shown in the table below and the difference in energy is converted into kcal/mol (1 hartree = 627.509 kcal/mol) Log files for the optimisation for 1,3-cyclohexadiene here and for maleic anhydride here

	Maleic Anhydride	1,3 cyclohexadiene	Sum Reagents	Exo TS	Endo TS	ΔEexo	ΔEendo
Energy [a.u.]	-0.12182394	0.02771130	-0.09411264	-0.05041985	-0.05150480	0.04369279	0.04260784

Converting the energy differences into kcal/mol the activation energy found for the exo TS = 27.418 kcal/mol and for the endo TS = 26.737. The difference between them is a significant 0.681 kcal/mol, which means that the endo transition state is easier to reach and therefore the endo product is the predicted favoured kinetic product. In order to investigate which one the thermodynamic product is both forms (exo and endo) of the product were optimised (Semi-empirical AM1) and the geometries and orbitals compared. The log files for the optimisation for the Exo product here and for the Endo product here

Summary Exo product	Exo product	Summary Endo product	Endo product
HOMO-1 symmetric	Exo Structure	LUMO antisymmetric	Endo Structure

It can be seen that the endo structure is also lower in energy than the exo structure. Therefore the endo structure is not only kinetically favoured by a lower energy transition state but is also the thermodynamically favoured product because the product has a lower energy. The reason for this can be explained looking at the geometry of the product.

Exo product	Endo product

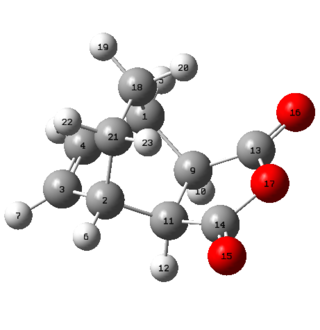
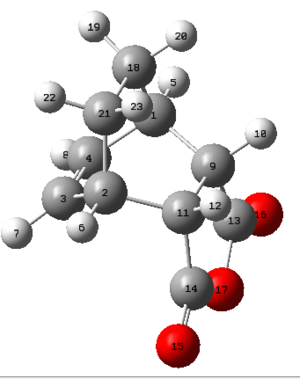
	C2-C21	C2-C11	H11-H23	O17-H23	C14-C21
Exo Product	1.53512	1.53620	3.75565	3.06579	2.94311
Endo Product	1.53807	1.53660	2.45651	5.08366	3.84939

The van-der-Waals radii for Carbon, Oxygen and Hydrogen are 1.70 Å, 1.55 Å and 1.20 Å respectively. It can be seen that in the endo product none of the distances between the atoms are any smaller than the sum of the van-der-Waals radii of the atoms involved. The distance between the two hydrogen atoms (on the bridge and on the maleic anhydride fragment) in the endo form are relatively close to the sum of the van-der-Waals radii but it still is not an unfavourable interaction in the sense they sterically clash with one another. In the exo form however, the distance between C14-C21 and C18-C13 is only 2.94 Å (highlighted in bold), which is far smaller than the sum of the van-der-Waal's radii which is 3.4 Å. It can therefore be said that this unfavourable interaction between the carbon atoms on the bridge and the carbonyl group carbons lead to strain in the exo-product which is not present in the endo-product. This could potentially be the reason for the exo product being higher in energy than the endo product.

Conclusion

Concluding it can be said that the Cope Rearrangement was studied successfully using computational methods. It was found that the Chair TS in the Cope Rearrangement of cis-butadiene is lower in energy than the Boat TS, though meaning that this transition structure pathway is kinetically favoured. Furthermore another pericyclic reaction - the Diels-Alder reaction - was studied for two different processes. In both the transition states were computed using AM1 Semi-empirical method. The transition state was always identified by the presence of an imaginary frequency. The Semi-empirical method was used, instead of more accurate ones like DFT or HF, because it was faster to calculate for big molecules involving oxygen atoms like maleic anhydride. It was found that for geometry calculations the different levels of theory in the methods do not differ significantly but for energy calculations it is worth spending more computational costs to obtain more accurate results. The selectivity for the Diels-Alder reaction was also studied and it was found that the endo structure is favoured both thermodynamically and kinetically. Kinetically it is favoured due to a lower activation energy and the favourable interaction between orbitals on carbonyl group and the double bond called 'Secondary orbital overlap'. The higher energy of the exo product was attributed to the strain between the carbons on the carbonyl group and the bridge, since the internuclear distance was smaller than the sum of the van-der-Waals radii.

Two major problems occur with computational methods. Firstly the transition state had to be guessed in order to optimise it. This worked here since the transition state structure was more or less known and could therefore be replicated. However, this would be a problem when new reactions need to be studied and the transition state is not known. Furthermore only one molecule is considered in the calculations. This neglects intermolecular interactions, because this one molecule is treated like an Ideal Gas. This could therefore lead to wrong values especially in energy calculations.

For further studies it could be interesting to investigate Diels-Alder calculations with more substituted reagents to investigate how much of an energy cost really occurs due to the steric strain in the exo product.

References

<references>