Rep:Mod:phys3mh4412
Abstract
In this experiment, two very well-known pericyclic reaction were studied. By using GaussView, computational analysis has been performed on model Cope rearrangement and Diels-Alder reactions. The Cope rearrangement was studied on 1,5-hexadiene. By first obtaining all 10 energetically distinct conformers, we have proceeded to calculating the energies and structures of the boat and chair transition states. It has been found that the lowest energy conformation is gauche 3, and that the chair TS is more favourable.
The Diels-Alder reaction was studied first on the ethene/butadiene pair. Energy minima for the TS were found; the HOMO and LUMO were visualised, upon which it was found that the symmetry of the orbitals plays an important role in the reaction. The reaction was further investigated on maleic anhydride/1,3-cyclohexadiene, where the effect of substituents was investigated. It was found that the secondary orbital overlap can be "seen" and that it gives predominately endo products, despite them being thermodinamically less stable.
Introduction
In this computational experiment, we have focused on two famous organic reactions, namely the Cope rearrangement and the Diels-Alder reaction. By using Gaussian, energies and structures of the starting materials and transition states were computed and visualized. In the case of the Cope rearrangement reaction, 1,5-hexadiene was used as the example molecule, whereas in the Diels-Alder part of the experiment, we focused on the reaction between cis-butadiene and ethene. The transition state structures and the effect of substituents on the regioselectivity were also investigated.
Both of the reactions studied are organic pericyclic reactions, which esentially means that in the transition state, electrons "flow" in a circle around the molecules involved. With regard to the arrow pushing, there is no beginning or end, and the electrons can go into either direction. This makes those reactions quite special, as usually, the beginning and the end of the "electron path" is clearly defined. The flow of electrons involves the electrons in the π clouds on the reactants. Both of the reactions studied here are very important in organic synthesis, as they provide a neat way of chaning the entire double-bond layout of a molecule in the case of the Cope rearrangement, whereas the Diels-Alder reaction is probably the most well-known ring forming reaction. It is therefore important that they are well understood and that factors, contributing to any selectivity are investigated. This was what we focused on in this experiment.
The aim of the first part of the exercise - the Cope rearrangement study - was to obtain the structures for the energy minima and the transition state structures and hence find the preferred reaction mechanism. In the second part (Diels-Alder), the structure of the TS was studied on a model reaction, and later, the effect of substituents on the regioselectivity was examined. HOMO and LUMO orbitals were plotted all the way through to help with the interpretation of what and why is going on.
The Cope rearrangement
The Cope rearrangement reaction involves a [3,3]-sigmatropic rearrangement and is a concerted pericyclic reaction (shown in Figure 1).

The exercise was done in 2 parts. The first involved optimising the reactants and products of the reactions, whereas the second part focused on optimising the chair and boat transition structures - the above figure is deceiving in a way that it presents the molecules as being 2-D, when in fact, they have specific 3-D structures. The structures were visualised using the program GaussView 5.0 and all the calculations were performed using Gaussian. For the structures of the different conformations refer to Table 1 at the bottom of the page. All energies given in Hartrees unless otherwise stated.
Part 1: Optimising the Reactants and Products
The most iconic reactant for the Cope rearrangement is 1,5-hexadiene (pictured in Figure 1). Roughly speaking, it can be present in 2 general conformations, depending on how the central C-C bond is rotated - the antiperiplanar or gauche conformation. The experiment was started by investigating the energy and conformation of 1,5-hexadiene drawn in approximate app conformation. The structure was cleaned up and the energy minimum was calculated using the Hartree Fock level of theory at the basis set 3-21G. The results were as follows:
E(RHF) = -231.69253528, point group: Ci – later identified as Anti 2
Afterwards, a molecule of 1,5-hexadiene was drawn in in approximate gauche conformation. Again, it was cleaned up and the HF/3-21G calculation was performed. The expected minimum energy of this conformation was expected to be higher than the energy of the anti conformation used before. The results were as follows:
E(RHF) = -231.69266122, point group: C1 – later identified as Gauche 3
Hence, for the 2 specific structures above, the energy was in fact lower for gauche than for the anti conformation. Gauche 3 later proved to be the lowest energy conformation of them all, with anti 2 being the 3rd lowest (with anti 1 being the second lowest in energy), which means that the first two "guess" molecules yielded quite good results in terms of the energy minima calculations. This information was obtained after drawing all 10 distinct conformers of 1,5-hexadiene. In theory, there are 27 possible staggered low-energy conformations, but only 10 are of different energy, which is a consequence of their symmetry and the fact that some of those conformers are enantiomers of each other [1, 2]. The table below contains all the structures and energy data about the 10 distinct conformers that were investigated. During the calculations, comparisons to the known structures and their energies (supplied) were made to check whether the conformations match in terms of the energy and point groups assigned to them.
Table 1: anti and gauche conformers of 1,5-hexadiene
| Conformer | Structure | Point group | Energy/Hartrees (HF/3-21G) |
Relative Energy (kcal/mol) |
||
|---|---|---|---|---|---|---|
| Anti 1 (B) | C2 | -231.69260 | 0.04 | |||
| Anti 2 (E) | Ci | -231.69254 | 0.08 | |||
| Anti 3 (K) | C2h | -231.68907 | 2.25 | |||
| Anti 4 (H) | C1 | -231.69097 | 1.06 | |||
| Gauche 1 (J/L) | C2 | -231.68772 | 3.10 | |||
| Gauche 2 (A) | C2 | -231.69167 | 0.62 | |||
| Gauche 3 (D/F) | C1 | -231.69266 | 0.00 | |||
| Gauche 4 (C) | C2 | -231.69153 | 0.71 | |||
| Gauche 5 (I) | C1 | -231.68962 | 1.91 | |||
| Gauche 6 (G) | C1 | -231.68916 | 2.20 |
It can be seen that the energies of the conformers vary slightly. The differences are small, but this is to be expected - they are only the result of rotations along the three C-C bonds present in the molecule. The differences in energies arise from different sterical interactions and resonance stabilising effects, which are pronounced to a different degree in each of the conformers. Below, Newman projections for all of the above structures are shown - the explanation will be done using those as reference.
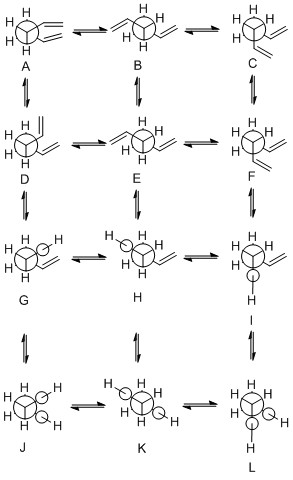
Conformers D, F and J, L are enantiomers, hence there are only 10 distinct energy conformations out of the 10 displayed above. The Newman projections were drawn by first rotating about the central C-C bond for conformations A-C while keeping the double bond fragments antiparallel. The second row (D-F) is obtained by again rotating about the central C-C, but this time keeping the double bond fragments parallel. Conformations G-I can be made by making one of the sp3-sp2 C-C bonds into a s-cis conformation while again rotating about the central C-C. The final row (J-L) can be drawn by making both sp3-sp2 C-C bonds s-cis. Matching to the Anti 1-4 and Gauche 1-6 has been made in table 1 above, based on inspection of dihedral angles [2].
The lowest energy conformation is, as briefly mentioned above, gauche 3 (D/F). This is because of possible stabilisation effects between the π orbital and the vinyl proton of the other double bond. Also, there are no destabilising steric effects present in the molecule which would disfavour the gauche conformation (How do you evaluate absence of disfavouring steric effects? Perhaps a better way to put it is to say that whatever steric effects there are, they are compensated by other stabilizing effects? João (talk) 00:25, 26 December 2014 (UTC)). Following the gauche 3 are the anti 1 and 2 (B, E respectively), the energy of which is only slightly higher. As it can be seen from the structure figures of those 2 molecules, they are the most optimised structures in terms of eliminating the steric ineractions - in fact, they are sterically less hindered than gauche 3 (D/F), but they lack some of the π stabilisation, which brings their energy only slightly above gauche 3. Following the lowest 3 energy conformations are gauche 2 and 4 (A, C respectively), the energy of which is brought up by the fact that the vinyl groups are brought closer together (2.7A and 3.4A between vinyl protons and C2/C5 respectively, compared to >4A for anti 1, 2), while eliminating the π interactions present in gauche 3 as the angles between protons and the π cloud are less favourable - vinyl proton lies just above the π cloud in gauche 3, whereas it is moved out of it in A and C. The interatomic distances are also increased (C2-C5: 3.06A, 3.08A in A, C, 3.09A in gauche 3; vinyl H-C2/C5: 3.4A, 2.9A in A, C, 2.8A in gauche 3)[2].
After those lowest-energy 5 conformers, the energy is raised quite significantly to reach anti 4 (H). That is because any π cloud-H interactions are now 0, and also the steric strain is larger as one of the vinyl groups wraps under the central C-C. Steric strain is further increased in gauche 5 (I) where the distance between terminal protons and the vinyl proton starts to play a role - it amounts to only 2.6A. In gauche 6 (G) the distance between the vinyl groups decreases, as they are both wrapped into the same direction, reducing their distances to 2.9A. Anti 3 (H) and gauche 1 (J/L) are the highest in energy because of the C1-C4 proton interactions in anti 3 (distance only 2.4A), whereas in gauche 1 it is only 2.3A.
In summary - reducing the interatomic distances and making the π cloud-vinyl H orbital interactions impossible causes the conformers to gradually increase in energy. The effects can be infered by simple inspection of conformer structures in table 1, where the disappearance of possible favourable interactions and the group spacing decrease can be seen fairly clearly (Newman projections are slightly less intuitive as one is not able to clearly see the groups in 3-D)[2].
Despite the data listed above that supports the energy ordering of conformers, it must be stated that not all references agree with it - different experiments show either anti 1 ([1]) or gauche 3 ([2]) to be the lowest energy conformer. This is probably due to the really small (practically negligible) energy difference between the two. 1,5-hexadiene is possibly the molecule that is on the midpoint between conjugated alkenes and straight chain alkanes, hence anti and gauche are in a way both the preferred conformation.
After the extensive analysis of the 10 conformers using the HF/3-21G method, the anti 2 structure was chosen to be reoptimised using a different, more advanced level of theory, namely the DFT theory with the B3LYP functional and 6-31G* basis set. The results obtained using this were:
E(RB3LYP) = -234.61171061, point group: Ci
By subtracting the energies obtained by HF/3-21G and RB3LYP it can be seen that the difference between the two is 2.919175, meaning that the DFT calculation gives a lower value of energy for a certain molecular structure. However, the geometries remain the same - both calculations yield a Ci point group. (Had the central bond length increased by 9Å, the symmetry point group would still be Ci but would you say the geometries are the same? João (talk) 00:25, 26 December 2014 (UTC))
As well as providing more accurate energy values, DFT theory also enables frequency calculations to be carried out (You can also do frequency calculations with Hartree-Fock and most other methods João (talk) 00:25, 26 December 2014 (UTC)). Those are quite valuable, as the calculation of the energy minimum only gives the energy of the molecule on a bare energy surface, which is not useful when compared to experimental values. This means that additional terms need to be included in the calculation. The frequency calculation takes those into account, as well as enables the visualisation of the vibrations and predicts an IR spectrum of the compound. The latter 2 "visual outputs" are shown in Figure 3 below.
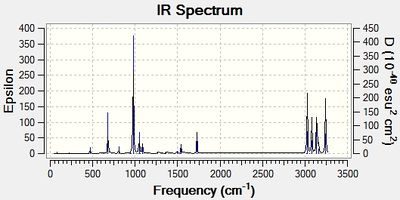
The vibration shown is the vibration of the ground state of anti 2 (By ground state do you mean lowest frequency? There will be a zero point energy associated with all vibrational modes, all modes can be on the ground vibrational state simultaneously João (talk) 00:25, 26 December 2014 (UTC)). The fact that there are only real, positive values for frequencies present in the output file confirms that the structure is indeed a minimum. The spectrum prediction is as expected - it shows all the important vibrations. Peaks in the 2900-3250 cm-1 region are due to Csp3-H and Csp2-H vibrations (vibrations above 3000 cm-1 indicate non-saturation, as is the case here), whereas the peak at approximately 1700 cm-1, indicates a C=C double bond. Below 1500 cm-1, a fingerprint region is observed.
The additional energy data can be seen by accessing the data file that Gaussian provides. There are 4 types of values there; they can be located under the "Thermochemistry" section. They represent the following:
i) the sum of electronic and zero-point energies (potential energy at 0K = zero point energy; E = Ee+ZPE)
ii) the sum of electronic and thermal energies (energy at 298.15K/1bar, including translational, vibrational, rotational energies; E = Ee+Etrans+Evib+Erot)
iii) the sum of electronic and thermal enthalpies (contains a RT correction; H = E + RT)
iv) the sum of electronic and thermal free energies (includes the enthropic contribution; G = H - TS)
The advanced thoeory calculations were done for anti 2 at 298.15K and also 0K to be able to compare the energies of the minima at different conditions. The results of the calculations are shown in Table 2 below:
Table 2: Results of DFT/B3LYP/6-31G* calculations on DFT optimised anti 2, at 0K and 298.15K
| Energy type | At 0K (E in Hartrees) | At 298.15K (E in Hartrees) |
|---|---|---|
| E = Ee+ZPE | -234.416259 | -234.416259 |
| E = Ee+Etrans+Evib+Erot | -234.416259 | -234.408966 |
| Sum of Ee and thermal enthalpies | -234.416259 | -234.408021 |
| Sum of Ee and thermal free energies | -234.416259 | -234.447881 |
By comparing the energies it can be seen that the sum of electronic and zero point energies is the same, regardless of the temperature at which the calculation was done. This makes sense, as this sum represents the energy on a bare energy surface - it is the value also given by the Hartree-Fock theory (although it is less exact in that case). The sum of electronic, translational, vibrational, and rotational energies has a lower value when the calculation is performed at 0K than when it is done at 298.15K - which also matches expectations, as there is less energy in the system at 0K. Careful inspection actually shows that Ee+ZPE = Ee+Etrans+Evib+Erot at 0K, which means that Etrans+Evib+Erot = 0 at 0K. This is also as expected, as the molecules are only expected to posses electronic energy and residual energy (ZPE) at 0K, when all translational, rotational, and vibrational ("macro") motion stops. The sum of Ee and thermal enthalpies is also lower at 0K than at 298.15K, which is the consequence of the system having a heat capacity of 0 at 0K (as the system cannot change electronic states - it is locked in the ground state because of insufficient thermal energy), which gives rise to a lower enthalpy, according to the relation Cp=ΔH/ΔT. The last value however, the sum of Ee and thermal free energies is higher at 0K than it is at 298.15K (This should not be the case. I suspect a typo writing down the table João (talk) 00:25, 26 December 2014 (UTC)). This is because the thermal free energy is equal to the amount of work that a system can perform and is given by the difference between the internal energy and the enthropy (Entropy and internal energy don't have the same units João (talk) 00:25, 26 December 2014 (UTC)). As the enthropy is larger when the system is at a higher temperature (as stated before), this final value is lower for the system at 298.15K than for 0K.
Part 2: Optimising the Chair and Boat Transition structures
In this section, optimisation of both conformers of the transition state of the Cope rearrangement was done using 3 different methods - the Hessian method, frozen coordinates method, and the QTS2 method. The two conformers of the transition state are the chair and boat structures, with the boat being slightly higher in energy. They are depicted in the figure below:
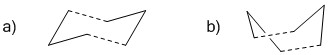
Firstly, we focused on optimising the chair transition state. The Hartree-Fock theory with 3-21G basis was used to do the calculations. In this excercise, a guess chair transition was first drawn by putting 2 C3H5 allyl fragments in a chair conformation and setting the distance between the two terminal carbons to approximately 2.2A (2.15A, 2.17A). A transition state optimisation method was then run (TS Berny) and the output structure was analysed. The results were:
E(RHF) = -231.61932216, point group: C2h, C-C distances: 2.02A, 2.02A
The value of one of the vibration frequencies was negative (-818 cm-1, which confirms that a transition state was identified - the negative frequency indicates that the identified point is a maximum on a potential surface (A maximum along a particular this direction, a minimum with respect to all others João (talk) 00:25, 26 December 2014 (UTC)), which a transition state indeed is. The structure and vibrations can be seen below:
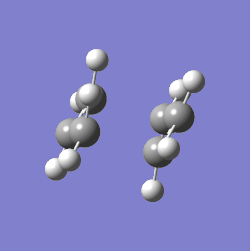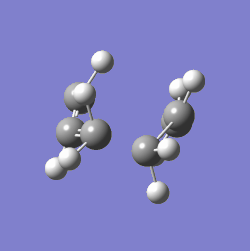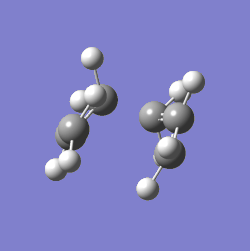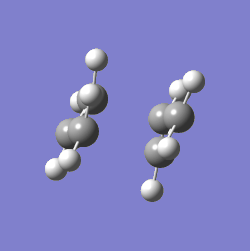
The transition state looks as expected - as it vibrates, the ends of the allyl fragments approach each other, showing how the molecule reacts. This means that a good transition structure has been identified straight away.
Seconly, a different approach was used to get to the same result as above. Again, the guess structure was used, but this time it was optimised using the frozen coordinate method. The end carbons on the allyl fragments were frozen and then the structure was optimised again, this time yielding the following:
E(RHF) = -231.61932236, point group: C2h, C-C distances: 2.02A, 2.02A
Again, there was the -818 cm-1 imaginary vibration. By comparing the results, one can conclude that they are virtually identical - a disagreement occurs only in the 7th decimal place of the energy value, which is a negligible difference. This means that the same TS structure was successfully identified using both approaches. This concluded the search for the chair TS, as the structure is fairly easily determined. The reproducibility of the result using 2 different approaches also speaks positively about the correctness of the result.
After identifying the structure of the chair TS, the boat TS was to be determined. This was done using a yet another method, namely the QTS2. This method differs from the previous two - instead of inputting a guess transition state structure and minimising its energy, the reactant and product molecule are supplied to the programe. Gaussian then interpolates between the two structures and tries to identify the transition state between them. The reactant chosen was the anti 2 structure from before. The starting material and product in this case only differed by the way the carbons are ordered, and that information was supplied to the program in terms of careful labelling of all of the atoms involved, such that it was clear which "atom goes where" as the reaction takes place.
As stated, the calculation was attempted with anti 2. At first, no changes were applied to the molecule, and the reaction was run using the input structure below:

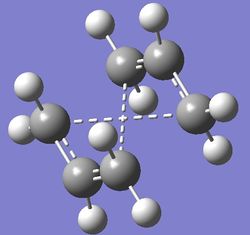
Figure 6: Initial input and the output files for boat TS calculation using QTS2
As it can be seen, the TS identified looks more like a chair oand the program also suggested a very peculiar reaction pathway (The program is not suggesting anything. In quantum mechanical calculations the connectivity of the atoms in the molecule are not defined, all that counts is the inter-atomic distance. The dashed lines are meaningless, and in this case they are tracking what atoms were "connected" in the input structures João (talk) 00:25, 26 December 2014 (UTC))- such that the ends of the allylic fragments would need to cross or one of the fragments would need to invert in order to react. This is obviously wrong and is also confirmed by the fact that the vibration frequences were not calculated and hence this TS does not exsist in this form (There should be no reason why a frequency calculation cannot be done in this structure. In fact it should be an "ordinary" chair transition state João (talk) 00:25, 26 December 2014 (UTC)). Obviously, a correction needs to be made. As the program is designed so that the allyl fragmets were only translated in this case (when a rotation was needed), it is clear that the correction that needs to be employed will focus on correcting the reactant and product structures so as to resemble the transition state more closely and hence "help" the program to identify the correct TS structure. This was done so that the central C2-C3-C4-C5 dihedral angle was set to 0°instead of +/-180°and also the bond angles between C2-C3-C4 and C3-C4-C5 were changed to 100° (from 111.36°). This yielded the following conformation:
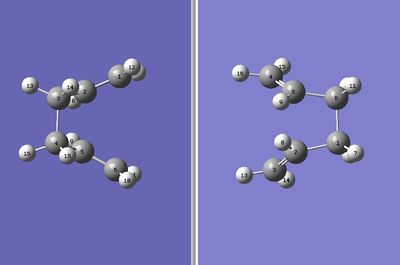
Figure 7: Improved input and the output files for boat TS calculation using QTS2
It can immediatelly be seen that setting a better starting and end points for the reaction yields much better results. The boat TS has been identified - confirmed by the geometry of the product and also by the fact that there are now vibrations present - indicating how the reaction proceeds. There is also 1 imaginary vibration at -839 cm-1, confirming that this is indeed a structure of a TS. Other results are as follows:
E(RHF) = -231.60280219, point group C2v, C-C distances: 2.14A, 2.14A
A QTS3 calculation was also done. In addition of providing the reactant and product structures to the program in QTS2, the guess transition structure is also included here (refer to Figure 8 below). The result of the calculation was almost identical to the QTS2 result and is as follows:
E(RHF) = -231.60280206, point group C2v, C-C distances: 2.14A, 2.14A
The imaginary vibration frequence here was also -839 cm-1. The two transition states are hence the same - the only difference is a variation in the 7th decimal place in the value of the energy. The input and output files are shown below. It is clear that the TS structure obtained by this method matches the one obtained by QTS2.
Figure 8: Improved input and the output files for boat TS calculation using QTS3
Despite successfully obtaining the structures of both of the transition states, it is hard to say which conformer of 1,5-hexadiene they lead to just by looking at their structures. To determine this, another calculation needs to be done - one that traces the path of the transition state as the product forms and then identifies a minimum. The properties of this minimum (conformation, energy) can then be compared to the conformers of 1,5-hexadiene drawn above in Table 1. The method is called IRC (intrinsic reaction coordinate). It was used on the optimised chair transition structure. The calculation was run in the forward direction, set to 50 points. The result was the following:
E(RHF) = -231.69161105, point group C2 - identified as gauche 2
This is quite an interesting result. It shows that the calculation went to one of the product structures, but it is not the global minimum structure. The IRC plots also show this:
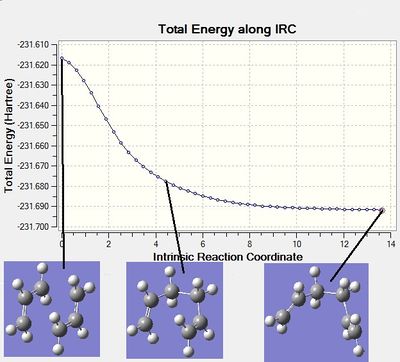
Figure 9: IRC calculation plot
As it can be seen from the graphs above, the plots did not yet reach a minimum - the plot is still slanting down instead of fixing on a minimum value. Also, the identified structure (gauche 2) is not the minimal-energy conformer - based on the data from part 1, the minimal energy conformer is gauche 3. In order to improve this result, one of 3 things can be done:
i) running the IRC again with more steps (which is time consuming and gives no guarantee that the correct minimum will be reached)
ii) calculating a minimum on the obtained structure (if it is far away from the global minimum, it will not be obtained)
iii) by doing the IRC again, this time specifying to calculate force constants at every step
The result here was first attempted to be improved by using the method i), which still produced the gauche 2 structure. Next, ii) was attempted, but even after 150 steps (instead of the initial 50), the structure proposed by the program was gauche 2. The third method was basically employed in the initial calculation, as it was already specified to the program to always calculate the force constants. It seems that it is indeed hard to identify the minimum/energy conformer. It is possible that the program fails to do so because the conformers lie really close together in energy and hence makes an incorrect judgement that the minimum has been reached.
(I suspect that your first IRC calculation has converged. There is no reason why the IRC should yield the global minimum on the PES. If an algorithm finds a local minimum, with no other information, how can it tell it is not the global minimum? João (talk) 00:25, 26 December 2014 (UTC))
Finally, after establishing the boat and chair TS as well as determining the reaction pathway, it is possible to calculate the activation energies needed to drive the reaction via either of the transition states. This is done by simply calculating the difference in energy betweent he reactant (anti 2) and the respective TS. However, the values of energies must be calculated using the DFT method using the B3LYP/6-31G* level of theory to get more exact energy values. HF/3-21G optimised structures were taken as the starting points. All of the results are summarised in the table below.
(Did you recalculate the energy at the previously found TS geometries, or did you do a re-optimization of the transition state? If you re-optmized, how much did the geometry change? Was a single-imaginary frequency preserved? João (talk) 00:25, 26 December 2014 (UTC))
Table 3: results of HF/3-21G and B3LYP/6-31G* optimisations of anti 2, chair TS, and boat TS (E in Hartrees)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | E = Ee+ZPE | Sum of Ee and thermal energies | Electronic energy | E = Ee+ZPE | Sum of Ee and thermal energies | |
| at 0K | at 298.15K | at 0K | at 298.15K | |||
| Anti 2 | -231.69253518 | -231.539539 | -231.532565 | -234.61171061 | -234.469219 | -234.461871 |
| Chair TS | -231.61932236 | -231.466703 | -231.461344 | -234.55693090 | -234.414908 | -234.408980 |
| Boat TS | -231.60280219 | -231.450934 | -231.445305 | -234.54307881 | -234.402354 | -234.396011 |
The values in the above table agree to a great extent with the values provided. HF/3-21G values agree to the last decimal place, whereas all of the B3LYP/6-31G* values agree to 4 decimal places. Using the numbers above, activation energy calculations were then performed; they are summarised in Table 4. All the energies were converted from Hartrees to kcal/mol (1 Hartree = 627.509 kcal/mol) for simpler comparison to the provided experimental values.
Table 4: Activation energies
| HF/3-21G | B3LYP/6-31G* | Experimental value | |||
|---|---|---|---|---|---|
| ' | at 0K | at 298.15K | at 0K | at 298.15K | at 0K |
| Ea, chair TS | 45.70 | 44.69 | 34.08 | 33.19 | 33.5 ± 0.5 |
| Ea, boat TS | 55.60 | 54.76 | 41.96 | 41.33 | 44.7 ± 2.0 |
It is quite clear that the values, obtained by computational methods here, agree really well with the experimental values, which speaks very positively about the methods used. As it can be seen, the activation energies are higher for the boat transition state in all cases, which agrees with the previously established fact that the chair conformation is more energetically favourable (=lower in energy). It is very satisfying to see such results - it defenitely confirms that computational methods are very useful and even more importantly - reliable.
This concludes the first exercise of the computational experiment. We have successfully obtained 10 energetically distinct minimum energy conformations of 1,5-hexadiene and also determined the structure of the two energetically different transition states, as well as calculated the activation energy needed to cross the transition state in each of the conformers.
The Diels-Alder reaction
The second exercise of the experiment dealt with the Diels-Alder reaction. It is a very well known concerted pericyclic reaction, more specifically a [4πS+2πS] cycloaddition. It involves a diene and a dienophile coming together to form a ring via a cyclic transition state, as depicted in the figure below.
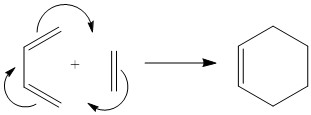
Figure 10: Diels-Alder reaction scheme
For the Diels-Alder reaction to proceed, the reactants' orbitals must be able to overlap - the LUMO of one must overlap with the HOMO of the other and vice versa, which leads to the formation of 2 new HOMO and LUMO orbitals in the product. The imporant factor that determines the ability of orbitals to overlap is their symmetry. This means that if the symmetries of the corresponding HOMO/LUMO pairs are the same (symmetric/antisymmetric - a/s) the two reactant molecules can come together and form the product.
In this exercise, the semi-empirical AM1 model was used for calculations.
The computation was begun by building and optimizing the geometry of cis-butadiene. Molecular orbitals (the HOMO and LUMO) were then visaualised using GaussView. The results were as follows.
E(RAM1) = 0.04879724, point group C2v
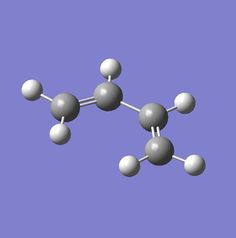
The molecule itself and its HOMO and LUMO orbitals are shown in the figure below.
 b)
b) 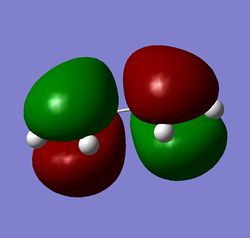 c)
c) 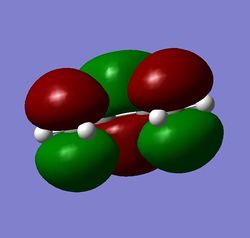
Figure 11: a) cis-butadiene, b) its HOMO, c) its LUMO
The HOMO and LUMO figures are quite straightforward - it can be seen at a first glance that HOMO is antisymmetric with respect to the plane perpendicular to the alkene groups, whereas the LUMO is symmetric.
The next step now is to construct the transition state of the reaction between ethylene and butadiene. By guessing the structure of the transition state (the distances between the terminal C atoms on each fragments were set to 2.2A) and then optimizing to a TS (Berny), a transition state is obtained. The results were the following:
E(RAM1) = 0.11165468, point group Cs, C-C distances: 2.12A, 2.12A
C-C distances here are as expected - slightly shorter than 2.2A (guess), similar to what happened in the Cope rearrangement part of the assignment. The distance btween the terminal C on each fragment hence lies somewhere in between an average Csp3-Csp3 single bond (~1.5A) and the sum of the Van der Waals radii of the C atoms (1.7A+1.7A = 3.4A) - in the region where there definitely is some interactions between the atoms, but they are not yet covalently bonded. Furthermore, the C=C double bond in ethene elongates from 1.35A (normal Csp2-Csp2) to 1.38A in the transition state. The bonds in butadiene change from 1.34A and 1.45A to 1.38A and 1.40A (terminal C=C, central C-C respectively)- an indication that the terminal C=C double bonds are changing into C-C single bonds, whereas the central C-C is becoming more C=C-like. The change of structures is also shown in the angles - the H-C-C-H dihedral angle in ethene changes from 180° to 154.5° as hydrogens bend away from the butadiene chain to accomodate the newly forming C-C bonds between the two fragments. The H-C-C-H dihedral angle on the terminal vinyls similarly changes from 180° to 155.6° on butadiene.
In addition to all this, as this is a transition state, an imaginary frequency is expected among the vibrations. It was shown to have a value of -956 cm-1. The structure and the imaginary vibration of the TS, as well as the HOMO and LUMO of the transition state are shown below.
 b)
b)  c)
c) 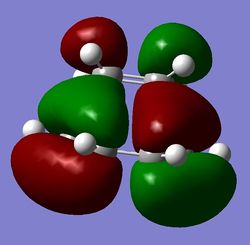 d)
d) 
Figure 12: Ethene + cis-butadiene TS: a) -956 cm-1, b) 147 cm-1, c) HOMO of TS, d) LUMO of TS
In a), the favourable vibrations which show that the bonds are formed simultaneously on both ends of the fragments can be seen. The vibrations depicted above are those of the imaginary frequency. The lowest positive frequency however (shown in b), shows the molecule vibrating in a way that implies that the bonds are formed sequentially as the ethene fragment is rotates first clockwise and then anticlockwise, whereby it gets approaches the ends of the butadiene first with one and then the other carbon. However, this vibration no longer shows the transition state, as it is not the one that occurs at the peak of the potential curve. This means that the vibration in a) is the one that shows the correct bond forming, which hence happens simultenously.
From parts b) and c) of Figure 12, it can be seen that the HOMO in the TS is antisymmetric and is composed of the butadiene HOMO and ethene LUMO (both antisymmetric), whereas the LUMO is composed of the butadiene LUMO and ethene HOMO and is hence symmetric. The orbital overlap is hence favourable in both as symmetries match, which means that the reaction is allowed. As the electrons are favourably distributed when the molecules are in their ground states, this reaction proceeds just by thermal activation. The fact that the HOMO of the butadiene indicates that the diene is the electron rich fragment which donates its π density into the π* orbital of ethene (dienophile LUMO). This process is termed "normal demand". The process can happen the other way around ("inverse demand") by placing electron withdrawing groups on the diene and/or electron donating groups on the dienophile, whereby the dienophile HOMO would donate into the LUMO of the diene, because of the now-changed energies of the orbitals in the molecules.
Finally, at the end, the effect of substituents on the Diels-Alder reaction was investigated. The model molecules used for this part were maleic anhydride (dienophile) and cyclohexa-1,3-diene (diene). When they react, 2 products are observed: the endo and exo product, shown in the figure below.
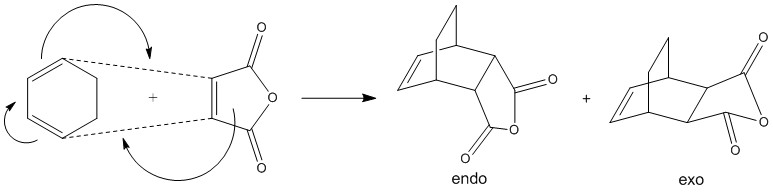
Figure 13: the endo and exo products
In this reaction, the endo product is formed predominately. The selectivity arises from two orientations that the maleic anhydride can assume in the transition state. When reaction to give the endo product, it is aligned so that the substituent is pointing towards the π system, whereas in exo, it is pointing away from it. The fact that endo is formed in excess implies that the energy of the transition state for endo is lower than that of exo - endo is kinetically favoured. This observation was tested by creating both of the transition states using GaussView and then comparing the TS energies and structures. Both structures were optimised using the frozen coordinate method introduced during the Cope rearrangement exercise. The results obtained were as written below. The first value of the distances (C-C distances) represents the distance between the reacting C atoms, the second is the distance between the maleic C atoms and the "opposite" C=C or C-C (endo, exo respectively) group (distances indicated in Figure 14). In both of the structures, imaginary vibration frequences have been identified (-806 cm-1 for endo, -812 cm-1 for exo), therefore confirming that transition states have been found.
a) endo: E(RAM1) = -0.05150469, C-C distances 2.16A, 2.16A; through space distances (maleic C - opposite C=C): 2.89A, 2.89A
b) exo: E(RAM1) = -0.05041967, C-C distances: 2.17A, 2.17A; through space distances (maleic C - opposite C-C): 2.94A, 2.95A
 ii)
ii) 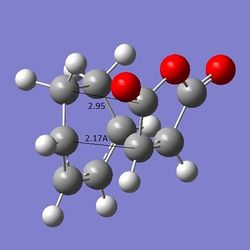 Figure 14: The endo and exo products (a) i) and ii) respectively) with interatomic distances labelled, endo and exo TS vibrations (b) i) and ii) respectively).
Figure 14: The endo and exo products (a) i) and ii) respectively) with interatomic distances labelled, endo and exo TS vibrations (b) i) and ii) respectively).
By calculating the difference in energy between the two TS and converting the value to kcal/mol, it can be determined that the conformations differ by about 0.68 kcal/mol, favouring the endo TS. It can be seen from the figure that the difference between the two isomers arises from the orientation of maleic anhydride in the TS ("up" or "down" relative to the diene). Judging just by the interatomic distances of the C atoms that are forming bonds, it seems that the endo TS is more favoured because the distance is slightly shorter than in the exo TS (Why does a shorter distance imply lower energy transition state? João (talk) 00:25, 26 December 2014 (UTC)). However, the maleic C - opposite C=C/C-C group distances are smaller for endo than for exo (For the exo structure, should you know compare the distance to the H atoms which are closer? João (talk) 00:25, 26 December 2014 (UTC)), making the endo TS more sterically crowded. The endo TS therefore gives a thermodinamically less stable product (Can you make thermodynamic inferences from the properties of the transition state? João (talk) 00:25, 26 December 2014 (UTC)). Hence, there must be a stabilising effect greater in magnitude than the destabilising effect of the steric hindrance present in the endo TS. It turns out that that is indeed the case - there are favourable orbital overlaps possible in the case of the endo TS which are absent in the exo TS. This is termed the secondary orbital overlap (SOO). It involves the π and π* orbitals of the diene and dienophile stabilising each other. Using the AM1 theory, it can be seen in the LUMO+1 orbital, as shown below. This is odd however - the LUMO+1 is not really involved in the reaction. The SOO overlaps were expected to be seen in the HOMO/LUMO pairs of the orbitals, but were not noticed there (Did you check such effect in orbitals lower in energy than the HOMO? João (talk) 00:25, 26 December 2014 (UTC)). The possible positive interactions with some oxygen orbitals that are in phase with the orbitals forming new bonds are indicated, but they do not actually show overlaps. Also, the oxygen atoms are not the ones expected to take part in the SOO stabilisation. This is shown in the figures below.
 b)
b) 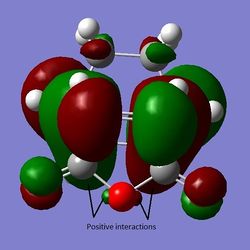 c)
c) 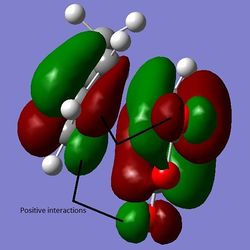
Figure 15: The endo LUMO+1, HOMO, and LUMO (a), b), c) respectively).
The overlap in in a) in red shows the SOO in LUMO+1. Now, if the endo LUMO+1 is compared to the one seen in exo, it is fairly obvious that the extent of the stabilising interactions (secondary orbital overlaps) is smaller, as the overlap density is smaller if exo LUMO+1 is plotted (shown in green in Figure 16). Also, the possible oxygen interactions with the rest of the forming molecule are now absent, as the "oxygenated part" of the molecule is now pointing away from the ring-forming system.
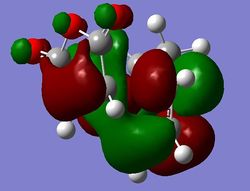 b)
b) 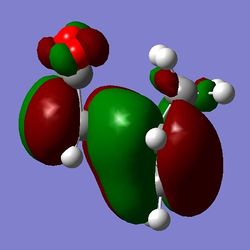 c)
c) 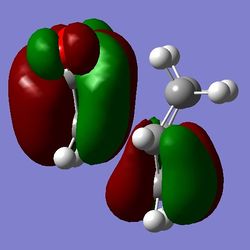
Figure 16: The exo LUMO+1, HOMO, and LUMO (a), b), c) respectively).
The smaller extent of SOO in exo is also confirmed by seperate orbital energies - HOMO, LUMO, and LUMO+1 of endo are all lower in energy than the corresponding orbitals in exo. That is in accordance with expectations and was already inferred in the total energy calculation, but can be seen in the figure below in more detail.
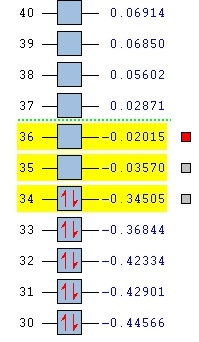 b)
b) 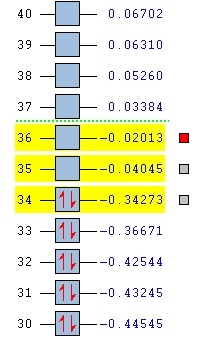
Figure 17: comparison of the orbital energies in endo (a) and exo (b)
It can be seen that all of the orbitals involved in forming the new bonds are lower in energy in the case of endo. It can therefore be argued that the secondary orbital overlap indeed plays an important role in determining the structure of the product of the Diels-Alder reaction - if we accept the fact that LUMO+1 is the orbital making the interactions and stabilising the molecule. If that is the case, then the stabilising effect of the overlap is sufficient to override the steric effects, therefore favouring the endo product over the thermodinamically favoured exo. Because of the weirdness of the results (LUMO+1 SOO instead of HOMO or LUMO playing a part), the MO calculation was repeated using the DFT level of theory.
The calculation was done on the endo structure and DFT practically yielded the same results as AM1, as shown below:
E(RB3LYP) = -612.49548420, C-C distances 2.26A, 2.26A; through space distances (maleic C - opposite C=C): 2.99A, 2.99A
That came as an unpleasant surprise - the structure of the TS is basically the same, whereas the energies differ. The C-C bond forming distanes changed slightly: from 2.16A, 2.16A to 2.26A, 2.26A, and also the through space distances were slightly elongated: from 2.89A, 2.89A to 2.99A, 2.99A. Despite that, the overall structure is effectively the same. Furthermore, the visualised MOs look the same as before - with the exception of orbitals on the C atoms that are not involved in the reaction. This shows that the method is indeed more accurate, as it takes into account more of the factors involved. However, as in the first part, it is evident that using a higher level of theory mostly only gives different energies, but the main structure remains unchanged. This is shown in the figure below.
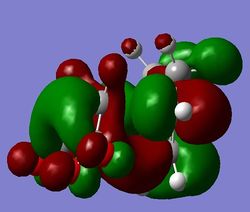 b)
b) 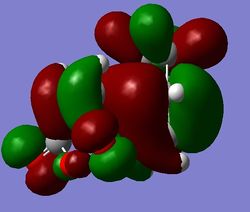 c)
c) 
Figure 18: The endo LUMO+1, HOMO, and LUMO (a), b), c) respectively), obtained with DFT.
Again, the SOO is only observed in the LUMO+1 orbital, still not in agreement with expectations. Because of the similarity of the results of endo calculations with AM1 and DFT method, DFT was not done for exo, as the result is expected to be very similar to the AM1 calculation. To conclude, this means that the SOO is, based on the results above, a vague concept, as it is not observed in the expected orbitals. It is however the only thing that was observed that could help to lower the energy of the endo transition state, hence making it the kinetically preferred product.
Despite the O.K. results (in agreement with experiments) above, it must be noted that some things have been overlooked when doing the calculations, so there is some error present in the final results. Most of those are connected to the comupational model used for carrying out the calculations. The AM1 model (Austin Model 1) is a semi-empirical method, based on the Neglect of Differential Diatomic Overlap (NDDO) integral approximation. NDDO simplifies the two-centre charge repulsions and uses the zero-differential orbital approximation. This in practice means that the number of the integrals included in the calculation where the number of particles involved is N scales with N2 instead of N4. Furthermore, a simplified version of the secular equation used in the Hartree-Fock model is employed [4], [5], [6]. Therefore, the results obtained by this method cannot be claimed to be 100 % reliable, as it is possible to arrive at different conclusions using different models (energies calculated would be different; hence the MO shapes could be different as well). The DFT method is associated with less approximations, but still does have difficulties when calculating dispersion forces and Van der Waals interactions, which could explain why the SOO effect is not seen in the HOMO and LUMO orbitals.
Conclusion
The computational experiment was successful, as we were able to identify and characterise all of the configurations of the molecules and transition states involved. For the Cope rearrangement, we were able to order in terms of energy all 10 energetically distinct ground state conformers of 1,5-hexadiene and determine that the lowest energy conformation is gauche 3. The two transition states - chair and boat - involved in the reaction were also characterised. By calculating the activation energies needed for the reaction of anti 2, it was seen that the chair conformation poses a smaller energy barrier and is hence the preferred TS. In the case of Diels-Alder reaction, we were able to minimize the energy of the transition state for a model reaction between ethene and 1,3-cyclodihexene in order to determine that the HOMO and LUMO of the TS are antisymmetric and symmetric respectively and that they are composed of the antisymmetric HOMO of the diene and LUMO of the dienophile, while the LUMO is composed of the diene LUMO and dienophile HOMO. In the further study, we have established that if there are substituents positioned on the dienophile, secondary orbital overlap (SOO) becomes an imporatant factor in determining the structure of the product. Endo structure is favoured despite being sterically more congested because of the SOO stabilisation effects. An attempt was made to improve the result using the DFT theory, but the conclusions were the same, as the difference between the results is negligible on the structural level. The results could be improved by using more advanced computational methods and theories in our calculations, as well as attempting to take more factors into account. The energies calculated and the structures identified would then resemble what really goes on more precisely, which might provide a better insight into the chemistry of pericyclic reactions.
References
1. B. G. Rocque, J. M. Gonzales, and H. F. Schaefer, Mol. Phys., 2002, 100, 441–446
2. B. W. Gung, Z. Zhu, and R. A. Fouch, J. Am. Chem. Soc., 1995, 117, 1783–1788
3. H. Rzepa, 2nd year O4 Pericyclic reactions and O5 Conformational analysis lecture notes, 2014
4. http://en.wikipedia.org/wiki/Austin_Model_1, accessed on 3rd December 2014
5. http://en.wikipedia.org/wiki/NDDO, accessed on 3rd December 2014
6. http://en.wikipedia.org/wiki/Zero_differential_overlap, accessed on 3rd December 2014
7. J. Clayden, N. Greeves, S. Warren, and P. Wothers, Organic Chemistry, Oxford University Press, New York, 2nd edition, 2012
8. P. Atkins, J. de Paula, Physical Chemistry, Oxford University Press, Oxford, 9th edition, 2010