Rep:Mod:phys3Card

The Cope Rearrangement

Conformer Analysis

In the first part of this tutorial, a range of conformations of 1,5-hexadiene were modelled and their corresponding energies calculated, initially using Hartree-Fock level of theory, and in some cases subsequently using higher level density functional theory (DFT) to fully optimise the structures. Comparisons of the structures are outlined in the following table. There are 27 possible geometric conformations, of which 10 are energetically distinct, and 8 of those are shown here. It must be said, however, that the Hartree-Fock level of theory is not realistically precise due to its lack of electron-electron correlation (which DFT does account for). Due to this, and the fact that these 8 conformers are essentially degenerate being so very close in energy, it is only valid to compare and evaluate the most and least stable structures, which is done so below. Essentially, though, there is no definitively stable conformer to be found here. (Going to arbitrarily low temperatures, can't we expect to differentiate between isomers? João (talk) 22:52, 22 December 2014 (UTC)) NB: All energies tabulated in this report are in units of Hartrees unless otherwise labelled

Moleclue Conformer	Symmetry Group	Energy - HF/3-21G / {DFT/B3YLP}	Moleclue Conformer	Symmetry Group	Energy - HF/3-21G / {DFT/B3YLP}
Antiperiplanar 1	C1	-231.690970	Gauche 1	C2	-231.687716
Antiperiplanar 2	Ci	-231.692535 / {-234.611710}	Gauche 2	C1	- 231.692661 / {-234.626455} Lowest energy conformer
Antiperiplanar 3	C2	-231.692602	Gauche 3	C2	-231.691540
Antiperiplanar 4	C2h	-231.689071	Gauche 4	C2	-231.691667

The lowest energy conformation as shown above, curiously, has a gauche linkage between the central carbons ("Gauche 2"). Given that there are no particularly favourable orbital conjugation interactions that might influence a gauche linkage, since all the orbitals are derived from either CH or CC bonds, it would be expected that the predominant lowest energy conformer would yield an antiperiplanar (APP) relationship. This is purely from steric considerations of the two C₂H₅ groups. Additionally, in reality, an APP linkage is very slightly favoured over a gauche linkage based purely on these CC and CH orbital conjugations; 19.32 kcal mol^-1 compared to 19.04 kcal mol^-1. Although all conformers are remarkably close in energy, (especially compared to the energy calculated from DFT methods) consideration of other more subtle factors can support the result of this low energy conformer.

Gauche 2: Lowest Energy

A common theme between all of the conformers is the bond angle between the 3 terminal carbons (e.g 4-5-6), on either end of the molecule, which is consistently zero. This arrangement leads to a favourable Van der Waals interaction between the 1,3-Hydrogens (e.g atoms 13 & 10), because they are now separated by a distance of 2.45 Ångströms. Since the Van der Waals radius of bonded hydrogens interacting with each other is 1.2 Å, this distance provides a favourable attraction, which quickly becomes repulsive below ~2.2 Å, as modelled well by the Lennard-Jones potential. The Dihedral Angle between atoms 2,3,4 & 5 is 66.2 degrees (as opposed to the theoretical perfect 60 degrees), which again appears to optimise the interaction between hydrogen atoms 8 & 14 at 2.6 Å (the dihedral angle of 8-2-4-14 is 0.1 degrees, thus indicating the two hydrogens in question are essentially as close as possible). This conformation also avoids the case where two hydrogens become too close, and unfavourably repel.

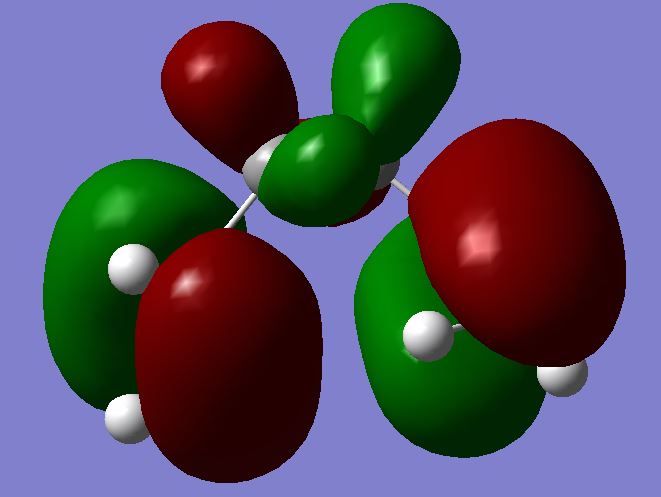
One final feature of this conformer which supports its stability is the slight conjugation derived between overlap of the two terminal π orbitals. That is, favourable delocalisation occurs between same phases of the HOMO (seen in green below). The structure must adopt a gauche form, and also a slightly skew C₁ symmetry in order to maximise this small overlap.

Lowest Energy Conformer

Low Energy Conformer HOMO

Gauche 1: Highest Energy

For comparison, a high energy conformer is shown below. As with the other highest energy conformer (Antiperiplanar 2) this one misses out on the favourable 1,3-Hydrogen interaction. It is also clear there is a substantial steric clash potential with the two termini of the molecule. For example, the H-H distance between atoms 13 and 15 is 2.3 Å, which may just be too close for comfort, and therefore repulsive. Additionally, the dihedral angle of 9-3-4-14 is only 43 degrees, which is less than the ideal 60 degree case. We can therefore infer that the two C-H sigma orbitals are slightly too close, and interact repulsively as they approach an unfavourable eclipsed conformation. The differences between these two conformations are quite subtle, even to the extent that they are hardly displaced from degeneracy. However, since they have the largest difference in energy for any two conformers it is valid to conclude that the above observations can cause the decreased stability.
The HOMO is shown below for the high energy conformer, which clearly shows no delocalising overlap between the π orbitals, as only the opposite phases are adjacent to each other.

Highest Energy Conformer

High Energy Conformer HOMO

Frequency & Activation Energy Calculation

So far, only the energy of the molecule on the idealised PES has been calculated, accounting for only the bare electronic contribution made in the bond enthalpies and such. This is not a good enough result to calculate the activation energy since the thermal and vibrionic contributions to the total energy must be considered (for the case at room temperature). These are obtained by running a frequency calculation which can be done in parallel with a normal optimisation (Rather at the end of the optimization João (talk) 22:52, 22 December 2014 (UTC)). This produces 4 different energies corresponding to various different possible energetic contributions, shown in the table below.

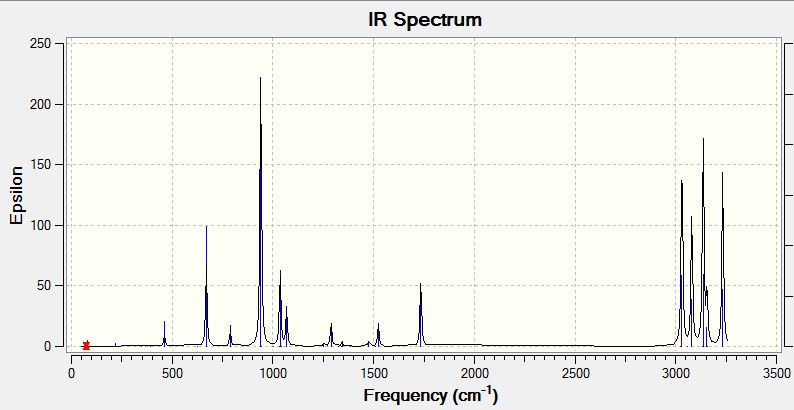
Another result of the frequency calculation is a virtual IR spectrum showing all possible vibrational frequencies. As theory predicts from the 3N-6 rule (N = number of atoms for a non linear molecule) for the number vibrational modes, there are 42 distinct frequencies for 1,5-hexadiene which contains 12 atoms. For this exercise, the frequencies of the conformer with C_i were calculated. In order to calculate the frequencies as accurately as possible, the structure of the C_i conformer is first 'fine tuned' using DFT with a B3LYP/6-31G* basis set. Additionally, this will elucidate any differences in geometry that a more accurate model might yield (What differences did you find? João (talk) 22:52, 22 December 2014 (UTC)). The C_i conformer was chosen later as the reactant for calculating the activation energy of the Cope rearrangement reaction. This is fairly arbitrary given the conformers are practically degenerate, however, the C_i structure was also incorporated into the method for obtaining the 'boat' TS. The results are as follows:

IR Spectrum for C_i Conformer

Energy Contributions	Energy - 289.15 K	Energy - 0 K
Electronic and Zero-point Energies	-234.469219	-234.469215
Electronic and Thermal Energies	-234.461869	-234.469215
Electronic and Thermal Enthalpies	-234.460925	-234.469215
Electronic and Thermal Free Energies	-234.500809	-234.469215

42nd Vibrational (sp²) Mode

Importantly, it is noted that all the 42 frequencies calculated are positive. That is, they are not imaginary (negative) frequencies that would correspond to a transition state. A particular vibrational mode is also visualised above. In order to calculate the activation energies, it is the Electronic and Thermal Energies value which is important to compare, both for the reactant molecule and the TS. This represents the minimum activation barrier for the reaction to proceed. The extra contribution taken into account here is the translational, rotational, and vibrational modes at 298.15 K and additionally 1 atm of pressure. It therefore makes sense that this value is more positive that the value from purely the PES (E_Electronic = -234.611712) since the contribution is now E_Total = E_Electronic + E_Trans + E_Rot + E_Vib. As a comparative control experiment, the various energetic contributions from the energetic modes were also calculated at 0 K. As is expected, they are all equal since there is exactly zero thermal vibronic, rotational or translational excitation here.

Transition Structure Theory

In this part of the tutorial, the theoretical transition structures for the [3,3]-sigmatropic shift of 1,5-hexadiene (i.e the Cope rearrangement) are obtained and compared. They are found using a variety of methods permissible by Gaussian, each with their own advantages. These are initially done using Hartree-Fock Theory as before, and subsequently re-optimised using DFT in order to obtain energies which can be used to more realistically calculate the activation energies for the reaction.

The two approaches here for elucidating the transition structures are quite different. The first uses an initial geometry guess supplied by programmer, who uses their chemical intuition to design what they assume is a realistic approximation to the transition state. Gaussian then optimises this guess which, if close to the truth (Truth is a very tricky word in science João (talk) 22:52, 22 December 2014 (UTC)), will yield a correct transition structure. The advantage of this method is that it theoretically starts with a good geometric guess, so the real transition structure should be found on the potential energy surface (PES) easily. The second method (QST2) simply takes a product and a reactant molecule, and attempts to interpolate between them in order to find the same point of the PES . This method may seem more computer based, taking responsibility away from the programmer, though Gaussian is only able to literally translate atoms rather than rearrange them by rotation. Thus, the initial structures for the reactant and product must be similar in geometry to the transition state (TS).

There is a third method also which simply combines the two methods above, taking 3 structures as an input, and locates the TS on the PES in the usual way. This would seem to be the most reliable, in that Gaussian has a large amount of structural information to guide along the correct path on the PES. There is also a caveat to the first method described, in that it is also possible to optimise all of the molecule apart from the bond-forming-atoms. By doing this, you may obtain a much better TS input guess for gaussian, which is more likely to yield a valid result.

In transition state theory, the TS is the maximum energy point along the reaction coordinate pathway. The difference between the initial energy of the reactant conformation and the TS energy is therefore the activation energy. On the PES itself, there are of course many other possible geometries (and therefore energies) other than those which lie along the 2 dimensional line of the reaction coordinate. As such, the PES is a surface in 3D space (Not sure what you mean by dimensions here. The PES is an hyper-surface with 3N-6 dimensions where N is the number of atoms. The reaction path is a one dimensional line in this hyper-surface João (talk) 22:52, 22 December 2014 (UTC)), upon which a saddle point represents a transition state geometry. Gaussian thus calculates the derivatives of the surface in search of this salient point corresponding to the TS. The reaction can be viewed as a trajectory along the PES, and any path which contributes to the rate constant for the reaction must pass through the narrow region of the saddle in order to react. It is also assumed that all once this point has been overcome, it is highly unlikely that the trajectory will be able to re cross the TS. However, above the idealised 0 K scenario (At 0K the only vibrational energy available is the zero point energy which would not allow the system to cross the transition state in the first place João (talk) 22:52, 22 December 2014 (UTC)), it is possible that thermally induced vibrations in the molecule give it a chance to re-cross. Therefore, it is even possible that the narrow saddle point is not the only part of the PES controlling which trajectories contribute the to rate of reaction in a thermally excited system, since they may be able to bypass it entirely.

Chair Transition Conformation

The Cope rearrangement proceeds via a conformation resembling one of cyclohexane's two most stable structures; a 'boat' or a 'chair'. The first attempt was aimed at the chair structure, which has perfect C_2h symmetry. This specific symmetry label, which Gaussian can detect, can indicate whether or not the correct structure has been reached. Although the guidelines suggested to first optimise allyl C₂H₅ fragments, Gaussian would not allow such an electronically deficient structure. Instead, a standard propene was optimised (Not sure what you mean: Gaussian can in principle find the electronic energy for a species with an arbitrary number of electrons, and propene does not have the chemical formula C₂H₅ João (talk) 00:59, 23 December 2014 (UTC)), replicated, and the two oriented roughly in a chair conformation. Using this as estimated input, a tandem optimisation (to a TS not a minimum) and frequency calculation was run. It is crucial to do both, since the presence of a negative frequency in the virtual IR spectrum directly implies a TS has been reached. Additionally, it is important to tell Gaussian to calculate the force constant matrix, since it is necessary to obtain the curvature of the PES in order to guide the trajectory 'upwards' energetically.

Luckily, the initial guess was close enough to yield a successful TS:

Structure	TS Vibration	Energy - HF/3-21G	Energy - DFT/B3LYP	TS Frequency - HF/3-21G	TS Frequency - DFT/B3LYP
Chair TS		-231.619322	-234.556931	- 818 cm-1	-569 cm-1

Three results from this calculation quantitatively conclude that the correct TS has been found. The most pertinent indicator is the negative frequency which both DFT and HF theory predict, albeit at significantly different values. The second significant indicator is the C_2h symmetry label which Gaussian assigned the structure without prompting, at a high tolerance (0.01). Thirdly, although not definitive, the simple fact that the energy returned by the HF calculation is higher than all of the initial 8 conformations of 1,5-hexadiene supports the same conclusion. Clearly, the TS should be higher in energy as it is unstable. A qualitative piece of evidence which Gaussian also predicts, is the vibration modelled in the table, corresponding to the imaginary frequency. This vibration, interestingly, agrees with what chemical intuition would predict. That is, one bond is breaking between the third and fourth carbon, and another forming between carbons one and six in a concerted asynchronous fashion.

The other method of using the redundant coordinate method was also attempted. This freezes the sigma bond forming & breaking atoms (i.e carbon atoms 3 & 4 and 1 & 6) while optimising the remainder of the system. Gaussian then calculates the force constants in the direction of the bond coordinates to seek the TS. Unfortunately, it did not yield the TS found in the first successful attempt (What happened? What was different? What was the error? João (talk) 00:59, 23 December 2014 (UTC)). The reason for this in unclear, but it could have potentially been because the length at which the bonds were chosen to be frozen, 2.2 Å, left the structure too distant from the TS on the PES. Thus, Gaussian was not able to find it. In the successful attempt, the partially formed sigma bond length was 1.97 Å, which could support why this method failed.

Boat Transition Conformation

This was optimised quite laboriously, using the QST2 method using two input files between which Gaussian interpolates as described above. The C_i conformer was used for both the reactant and product inputs. It was quite difficult to assign the correct numeric labels to both molecules so that they matched, but the method has potential to be powerful since the program knows exactly where the start and end points are. The particular setup detailed below, however, is doomed to fail because Gaussian does not consider to do anything but a direct translation of the correct atomic groups. The invalid result is shown below:

Input Structures	Output
thumb	Boat Failed TS

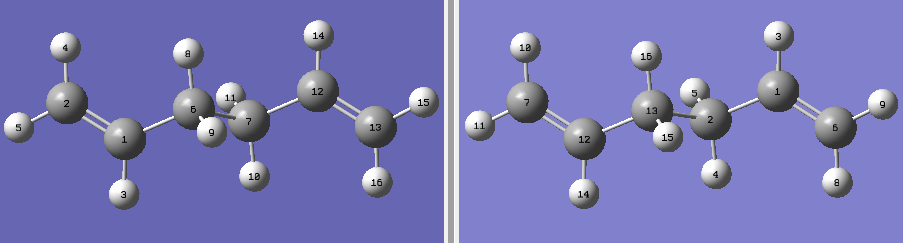The reason why the above structure is deemed incorrect is because the partial sigma bonds represented by the dashed lines cross over each other. Clearly, bonds cannot cross in such a fashion (The dashed lines have no meaning: what counts in a quantum mechanical calculation is the inter-nuclear distance, the rest is just a drawing. Indeed you get a perfectly normal chair transition state. João (talk) 00:59, 23 December 2014 (UTC)). More significantly, the structure has also predicted a chair conformation again, rather than a boat. This is a result of the fact that Gaussian knows which bonds should join, but doesn't allow the correct rotation which would align them properly. However, even though the result is easily disregarded, ignored the somewhat arbitrary partial bond lines, the geometric position of the atoms is actually relatively accurate. The distance between the atoms forming the new sigma bond is 2.02 Å compared to the previous, correct, chair TS whose bond distance in the same location is 2.20 Å.

Input for Boat QST2

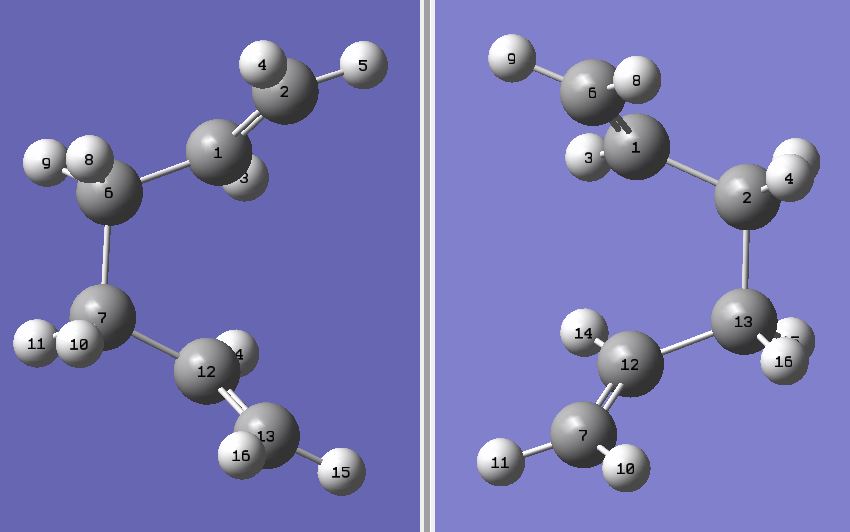
In order to obtain a valid boat TS, the C_i conformer was simply twisted so that the central dihedral angle was changed from 180 to 0 degrees. This input structure is closer in geometry to the desired boat TS structure, and is therefore much easier for Gaussian to handle. As with the chair conformer, the presence of a C_2v symmetry label from Gaussian indicates that the correct TS has been found (If the two fragments were 10Å apart would the symmetry group be different? Would you have the "correct" transition state structure? João (talk) 00:59, 23 December 2014 (UTC)). The full results are shown below:

Structure	TS Vibration	Energy - HF/21G	Energy - DFT/B3LYP	TS Frequency - HF/21G	TS Frequency - DFT/B3LYP
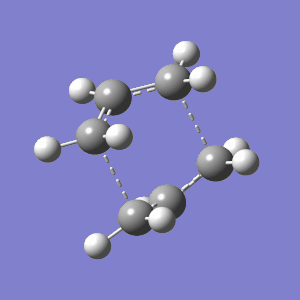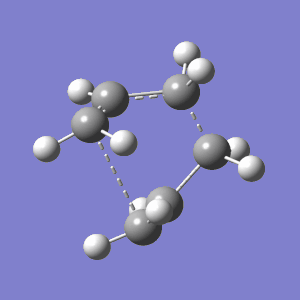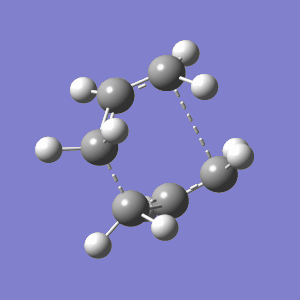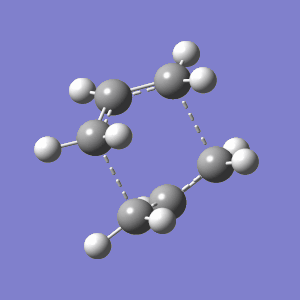Successful Boat TS		-231.602802	-234.543078	- 840 cm-1	-532 cm-1

Again, these results quantitatively conclude that the correct boat TS has been located. The correct C_2v point group was assigned by Gaussian, negative frequencies were assigned to the asynchronous transient vibration shown above, and the HF energy is slightly higher than that of all the 1,5-hexadiene conformations. It it also interesting to note that the energy for the boat TS is slightly higher than that for the chair ( -231.602802 compared to -231.619322). This is an intuitively predictable result when compared to the analogue of simple cyclohexane which, although fully bonded in a ring, adopts a chair as its definitively stable conformer, with the boat its next most stable.. Moreover, although the precise mechanism for the transition is in dispute, it is well established that the TS does indeed travel through the aromatic C_2h chair conformation from extensive computational research.

Intrinsic Reaction Coordinate

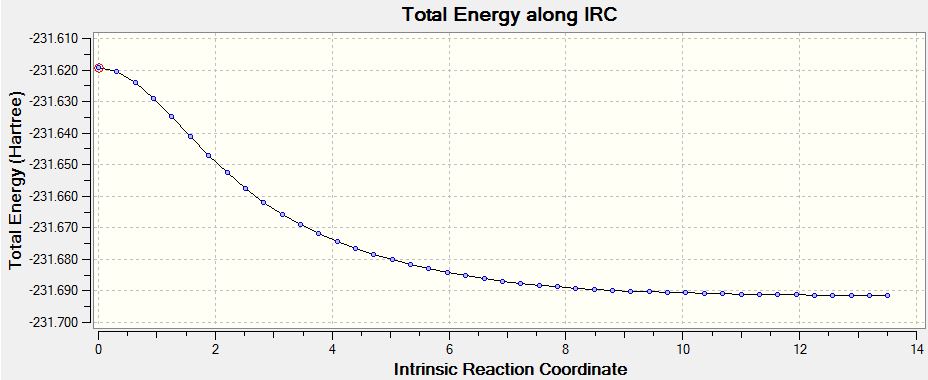
The final question relates to which conformations these reactions would naturally fall to, and which would be the most likely precursors. The latter is almost impossible to answer, since all the conformations are practically degenerate, as demonstrated initially. For the same reason, it is also slightly invalid to say that the reaction will preferentially return to a particular conformer in this scenario (Wouldn't that depend more on the energy barrier between conformers? João (talk) 00:59, 23 December 2014 (UTC)). However, Gaussian has a method which will attempt to work this out, as it is able to run an intrinsic reaction coordinate (IRC). This essential does the same as a minimisation optimisation, but records each step along the way. This was carried using the optimised C_2h chair transition structure as the starting point. The result is shown below:

IRC Path	Final structure	Final Energy - HF/21G
	Final IRC prediction	-231.691579

The IRC correctly minimised the TS to a valid end point which is on the cusp of converging absolutely, and is clearly approaching the C₂ "Gauche 4" conformer which is tabulated at the start. Even after 43 steps, however, the energy does not quite match the original which was calculated at -231.691667 Hartrees. It would of course be possible to take the final structure and minimise in the usual way, and the result would precisely match that calculated for the Gauche 4.

Activation Energies

All that is left to find is the activation energy for the Cope rearrangement. As outlined before, this will be done by finding the thermally corrected values of the systems, technically named the Electronic and Thermal Energies. This includes energetic contributions from all possible vibronic modes of movement. The results are tabulated below and compared to experimental values. The activation energies have been calculated using only the DFT B3LYP/6-31G* results and the Electronic and Thermal Energies, and therefore correspond to a reaction at 298.15 K:

{HF/3-21G} B3LYP/6-31G*

	Electronic Energy	Electronic and Thermal Energies	Activation Energy / kcal mol-1	Activation Energy (Literature) / kcal mol-1
Chair TS	{-231.619322} -234.556931	{-231.461336} -234.408980	33.188	33.5 / 33.8
Boat TS	{-231.602802} -234.543078	{-231.445305} -234.396007	41.329	44.7
Reactant (APP 2; Ci)	{-231.692535} -234.611710	{-231.532573} -234.461869

(How did the transition state geometries compare at the two levels of theory? After re-optimization with DFT, was one imaginary frequency still observed? João (talk) 00:59, 23 December 2014 (UTC))

The Diels Alder Cycloaddition

In this section, the transition structures for two Diels Alder cycloaddition reaction will be investigated. Namely, the reaction of butadiene with ethene, and the reaction of maleic anhydride with cyclohexa-1,3-diene. The first is the simplest possible type of reaction, and will outline the theory and reactivity of this reaction. The second example demonstrates increased reactivity due to a very favourable electronic orbital matching demand, and also presents two possible transition structures,EXO and ENDO, which will be examined and contrasted. As the methodology was detailed greatly in the previous section, this will be taken for granted in the following analysis, apart from specific changes, and instead will focus more of orbital interaction and mechanistic details.

Butadiene + Ethene

Butadiene + Ethene

This reaction is a pericyclic reaction which undergoes an aromatic transition state, catalysed by thermal excitation. In order to react, the correct orbital alignment and symmetry is absolutely crucial. Clearly, the molecules must be in the correct conformation to begin with, since only cis-butadiene orients the diene correctly for the ethene to attack. Moreover, the symmetry of the HOMO of one reactant must match the symmetry of the LUMO of the other, and vice versa. The normal electronic demand for Diels Alder reaction is to have an electron deficient dienophile and and electron rich diene. This normal demand is particularly apparent in the second example involving maleic anhydride. The electron rich diene therefor has a higher energy HOMO than the dienophile, and the upshot is that it is this diene HOMO that interacts with the dienophile LUMO. The symmetries of these must be alike, so they are compared below. (In the optimisation calculations, a semi-empirical method was used with AM1 basis set)

	Butadiene	Ethene	TS - Towards Cyclohexene
HOMO	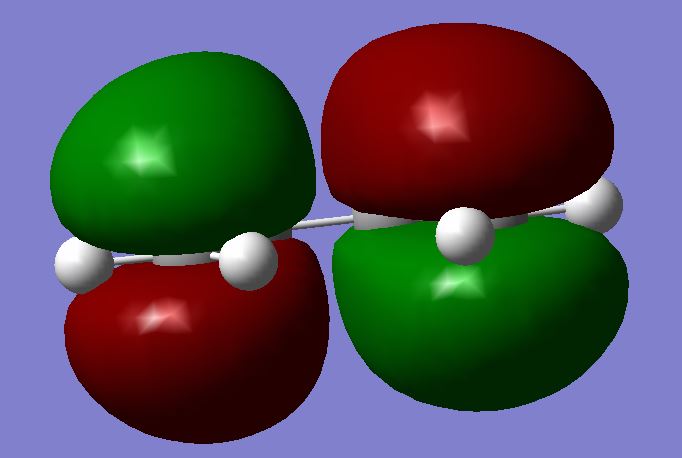Antisymmetric	Symmetric	Symmetric
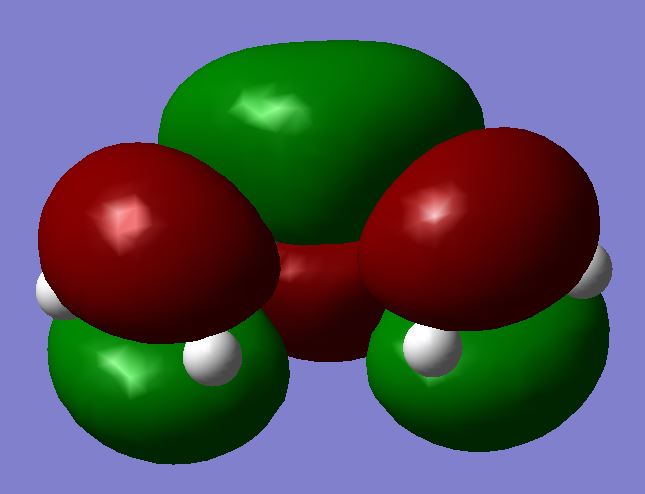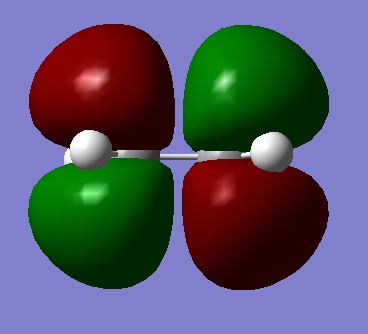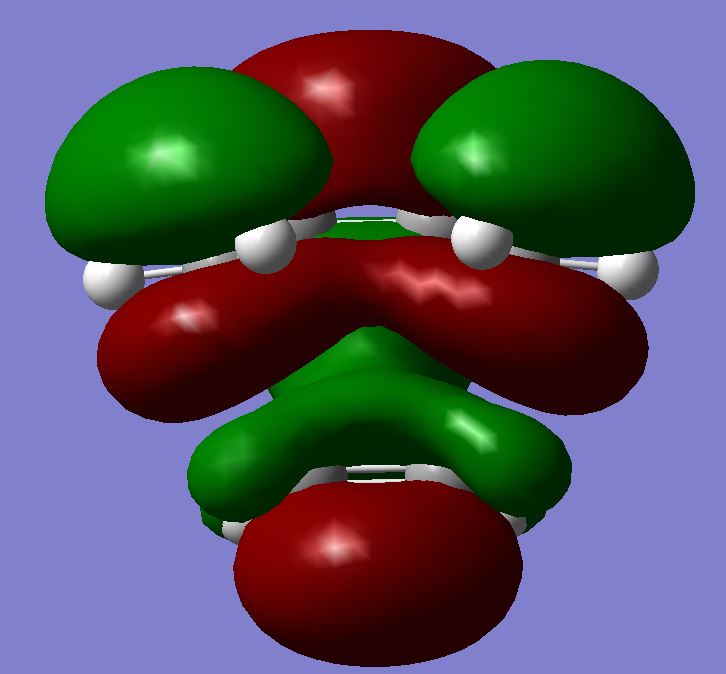LUMO	Symmetric	Antisymmetric	Symmetric

It is clearly seen that the symmetries match, which diagonal relationships above. The butadiene HOMO and the ethene LUMO are both antisymmetric with respect to the plane cutting perpendicularly through the centre of each molecule. The other relationship matches the butadiene LUMO and the ethene HOMO as symmetric. As such, the resulting HOMO of the adduct, cyclohexene, should also be antisymmetric if normal electron demand were to follow. There is only one possible conformation of the TS due to the high symmetry of each of the reactants. Curiously, however, it is noted that both the HOMO and the LUMO of the TS are symmetric. The only explanation for this is that the LUMO of butadiene has interacted with the HOMO of Ethene (Did you look at the HOMO-1 of the transition state? João (talk) 00:59, 23 December 2014 (UTC)). This corresponds to inverse electron demand, which typically only exists for the case where the diene is electron deficient. This seems to imply that ethene here is electron rich in comparison to butadiene. This reaction is still allowed, however, as it does not break any symmetry rules, and still proceeds suprafacially with dis-rotation of the orbitals involved, thus travelling through a Hückel aromatic transition state. Further elucidative information about the TS is shown below:

TS - Cs Symmetry	TS Imaginary Vibration	TS Lowest Frequency	Energy (HF/3-21G)	Partial σ bond length
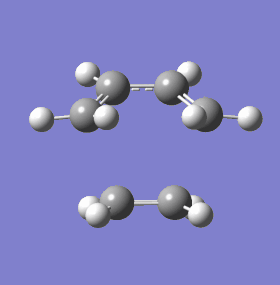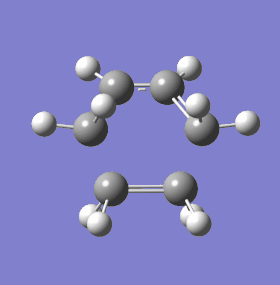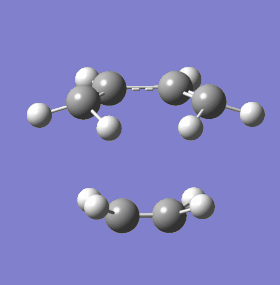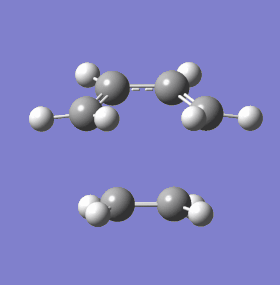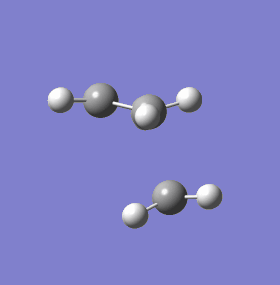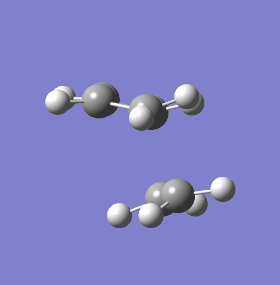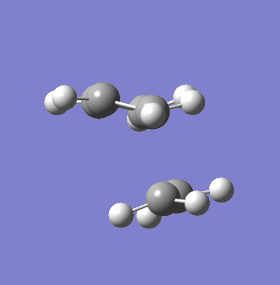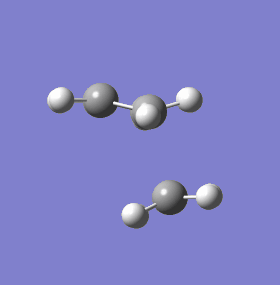Diels Alder TS	Frequency = -818 cm-1	Frequency = 167 cm-1	-231.603208	2.21 Å

The geometry of the TS is shown above, only without its symmetric orbitals in place. The definitive indicator of a TS is again given by Gaussian, as a negative frequency. This shows a synchronous forming of two new sigma bonds. This fits well with the general hypothesis that pericyclic cycloaddition reactions (and all pericyclics in general) take place in a totally electronically concerted fashion, with both bonds forming at the same time. As a contrast, the next lowest positive frequency is shown also. In stark contrast to the vibration indicative of a TS, the vector of vibration runs perpendicular to the alignment of orbital interaction. In other words, this vibration imposes no energetic (or at least very little) change in the system, since the overlap of orbital is hardly affected. With the synchronous bond forming vibration, it is clear that the orbital overlap between the HOMO / LUMO will increase dramatically as the bond forming atoms approach one another.

The equilibrium bond length of the partial σ bond is also shown, to compare to the standard (non aromatic) sp² and sp³ C-C single bond lengths, which are 1.46 Å and 1.54 Å respectively. Cleary then, the TS is still some way towards forming full sp³ C-C bonds as they would be in cyclohexene. To conclude, this reaction appears to have at least started along the the inverse election demand path, given that the final orbitals for the TS are symmetric which can only be explained with the two symmetric orbital's interaction (the diene LUMO and the dienophile HOMO).

Maleic Anhydride + Cyclohexa-1,3-diene

Here, it is quite clear without having to calculate the arrangement of the HOMO / LUMO for either molecule that this is a typical case of normal electron demand. This conclusion is obvious since the two carbonyls, both alpha to the dienophile's functional π system, are extremely electron withdrawing. This has the effect of both making the dienophile electron deficient and giving it a low energy HOMO and LUMO. Additionally, the alkyl cyclic chain on the cyclohexa-1,3-diene serves as a mild electron donating group.

It is also worth mentioning that the TS was a lot more difficult to obtain for this larger system. The precious method of estimating the TS manually does not appear to give an accurate enough input for Gaussian. The tolerance on the symmetry of the input seems to be much greater. To overcome this, each reactant was optimised individually and forcefully symmetrised to give a C_s point group which is the point group for the target TS. The two were then joined, again forcefully symmetrised by Gaussian, and set to optimise to a TS in the usual way. For the EXO TS state this method worked well. For the ENDO, only the redundant coordinate method appeared to yield a correct answer, again showing a very tight tolerance for the input structure. So, although thermodynamically this reaction would appear very reactive due to the very favourable electron demand, perhaps the kinetic reactivity is somewhat hindered since a very specific conformation must be obtained for a successful reaction.

All of the structures and MOs were calculated using DFT/6-31G* since the AM1 semi empirical method consistently failed in producing the correct TS. Additionally, for the sake of consistency, since DFT was used to calculate the activation energy in the tutorial, and it is more accurate, the same is done here. The same set of HOMO / LUMO diagrams is outlined below for this new system:

	Maleic Anhydride	Cyclohexa-1,3-diene	TS EXO	TS ENDO
HOMO	Antisymmetric	Antisymmetric
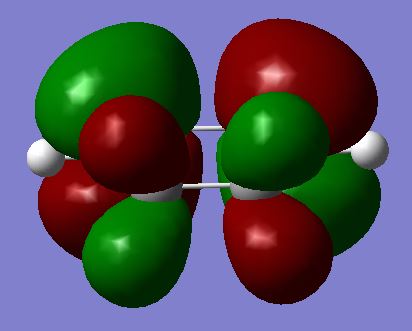LUMO	Antisymmetric	Symmetric

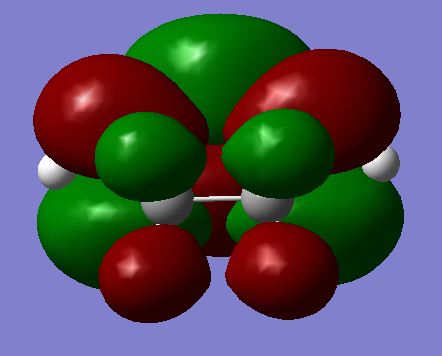As before, it is certain that a TS has been reached given the quantitative information that Gaussian provides; the negative frequency, the increased energy compared to the reactants, and the correct symmetry label (C_s). It is clear from this that the only two frontier MO which will be able to interact are the maleic anhydride LUMO and the Cyclohexa-1,3-diene HOMO, since only this pairing matches symmetry (both antisymmetric). This is an interesting observation, because based on the idea of the strong normal electronic demand of this system, the only practically viable reaction is also for this particular HOMO / LUMO pairing to interact. The interest lies in the fact that the converse HOMO / LUMO is actually forbidden by symmetry rules, so is not just unlikely, but will not happen. It would be impossible for an anti HOMO to interact with a symmetric LUMO.

As expected and illustrated above, all four of the HOMOs and LUMOs for both the EXO and the ENDO are also antisymmetric (Did you expect this a priori? Did you expect to have a σ HOMO for maleic anhydride? Could the frontier orbital idea be misplaced here? João (talk) 00:59, 23 December 2014 (UTC)), which backs up the prediction for which pairing should interact. These two possible configurations of the TS are also plotted above. The difference is simply a 180 degree rotation for one of the molecules in relation to another. The result is a very slightly more stable form, named the ENDO. This is thought to be due to an effect called secondary orbital overlap. This, however, cannot be seen on either the HOMO or the LUMO (although it would surely only provide stability in the HOMO anyway). This is quite certain, as it can be clearly seen that a nodal plane exists between the two molecules in both of the LUMOs for the TSs, and the only orbital overlap present in the HOMOs is that of the σ bond which is about to form. Even though it does not appear where expected, a secondary orbital overlap can be observed in certain regions:

ENDO LUMO + 1

The above shows a clear orbital overlap, but rather than being between the partially formed σ bond, it is between the carbonyls on the maleic anhydride and the π system on the diene (shown in red). These would be the expected orbitals for secondary overlap, and they demonstrate it well here. It doesn't behave in a way such that any new bonds will be formed, or even partial bonds, but it does serve to stabilise the overall structure, in theory. Having said that, the fact that this overlap is only observed in the LUMO + 1 makes it seem very unlikely that it will provide any stabilisation at all, since it contains no electrons, and so can't exploit this orbital delocalisation. Thus, it is reasonable to conclude that no stabilisation is derived from this apparent secondary overlap. (You discuss the interaction with the carbonyls' anti-bonding orbital. One could check if the interaction with the corresponding orbital is stabilizing João (talk) 00:59, 23 December 2014 (UTC))

There is another interesting caveat which became apparent when comparing the MO diagrams for different levels of theory, which may actually contradict the dismissive conclusion above:

DFT MO (left) compared to AM1 MO (right)

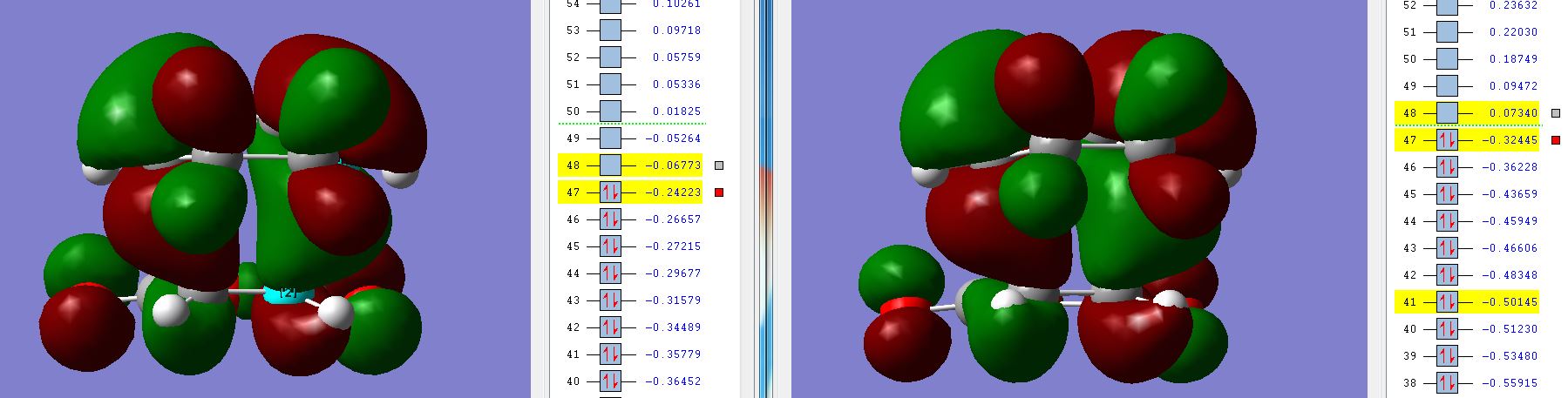
This result is quite intriguing when you examine the DFT MO in particular, the level of theory with which all of the structures and energies were calculated. It is not the first time that DFT has given starkly different information. For example, the imaginary frequencies for the Cope rearrangement TS were wildly different compared to HF. It has been said that DFT gives the wrong orbitals, however the above scheme may be supportive evidence for stabilising secondary orbital interaction. It can seen that the green dotted line marks the boundary between negative and positive MOs, which, as one would expect, is between the HOMO and LUMO for AM1. For the DFT MOs, the line appears above the LUMO + 1, which means that this orbital is negative in energy and therefore if it were to contain electrons would provide stabilisation. This result means that if, somehow, a pair of electrons were able to be delocalised into this orbital from the rest of the molecule, a stabilising secondary orbtial overlap would indeed be present. This is feasible given the opportunity for thermally induced vibrations which break symmetry and re-position orbitals. This effect would go some way to explaining why the ENDO form is slightly lower in energy than the EXO. (How about steric effects? João (talk) 00:59, 23 December 2014 (UTC))

A final table detailing the energies of each of the components, including their thermal vibronic contributions at 298.15 K, is shown below. As predicted, the energy of the ENDO is lower, and so therefore is the activation energy required to reach this configuration. This means that the ENDO product would be kinetically favoured, and therefore at low temperatures would form a majority product over EXO. As before, the energies have been calculated using the Electronic and Thermal Energies values and DFT/ B3LYP 6-31G*.

	Electronic Energy	Electronic and Thermal Energies	Activation Energy / kcal mol-1
ENDO TS	-612.683396	-612.491838	15.848
EXO TS	-612.679335	-612.487669	18.464
Reactants Combined	-612.70541471	-612.517094	n/a