Rep:Mod:pg1910x
The goal of this page is to serve as a record and as a means to explore and understand the steps and processes under taken as part of year 3 inorganic computational lab. Using computational software such as Gaussian to model simple molecules such as BH3. to then see the effect that changing either the boron or hydrogens, or both has on how the overall system behaves.
Optimising BH3
|
Optimisation of a simple molecule, BH3
|
Item Value Threshold Converged?
Maximum Force 0.000014 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000073 0.001800 YES
RMS Displacement 0.000048 0.001200 YES
Predicted change in Energy=-1.594082D-09
Optimization completed.
-- Stationary point found.
|
The system was originally set up with a triginal planar molecule with a boron atom situated in the center and three Hydrogens at the points.
Optimising GaBr3
|
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.282683D-12
Optimization completed.
-- Stationary point found.
|
Mixing Basis sets and Pseudo-potentials
|
Item Value Threshold Converged?
Maximum Force 0.000029 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000109 0.001800 YES
RMS Displacement 0.000067 0.001200 YES
Predicted change in Energy=-3.046496D-09
Optimization completed.
-- Stationary point found.
|
What does it mean?
| Molecule | Bond Length ( ) |
|---|---|
| BH3 | 1.192313267 |
| BBr3 | 1.9339639 |
| GaBr3 | 2.3501818 |
When Hydrogen is replaced with Bromine, the major change that will effect bond length is the atomic radii of the atoms (25-115 pm[citation needed]), while hydrogen has just a proton and its electron, Bromine not only have a nuclei 80 times more massive, but more importantly has 3 fully filled shells, a fully occupied 4s and 3d and partially occupied 4p orbital this means that the repulsion between the atoms is felt at a greater distance and that the orbital overlap is much worse leading to an reduced attractive force in the the σ
bond, there is however an additional interaction that the bromine will have with boron that hydrogen will not. This will be a π interaction between the electrons in bromine 4p orbitals that align with the vacant p orbital of boron.
A similar effect can be seen when comparing BBr3 and GaBr3, however the central atom is being changed in this case. The atomic radii is increasing from 85 pm to 130 pm[citation needed], and while the orbitals will have a better overlap, they are also becoming more diffuse so both the σ and π interactions will become weaker
Boron and Gallium can both be found in group 13 of the periodic table, in the monomeric form or their trihydrides will form a trigonal planar structure with a vacant p orbital perpendicular to the plane of the molecule. This orbital is capable of acting as a lewis acid to complete the valence shell of the molecule. Going from Boron down to Gallium, atomic radius and electron count increases and electronegativity decreases, this will generally lead to the formation of weaker bonds.
A bond can be thought of as a system in which two distinct particles interact in such a way as to reduce their overall energy to a minimum. Bonds consist of two ... parts, the first in an attractive interaction where the nuclei of one atom interacts favorably with the electrons of the other atom, the other part is the repulsion felt at the distance between the two atoms reduces until the nuclei of the two atoms start to interact repulsively. the two parts have different distance dependance and act over different ranges. The result is that the system will sit in an energy well where the attractive and repulsive terms cancel one another out.
Gaussview uses a proximity based rule to show bonds when visualising the molecule, when two atoms come in close enough proximity to one another is will show up as a bond
Frequency Analysis for BH3
| File Name | PG_BH3_freq |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532356 a.u. |
| RMS Gradient Norm | 0.00000891 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0001 Debye |
| Point Group | CS |
| Job cpu time: | 0 hours 0 minutes 32.0 seconds. |
| File | File:PG BH3 freq.log |
Low frequencies --- -26.9662 -12.4143 -5.8432 -0.0007 0.0006 0.0010 Low frequencies --- 1162.9038 1213.0582 1213.1931
Due to the lower frequencies falling out of the ±15 () range the symmetry was constrained, re-optimised and the frequency analysis run again. As can been seen bellow, the low frequencies fall with in the the range required to be able to say that a minimum energy has been reached.
|
|
Low frequencies --- -0.8755 -0.6666 -0.0055 7.4222 12.6420 12.6723 Low frequencies --- 1163.0035 1213.1874 1213.1901
| Mode | Sym. Lable Frequency (Hz) IR Intensity |
Motion | |
|---|---|---|---|
| 1 | A2" 1163.00 92.5475 |
 |
This vibration is an out of plane vibration of the molecule, akin to the wagging motion seen in H2O |
| 2 | E' 1213.19 14.0555 |
 |
These two vibrations have the same energy so would give overlapping peaks on an Infrared spectrum. |
| 3 | E' 1213.19 14.0591 |
 |
|
| 4 | A1' 2582.25 0.0000 |
 |
This is a totally symmetric vibration, and as such will have no change in dipole necessary to be visible in the Infrared spectrum. |
| 5 | E' 2715.42 126.3310 |
 |
These two are degenerate so will give overlapping peaks. |
| 6 | E' 2715.42 126.3215 |
 |
blah blah blah
Frequency analysis of GaBr3
|
|
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
| Sym. Lable Frequency (cm-1) IR Intensity |
Motion | |
|---|---|---|
| 1 E' 76.3744 3.3447 |
 |
|
| 2 E' 76.3753 3.3447 |
 |
|
| 3 A2" 99.6982 9.2161 |
 |
|
| 4 A1' 197.3371 0.0000 |
 |
|
| 5 E' 316.1825 57.0704 |
 |
blah blah blah |
| 6 E' 316.1863 57.0746 |
 |
blah blah blah |
Comparing the vibrations of BH3 and GaBr3
|
As both of the molecules have the same symmetry you don't see a change in the number of bands seen in the IR spectrum. One thing that can also be seen from the table is that the orders of the energies of a particular vibrations have changed order, this can be explained by considering how the mass within the molecule is distributed. In BH3 most of the mass is contributed by the boron atom, which sits in the centre of the molecule whilst the small and light hydrogens move around it. In GaBr3 most of the mass it contributed by the three bromines (M(Br)>M(Ga)) whilst the lighter gallium is situated in the centre. This is seen mostly in the A2" symmetric stretch where all three of the outside atoms move together in one direction whist the central atom moves in the opposite direction. What we see is that when the mass in concentrated in the outside the molecule the vibrations becomes a lot less energetic.
|
You need to use the same basis sets when comparing different properties of molecules because you need to have the same model being used for the electrons in the molecule, otherwise you can get drastically different results.
A frequency analysis allows us to calculate the IR spectrum of the molecule, model the vibrations that it undergoes and tells us how converged the optimisation calculation was.
The low frequencies represent the convergence of the optimisation calculation.
MO orbital analysis of BH3
Energy calculation for BH3 can be found in the D-Space link below [| D-space]
Seen bellow is a diagrammatic representation of the MO diagram of BH3 and the atomic orbitals that contribute to the MOs that are calculated.
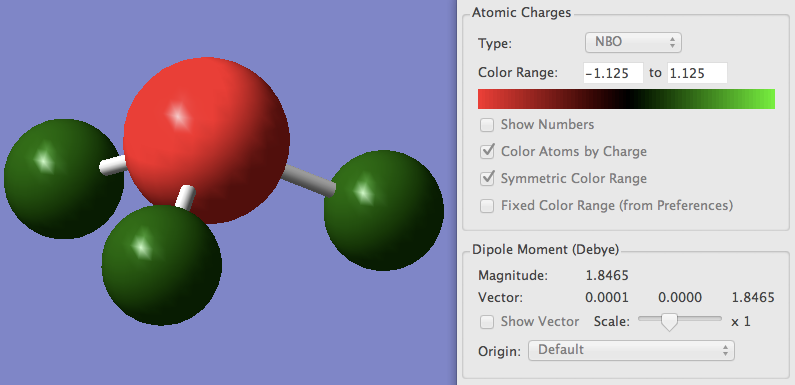
Analysis of NH3
| NH3 Optimisation symcon | |
| File Name | PG_NH3_OP_symcon3_log_86093 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -56.55776872 |
| RMS Gradient Norm | 0.00000136 |
| Imaginary Freq | |
| Dipole Moment | 1.8465 |
| Point Group | C1 |
| Job cpu time: | 0 days 0 hours 0 minutes 31.3 seconds. |
| File | File:PG NH3 OP.log |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000008 0.000060 YES
RMS Displacement 0.000004 0.000040 YES
Predicted change in Energy=-1.763364D-11
Optimization completed.
-- Stationary point found.
Low frequencies --- -9.2630 -8.2101 -6.4598 0.0003 0.0009 0.0017 Low frequencies --- 1089.3338 1693.9209 1693.9243
******************************Gaussian NBO Version 3.1******************************
N A T U R A L A T O M I C O R B I T A L A N D
N A T U R A L B O N D O R B I T A L A N A L Y S I S
******************************Gaussian NBO Version 3.1******************************
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
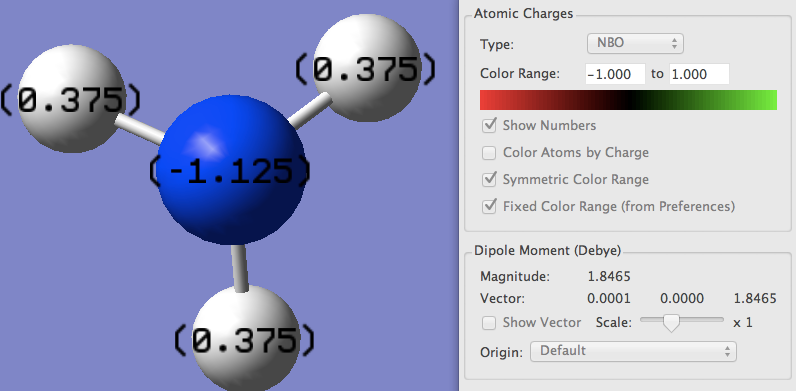
N 1 -1.12514 1.99982 6.11103 0.01429 8.12514
H 2 0.37505 0.00000 0.62250 0.00246 0.62495
H 3 0.37505 0.00000 0.62250 0.00246 0.62495
H 4 0.37505 0.00000 0.62250 0.00246 0.62495
=======================================================================
* Total * 0.00000 1.99982 7.97852 0.02166 10.00000
Natural Population
--------------------------------------------------------
Core 1.99982 ( 99.9908% of 2)
Valence 7.97852 ( 99.7315% of 8)
Natural Minimal Basis 9.97834 ( 99.7834% of 10)
Natural Rydberg Basis 0.02166 ( 0.2166% of 10)
--------------------------------------------------------
Atom No Natural Electron Configuration
----------------------------------------------------------------------------
N 1 [core]2S( 1.53)2p( 4.58)3p( 0.01)3d( 0.01)
H 2 1S( 0.62)
H 3 1S( 0.62)
H 4 1S( 0.62)
Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
-0.0001 -0.4986 -0.0059 0.0000 0.0000
0.0000 0.8155 0.0277 -0.2910 0.0052
0.0000 0.0000 0.0281 0.0087 -0.0014
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0000 0.0000 -0.0289 0.0072
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 -0.7062
-0.0240 0.4078 0.0138 0.2910 -0.0052
-0.0076 -0.0243 0.0140 0.0044 0.0014
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 0.0250 -0.0145 -0.0072
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.7062
0.0240 0.4078 0.0138 0.2909 -0.0052
0.0076 0.0243 0.0140 0.0044 0.0013
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0250 -0.0145 -0.0072
NH3BH3 analysis
| File Name | PG_NH3BH3_OP_log_86106 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -83.22468905 a.u. |
| RMS Gradient Norm | 0.00000049 a.u. |
| Imaginary Freq | |
| Dipole Moment | 5.5646 Debye |
| Point Group | C1 |
| Job cpu time: | 0 days 0 hours 3 minutes 31.9 seconds. |
| File | File:PG NH3BH3 OP.log |
Low frequencies --- -2.3973 -2.1481 -0.0016 -0.0015 -0.0009 2.6916 Low frequencies --- 263.4474 632.9795 638.4324 |
Energy of association...
E(NH3) = -83.22468905 au
E(BH3) = -56.55776872 au
E(NH3BH3) = -26.61532355 au
ΔE = -26.61532355-(-56.55776872-83.22468905) = -0.05159678 au = -135.47 kJmol-1
This large exothermic value means that the NH3BH3 molecule is much more stable than NH3 and BH3 individually.