Rep:Mod:pg1910w

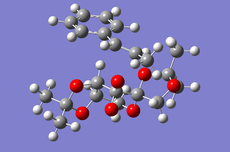
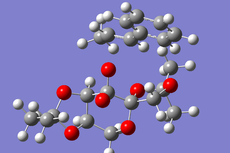
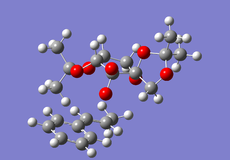
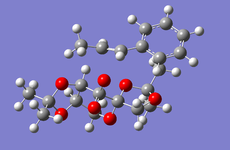
Cyclopentadiene Diemerisation

Energies of Cyclopentadiene and their dihydro compunds

Energy	Structure 1 (Exo)	Structure 2 (endo)	Structure 3	Structure 4
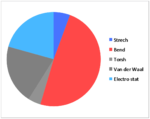
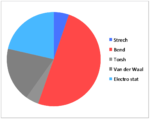
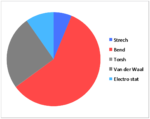
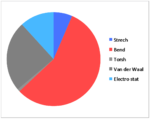
Strech	14.834	14.517	13.849	11.820
Bend	128.839	138.965	129.212	103.352
Torsh	-11.434	-12.349	0.272	-1.584
Van der Waal	53.598	51.739	55.595	44.536
Electro stat	54.486	59.387	21.441	21.550
TotalE	231.838	243.633	212.366	172.737
File	File:PG CPD S1.txt	File:PG CPD S2.txt	File:PG CPD S3.txt	File:PG CPD S4.txt

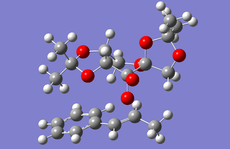
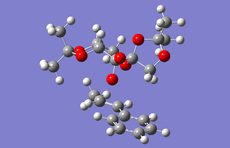
Above is the table showing the energies of the cyclopentadiene dimer in its Exo (S1) and Endo (S2) form and then two different singly hydrogenated molecules. What we see initially from the MMFF94s calculations when comparing the Exo and Endo structures is that the Exo (S1) structure is Lower in energy than the Endo form. This energy difference is seen in the energy of the bending term of the calculations indicating that the Endo structure is bent from ideality.

As experimental results show that the Endo structure is almost exclusivly produced, we can state that while the Exo is thermodunamically favored, it is not the kinetic product. This can be explained by that fact that when the rings overlap to react, the π-systems can interact during the transition state leading to a stabilisation of the transition state.

Depiction of orbital overlap, and energy surface

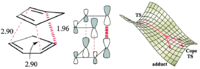
An attempt to model the TS of the Endo reaction was meet with almost overwhelming failure. As is discussed in the blog of Professor Henry Rzepa, the computer model struggles because the bond formation occurs asynchronously and once one of the bonds have formed there are two possible routes available for the reaction to take. On top of this reaction in question is electrocyclic requiring the contribution of _π2_s electrons from one system and _π4_s electrons from the other. but when the two systems involved have the same properties then the calculation struggles to decide where the electrons should come from. Others have had more success in calculating the endo transition state, it was seen by them that far from being a synchronous process, there are in fact two transition states with the two bonds forming separately, if there is time, it is hope to take the transition state calculated (where only one bond formed) and but it back into the calculation to see is a second TS can be found

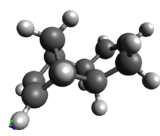
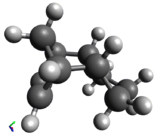
Hydrogenation of the dimer gives you either S3 or S4 dihydro compounds. When their energies are compared we see that S4 is significantly more stable then S3 the to main contributing factors are the bending energy and the van der waals energy. The greater bending energy in S3 is likely due to the constrained double bond, while the reduced vander waals energy of S4 is likely due to a through space interaction of the alkene with a nearby hydrogen

Taxol Confimers

Shows Difference from lowest energy conformer

Energies of the different possible taxol conformers

											height=160|
	TaxOdHu_Chl	TaxOdHu_Chr	TaxOdHu_TBr2	TaxOdHu_TBr	TaxOuHu_Chl	TaxOuHu_Chr	TaxOuHu_TBl	TaxOuHu_TBl2	TaxOdHu_Hin_Chl	TaxOuHu_Hin_Chl	TaxOuHu_Hin_TBr
BOND STRETCHING	36.020	31.820	32.735	32.391	32.102	35.563	33.308	33.521	67.221	57.047	62.643
ANGLE BENDING	90.786	78.712	88.672	82.067	118.391	140.823	124.422	126.597	202.400	191.043	256.053
STRETCH BENDING	-0.846	-0.598	-0.250	-0.251	-0.325	0.351	0.434	-0.137	-5.626	-5.254	-1.366
TORSIONAL	27.395	0.998	18.520	13.438	1.140	13.907	10.821	11.178	85.878	78.602	69.674
OUT-OF-PLANE BENDING	6.798	3.538	3.928	3.584	4.071	6.635	3.926	3.942	17.190	15.029	13.620
VAN DER WAALS	151.145	139.289	144.955	146.641	138.699	148.492	145.160	149.934	213.557	195.624	207.493
ELECTROSTATIC	1.741	-0.225	-0.197	-0.195	1.267	0.849	1.348	1.238	9.194	7.769	7.535
TOTAL	313.018	253.512	288.362	277.665	295.342	346.613	319.409	326.269	589.823	539.847	615.649

When referring to structure, this is the view point assignments are made from, on right had side are the Chair (left side up) and Twist boat (Right twist)

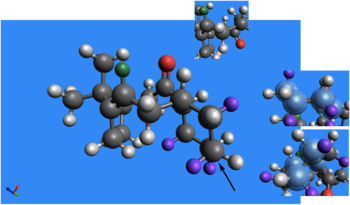
It has been demonstrated by Paquette that in the oxy-Cope rearrangement that leads to this taxol intermediate, there is an atropselectivity in the reaction favoring (relative to the two primary methyls) the alkene hydrogen, carbonyl oxygen and the hydrogens connected to the tertiary carbons that join the six membemred ring to the rest of the structure, to be on the top face of the ring. Over time the structure isomerises to a structure where the oxygen is in the down position.

From the table of calculated energies, we can see that the driving factor for this appears to be the reduction in the angle bending term as we see a 30-50 kJ/mol stabilisation from one structure to the other one of the ways that this is expressed in the structures is with the internal bond angle of the carbonyl changing from 123.4° to 118.3° going from oxygen up to oxygen down, this is a lot closer to the internal bond angle of an unconstrained ketone like acetone which has an internal bond angle of 116.0°

What with the structure having multiple rings there are a number of conformations available for the structure to adopt, the conformation of the large ring can be essentially be expressed by the orientation of the carbonyl.

When looking within the possible conformation of the six membered ring whilst keeping the orientation of the oxygen the same we see that for either orientation of the oxygen, there is one conformation that has a significantly lower energy then the others. OuHu_Chl and OdHu_Chr are both the lowest conformation in their respective oxygen orientations, again if we go to the constituent energies, we see that this seems to be in an effort to reduce the torsional energy in the structure, with the energies of the low energy conformation ~1 kJ/mol compared to ~11-27. As when looking at the conformational energies of cyclohexane, the chair conformation has the lowest energy of the possible conformations in the six membered ring. Also like cyclohexane, there are two forms of the chair, one with the left side up, and the other with the right up. When the oxygen is in the up orientation the chair has the right end down, and when the oxygen changes orientation so does the chair.

There is quite an energy difference when going from Oxygen Up to Oxygen down, however to interconversion from on to the other would require amongst other things the rotation of the C-(C=O)-C bond which would require energy to overcome the constraints imposed by the carbonyl.

as is shown on the table of energies that all all four of the possible are higher in energy than all but one of the conformations where the carbonyl oxygen is on the bottom face. Its appears that a large contribution of this increased energy arises from the 'angle bending energy' term indicating a divergence from the ideal angles of the bonds in the system.

Taxol intermediate dithiol derivative

A derivative of the Taxol intermediate molecule discussed above has been created and described in literature, with ¹³C and ¹H NMR data reported. The compound adds a five membered dithiol ring onto the six membered ring and also replaces an α-carbonyl-hydrogen with a methyl. The molecule will be modeled, the lowest energy conformation structure established with the use of Avogadro then the NMR of the structure is computed. The number of conformations essentially doubles from the previously discussed molecule, because for every conformation that the previous molecule can but at the same time the new ring twists out of plane in one of two directions. While it is not surprising the conformations of the lowest energy structures retain the conformations of the other rings there seems to be little of no change in the energy with the different directions of twisting of the dithiol ring

Energy of Lowest energy Conformations (KJ/mol)

ring twist	Ou_Chl	OdHu_Chr
		MMFF94s	6-31* ΔG
Cw	436.414	420.549	-1651.464
Anti-CW	436.370	420.228	-1651.463

Originally only the the NMR spectra of the anti-CW twists were calculated, as it seemed that these were lower in energy, and while this is the case, assuming the energetic barrier of interconversion is low enough, there will be an equilibrium between the two conformation, and if these have different NMR spectra, so that the experimental NMR spectra might actually have contributions from both of the conformations and indeed perhaps other conformations may contribute to the overall NMR depending on their concentration in the sample. and provided the interconversion activation energy is low enough we can again assume a dynamic equilibrium will arrise. Therefore it should be possible to work out the populations of the different conformations that you might find in the sample.

Oxygen Up structure with Labels

OdHu_Chr1 (http://hdl.handle.net/10042/28268) OdHu_Chr2 (http://hdl.handle.net/10042/28270)

C NMR Oxygen Down OdHu_Chr1m OdHu_Chr2m Shift (ppm) Atoms Shift (ppm) Atoms ref}} 212.229 22 213.0508 22 211.49 148.0756 3 148.0102 3 148.72 120.1392 20 120.2291 20 120.9 94.1116 29 93.2642 29 74.61 60.4256 25 65.9333 25 60.53 54.8848 6 55.02755 6,28 51.3 54.1984 28 55.02755 50.94 49.6903 9 49.6751 9 45.52 49.1394 31 48.1167 31 43.28 46.7723 48 45.7962 48 40.82 41.79555 45,34 44.1553 45 38.73 41.3446 34 36.78 38.7411 18 38.7325 18 35.47 34.1317 21 33.7286 35 30.84 33.6474 35 32.5757 21 30 28.1554 2 28.4152 2 25.56 26.4614 11 26.5147 11 25.35 24.5458 1 24.5797 1 22.21 22.6213 10 24.1734 33 21.39 21.7163 33 22.5872 10 19.83

C NMR with Oxygen Down

Deviation ofC NMR from literature

When comparing the calculated C NMR to the literature NMR values, we see that for the majority of cases there is actually quite a good correlation to experiment. There are a few cases however where there is a small divergence of ~5ppm, initially this was put down to the presence of sulphur in the molecule affecting the calculation, however there are also divergences at carbons far removed from the thiol ring.

When the two NMR calculations are compared to each other it is seen that a minor change in conformation of just the dithiol ring can indeed have a small but significant effect on the calculated spectrum, to the point that the order of chemical shift for some of the carbons change order. Also when looking through the .log file of the calculations the ΔE between the two conformations which was initially shown to be ~300 J, has now dropped to just 1 J furthering the belief that multiple conformations will be present in the NMR sample.

For this reason it is supposed that the reason for this divergence from literature is due to the degree of motion felt about these carbon atoms, as there is a lot of flexibility, even if the molecule isn't completely changing conformation, it is expected that it will still be subject to motions that push it quite far from ground state. When considering the carbons that show divergence they tend to be the same carbons that would experience the greatest amount of motion, either within the possible geometry of a single conformation or carbons that change most from one geometry to another.

Having said this the large divergence of carbon 9 of ~20 ppm could be down to the presence of two sulphurs directly connected to it.

H NMR Oxygen Down OdHu_Chr1m OdHu_Chr2m Shift (ppm) Atoms Shift (ppm) Atoms Ref 5.97 39 6.00 39 5.21 (1H) 3.19 47,50 3.14 49.46 3.00-2.70 (6H) 3.06 49 3.00 50 2.96 46 2.93 47,26 2.82 24 2.81 24,27 2.75 26,4 2.61 4 2.70-2.35 (4H) 2.65 27 2.55 30 2.47 8,40,30 2.48 8 2.33 51 2.34 43,51 2.22 43 2.28 40 2.20-1.70 (6H) 2.00 5,41,19 2.00 5,19 1.84 7 1.85 41,7 1.65 15 1.58 15,23,12,36 1.58 23 1.58 (1H) 1.52 12,36 1.50-1.20 (3H) 1.36 42 1.27 52,37,42 1.31 52 1.20 16 1.22 37,16 1.10 (3H) 0.96 17,14,13 0.95 17,14,13 1.07 (3H) 0.63 53 0.62 53

H NMR with Oxygen Down

Deviation ofC NMR from literature

When looking at the ¹H data, it is quite tricky to compare the calculated values to literature as peaks have been grouped together and they haven't been assigned to specific hydrogen environments. Two values we can directly compare, one being the alkene hydrogen, which is located far from the rest of the peaks,and a hydrogen alpha and anti-periplanar to the carbonyl oxygen. For this second peak we see pretty much perfect agreement, this is likely due to the restriction of motion that the carbonyl group imposes on that part of the molecule. As for the alkene hydrogen, there is a difference ~0.70 ppm, this is quite a significant difference from literature, this could be accounted for by considering the fredom of motion of the CH₂ group attached to it as changes in the adjoined ring have the potential to greatly affect position and alignment of this carbon and hence affect the environment experienced by the alkene environment. As when considering the ¹³C NMR, when the calculated ¹1H NMR values are compered to eachother we see again that a small conformational change like the direction of the dithiol ring twist has a tangible effect on the chemical shifts of the hydrogen environments of the molecule this is most noticeable in the ordering of the peaks, but also noticing that some of the hydrogens change by ~0.20 ppm. It is important to keep in mind when looking at the calculated values that if the calculated shifts lie within 0.05 ppm it will consider them as degenerate, as such the printed value for a grouped set of hydrogens will be an average of that group.

Further Stuff

Energy of Lowest energy Conformations (KJ/mol)

ring twist	Ou_Chl	OdHu_Chr		OdHu_Chr
		MMFF94s	6-31* ΔG	MMFF94s	6-31* ΔG
Cw	436.414	420.549	-1651.464	427.891	-1651.460
Anti-CW	436.370	420.228	-1651.463	428.268	-1651.461

OdHu_TB(http://hdl.handle.net/10042/28266) ODHu_TB2(http://hdl.handle.net/10042/28265)

Continuing on from the possibility of multiple conformations being present, it was decided to run the two ditiol conformations of the next lowest energy structure from the previous section (OdHu_TBr), from the MMFF94s calculations it would appear that, with an energy gap of 2 KJ/mol the concentration of these in solution would be quite low, however after running the 6-31G(d,p) optimisation, the energy difference from the lowest energy conformations is ~-2 J/mol, these structural conformations are lower in energy then the previously calculated, and the variation in energy between all four conformations is <4 J/mol, this would mean that, provided that the energy required to change conformation is low enough, all four of these conformations will be present in large amounts. This realisation calls into question the ability of the MMFF94s method and basis set in being able to compare small variations in energy between different conformations of this molecule. The logical step from here, if time were available, would be to fun all conformations using B3LYP/6-31G(d,p) or higher basis set in such a way as to take account of this relative population in solution.

Crystal structures of catalysts

Crystal structure of Shi catalyst

Bond Lengths of O-C-O moieties

Bond	Length (Å)
O1-C7	1.413
O2-C7	1.441
O2-C2	1.403
O6-C2	1.403
O5-C10	1.409
O4-C10	1.439

We look first at the C2 carbon as they have the shortest bonds, while nothing compared to the C=O bond length, however it is defiantly shorter then a standard C-O bond (~1.43 Å). O(6)-C(2) is thought to be an anomeric interaction, due to the overlap with on of it's lone pairs and the σ^*(O(2)-C(2)) orbital, it also seems align with the π^*(C=O) of the carbonyl. while the LP of O(2) seems to partialy align with theσ ^*(O(6)-C(2)) it seems that there is possibly a direct interaction of a LP on O(2) directly interacting with the π^*(C=O) which explain the degre of bond stabilisation and it is just pure coincidence that the two bonds happen to be the same length.

When looking down the O(4)-C(10) bond we see that neither of the LP are aligned so as to form an anomeric interaction, however a LP of O(5) is able to interact with the σ^*(O(4)-C(10)) orbital however with a dihedral angle of ~140° the effect is slightly reduced, this bond stabilisation causes a destabilisation of the O(4)-C(10) bond, making is slightly longer then the average C-O bond.

Looking lastly at O(1)-C(7) and O(2)-C(7). The LP on bot Oxygens are able to interact woth the other oxygens σ^*(O-C) bond with dihedral angles of 150° and 152° you would expect the anemeric effects (if there is one) to cancel out, however it seems that that 2° difference is enough to tip the balance to stabilising the O(1)-C(7) bond whilst destabilising O(2)-C(7)

Jacobsen Catalyst

Crystal structure of Jacobson catalyst

Crystal structure of Jacobson catalyst

From the crystal structure of the catalyst, we can see that the molecule is dish shaped, the concave face restrict access to the Manganese center meaning that only the convex face can be activated.

We find that the come of the methyl hydrogens on the tertiary-butyl group come into very close proximity makeing some interaction likely.

When synthesising the Salen ligand, to ensure enantiomeric excess of the chosen enantimer, a diamonium cyclohexyl taterate salt is formed, we can see the effect that this has on the strycture by noticing the dihedral angle highlighted in the picture, this causes a twisting of the structure that enevitably leads to selectivity of one structure over another.

Epoxides

Example of Epoxide Optimisation:PG_MSty_Epox2m:(http://hdl.handle.net/10042/28274)

Optical Rotation

Stil_Epox1m_VCD2.png	Stil_Epox2m_VCD2.png
Stil_Epox1m_VCD2.png	Stil_Epox2m_VCD2.png
MSty_Epox1m_ECD2.png	MSty_Epox2m_ECD2.png
Stil_Epox1m_ECD2.png	Stil_Epox2m_ECD2.png

computed properties

Molecule	Stereochemistry	Rotation ( °)	Literature
Methyl Styrene	[1] (S,S)	-45.34	-43.6 deg
	[2] (R,R)	+45.33	45.7
Stilbene	[1] (R,R)	+250.03	+250.08
	[2] (S,S)	-250.02	-249

Example of OR calculation:PG_MSty_Epox1m_OR2(http://hdl.handle.net/10042/28271)

The optical rotation power of a molecule is a measure of the effect that an enantiomericaly pure chiral compound has on plane polarised light. the optical rotation of both enantimers of trans-methylstyrene-oxirane and trans-stilbene-oxirane was calculated using Gaussian. As can be seen from the table, the two enantimers of each compound have essentially equal and opposite magnitude of the angle of optical rotation, and the sign of the rotation for each structure corresponds to literature and they agree on the magnitude. It should be noted that there is quite a bit of variability of literature values of optical rotations, and in most cases it would appear that this is due to measurements on non-enantiomerically pure samples of the molecule.

It was considered that the Optical rotation of the cis arranement of the compunds might need to be done, as it was conseddered a possibility that the alkene could potentially isomerise, during the reaction and thus the cis product could be formed, however it was seen that the barrier to isomerisation is high enough as to be improbable to take place during room temperature reactions

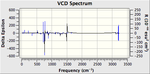
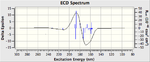
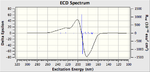
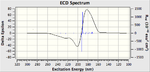
The VCD (Vibrational circular dichroism) and the ECD (Electronic circular dichroism) of all the enantiomers was also calculated and included on the right as additional information, however in depth discussion as it is essentially demonstrating the same thing as the the Optical Rotation calculation, however it does show nicely the equal and opposite effect that the enantiomers have on polarised light.

This data above can be used to assign the enantiomeric assignment of the the products of the reactions with the parent alkene with either Shi or Jacobson catalysts.

NMR

The NMR's of both epoxidas have been calculated using Gaussian, while this can't be used as a means of directly assigning the enantimeric congiguration, but it can be used as a means to corroborate the products of literature and our own experiments. As all atoms are in the 2nd row and above, we expect there to be quite good agreement.

¹H NMR of trans-Methylstyrene oxirane

Structure of Methylstyrene epoxide with atom labels

Msty HNMR

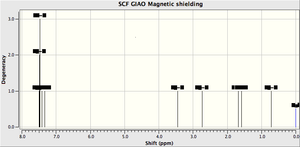
Shift (ppm)	Coupling	Ref	Ref	Atom
7.49		7.36-7.24	7.22-7.36	13,16,14
7.42				15
7.33				17
3.44	(0.8 Hz)	3.57 (2 Hz)	3.50 (2 Hz)	19
2.73	(0.8, 5.2 Hz)	3.04 (2, 5.4 Hz)	3.03 (2, 5.1 Hz)	20
1.32	(5.2 Hz)	1.45 (5.4 Hz)	1.44 (5.1 Hz)	11,12,10

MSty CNMR

Shift (ppm)	Atom	Ref
134.84	5	137.7
123.83	3	128.4
123.15	1	128
122.45	2,6
118.32	4	125.5
61.55	8	59.5
60.11	7	59
18.75	9	17.9

¹H NMR of trans-Stilbene oxirane

Structure of Stilbene epoxide with atom labels

Stilbene HNMR

Shift (ppm)	Ref	Ref	Atom
7.56	7.4-7.3 (10H)	7.4-7.3
7.48
3.53	2.88 (2H)	3.88

Stilbene C NMR

Shift (ppm)	Atom	Ref
133.95	5,9	137.8
123.99	1,16	128.5
123.34	3,18	128.1
122.93	2,17	125.6
122.76	4,19
118.21	6,15
65.76	8,7	62.7

Example of NMR calculation: PG_MSty_Epox2m_NMR (http://hdl.handle.net/10042/28275)

In both cases the Calculated NMRs show good agreement with the literature values for the chemical shifts for trans-methylstyrene and trans-stilbene. There are, as with the NMRs discussed earlier, a few discrepancies due to the limitations of the basis set, the inability to properly model solvent interactions and static model that the NMR spectrum is modeled off of.

The issues with the basis set involve the inaccuracy of 6-31(d,p) to model the diffuse molecular orbitals, this is due to simplifications made to ease computational effort. Provided you keep these limitations in mind, you can still use the results to back up your conclusions. Solvent effects have the potential to play a significant in these sort of calculations, by the very fact that the compund disolves in chloroform indicates that there must be some favorable interaction between the compund and the solvent, these interactions would lead to a lower energy ground state. Not only this but it may also adopt a different form in solutions compared to vacuum in which the calculations take place. Chloroform has the potential to act as a weak hydrogen bond donor possibly explaining why some values are slightly lower than expected

The lack of motion is something mainly directed towards Methyl styrene, the calculations fail to take into account the rotation of the methyl group which will make the three hydrogens merge into one signal, this was displayed in the .log file as three separate peaks at 1.67, 1.59, 0.71 ppm, to get a single value, the shifts from the three protons were averaged to give 1.32 ppm. While this is essentially what is happening in the real world NMR sample, due to this being just a snapshot it is unclear whether this is a true reflection of the distribution of chemical shifts, and as such the average of the three protons. The same issue as above affects the coupling constants as well, we get a J values of 11.6, 2.7 and 1.3 Hz, the same process of just averaging the three numbers gave 5.2 Hz, this is actually surprisingly close to the literature values, this is possibly because H10 is almost completely antiperiplanar to H20 meaning it will be as close to the strongest coupling that it will experience. Still the fact that the rotation of the methyl group is not taken into account seems to be a source of unreliability in the computational method.

Two additional NMRs of methyl styrene have been run to see the effect it might have on the chemical shift of the methyl hydrogens of methylstyrene oxide. In one, the dihedral angle from H10 to the oxygen is set to 180°, and the other where it is at 0°. While the highest of the hydrogens only rises to 1.71 ppm, the average of all six protons (from both calculations) rose to 1.40 ppm. This is a purely empirical experiment to see how the chemical shifts would change, as the structure could not be optimised lest the methyl group rotate back to its previously optimised position. This observation demonstrates that the hydrogen is most deshielded when the dihedral angle is set to 0° so is at its closest point to the oxygen, but also seems to agree with the above commentary.

((after writing the above, it has occured to me that is might be possible to use redundant coordinates to freeze the dihedral angle. Unfortunately it is felt that there is not time enought to run the calculations another time.))

TS Shi

Files used in this and subsequent sections are those provided Computational 1C

Shown in the two tables bellow are the structural free energies for eight of the possible arrangements of the transition state that are possible in the reaction of trans-methylstyrene and the Shi catalyst (a derivative of d-fructose). Four are arranged sich that the product will have (R,R) assignment and the other four will have (S,S), the purpose of this is to determine the structure with the lowest energy and compare it to the lowest energy structure of the opposite enantimer, we can then use this difference in energies to calculate the K value for the competing reactions, from this we can determin a theoretical enantiomeric excess of the preferred enentiomer.

As ever it most be appreciated that the calculations are being done in the gas phase, albeit with a uniform dielectric constant of water. This means that for some of the arrangements, especially with reaction taking place on one face over another, there may be specific solvent effects that mave fovor/disfavor certain arrangements.

MSty R,R

TS		ΔG of TS (KJ/mol)	ΔΔG for (R,R) TS (KJ/mol)	ΔΔG for all TS (KJ/mol)
738037		-3491884.352	0.000	0.000
738036		-3491876.107	8.245	8.245
749615		-3491850.006	34.346	34.346
738028		-3491859.722	24.630	24.630

MSty S,S

TS		ΔG of TS (KJ/mol)	ΔΔG for (R,R) TS (KJ/mol)	ΔΔG for all TS (KJ/mol)
739117		-3491864.329	0.000	20.023
739116		-3491861.792	2.538	22.560
739115		-3491840.568	23.761	43.784
738038		-3491846.649	17.680	37.703

Looking at lowest energy transition structure

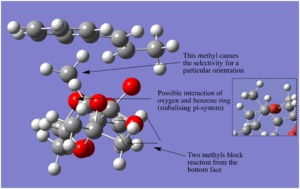
When referring to structural orientations and arrangements it is done so from the structural visualisations depicted for each transition state in the tables.

The entiomeric selectivity of the Shi catalyst is shown quite nicely in the table. We see that for both (S,S) and (R,R) the arrangement with the alkene on the top face of the catalyst with the benzyl ring orientated to the left side if preferred. As shown in the image to the right, there are two methyl groups either side and bellow the dioxygen blocking attack from bellow, and the methyl group sticking up at the back causes unfavorable interactions with the bulky benzyl ring. The favoring of (R,R) over (S,S) is due to the fact that one of the substituents of the alkene is directed towards the methyl sticking up at the back, therefor, in the case of (S,S) where this substituent is a methyl group, this is disfavored. Thus the (R,R) configuration is selected for, further stabilisation of the (R,R) could potentially be due to an interaction of the conjugated π system with the oxygen.

$\mathrm{\Delta }G=-RTln(K)$
$K=e^{\frac{-\mathrm{\Delta }G}{RT}}$
$K=e^{\frac{-20.023}{RT}}$
$K=3.409*10^{-}4$

By using the equation
$ee=\left|\frac{1-K}{1+K}\right|*100$
we can determin a theoretical ee of 99.9% in favor of the (R,R) trans-methylstyrene-oxirane

TS Jac

A similar approach to above was taken for the reaction between trans-methylstyrene. Methylstyrene was chosen because it allows the comparison between the two catalysts.

It should be noticed that the molecule modeled as the catalyst is not the same as that used in experiment Y3S1 or that used in literature, for this reason conclusions based on these calculations are likely to differ quite a bit as the modeled structure is missinf two bulky tert-butyl groups.

caption

	Structure		ΔG (KJmol-1)	ΔG-ΔGmin (KJmol-1)	K
(R,R)	856649		-8796459.922	22.529
	856651		-8796461.294	21.1562	1.97E-04
(S,S)	856650		-8796470.402	12.0484
	999999		-8796482.451	0

$K=e^{\frac{-\mathrm{\Delta }G}{RT}}$
$K=e^{\frac{-22529}{RT}}$
$K=1.129*10^{-}4$

By using the equation
$ee=\left|\frac{1-K}{1+K}\right|*100$
we can determin a theoretical ee of 99.9% in favor of the (R,R) trans-methylstyrene-oxirane

Difference between the lowest energy R,R and lowest energy S,S = 21.1562 KJ/mol
K=e^(-21156/(8.3145*298.15))
K= 1.97E-04
(1-ans)/(1+ans)*100 = 99.98% ee for trans stilbeneoxirane(S,S)

This corrwsponds with the odserved selectivity of Shi however the theorticat ee is much higher than experimental.

A similar critical analysis similar to that done earlier is more difficult to do, as there dosen't seem to be any clear defining structural entity that dictates the selectivity as it did in the case of the Shi catalyst.

Literature was hard to come by in regards to this reaction, however one paper that was found, found that the absolute configuration of the product was (R), however, as no Optical rotation was given in the paper, it is uncertain how this correspons to calculated optical rotations. They did note however that the reactivity of trans-methylstyrene to styrene was 0.39 where as cis-methylstyrene was at 0.75. suggesting that the Jacobsen catalyst is selective for Cis- arrangements over trans-.also suggesting that the enatiomec excess is only as high as 25%. This can most likely be accounted for by solvent effects.

Jac NCI

NCI surfaces of Lowest energy Shi TS

NCI surfaces of Highest energy Shi TS

Shi Transition state

Shown here is the NCI (non-covalent interactions) present in the transition state of the Shi catalyst when reacting with the substrate in its most favorable interaction, a cursory glace was made to compare the topology of the interactions the main interactions are pointed out on the diagram of the NCI. As much as to say that there is a considerable spread of favorable interactiond between the to molecules in the modeled transition state.

QTAIM

QTAIM of Lowest energy Shi TS

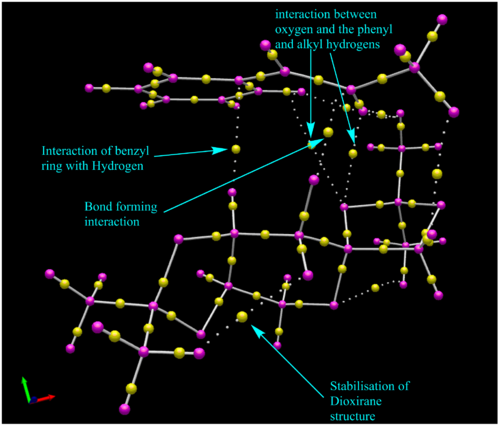
Here we are looking at the bond critical points within the transition state we see that within the C-C bonds in the molecule the sharing of electrons is fairly even, an unusual observation is that the BCP seems to be located closer to the carbon in C-O bons, and closer to the Hydrogen in C-H bonds. It is uncertain what this infers as, if the BCP represents wher the envisioned max electron density would be in a bond, then the points seem to be the wrong way around. perhaps this is due to the fact that electro-negativity isn't taken into account, and is just based on electron densities. That is unless the interpretation of the BCP, if in fact it represents the opposite, such that the BCP is actually the point of lowest electron density then perhaps this would make sense.

The solid lined represent what would be considered covalent bonds, whilst the dotted lines are intermolecular forces, such as Van Der Waals forces or hydrogen bonds. We see that there are multiple interactions between the phenyl hydrogen and alkene hydrogen to the nearby oxygen as well as to the neighboring methyl group. There is also a stabilisation of the dioxirane ring by a nearby hydrogen.

The BCP seem to be located in the same places as the Favorable interactions shown in the NCI above.

Conclusion

It is felt that it has been shown that with the use of computational methods that it is possible to predict, and rationalise the outcome of a reaction. As well as to probe for things that would be impossible any other way, while there are limitations, mainly due to the chosen basis set, we see a wide range of properties and interactions that couldn't be seen otherwise. Such as the NCI and QTAIM calculations that allow us to see the likely intermolecular bonding interactions, both favourable and unfavourable. There is undoubtedly much more that can be done with computational chemistry, and this is something that that we lookforward to exploring in the future.

Look into

Experimental Evidence for Multiple Oxidation Pathways in the (salen)Mn-Catalyzed Epoxidation of Alkenes: DOI:<2568::AID-CHEM2568>3.0.CO;2-Z 10.1002/1521-3765(20020603)8:11<2568::AID-CHEM2568>3.0.CO;2-Z