Rep:Mod:pes116
Inorganic Computational Lab
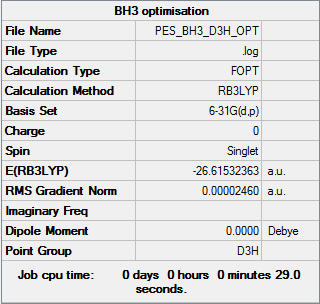
BH3
Calculation method: B3LYP Basis set: 6-31G(d,p)
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000049 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000195 0.001800 YES RMS Displacement 0.000128 0.001200 YES
Log file
Jmol
BH3 |
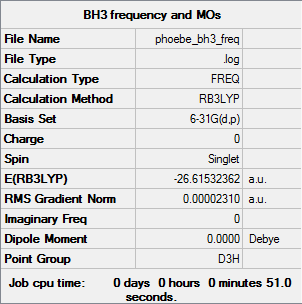
Summary for frequency analysis
Low frequencies table
Low frequencies --- -0.4072 -0.1962 -0.0054 25.2514 27.2430 27.2460 Low frequencies --- 1163.1897 1213.3128 1213.3155
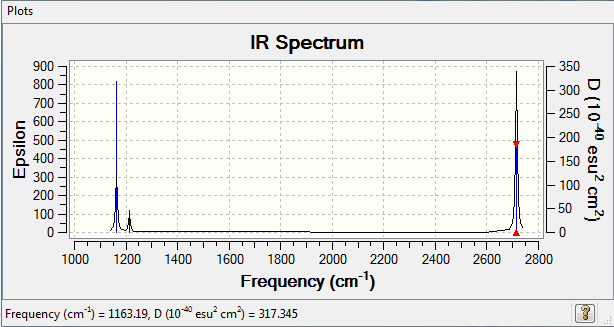
IR spectrum
IR analysis
| Wavenumber (cm-1 | Intensity (arbitrary units) | Symmetry | IR active? | Type |
|---|---|---|---|---|
| 1163 | 93 | A1 | Yes | Out of plane bend |
| 1213 | 14 | E | Very slight | Bend |
| 1213 | 14 | E | Very slight | Bend |
| 2582 | 0 | A1 | No | Symmetric stretch |
| 2715 | 126 | E | Yes | Asymmetric stretch |
| 2715 | 126 | E | Yes | Asymmetric stretch |
Though there are 6 different vibrations shown in this table, these don't all appear in the IR spectrum. This is because some of the vibrations are inactive, because there is no net change in dipole moment during the vibration. As well as this, some of the peaks have such a low intensity that they won't appear on a spectrum.
Smf115 (talk) 16:26, 26 May 2018 (BST)Correct assignment of the vibrational modes however, the symmetries are incorrect. This usually means that your molecule had the wrong point group although both your fequency and optimisation calculations show it to be D3h so the pre-symmetrsation calculation may have been used by accident. Correctly picked up on the IR inactive vibration but to improve, consider the degeneracy of some of the modes too.
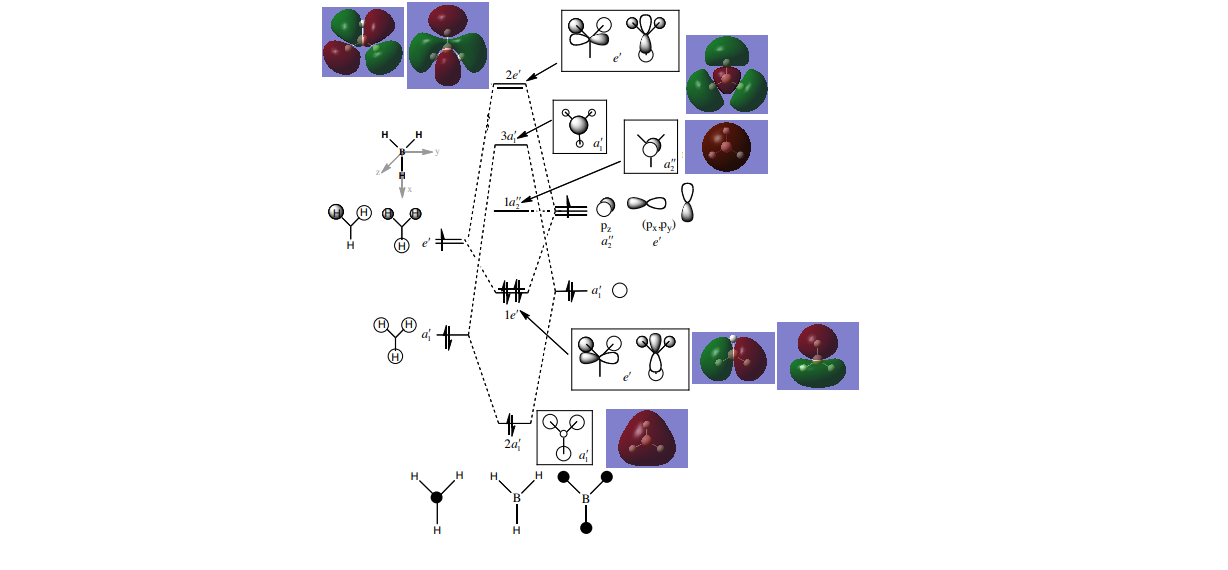
MO diagram
The LCAO diagram for BH3 was taking from the Lecture 4 tutorial sheet at http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf, accessed on 17/05/18.
Comparing the MOs produced by Gaussian to those produced by the LCAO method show that those derived from LCAO do have a small resemblance to those derived by Gaussian as the nodal planes are in the same place. However the MOs produced by LCAO have different shapes, as they don't spread over the whole molecule. Thus LCAO can be used to give a rough prediction of the MOs of a molcule, but the shapes produced by LCAO are not completely accurate.
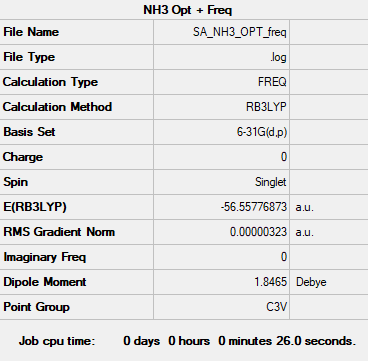
NH3
Calculation method: B3LYP Basis set: 6-31G(d,p)
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Log file
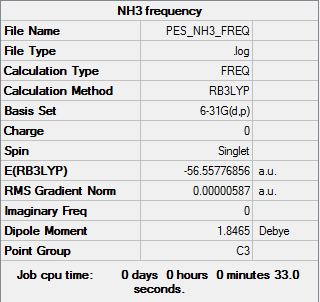
Summary for frequency analysis
Low frequencies table
Low frequencies --- -8.5646 -8.5588 -0.0041 0.0455 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
Jmol
NH3 |
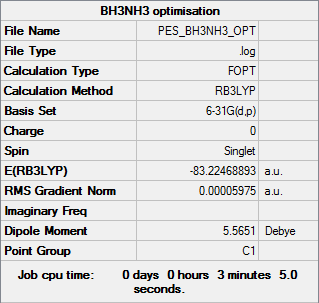
NH3BH3
Calculation method: B3LYP Basis set: 6-31G(d,p)
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000513 0.001800 YES RMS Displacement 0.000296 0.001200 YES
Log file
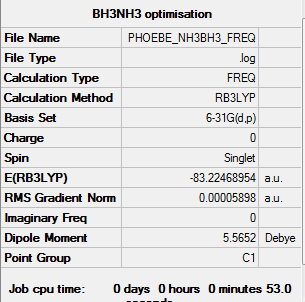
Summary for frequency analysis
Low frequencies table
Low frequencies --- -0.0013 -0.0013 0.0009 14.4660 22.7381 41.6444 Low frequencies --- 266.6526 632.2253 639.1944
Jmol
NH3BH3 |
Association Energy
BH3 Energy = -26.6153
NH3 Energy = -56.5578
NH3BH3 Energy = -83.2246
ΔE = [E(NH3BH3)] - [E(NH3)+E(BH3)] = -0.0515 = -135 kJmol-1
This bond energy is as expected, as a dative bond typically has medium strength. It is weaker than a covalent bond such as C-C at ~350 kJmol-1, but stronger than intermolecular interactions, such as a hydrogen bond at ~20 kJmol-1.
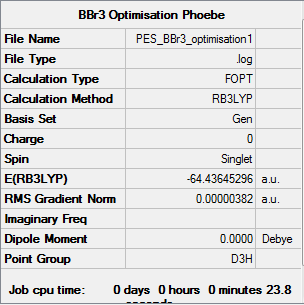
BBr3
Calculation method: B3LYP Basis set: 6-31G(d,p) (B), LANL2DZ (Br)
DSpace Link
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Log file
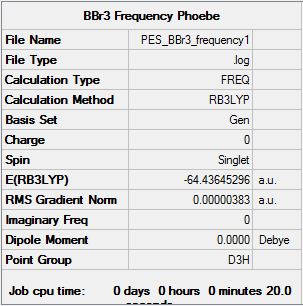
Summary for frequency analysis
Smf115 (talk) 16:25, 26 May 2018 (BST)Good structure information throughout section 1 and it's nice to see both the optimisation and frequency calculation summaries.
Low frequencies table
Low frequencies --- -0.0137 -0.0064 -0.0047 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Jmol
BBr3 |
Aromaticity
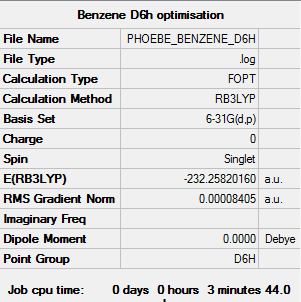
Benzene
Calculation method: B3LYP Basis set: 6-31G(d,p)
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
Log file
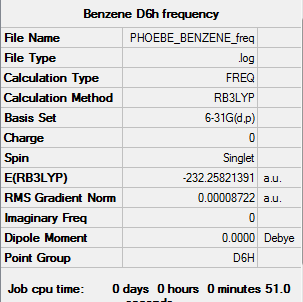
Summary for frequency analysis
Low frequencies table
Low frequencies --- -2.1456 -2.1456 -0.0089 -0.0044 -0.0044 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Jmol
Benzene |
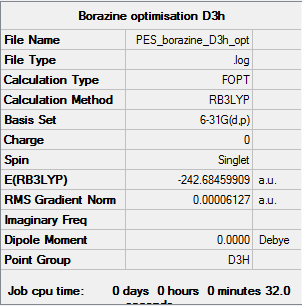
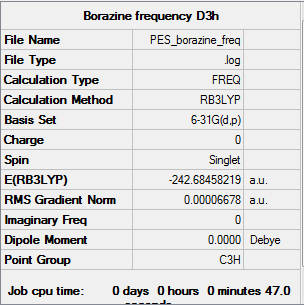
Borazine
Calculation method: B3LYP Basis set: 6-31G(d,p)
Summary table
Item table
Item Value Threshold Converged? Maximum Force 0.000083 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000239 0.001800 YES RMS Displacement 0.000071 0.001200 YES
Log file
Summary for frequency analysis
Low frequencies table
Low frequencies --- -12.7375 -12.7375 -9.0340 -0.0211 -0.0104 -0.0104 Low frequencies --- 289.1108 289.1108 403.8400
Jmol
Borazine |
Charge distribution
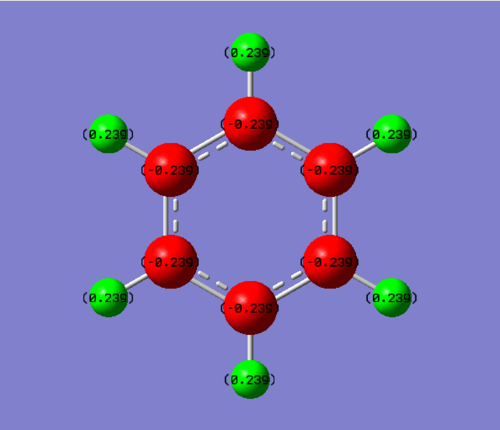
In benzene, all the carbon atoms have a charge of -0.239 Db whilst each hydrogen atom have a charge of +0.239 Db. Carbon is slightly more electronegative than hydrogen, which explains why the carbon atoms have a slight negative charge and the hydrogens have a slight positive charge. As benzene has a centre of inversion, it has no net dipole. As well as this, the charges cancel out, so the benzene molecules is neutral.
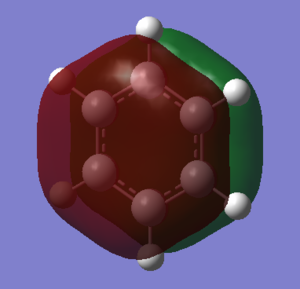
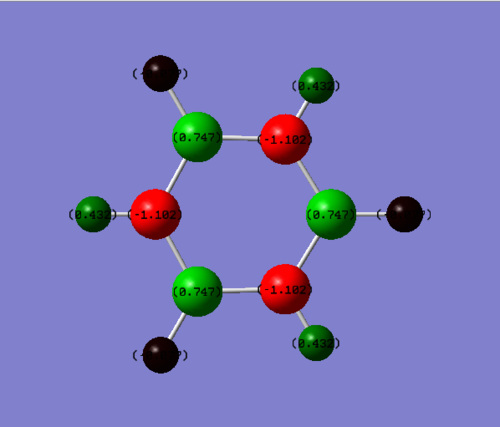
In borazine, the boron atoms are positive, with a charge of +0.747 Db, whereas the nitrogen atoms are negative, with a charge of -1.102 Db. This is because nitrogen is more electronegative than boron. The hydrogen atoms which are bonded to boron have a slight negative charge of -0.077 Db, as boron is more electropositive than hydrogen. However the hydrogen atoms which are bonded to nitrogen have a positive charge of +0.432 Db, as nitrogen is a lot more electronegative than hydrogen. Over the whole molecule, the charges cancel, leaving a neutral molecule. There is a slight net dipole in borazine, because of its reduced symmetry. In the molecule, a N-B-N unit is opposite a B-N-B unit, so the differences in charges in these units leaves a net dipole on the molecule.
Smf115 (talk) 22:49, 26 May 2018 (BST)Good justification of the charge distribution arising from the electronegativities and mention of the neutraility and dipoles of the molecules. However, the same colour range should have been used across both molecules to highlight the charge distribution.
MO comparison
| Benzene MO | Borazine MO | Discussion |
|---|---|---|
 |
 |
These diagrams show benzene MO 13 and borazine MO 16, which are occupied sigma orbitals that have antibonding character. There are 3 nodal planes running across the molecule, but in borazine there are also nodal planes on each of the boron atoms, resulting in more antibonding character and a higher energy. |
 |
 |
Benzene MO 17 and borazine MO 17 are occupied pi bonding orbitals. They are delocalised orbitals with one nodal plane, which sits in the plane of the molecule. The two MOs are very similar in both molecules, as the symmetry doesn't change much in borazine. This means the two MOs are reasonably similar in energy. |
 |
 |
The 19th MOs of benzene and borazine are occupied sigma character MOs. In each of them there are 4 nodal planes across the molecule and they both have strong antibonding character. The borazine MO has lower symmetry than the benzene MO, resulting in a higher energy. |
Aromaticity discussion
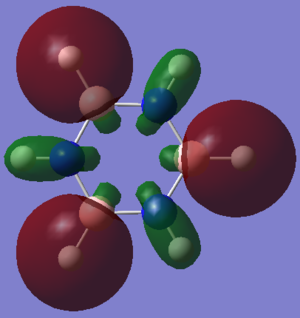
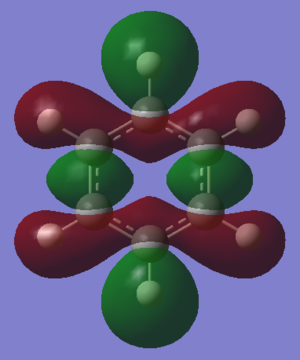
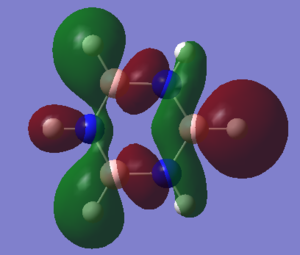
The basic explanation of aromaticity suggests that the overlap of p-orbitals leads to the formation of pi molecular orbitals in which the electrons are delocalised. The delocalisation of the system results in a stable aromatic molecule. The MO 17 of benzene and borazine show a molecular orbital which fits the basic description of aromaticity. In the orbitals, there is an area of electron density above and below the plane of the ring, covering the whole ring, with a nodal plane along the plane of the molecule. This is formed through the overlap of the p-orbitals which are orthogonal to the plane of the ring.
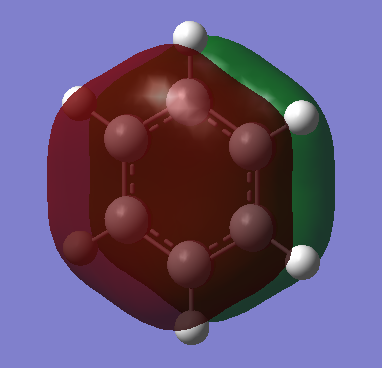
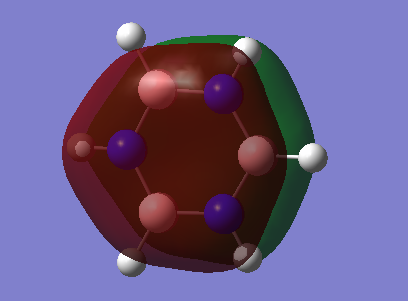
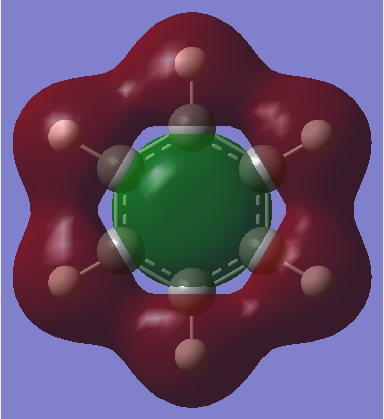
However, the p-orbital overlap is not sufficient to describe aromaticity, as the sigma framework has a large contribution to aromaticity.[1] It is suggested in literature, that in the case of benzene, the pi electrons prefer to localise, whilst the sigma electrons prefer to delocalise.[2] There is much more sigma delocalisation in benzene, such as in MO 12, than in borazine (MO9), which explains why the energy of benzene is lower than that of borazine, as it gains more stabilisation from delocalisation.
 |
 |
|---|
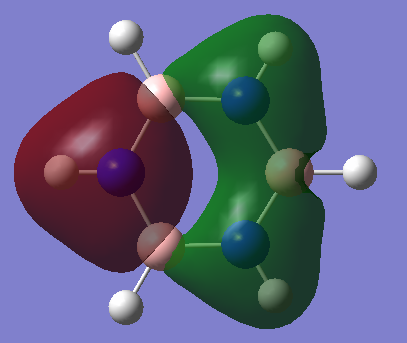Smf115 (talk) 22:44, 26 May 2018 (BST)Great reference to the MOs visualised in benzene to explain why overlapping pZ AOs is a bad descriptor of aromaticity. To improve, the key concepts and definitions of aromaticity should have been discussed such as Huckel's rule and why some of these concepts no longer hold.
Smf115 (talk) 22:44, 26 May 2018 (BST)Overall a well presented report with clear answers and good structure information throughout.