Rep:Mod:parkbom
Module 3 - The Computation of the Transition State
Introduction
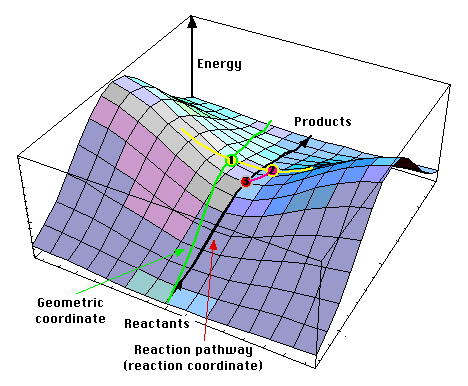
The Transition State is an energetic maximum within a given reaction coordinate and represents the point at which bond breaking and bond forming is occurring simultaneously. This is represented by dotted lines in formal notation and depicts the transient nature of the bond(s) in question in the transition state.
The analysis of potential energy surfaces are effective in finding transition states; the transition states can be described graphically as "dams" that represent energy metastability, that the reactants must "cross" in order to form the products.
| Potential Energy Surface Reaction Coordinate[1] | Cope Rearrangement[2] |
 |
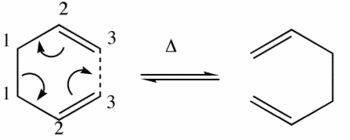
|
From the point of view of computational chemistry, the methods of molecular mechanical structure determination that employed imaginary force fields are ineffective in the calculations concerning the transition state in larger molecules, as they do not define the dynamics of bond making and bond forming that are apparent in the transient nature of the transition state.
As such, in combination with molecular orbital based calculations, the following of the potential energy surface of a molecule can be used to locate and analyse the transition state.
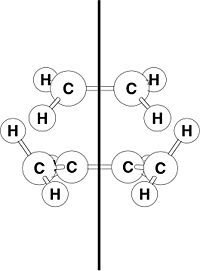
This computational exercise concerns the rearrangement of 1,5-Hexadiene in the Cope Rearrangment(above).
The Cope Rearrangement proceeds via a [3,3]-Sigmatropic shift involving the motion of 6 electrons and is thermally-driven.
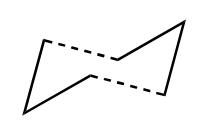
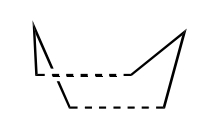
In terms of transition states, the cope rearrangement can reportedly proceed via two checkpoints, the boat or the chair:-
| Chair | Boat |
 |
|
The purpose of this exercise is to ascertain which reaction pathway is preferred by computation of each transition state in the elucidation of geometry, repective energies and other thermochemical data.
Exercise 1 - Optimising the Reactants and Products
In this section, the "reactant" 1,5-hexadiene and the "product" 1,5-hexadiene are modelled in correspondence to the cope rearrangement.
The flexible nature of 1,5-hexadiene means that there is an initial dilemma of likely conformation at rest.
Several starting conformations were thus taken and their geometries optimised to find the lowest energy conformer.
Initially, 1,5-hexadiene was taken, ensuring a roughly "anti" linkage in the centre of the molecule, so that the central C atoms 3 and 4 are approximately antiperiplanar to one another. This molecule was cleaned in the gaussview builder interface and then taken and optimised using the Hartree-Fock method with basis set 3-21G through Gaussian.
b) similarly, a synclinal, or "gauche" version of 1,5-hexadiene was taken and optimised at the HF 3-21G level.
The energies of both conformers and also their symmetry were noted.
| "Anti" 1,5-Hexadiene | "Gauche" 1,5-Hexadiene |
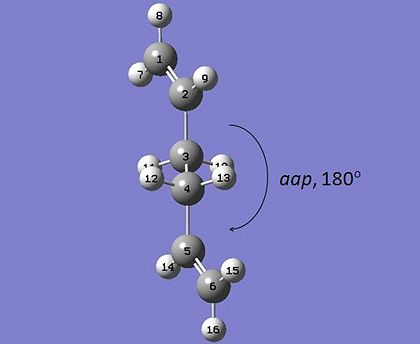 |
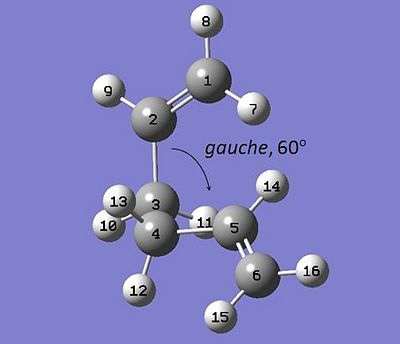
|
| Confomer | Anti-1,5-Hexadiene | Gauche-1,5-Hexadiene |
| Total Energy(a.u.) | -231.69254 | -231.69266 |
| Point Group | ci | None |
From a purely steric-orientated argument, the anti configuration should have a lower energy than the gauche, as there is less steric hindrance from the two ends of the carbon chain 180 degrees from one another than next to each other in the gauche conformation.
As it so happens, the energy for the anti conformer is reportedly lower than that of the gauche conformer, but by a minute amount of roughly a ten-thousandth of a hartree (1 hartree = 4.3597482E-18 J).
Even so, it was appreciated that the central C-C-C-C linkage of 1,5-hexadiene lends itself to quite a high degree of rotational freedom, and thus, further examples of conformational isomerism. This is reinforced by the fact of the two remarkably different conformers having remarkably similar energies, and points to the fact that 1,5-hexadiene experiences conformational ambiguity often[3].
As such, 2 other conformers were taken and optimised:-
| Different Conformers of 1,5-Hexadiene | |||||||||||||||
| (g120,a,g120)-Anti1 | (g120,a,g-120)-Anti2 | (g120,g-60,g120)-Gauche1 | (g120,g60,g-120)-Gauche3 | ||||||||||||
|
|
|
| ||||||||||||
| Energy(a.u.) | |||||||||||||||
| -231.69260213 | -231.69253506 | -231.69166702 | -231.69266120 | ||||||||||||
| Point Group | |||||||||||||||
| C2 | Ci | C2 | C1 | ||||||||||||
The energies here from the HF 3-21G are similarly close, but contrary to what was expected, it was found that gauche3 was actually the lowest in energy.
Beneath this, the anti conformers are found to be lower in energy than the other gauche conformer. This may be rationalised as the minimalisation of steric hindrance lowering the energy of the overall molecule, as the antiperiplanar groups maintain the least steric strain.
However, the cis-gauche conformer is lowest in energy due to stereoelectronic arguments.
The π-bonds of the C=C bonds are lying criss-crossed over each other in this conformer. This promotes effectual π-molecular orbital overlap and hence stabilises the molecule.
Next, the anti2 conformer with ci symmetry and the gauche1 conformer was taken and further optimised under the DFT B3LYP method with a more sophisticated basis set, 6-31G(d).
The resulting optimised molecule was then compared with the earlier attempt in terms of energy.
A further frequency analysis was conducted in order to check that the optimisation has proceeded to a minimum, being the case when all frequencies were real and positive.
| Comparison of the HF 3-21G and DFT B3LYP 6-31G(d) Optimisations | ||||
| Method | HF 3-21G | DFT B3LYP 6-31G(d) | ||
| Conformer | anti2 | gauche1 | anti2 | gauche1 |
| Total Energy(a.u.) | -231.69253506 | -231.69166702 | -231.61170616 | -231.61068821 |
| 1-2 C=C Bond Length (A) | 1.3162 | 1.3156 | 1.3335 | 1.3331 |
| 2-3 C-C Bond Length (A) | 1.5091 | 1.5041 | 1.5083 | 1.5044 |
| 3-4 C-C Bond Length (A) | 1.5527 | 1.5481 | 1.5508 | 1.5482 |
| 4-5 C-C Bond Length (A) | 1.5091 | 1.5041 | 1.5083 | 1.5044 |
| 5-6 C=C Bond Length (A) | 1.3163 | 1.3335 | 1.3157 | 1.3331 |
| 1-2-3-4 Dihedral (o) | 114.66 | 118.49 | 123.93 | 124.24 |
| 2-3-4-5 Dihedral (o) | 180.00 | 180.00 | -64.18 | -65.01 |
| 3-4-5-6 Dihedral (o) | -114.66 | -118.49 | 123.93 | 124.24 |
As can be seen here, the energies returned differ in a noticeable manner. However, comparison of energies computed under different basis sets is unbalanced.
As such, comparisons of the geometry are notably more reliable in discerning the computed differences.
The bond lengths differ by negligible amounts. However, it can be seen that the various dihedral angles have been "tightened" more to their ideal figures (closer to 120o for the anticlinal dihedrals.
As such, using a more sophisticated basis set ensures a more accurate approximation to reality.
The log file yielded the following thermochemical data:-
1)Sum of electronic and zero-point Energies= -234.469195
2)Sum of electronic and thermal Energies= -234.461847
3)Sum of electronic and thermal Enthalpies= -234.460903
4)Sum of electronic and thermal Free Energies= -234.500782
Theses values concern the 1)Potential Energy at 0K that includes the zero-point vibrational energy term 2)Potential Energy at 298.15K and 1atm and adds contributions from translational, rotational and vibrational energy 3)Energy including a correction for RT(H=E+RT) for dissociation reactions and 4)The Entropic contribution.
Exercise 2 - Optimising the "Chair" and "Boat" Transition Structures
The Cope Rearrangement has been found to proceed via one of two possible transition states with differing conformation, as mentioned in the introduction:-
| Cope Rearrangement Transition State Conformations | |
| Chair | Boat |
 |

|
When the rearrangment is thought as one that is concerted and proceeds with synchronicity of bond breaking and formation, these two transition states come to mind.
There is indeed a third type of transition state for this reaction, dubbed the Dewar transition state, that reportedly proceeds via a diradical tight-chair intermediate species that was discovered by Dupuis et al.[4], and is thus NOT concerted.
The Chair Transition State
The chair transition state was initally synthesised using two "resonant" allyl (C3H5) fragments in gaussview, which were optimised under the 3-21G basis set, and subsequently placed in appropriate positions relative to one another to be optimised into the transition state.
| Allyl Fragment(C3H5) | |
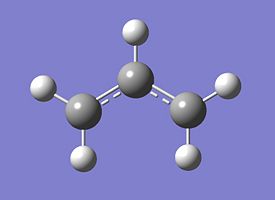
| |
| sp3 Centre Bond Angle (o) | 109.5 |
| Allyl C-C Bond Angle (o) | 124.3 |
| C-C Bond Length (A) | 1.54 |
| C=C Bond Length (A) | 1.34 |
| Allyl C-C Bond Length (A) | 1.39 |
The optimised allyl C-C bond angle is greater than the normal sp3 bond angle of 109.5o due to resonance.
More importantly, the allyl C-C bond length is between that of a single bond and a double bond.
This optimised allyl fragment was then taken, duplicated and placed, facing opposite directions, with roughly a 2.2A distance between the terminal carbons of each fragment to mimic the shape of the chair transition state.
Thus, a frequency + optimisation was run that directed gaussian to reach a TS(Berny), with the elucidation of force constants.
The optimisation was then repeated but this time using the "frozen" coordinate method, effectively fixing the two pairs of ends at a distance of 2.2A.
Clearly, this method requires that the general structure of the transition state in question be known. However, by fixing the positions in such a way, a more accurate optimisation can be done that avoids divergence.
Finally, the optimisation was performed a third time, using a normal guess Hessian method, which involves calculation of the force constant matrix.
After the three optimisations were complete, the following data were obtained:-
| Optimisation of Chair Transition State | |||||||||||
| Structure | |||||||||||
| TS(Berny) | Frozen Coordinate | Hessian | |||||||||
|
|
| |||||||||
| Energies (a.u.) | |||||||||||
| -231.61932 | -231.61932 | -231.69167 | |||||||||
The structures returned from the normal force-constant calculation optimisation and the frozen coordinate method are indistinguishable from first glance, and their energies are virtually identical. However, the structure obtained from the Hessian is different, and so is its energy value.
FREQUENCY ANALYSIS
Vibration-wise, there was one negative, and thus "imaginary" frequency found with a wavenumber of -817.91cm-1.
When the stretch was visualised, the following was observed:-
| Imaginary Stretch at -817.91cm-1 |
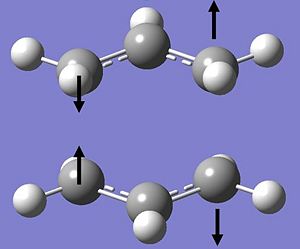
|
The appearance of this imaginary frequency resembles the motion that would ensue under the Cope Rearrangment - the action of bond breaking of the C-C σ bond in the middle of the 1,5-hexadiene with the subsequent formation of a new σ bond on across the terminals on the other side.
The fact that there is only one imaginary frequency value points to the notion that the cope rearrangment through this transition state is concerted, and thus occurs in one synchronous step.
The number of imaginary frequencies produced from a frequency analysis for the midpoint of a reaction points towards the synchronicity of the reaction[5].
The Boat Transition State
For the boat transition state, a different method was utilised, namely the QST2 method, whereby reactant and product are defined, and the transition state is converged from these.
This required the previously optimised 1,5-hexadiene molecule to be taken and numbered along its carbon skeleton.
The molecule was then duplicated and juxtaposed to the intial "reactant" molecule and renumbered in such a way to reflect the reacted, rearragement "product" as shown below:-
|
The first instance of optimisation failed to produce an output, and thus the molecule was changed in the following way:-
The dihedral angle of both reactant and product were changed to 0 degrees, such that the two carbon groups either side of C3 and C4 are eclipsed, and the C2-C3-C4 and C3-C4-C5 bond angles were both changed to 100 degrees.
The modified structures were once again optimised under the QST2 method to yield the following structure:-
| QST2 Optimised Boat Transition State |
|
DISCUSSION
Here, it is illustrated that the QST2 method is automated, and is thus very efficient, but is only effective if the shape provided of the reactants and products cloely mirror that of the transition state, otherwise convergence is difficult.
The QST3 method was also attempted [6], whereby an addition guess of the transition state geometry was implemented. If the guess of the transition state is sound, then the QST3 is by far more accurate than the QST2 method, and does not rely so much on the shape of the reactants and products.
initally, it would seem that in order for the cope rearrangement to occur, to two carbon terminals would be required to be close to one another. This is not the case with the "anti" conformers of the molecule, as the terminals are situated as far apart as they may possibly be, antiperplanar to one another.
Once free rotation moves the carbon groups closer together, into the gauche configuration, where the terminals are more poised to react, cope rearrangement would proceed.
The relative orientations of the vinyl groups would ultimately dictate which transition state would be traversed. For instance, if the vectors of the vinyl groups cross, such as the case for the gauche1 conformer, then as the terminals align into a bonding orientaton, the chair conformation would be adopted by the transition state.
Conversely, if the two vinyl groups lie in a pseudo-parallel fashion, where their vectors do NOT cross, such as is the case for gauche3, then the transition state would be of boat topography.
IRC
The Intrinsic Reaction Coordinate looks more cloesly at the potential surface of a reaction and works to pinpoint the highest point in a local area of the potential surface by creeping up the steepest slopes in the immediate area.
This calculation was attempted with 50 points, and did not converge within the maximum number of points.
Thus, this was carried out again whilst calculating the force constant every single point.
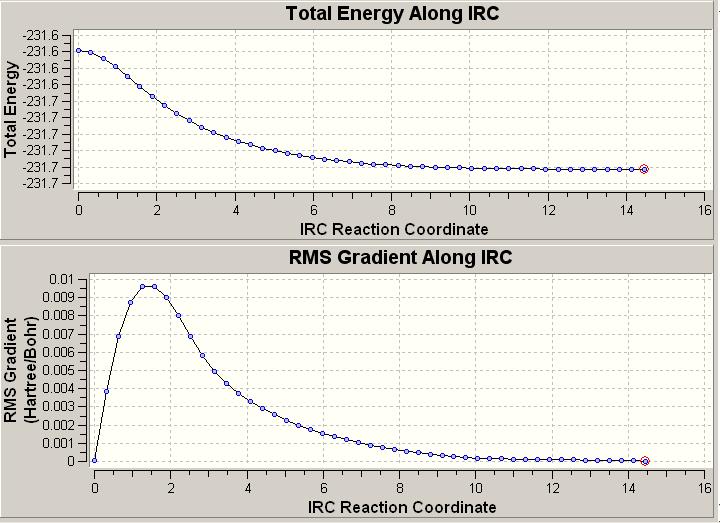
|
Here, upon closer inspection of the RMS Gradient of the energy, the gradient falls to zero, thus indicating that a minimum has been reached.
Energy Calculation
The two transition states were optimised a final time under DFT B3LYP 6-31G(d) conditions.
The geometries that were outputted were very similar to the previous examples, however, the energies received for both transition states are notably more varied:-
Final Energy of Chair Conformation (a.u.) = -234.61071 Final Energy of Boat Conformation (a.u.) = -234.54309
Here, it can be conclusively said that the Boat conformation transition state is indeed lower in energy than the Chair conformation.
This corresponds to better orbital overlap of the adjacent carbons on the framework, which are exactly eclipsed and not staggered like in the chair formation.
The Diels-Alder Cycloaddition
| Diels-Alder Reaction of Butadiene and Ethylene |
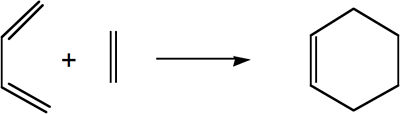
|
The Diels-Alder Reaction is an example of a pericyclic cycloaddition, that usually involves the reaction between an electron rich diene and an electron poor dienophile.
The process is described as a [4s + 2s], 6 electron process that forms 2 new σ bonds.
When viewing the molecular orbital picture of butadiene and ethylene, the molecular orbitals are classified as either s(symmetric) or a(antisymmetric) in relation to the bisecting plane as shown below.
| Bisecting Plane for Diels-alder |
|
Investigation of Molecular Orbital Symmetries of Butadiene and Ethene
Butadiene and Ethylene were optimised and their molecular orbitals visualised:-
Butadiene
The HOMO and LUMO are considered with reference to the bisecting plane to determine their symmetry:-
| HOMO and LUMO of Butadiene | |||
| Molecular Orbital | 2D Representation | 3D Representation | s/a |
| HOMO | 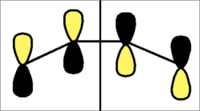 |
 |
a |
| LUMO | 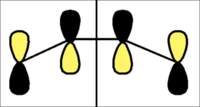 |
 |
s |
Ethene
Similarly, the HOMO and LUMO of ethylene were characterised:-
| HOMO and LUMO of Ethene | |||
| Molecular Orbital | 2D Representation | 3D Representation | s/a |
| HOMO | 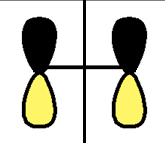 |
 |
s |
| LUMO | 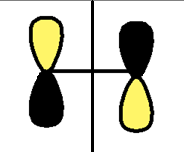 |
 |
a |
Optimisation of Diels-Alder Transition State
The Transition State whereby the concerted cycloaddition of butadiene and ethylene was modelled to a guess initially, before being optimised under HF 3-21G basis set conditions to a TS(Berny).
The initial guess was modelled from the bicyclo-system of cyclohexene and subsequently removing one of the -CH2CH2- arches to arrive at an "envelope"-shaped 6-membered ring.
The new σ bonds were stripped before the optimisation.
A frequency analysis was first concocted via optimisation to a transition state.
There were 3 imaginary frequencies reported by the analysis, detailed below:-
| Imaginary Frequency Vibrations of Transition State | |||
| Stretches | 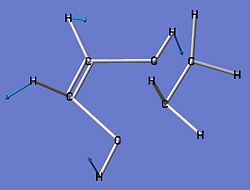 |
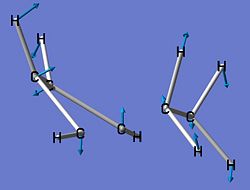 |
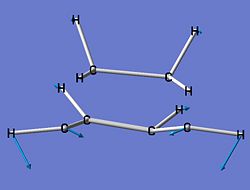
|
| Frequency (cm-1) | -716.19 | -557.32 | -198.58 |
The first imaginary frequency at -716.19cm-1 did not correspond to any particular action within the transition state.
However, it can be seen that the 2nd and 3rd vibrations tie into the formation of the two conformations of cyclohexene, i.e. the chair and the boat.
The presence of 3 imaginary frequencies in the analysis points to the notion that the formation of the two bonds is asynchronous.
The average of the inter-C-terminal distances was then calculated and used in a separate frozen-coordinate optimisation to a minimum, to get a more accurate representation of the geometry:-
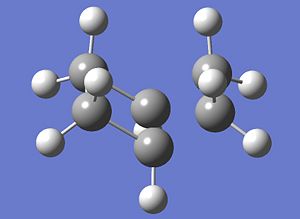
| Comparisons of the Optimisations of transition state | ||
| Method | Ts(Berny) | Frozen-Coordinate |
| Structure |  |
|
| Energy(a.u.) | -230.30655 | -231.67157 |
The length of the partly formed σ C-C bonds were optimised to a value of 1.5075A, which is notably in between the lengths of sp2 and sp3 bond lengths of 1.34A and 1.54A and is a result of the point of breaking of the double bonds in the diene and formation of new σ bonds between the butadiene and ethene.
The Van-der-Waals radius of carbon is 1.70A.
By freezing the terminals, the energy of the optimised structure is markedly higher.
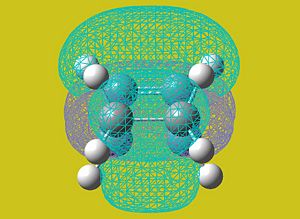
AM1 Molecular Orbital Analysis
The AM1 semi-empirical method was used to visualise the highest-occupied molecular orbital of the transition state.
| HOMO | LUMO |
 |
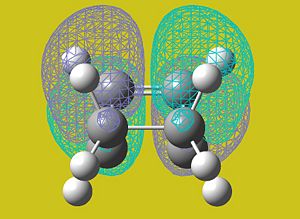
|
| Symmetry | |
| s | a |
With reference to the bisecting plane as shown above, the HOMO of the transition state can be seen to be symmetric when reflected.
The individual MOs of butadiene and ethene thus must both be symmetric with respect to the plane in order to react in such a fashion.
This is consistent with the idea that only molecular orbitals with the same symmetry are allowed to react.
Given this, the pertinent orbitals that are symmetric are the LUMO of the butadiene and the HOMO of the ethene.
As such, electron density is donated into the empty π* LUMO of the butadiene.
The LUMO in this case is antisymmetric with respect to the bisecting plane and corresponds to the HOMO of the butadiene and the LUMO of the ethene.
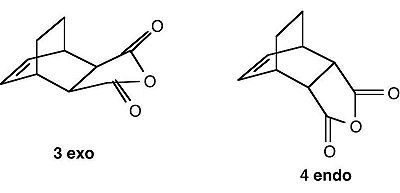
Diels-Alder Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride
The Diels-Alder reaction of Cyclohexa-1,3-diene and Maleic Anhydride is also an example of a 6-electron [4+2] Diels-Alder Cycloaddition intrinsically.
However, it differs from the reaction between butadiene and ethene in that there is now a question of regioselectivity; the bigger anhydride ring can either react to adopt an EXO or an ENDO topography:-
|
The vinyl goup on maleic anhydride, in comparison to ethene, is electron-deficient, thanks to the highly electron-withdrawing nature of the anhydride group.
References
- ↑ http://www.ch.ic.ac.uk/motm/porphyrins/TSdiscovery.html
- ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/
- ↑ Cope Rearrangement of 1,5-Hexadiene: Full Geometry Optimizations Using Analytic MR-CISD and MR-AQCC Gradient Methods, doi:10.1021/jp0259014
- ↑ The Cope Rearrangement Revisited, DOI:10.1021/ja00026a007
- ↑ Cope Rearrangement Revisited, DOI:10.1021/ja00026a007
- ↑ QST Calculation, http://hdl.handle.net/10042/to-2902
