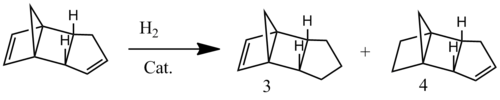Rep:Mod:osef-module1

Module 1 - Organic Pierre Boufflet

Basics of Molecular Mechanics

Predicting geometries and hence regioselectivity of reactions using molecular mechanics

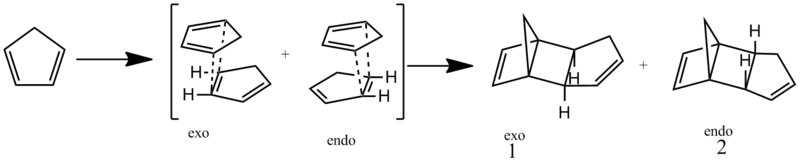
Hydrogenation of cyclopentadiene dimers

Endo vs. Exo

Cyclopentadiene readily dimerises in a Diels-Alder reaction (i.e. [4+2]-cycloaddition). Such concerted reactions proceed via a cyclic transition state, thus defining the stereochemistry quite early in the reaction coordinate. Energies of the cyclopentadiene dimers were calculated using MM2 force field in ChemBio3D Ultra. From this it is predicted that the endo dimer 2 has a higher energy than the exo dimer 1, with energies being 34.014 and 31.880 kcal/mol respectively. Hence the exo product should be the major product experimentally, under conditions of thermodynamic control. In fact, the endo dimer 2 is formed selectively (kinetic control), unless significant heating is applied to allow reversibility and hence provide more thermodynamic control.

Regioselectivity of hydrogenation

Hydrogenation of the endo dimer 2 gives the tetrahydro-derivative. However, partial hydrogenation leads to the dihydro-derivative, which can exist as 2 regioisomers, dimers 3 and 4. MM2 calculations of these two dimers indicates that dimer 3 has a total energy of 35.287 kcal/mol, compared to 31.174 kcal/mol of the dimer 4. From Hammond's postulate, it can be predicted that the transition state of dimer 4 has a lower energy than that of dimer 3, since the corresponding product is lower in energy. Therefore, under both thermodynamic and kinetic control, dimer 4 should be formed preferentially. This can be rationalised by the fact that the unsaturation which is hydrogenated from going from 2 to 4 is more reactive, due to the increased strain induced by the bridging methylene group. Consequently, this bond is hydrogenated at a faster rate.

Clockwise from top left: dimer 1 (exo), dimer 2 (endo), hydrogenated dimer 3 (endo), hydrogenated dimer 4 (endo)

Contributions to the total energy

Energy (kcal/mol)	Dimer 1	Dimer 2	Dimer 3	Dimer 4
Stretching	1.281	1.255	1.113	1.098
Bending	20.57	20.826	12.986	14.542
Torsion	7.667	9.512	16.899	12.512
Van der Waals	4.236	4.308	6.08	4.504
Non-1,4 Van der Waals	-1.415	-1.499	-1.314	-1.079
Total	32.339	34.402	35.764	31.577

Note: Van der Waals appears as 1,4 VdW ChemBio3D. Dipole-dipole and stretch-bend energies are omitted.

In the pair of dimers 1 and 2, the main difference in energies arises due to a considerable difference in torsion. Dimer 2 contains approximately 2 kcal/mol more torsion energy. This can be rationalised by the fact that in dimer 2, there is a hydrogen from the cyclopentene unit which points towards the 5-membered ring on the opposite face. In dimer 1, torsional strain arises from the hydrogens on the methylene bridge pointing towards the endo orientated cyclopentene unit.

Stereochemistry of nucleophilic additions to a pyridinum ring (NAD⁺ analogue)

Higher Energy reactant 5 (Top), Lower energy reactant 5 (Bottom)

Reactant 7 (Note: downwards facing C=O)

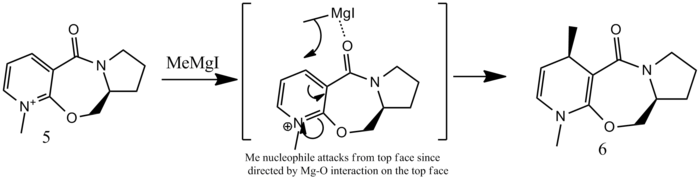
Reactant 5: Regio and Stereochemistry

Reactant 5 can be optimised using MMFF94 force field, to give an energy 57.53 kcal/mol and 59.02, depending on the conformation of the tetrahydropyrrole ring. However, if one attempts to optimise reactant 5 and MeMgI with MMFF94, the optimisation fails because the force field does not contain data for Mg atoms. The particular stereoselectivity of the reaction (addition of methyl group on the top face of the pyridinium ring) is due to the mechanism of the reaction. The Grignard reagent approaches the carbonyl group, the Mg centre coordinates to the O atom, and the para- position of the pyridinium is attacked due to a build up of positive charge at that particular position. The free ortho- position could also be attacked by the carbon based nucleophile, but is hidered by the methyl group on the nitrogen, and does not benefit from the interaction with the carbonyl. The Mg atom of the Grignard reagent preferetially chelates to the carbonyl oxygen, hence rendering the approach of the methyl group at the para- position easier. Since the carbonyl is facing above the plane of the rings, the methyl group consequently approaches and adds from the top face, resulting in the observed stereochemistry.

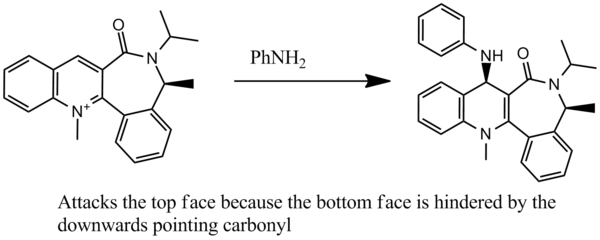
Reactant 7: Stereochemistry

Reactant 7 can be optimised to 99.73 kcal/mol. No other low energy conformers containing an upward-pointing methyl substituent on the cycloheptane ring could be found. The stereoselectivity of the reaction of 7 with benzylamine can be explained, again, by the position of the carbonyl oxygen. This time, it is located below the plane of the ring. The para- position is the only accessible position on the pyridinium ring, so regioselectivity of the reaction is not an issue. Due to the downward-facing nature of the lactam carbonyl, the benzylamine approaches from the less hindered top face. This differs from the previous example where the chelating nature of the Grignard reagent dictated a same-face attack. Experimental observations confirm this prediction, and the product exhibits additional stabilisation due to interactions between the benzylic protons and the methyl group located above the lactam ring.

Stereochemistry and reactivity of an intermediate in the synthesis of Taxol

Conformations

A tricyclic intermediate in the synthesis of Taxol contains two main features which influence the preferential conformation. The first of these is the cyclohexane ring, which can exist either as the twist boat or the chair. An unsubstituted cyclohexane ring usually adopts the chair conformation, which from MM2 calculations is lower in energy by approximately 5.4 kcal/mol (11.92 vs. 6.56 kcal/mol). Particular attention must be paid to the stereochemistry of the hydrogens situated at the ring junctions when going from the twist boat to the chair conformation. The carbonyl group, can point up (intermediate 9) or down (intermediate 10). Therefore, there are 4 major conformations for the intermediate: 9 (chair), 9 (boat), 10 (chair), and 10 (boat). Their structures and energies are shown in the table below (click on the buttons to show the Jmol 3D structure).

Structures and energies of intermediate

	Taxol intermediate (up)	Taxol intermediate (down)	Taxol intermediate (up, chair)	Taxol intermediate (down, chair)
Structure
MM2 Energy (kcal/mol)	54.37	48.16	48.92	44.34
MMFF94 Energy (kcal/mol)	76.30	66.35	70.53	60.56

As expected, the respective chair conformations of the intermediates 9 and 10 are lower in energy, compared to their twist boat analogues. The energy lost when going from the twist boat to the chair conformation is 5.45 kcal/mol for intermediate 9 (MM2), and 3.82 kcal/mol for intermediate 10. It is worth noting that intermediate 10 has a lower energy that intermediate 9 in both of the cyclohexane conformations, suggesting that the downward-pointing carbonyl group is preferred. This can be rationalised by the fact that when the carbonyl is pointing up, Van der Waals and bending related energies are lower, possibly due to the fact that in intermediate 9, the hydrogens on the isopropyl bridge come within 2.2 Å of the oxygen aton, whereas in intermediate 10, the nearest hydrogen is over 2.5 Å away. This is true for both the chair and the boat conformations.

Hyperstability

These alkenes are said to be hyperstable, a term coined by Maier and Schleyer in 1981. This term applies to bridghead olefins which resist hydrogenation, due to the higher stability of the olefin compared to the hydrogenated product. Maier and Schleyer also used a Olefin Stabilisation energy to compare the olefin to the hydrogenated product. Olefins with negative OS are said to be hyperstable. In the particular case of the 9 and 10 with the chair conformation of the cyclohexane ring, the OS are -23.99 and -23.43 kJ/mol (MOPAC/PM6), suggesting the olefins in question are hyperstable. Closer inspection of the hydrogenated products shows that the transannular strain is increased, compared to the unsaturated 9 and 10 analogues.

Modelling using semi-empirical Molecular Orbital Theory

Diene vs. Dihydro derivative

HOMO

LUMO

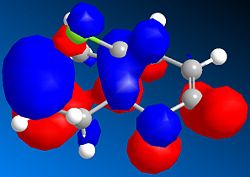
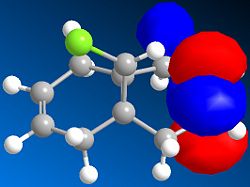
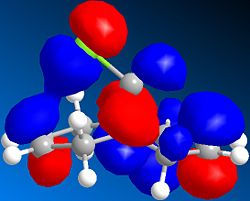
Basic MM2 energy optimisation of 12 results in a total energy of 17.90 kcal/mol. This compares relatively well to the MOPAC/PM6 heat of formation of 19.74 kcal/mol. The asymmetric nature of the molecule, due to the Cl atom lying above one ring, and the H atom above the other, means that the two C=C bonds will have different energies. MOPAC/PM6 calculations of the molecular surfaces enable us to identify which of the two olefins is the HOMO, and which is the LUMO. It turns out that the HOMO is mainly localised around the double bond lying below the Cl atom, as seen on the right. Consequently, the addition of dichlorocarbene, an electrophilic reagent, will selectively react with the HOMO, since as its name suggests, it is the highest occupied molecular orbital. This is largely supported experimentally, whereby molecule 12 reacts selectively with both dichlorocarbene and meta-chloroperbenzoic acid, two electrophilic reagents, to yield the anti adduct. Using similar reasoning, it can be predicted that the reaction of 12 with a nucleophilic reagent would lead to an addition onto the olefin anti to the Cl atom.

Vibrational frequencies can also be analysed in the gaussian input file format, to yield an output file which can be visuallised in Gaussview. This action (in the B3LYP/6-31G(d,p) format), was performed on molecule 12, as well as the dihydro derivative, with a double bond below the Cl atom. The latter minimises to an energy of 22.34 kcal/mol using MM2, and -2.43 kcal/mol using the MOPAC/PM6 model. The calculated C-Cl and C=C bonds are tabulated below.

Comparing Stretching Frequencies

C-Cl stretch (wavenumbers)	770.93	774.98
	548.78	501.30
	901.68	908.68
	930.08	925.85
C=C stretch (wavenumbers)	1757.42 (syn)	1785.07 (syn)
	1737.02 (anti)	-

12-dihydro derivative HOMO

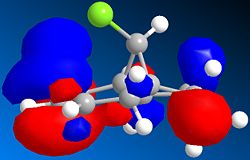
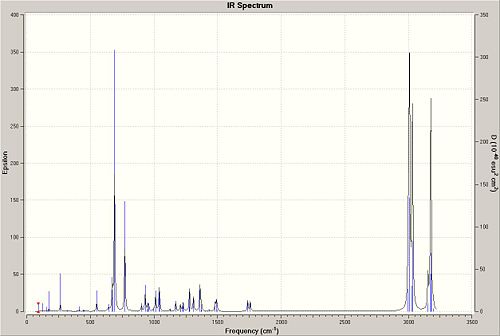
The first noteworthy observation is the loss of one C=C stretch upon hydrogenation. We also see that the remaining unsaturation, the C=C bond syn to the Cl atom, is found at higher wavenumbers, and hence is stronger than its unhydrogenated analogue. Closer inspection of the HOMO of both molecules provides a rationale for this observation. The HOMO of both molecules is mainly localised about the syn C=C bond, but the molecule 12 clearly interacts with the C-Cl bond in a π→σ^* fashion. This is seen more clearly in the HOMO-3 orbital, where the electron density on the C=C π orbital is actually merged with that of the Cl. This results in overall system stabilisation, since all 2 electron-based stereoelectronic interactions reduce the energy of the system, but also reduces the localisation of the π electrons involved in the C=C bond. In the dihydro derivative, this interaction is not present, as seen in the adjacent diagram, leading to a considerable increase in localisation of the π electrons, hence explaining the stronger C=C bond (as seen from the higher vibrational frequency). The variations in the major C-Cl stretches of both molecules (in bold) can be explained using the same reasoning. π→σ^* donation in molecule 12 leads to a reduced vibrational frequency, and hence a weaker C-Cl bond. In the dihydro derivative, the σ^* orbital is unpopulated, so the C-Cl interaction is a 2 electron interaction, thus strengthening the bond.

Spectrum of 12	Spectrum of dihydro-12

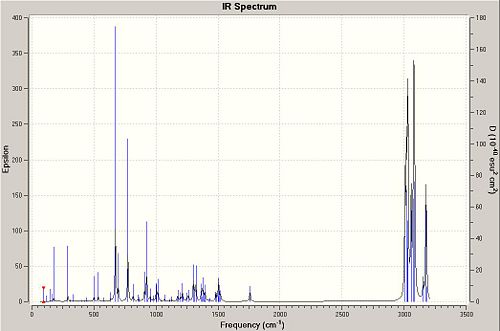
Effect of substituents

12 HOMO-3

Theory predicts that the functional group attached to the alkenes will affect the nature of the bond, such as its energy, and its shape. Electronegative elements have atomic orbitals which lay deeper in energy that electropositive elements. Consequently, one would expect that the addition of an electronegative atom close to a double bond would lead to an inductive withdrawal of electron density from the double bond. Delocalisation of a lone pair from a heteroatom into the π^* orbital of the double bond is also predicted. We would thus expect a reduction in the strength of the C=C bond (lower wavenumbers). To verify these statements, hydroxyl derivatives of compound 12 are studied below.

Two different derivatives were studied, both containing a hydroxyl group attached to one of the olefins. The first compound, 12ha, contains a hydroxyl group on the C=C exo (Anti) to the Cl, and the second, 12hb, contains a hydroxyl group on the C=C endo (syn) to the Cl. From these two compounds we can explore both the effect of the hydroxyl group on the C=C bonding, as well as its influence, if any, on the C-Cl bonding.

12ha HOMO-3

Streching frequencies (wavenumbers)

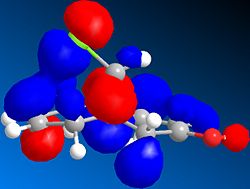
C=C (Exo)	1737.02	1753.02	1737.62
C=C (Endo)	1757.42	1757.74	1799.86
C-Cl	770.93	765.30	765.23

Contrary to what was expected, the C=C bond exo to the Cl atom was made stronger upon addition of the hydroxyl group (12a). Close inspection of the molecular orbitals shows that the HOMO of 12ha has the majority of its electron density smeared over the two atoms involved in π bonding. The rest is spread more or less equally across the hydroxyl group and the carbon in the 1 position on the other side of the olefin. On the other hand, the endo C=C bond strength is unaffected by the addition of the substituent on the exo C=C. However, it seems that its donation into the C-Cl σ^* orbital is enhanced, since the stretching frequency of the C-Cl bond is reduced. Furthermore, the HOMO-3 involved in this interaction in both 12 and 12ha shows a slightly larger overlap in the 12ha compound, thus explaining the spectroscopic changes. 12b also shows results which disagree with the predictions. The substituted double bond is significantly strengthened, and the C-Cl bond is weakened. As for 12a, the molecular orbital of the substituted C=C bond shows most of its electron density on the C=C bond, rather than on the expected delocalisation along the C-C-O bonds. The weakening of the C-Cl bond is a little less understood, since it does not seem to interact with the C=C bond as in 12 and 12a. The reason why the oxygen lone-pairs do not interact with the π^* orbital of the C=C as much as expected can probably be due to the high strain that is present in the extreme resonance form, with a ketone and a C-C bond. Therefore, lone pair donation is inhibited.

Mini Project - Opening of trans-1,2,4,5-diepoxycyclohexane using N-methyl aniline

Introduction

The reaction to be studied appears a paper by C.J. Monceaux et al., and involves the succesive opening of two trans orientated 1,2 and 4,5 epoxides on a cyclohexane ring, using a secondary amine. The paper explores the effect of the amine substituents on the regiochemistry of the reaction, thus building on the Fürst-Plattner rule. Epoxides are very synthetically useful because they allow chemists to control the stereochemistry about the two carbon atoms involved in the 3-membered ring. Epoxides with less than 4 substituents rarely require forcing methods, and due to the driving force of the release of ring strain, are generally quite reactive. Epoxides contain very electrophilic carbon atoms, which are subject to nucleophilic attack, which, in most circumstances, occurs in a bimolecular fashion (S_N2). Since S_N2 reactions proceed via inversion of configuration at the electrophilic centre, nucleophilic attacks on epoxides also lead to an inversion. Knowledge of this is essential in predicting the product of the reactions of an epoxide. The next factor to take into account to predict the outcome of the reaction is the regioselectivity of the attack. Attempting to explain the strong regioselectivity of the above reaction, and to predict the geometry/conformations of the products is the focus of this project.

Analysis of intermediate conformations and their influence on regiocontrol

Reactant Basic MM2 analysis of 1,2,4,5-diepoxycyclohexane shows that the preferred conformation of the diepoxide is the trans form, although the difference in energy between the two is minimal (199.32 kcal/mol for the trans isomer, versus 200.48 kcal/mol for the cis isomer). Similarly, MOPAC/PM6 calculations proposed the trans conformer as the most stable, with a difference of approx. 0.4 kcal/mol between the two conformers.

Intermediates MM2 analysis of the two intermediates which dictate the regioselectivity of the reaction (the epoxy aminoalcohol in the diaxial and diequatorial conformations) shows what one expects: the diequatorial intermediate is much more stable than the diaxial analogue. This is rationalised by the increased 1,3-diaxial compression in the diaxial conformation. Attack of the methylated aniline on the diepoxide reactant leads a racemic mixture of the diaxial intermediate. The racemic nature of the reaction is due to the uncontrolled attack on either of the carbons of the epoxide. The σ_h nature of the reactant means that the two carbon centres are equivalent, so nucleophilic attack is equally likely for both. The reason a diaxial intermediate is formed is due to the stereoelectronic constraints of the nucleophilic attack. The regioselectivity of the second attack of N-methyl aniline depends on the conformation of the epoxide substrate at the time of the attack. The two conformations (diaxial and diequatorial) are in equilibrium, although the diequatorial intermediate is largely preferred, making the diaxial conformer short lived. Consequently, the 1,3-diol is selectively produced, unless the incoming nucleophile is a suitable hydrogen bond donor, whereby the 1,4-diol is produced. The reason for this is explained in the mechanistic study below.

Intermediates

Diaxial	Diequatorial

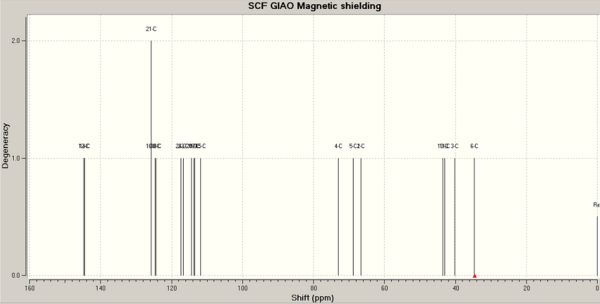
¹³C NMR: Calculated versus experimental

1,3 diol

In order to calculate the ¹³C NMR of the 1,3 diol and compare it to the value given in the literature, the conformation of the compound must be optimised. The first conformation to be tested was drawn out on ChemBio3D, and its energy was minimised using MM2. The conformation was further refined using Gaussian and a mpw1pw91/6-31(d,p) model. The final conformation, although little was changed compared to the MM2 minimised structure, had an energy of 167.91 kJ/mol (MM2): .

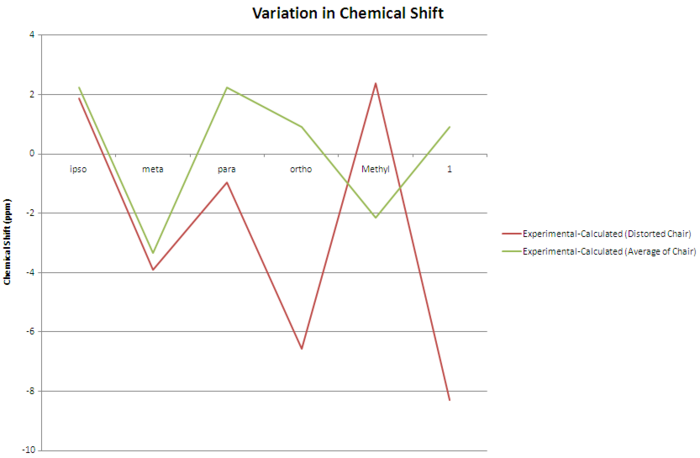
The ¹³C NMR was calculated using the mpw1pw91/6-31(d,p) model again, in the same solvent as indicated in the literature (methanol). As can be seen from the plot of the calculated chemical shifts versus the experimental/literature values, the calculated values are generally quite far off from the experimental ones, suggesting that the proposed conformation is not the correct one.

Cyclohexane rings are usually capable of ring-flip at room temperature, if the two conformations are close enough in energy. The literature suggests that this ring flipping is responsible for the single signal observed for C1 and C3, as well as the one observed for C4 and C6. Since it is not possible to calculate a time-averaged structure, the two extreme chair conformations were drawn, their energies minimised and their ¹³C NMR calculated using the method previously described. The resulting chemical shifts were averaged for each carbon environment described in the literature, and compared to the experimental values. The fit is now much improved compared to the previous conformation. The average difference between the calculated and observed chemical shifts is reduced from 5.95 to 3.74 ppm, and the maximum difference is now 8.93 ppm compared to 12.08 ppm.

The two 'extreme' conformations used for the calculation are shown in the table below, with their corresponding energies and jmol file. MOPAC/PM6 calculations indicates a relative energy difference of 6.56 kJ/mol, which is quite close in magnitude to RT, but does not fully support the statment that the two extreme conformations readily isomerise at room temperature. However, the close match of the calculated ¹³C NMR with the literature values does tend to confirm the rapid equilibrium, indicating that the relative energy gap between the two conformers is most likely smaller than the calculated value.

Extreme chair conformations

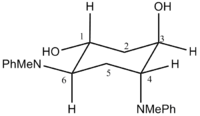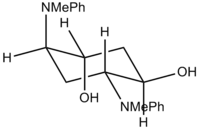
	MM2 (kJ/mol)	206.03		150.65
	MOPAC/PM6 Energies (kJ/mol)	-48.05		-46.48

¹³C NMR Data

	Distorted Chair			Average Chair
Substituent	Calculated (ppm)	Experimental (ppm)	Difference (ppm)	Calculated (ppm)	Experimental (ppm)	Difference (ppm)
ipso	141.34	153.42	12.08	144.49	153.42	8.93
meta	125.56	130.13	4.57	125.48	130.13	4.65
para	112.59	121.38	8.80	114.22	121.38	7.16
ortho	110.48	120.15	9.67	113.07	120.15	7.08
methyl	43.41	37.08	-6.33	38.62	37.08	-1.54
C1	65.96	67.82	1.86	65.58	67.82	2.24
C2	41.08	37.16	-3.92	40.52	37.16	-3.36
C3	68.77	67.82	-0.95	65.58	67.82	2.24
C4	68.61	62.05	-6.56	61.15	62.05	0.90
C5	23.34	25.72	2.38	27.88	25.72	-2.16
C6	70.36	62.05	-8.31	61.15	62.05	0.90

1,4 diol

The 1,4 diol product, if it was formed, would do so as a single stereoisomer, for mechanistic reasons. From basic MM2 calculations, it is predicted that it would exist only as the conformer with all its substituents in the equatorial positions: In fact, the conformation in which all the substituents are axial is highly energetically disfavoured, and it is not possible to obtain its structure and minimise it using ChemBio3D and MM2. Consequently, it is safe to assume that the ¹³C NMR of the 1,4 diol will not be a time averaged spectrum of the two conformations, but that of the single, all-axial conformer. The ¹³C NMR of this structure was calculated using the same method as for the 1,3 diol, and is shown below.

¹³C NMR 1,4 diol

Unfortunately, the ¹³C NMR of the product was not included in the supplementary material of the paper, since the reaction was completely selective for the 1,3 diol. Nevertheless, given that the predictions for the 1,3 diol were within an acceptable range of the literature values, and that the 1,4 diol is predicted to exist as a single conformer, it can safely be said that the calculated ¹³C NMR will also be within an acceptable range.

³J_HH Coupling: Calculated versus experimental

The Karplus equation provides a simple yet accurate way of predicting the 3J coupling of protons form the dihedral angle between them. The coupling constants for each proton in both of the 1,3 diol conformations (2 and 3) were computed from the dihedral angle using the Janocchio plugin. From this, knowing that the two conformations readily interconvert, the coupling constants were averaged over both structures. The results are very accurate, with all the coupling constants being within 0.3 Hz of the literature values.

Dihedral Angle	3JHiHj (hz)	Hi	Hj				Dihedral Angle	3JHiHj (hz)	Hi	Hj
-168.4	11.2	3	1				-73.2	1.9	1	3
-53.7	4.5	2	1				43.4	4.9	1	2
169.3	8.3	8	1				73.9	2.0	1	8
34.9	6.3	4	3				-66.9	2.7	3	4
-78.8	1.5	4	2				175.5	11.7	2	4
72.6	2.1	5	4				-177.3	9.2	5	4
-56.5	4.3	6	5				-172.2	11.0	5	6
60.1	1.9	7	5				-57.5	4.4	7	5
-56.3	4.6	8	6				52.3	2.8	6	8
-172.2	11.0	8	7				-64.5	3.2	7	8

Since both chairs are readily interconverting, H1=H4, H2=H3, H5=H8, and H6=H7. Consequently, the time-averaged spectrum is expected to show four signals for each pair of hydrogens on the cyclohexane ring, each with an integral of 2H. H1/H4 is expected to appear as a doublet of triplets, coupling to H8/H5 and two identical protons H3 and H2. Similarly, H5/H8 are expected to be a doublet of triplets, due to coupling to H1/H4, and two identical protons H6 and H7. H2/H3 are expected to manifest themselves as a triplet, coupling to two identical protons H1 and H4. Finally, H6/H7 are also expected as a triplet resulting from coupling to two identical protons H5 and H8. A multiplet is also expected in the range of 7.2-6.5 ppm for the aniline protons (lower ppm than free benzene due to the electron donating nature of the amine group), with an integral of 10H. Finally, a singlet at about 4.5 ppm, with an integral of 6H is expected for the methyl protons on the amine. The predicted spectrum of the 1,3 diol (cyclohexane protons only) compared to the reported experimental spectrum is shown below.

Position	Predicted	Experimental
H1/H4	dt, J 5.6 Hz	q, J 5.8 Hz
H5/H8	dt, J 5.5 Hz	q, J 5.8 Hz
H2/H3	t, J 5.6 Hz	t, J 5.6 Hz
H6/H7	t, J 5.5 Hz	t, J 5.6 Hz

It can be seen here that the predicted coupling constants are very close to the literature values, with the largest difference being 0.3 Hz. This is an acceptable error, and having such predictions can be invaluable when identifying the product, as well as to ascertain the conformation of this product. The predicted multiplicities of H1/H4 and H5/H8 do not match the ones observed in the literature, but this is most likely due to the very small difference in coupling constants between the double and the triplet, which therefore overlap to form an apparent quartet.

Unfortunately, the aromatic protons were not modeled as well, with predicted coupling constants of 8.2 Hz, rather than the observed 7.9 and 7.2 Hz. This is still acceptable, although not as conclusive as the cyclohexane protons. This issue is not very important due to the lack of signals of protons other than aromatic ones in the range of 7.5-6.5. Furthermore, coupling constants for aromatic protons are generally of the order of 8 Hz. I speculate that if large deviations from this occur, this indicates that the hybridisation of the aromatic carbons is no longer sp², and aromaticity may be reduced. This would also manifest itself in an upfield shift of the signals, due to reduced ring currents.

Optical rotation of the 1,4 diol

In order to verify the validity of the proposed strucutre for the 1,4 diol, the method of 3JHH coupling used for the 1,3 diol is also appropriate, and will probably be more conclusive, since it will not be time averaged. However, optical rotation is also very much affected by the conformation of the molecule. As for the proton NMR, no data of this type is available from the literature, but the optical rotation of the 1,4 diol was computed for possible comparison with future studies. An initial calculation was run with basis set aug-cc-pvdz. Unfortunately, this failed to converge, and so the calculation was repeated with the more simple 6-31G(d,p) basis set, to give [α] (5890.0 Å) = -49.35 deg.

Reaction Mechanism and its implications

H-Bonding stabilising the diaxial intermediate with primary amines as nucleophiles

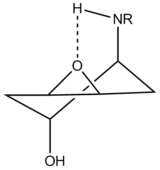
The initial nucleophilic attack of the amine on the epoxide leads to a racemic trans diaxial intermediate, due to the Fürst-Plattner rule. The diaxial intermediate is prefered, even though it is less stable, because it proceeds via a transition state which has the chair form. If the diequatorial intermediate was formed directly, it would have to proceed via a high energy transition state of the twist boat type. The trans diaxial intermediate can then reversibly ring flip to the more stable trans diequatorial conformer. The regiochemistry of the final product, either 1,3 or 1,4 diol, is dictated by the conformation that the intermediate is in at the moment of attack. The stereochemistry of the product is then dictated by the Fürst-Plattner rule once again. The epoxide ring opening at each step is aided by the activation of the epoxide through protonation/hydrogen bonding. This is done by any trace acid, protic solvent, or possibly intramolecularly (for primary amine nucleophiles). In the latter case, the intramolecular hydrogen bond stabilises the diaxial intermediate, and directs nucleophilic attacks to yield the 1,4 diol. This is referred to as the NH-directed Fürst-Plattner attack. The mechanism for the reaction is shown below.

Conclusions

Identification of the 1,3 and 1,4 diols from their individual ¹³C NMR would be quite easy, provided that predicted spectrum was computed. Otherwise, the similarity between the two products, added to the very similar inductive effects of the hydroxyl and aniline groups, would mean that differentiating between the two products from the ¹³C NMR only would be quite difficult. Only possible option in such a case would be to realise that the 1,4 diol is not a time averaged spectrum of the flipping chair (as for the 1,3 diol), and as such would exhibit a greater number of signal. A similar reasoning is possible for the ¹H NMR, where the time averaging of the two conformations in the 1,3 diol leads to only 4 signals for the cyclohexane protons, as opposed to a predicted 8 for the 1,4 diol. In addition, analysis of ³J_HH coupling allows us to accurately describe the product's conformation. Hence a combination of both NMR spectra would enable easy differentiation between the products, and insight into the possible conformations they adopt. This is a viable option since the two products are easily separable by flash column chromatography as stated in the literature. The conformation of the 1,4 diol could be further analyzed by comparing the calculated optical rotation with an experimentally observed one.

---

References