Rep:Mod:origskgroup
Introduction
This module aims to use computational chemistry to study the molecular reaction dynamics of the Cope rearrangement and Diels-Alder reactions by investigating the structures of the possible transition states which arise. This will involve solving the Schrodinger equation using various numerical methods in order to identify these transition states by their potential energy surfaces and the key features within these surfaces (i.e. reaction paths and barrier heights, as well as total energies). Note that the methods applied here are different to those used for studying molecular reaction dynamics for simple diatomics and triatomics, as the molecules involved in these systems are much smaller and simpler than those being studied in this work (e.g. conjugated systems and longer chain molecules); standard mechanics cannot be applied to these larger molecules as the method does not account for changes in bonding or electron distribution, nor does it describe the formation/breaking of bonds. Consequently, molecular orbital-based methods are applied to more complicated systems.
The Cope Rearrangement
This reaction is a [3,3] sigmatropic rearrangement and this section of the work involves identifying the preferred reaction mechanism by using computational methods as described in the introduction.
Optimisation of reactants and products
Optimising anti-periplanar ("anti") 1,5-hexadiene
Optimised ("anti") 1,5-hexadiene results.
File Type: .log Calculation Type: FOPT Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.69253528 a.u. RMS Gradient Norm: 0.00001891 a.u. Imaginary Freq Dipole Moment: 0.0000 Debye Point Group: C1 Job CPU time: 0 days 0 hours 1 minutes 18.3 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000060 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000422 0.001800 YES
RMS Displacement 0.000171 0.001200 YES
Predicted change in Energy=-2.036702D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.69253528 a.u.
Frequency analysis was carried out on the optimised structure to confirm that a minimum energy had indeed been obtained:
("anti") 1,5-hexadiene frequency analysis results.
File Type: .log Calculation Type: FREQ Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.69253528 a.u. RMS Gradient Norm: 0.00001870 a.u. Imaginary Freq: 0 Dipole Moment: 0.0000 Debye Point Group: C1 Job CPU time: 0 days 0 hours 0 minutes 26.1 seconds.
The results file for the frequency analysis is linked to here.
Low frequencies --- -5.7089 -2.3468 -2.0786 -0.0010 -0.0009 -0.0009 Low frequencies --- 71.2021 85.6862 116.1470
The second line of the above frequency table contains no negative values, confirming that a minimum has been reached and therefore the structure is not a transition state. The first line of the table contains values that are in close proximity to zero (i.e. within ±15 cm-1), also confirming that the structure is not a maximum (i.e. transition state) but indeed a minimum.
Optimising gauche 1,5-hexadiene
Optimised gauche 1,5-hexadiene results.
File Type: .log Calculation Type: FOPT Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.68302540 a.u. RMS Gradient Norm: 0.00003415 a.u. Imaginary Freq Dipole Moment: 0.3650 Debye Point Group: CS Job CPU time: 0 days 0 hours 1 minutes 28.3 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000080 0.000450 YES
RMS Force 0.000020 0.000300 YES
Maximum Displacement 0.000485 0.001800 YES
RMS Displacement 0.000186 0.001200 YES
Predicted change in Energy=-9.066649D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.68302540 a.u.
Frequency analysis was carried out on the optimised structure to confirm that a minimum energy had indeed been obtained:
gauche 1,5-hexadiene frequency analysis results.
File Type: .log Calculation Type: FREQ Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.68302540 a.u. RMS Gradient Norm: 0.00003406 a.u. Imaginary Freq: 1 Dipole Moment: 0.3650 Debye Point Group: CS Job CPU time: 0 days 0 hours 0 minutes 26.9 seconds.
The results file for the frequency analysis is linked to here.
Low frequencies --- -4.8026 -3.2707 -2.2973 0.0004 0.0006 0.0022 Low frequencies --- 1.5722 78.1661 111.3123
Investigating lower energy conformers of 1,5-hexadiene
In order to confirm which conformer was lowest in energy, various different conformations were created and optimised at the same level of theory as that used above so that the energy values could be directly compared.
| Conformer | Total energy (a.u.) | Published results |
| gauche2 | -231.69166702 | gauche2 |
| gauche3 | -231.69266119 | gauche3 |
| anti1 | -231.69260236 | anti1 |
| anti2 | -231.69253528 | anti2 |
The above data confirms that the lowest energy conformer of 1,5-hexadiene is the gauche3; this observation is consistent with the data given in the appendix of the script.
Analysis of "anti2" 1,5-hexadiene
The anti2 conformer was examined more closely, having already been optimised earlier in this work using the 3-21G (low-level) basis set. This structure was re-optimised using the slightly more accurate 6-31G basis set.
Optimised ("anti2") 1,5-hexadiene results.
File Type: .log Calculation Type: FOPT Calculation Method: RB3LYP Basis Set: 6-31G(d) Charge: 0 Spin: Singlet E(RB3LYP): -234.61172262 a.u. RMS Gradient Norm: 0.00001106 a.u. Imaginary Freq Dipole Moment: 0.0000 Debye Point Group: Ci Job CPU time: 0 days 0 hours 3 minutes 26.4 seconds.
The optimisation file (using the 6-31G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000013 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000180 0.001800 YES
RMS Displacement 0.000073 0.001200 YES
Predicted change in Energy=-1.274077D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 6-31G optimised structure = -234.61172262 a.u. Note that this value is in agreement the data given in the appendix, and that this value is lower in energy than the value obtained at the lower level of accuracy. The other key point to observe is that the geometry of the structure has changed slightly following the optimisation at the higher level of accuracy; this is reflected by the change in point group of the conformer from C1 to Ci.
Frequency calculation was performed on the optimised structure to again confirm that a minimum energy had been obtained, but also to investigate the associated thermochemistry of the conformer:
("anti2") 1,5-hexadiene frequency analysis results.
File Type: .log Calculation Type: FREQ Calculation Method: RB3LYP Basis Set: 6-31G(d) Charge: 0 Spin: Singlet E(RB3LYP): -234.61172262 a.u. RMS Gradient Norm: 0.00001100 a.u. Imaginary Freq: 0 Dipole Moment: 0.0000 Debye Point Group: Ci Job CPU time: 0 days 0 hours 3 minutes 27.7 seconds.
The results file for the frequency analysis is linked to here.
Low frequencies --- -10.1580 0.0007 0.0007 0.0008 9.7672 18.7940 Low frequencies --- 74.0081 80.9085 123.3428
Sum of electronic and zero-point Energies = -234.469174 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -234.461835 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -234.460890 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -234.500736 a.u. (G = H - TS)
Note that within the four values given in the thermochemistry data, all but the first include very small corrections in order to account for various contributions of enthalpic and entropic nature.
Optimisation of "chair" and "boat" conformers of transition states
Optimisation of allyl fragment
Optimised allyl fragments results.
File Type: .log Calculation Type: FOPT Calculation Method: UHF Basis Set: 3-21G Charge: 0 Spin: Doublet E(UHF): -115.82303991 a.u. RMS Gradient Norm: 0.00009674 a.u. Imaginary Freq Dipole Moment: 0.0293 Debye Point Group: C1 Job CPU time: 0 days 0 hours 0 minutes 35.1 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000160 0.000450 YES
RMS Force 0.000056 0.000300 YES
Maximum Displacement 0.000711 0.001800 YES
RMS Displacement 0.000290 0.001200 YES
Predicted change in Energy=-1.860815D-07
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -115.82303991 a.u.
Optimising the "chair" conformation
Optimisation - Hessian method
Hessian-optimised "chair" TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.61932247 a.u. RMS Gradient Norm: 0.00000692 a.u. Imaginary Freq: 1 Dipole Moment: 0.0001 Debye Point Group: C2h Job CPU time: 0 days 0 hours 0 minutes 35.2 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000313 0.001800 YES
RMS Displacement 0.000060 0.001200 YES
Predicted change in Energy=-8.025162D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.61932247 a.u.
Sum of electronic and zero-point Energies = -231.466701 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -231.461341 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -231.460397 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -231.495207 a.u. (G = H - TS)
Low frequencies --- -817.9365 -1.3903 0.0002 0.0006 0.0008 1.5494 Low frequencies --- 2.5968 209.5447 395.9286 ****** 1 imaginary frequencies (negative Signs) ******
The one imaginary frequency is observed at -817.9365 cm-1 and this vibration is animated below in order to confirm that it does indeed correspond to the Cope rearrangement:
Optimisation - Frozen coordinate method
Frozen coordinate-optimised "chair" TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.61932247 a.u. RMS Gradient Norm: 0.00000692 a.u. Imaginary Freq: 1 Dipole Moment: 0.0001 Debye Point Group: C2h Job CPU time: 0 days 0 hours 0 minutes 35.8 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000313 0.001800 YES
RMS Displacement 0.000060 0.001200 YES
Predicted change in Energy=-8.025162D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.61932247 a.u.
Sum of electronic and zero-point Energies = -231.466701 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -231.461341 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -231.460397 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -231.495207 a.u. (G = H - TS)
Low frequencies --- -817.9365 -1.3903 -0.0007 -0.0007 -0.0004 1.5494 Low frequencies --- 2.5968 209.5447 395.9286 ****** 1 imaginary frequencies (negative Signs) ******
Again, one imaginary frequency is observed at -817.9365 cm-1 and the animation below confirms that it corresponds to the Cope rearrangement:
Comparing optimisations
Comparison of the results from the Hessian and frozen coordinate methods shows that the exact same data is obtained, irrespective of the method applied. This is observed for the key values of total electronic energy, imaginary frequency and the thermochemistry data values.
Optimising the "boat" conformation
The "boat" conformation was optimised using the QST2 method. The first attempt at doing this by applying this method to the initially drawn reactant and product structures immediately failed, as the calculation failed to account for the possibility of rotation around the central carbon-carbon bonds. Consequently, it was necessary to restrict the geometries of both the reactant and product structures in order to produce a set of input structures for the calculation that vaguely resembled something like the "boat" conformation trying to be achieved. This calculation proved to be much more successful:
QST2-optimised "boat" TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.60280244 a.u. RMS Gradient Norm: 0.00001207 a.u. Imaginary Freq: 1 Dipole Moment: 0.1584 Debye Point Group: C2v Job CPU time: 0 days 0 hours 0 minutes 34.8 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000031 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001671 0.001800 YES
RMS Displacement 0.000524 0.001200 YES
Predicted change in Energy=-4.845339D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.60280244 a.u.
Sum of electronic and zero-point Energies = -231.450929 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -231.445301 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -231.444356 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -231.479774 a.u. (G = H - TS)
Low frequencies --- -840.1095 -0.0007 -0.0007 0.0005 1.7194 2.3084 Low frequencies --- 4.6293 155.3437 382.0939 ****** 1 imaginary frequencies (negative Signs) ******
One imaginary frequency is observed at -840.1095 cm-1 and the animation below illustrates that it represents the Cope rearrangement proceeding via the "boat" conformation:
Investigating reaction paths - Intrinsic Reaction Coordinate (IRC) method
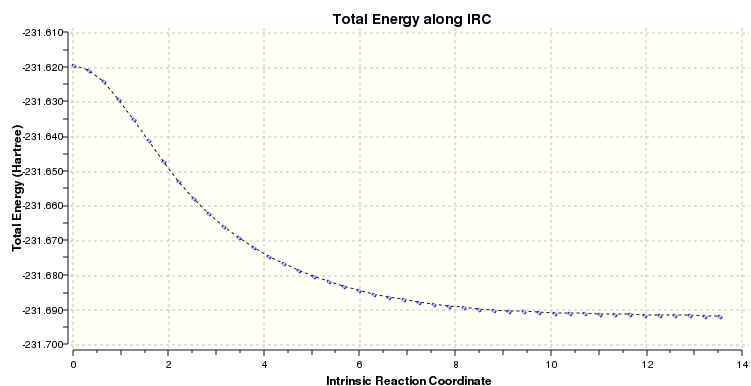
Optimising the transition state structures gives an accurate representation of their conformations, however it does not allow us to easily identify which conformers of the reactant and product have been involved in the reaction path. The IRC method allows us to analyse the potential energy surface and track the minimum energy reaction path from a given transition state to its local minimum point. To illustrate this, the IRC method was applied to the Hessian-optimised "chair" conformation TS:
Hessian-optimised "chair" TS IRC results.
Below shows a results summary for the final structure:
File Type: .log Calculation Type: IRC Calculation Method: Basis Set: Charge: 0 Spin: Singlet E(RHF): -231.69157890 a.u. RMS Gradient Norm: 0.00015225 a.u. Imaginary Freq Dipole Moment: 0.3631 Debye Point Group: C2 Job CPU time: 0 days 0 hours 20 minutes 57.3 seconds.
The IRC file is linked to here.
Total energy for final structure = -231.69157890 a.u.
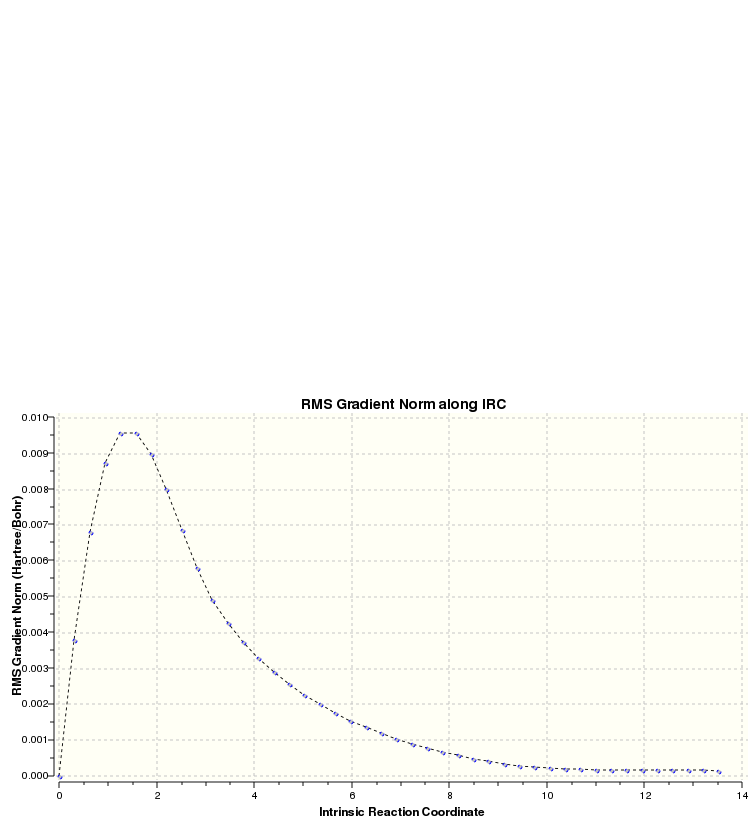
The above graph shows how the reaction coordinate appears to reach a minimum but upon closer examination it is observed that the gradient is not absolutely flat as required.
This graph showing the gradient confirms that a minimum has not quite been reached, as previously mentioned. There are three ways in which further calculation can be performed in order to obtain the desired minimum:
- Perform an optimisation of the final structure obtained from the original IRC method
- Apply the IRC method again, specifying a greater number of points
- Apply the IRC method again, specifying the computation of force constants at every step
In this instance, the first option was chosen and applied as both the second and third options require the repetition of the IRC calculation which is time-consuming in comparison to an optimisation:
Optimised final structure results.
File Type: .log Calculation Type: FOPT Calculation Method: RHF Basis Set: 3-21G Charge: 0 Spin: Singlet E(RHF): -231.69166702 a.u. RMS Gradient Norm: 0.00000475 a.u. Imaginary Freq Dipole Moment: 0.3806 Debye Point Group: C2 Job CPU time: 0 days 0 hours 1 minutes 3.0 seconds.
The optimisation file (using the 3-21G basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000300 0.001800 YES
RMS Displacement 0.000091 0.001200 YES
Predicted change in Energy=-2.409654D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 3-21G optimised structure = -231.69166702 a.u.
Calculation of activation energies
The activation energies for the reactions via the two different transition states can be calculated by taking the difference in energy between the optimised transition state structure and the optimised product structure. However in order to allow an accurate calculation, it is necessary to obtain optimised transition state structures with an improved accuracy. Consequently, both transition state conformations were re-optimised at the 6-31G* level before calculating the activation energy.
Reaction via "chair" conformation
Hessian-optimised "chair" TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RB3LYP Basis Set: 6-31G(d) Charge: 0 Spin: Singlet E(RB3LYP): -234.55698303 a.u. RMS Gradient Norm: 0.00001252 a.u. Imaginary Freq: 1 Dipole Moment: 0.0000 Debye Point Group: C2h Job CPU time: 0 days 0 hours 6 minutes 6.3 seconds.
The optimisation file (using the 6-31G* basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000027 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000109 0.001800 YES
RMS Displacement 0.000036 0.001200 YES
Predicted change in Energy=-5.360546D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 6-31G* optimised structure = -234.55698303 a.u.
Sum of electronic and zero-point Energies = -234.414929 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -234.409008 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -234.408064 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -234.443814 a.u. (G = H - TS)
Low frequencies --- -565.5341 -0.0002 0.0003 0.0005 21.8423 27.2470 Low frequencies --- 39.6911 194.4983 267.9719 ****** 1 imaginary frequencies (negative Signs) ******
The activation energy for this reaction path was then calculated:
E("chair" TS) = -234.55698303 a.u.
E(product) = -234.61172262 a.u.
Therefore:
ΔE = E("chair" TS) - E(product)
ΔE = -234.55698303 - (-234.61172262)
ΔE = +0.05473959 a.u.
ΔE = +34.349618665 kcal mol-1
It should be noted that the above value obtained is in close agreement with the experimental values quoted (+33.5 ± 0.5 kcal mol-1).
Reaction via "boat" conformation
Optimised "boat" TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RB3LYP Basis Set: 6-31G(d) Charge: 0 Spin: Singlet E(RB3LYP): -234.54309304 a.u. RMS Gradient Norm: 0.00000867 a.u. Imaginary Freq: 1 Dipole Moment: 0.0614 Debye Point Group: C2v Job CPU time: 0 days 0 hours 5 minutes 57.3 seconds.
The optimisation file (using the 6-31G* basis set) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000017 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000755 0.001800 YES
RMS Displacement 0.000191 0.001200 YES
Predicted change in Energy=-3.596575D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for 6-31G* optimised structure = -234.54309304 a.u.
Sum of electronic and zero-point Energies = -234.402339 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = -234.396005 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = -234.395061 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = -234.431748 a.u. (G = H - TS)
Low frequencies --- -530.5704 -8.0860 -0.0009 -0.0008 -0.0008 15.1616 Low frequencies --- 17.3752 135.5547 261.8483 ****** 1 imaginary frequencies (negative Signs) ******
The activation energy for this reaction path was then calculated:
E("boat" TS) = -234.54309304 a.u.
E(product) = -234.61172262 a.u.
Therefore:
ΔE = E("boat" TS) - E(product)
ΔE = -234.54309304 - (-234.61172262)
ΔE = +0.06862958 a.u.
ΔE = +43.065720845 kcal mol-1
It should be noted that the above value obtained is in close agreement with the experimental values quoted (+44.7 ± 2.0 kcal mol-1).
The Diels-Alder Cycloaddition
This section focuses on this simple cycloaddition reaction involving a diene and a dieneophile. Initially, one of the most simple examples will be studied here, namely the reaction between ethene and cis-butadiene to produce cyclohexene. Subsequent work will then be carried out to investigate regioselectivity and its associated energetics within these Diels-Alder reactions; the case study used here is the reaction between cyclohexa-1,3-diene and maleic anhydride.
Ethene and cis-butadiene
Optimisation of cis-butadiene
AM1-optimised cis-butadiene results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): 0.04879718 a.u. RMS Gradient Norm: 0.00001402 a.u. Imaginary Freq: 1 Dipole Moment: 0.0414 Debye Point Group: C2 Job CPU time: 0 days 0 hours 0 minutes 8.4 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000025 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000539 0.001800 YES
RMS Displacement 0.000214 0.001200 YES
Predicted change in Energy=-8.826151D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = 0.04879718 a.u.
Sum of electronic and zero-point Energies = 0.134553 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = 0.138573 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = 0.139518 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = 0.108518 a.u. (G = H - TS)
Low frequencies --- -40.0454 -6.1202 -3.6149 -2.3259 -0.0004 0.0435 Low frequencies --- 0.0605 312.4530 485.1690 ****** 1 imaginary frequencies (negative Signs) ******
The HOMO and LUMO MOs involved in the reaction are shown below:
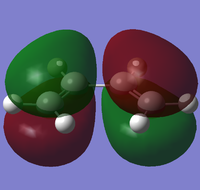HOMO - anti-symmetric with respect to the plane; contains one node
LUMO - symmetric with respect to the plane; contains two nodes
Optimisation of ethene
AM1-optimised ethene results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): 0.02619028 a.u. RMS Gradient Norm: 0.00003483 a.u. Imaginary Freq: 0 Dipole Moment: 0.0000 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 11.5 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000170 0.000450 YES
RMS Force 0.000051 0.000300 YES
Maximum Displacement 0.000454 0.001800 YES
RMS Displacement 0.000234 0.001200 YES
Predicted change in Energy=-4.166419D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = 0.02619028 a.u.
Sum of electronic and zero-point Energies = 0.077198 a.u. (E = Eelect + ZPE) at 0K Sum of electronic and thermal Energies = 0.080252 a.u. (E = Evib + Erot + Etrans) under standard conditions Sum of electronic and thermal Enthalpies = 0.081196 a.u. (H = E + RT) Sum of electronic and thermal Free Energies = 0.055005 a.u. (G = H - TS)
Low frequencies --- -0.0003 -0.0002 -0.0001 14.8633 16.3757 16.6918 Low frequencies --- 834.5379 874.2388 1056.2871
The HOMO and LUMO MOs involved in the reaction are shown below:
HOMO - symmetric with respect to the plane; contains no nodes
LUMO - anti-symmetric with respect to the plane; contains one node
HOMO and LUMO interactions
Molecular orbitals of the same symmetry (i.e. both symmetric or both anti-symmetric) can interact favourably. Applying this to ethene and cis-butadiene, comparison of the HOMO and LUMO MOs shows that the HOMO of one reactant interacts favourably with the LUMO of the other reactant and vice versa. This will also be illustrated in the example of the Diels-Alder transition state, which follows below.
The Diels-Alder transition state
AM1-optimised TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): 0.11165466 a.u. RMS Gradient Norm: 0.00001989 a.u. Imaginary Freq: 1 Dipole Moment: 0.5605 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 8.8 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = 0.11165466 a.u.
Low frequencies --- -956.6652 -0.0842 -0.0430 -0.0032 0.5813 2.5576 Low frequencies --- 3.3086 147.2431 246.5734 ****** 1 imaginary frequencies (negative Signs) ******
The above frequency analysis table shows that one imaginary frequency is observed at -956.6652 cm-1 and this confirms the presence of a transition state. The vibration is animated below in order to confirm that it does indeed correspond to the Diels-Alder cycloaddition:
The main geometric features of the optimised transition state involve the formation of the double bond (shown as a dashed bond in the transition state). The animation also confirms that the formation of the two new carbon-carbon bonds is synchronous via the above transition state. The geometry of the transition state is discussed further below.
As previously mentioned, the HOMO-LUMO region is the area of importance for understanding this reaction. The image below illustrates the anti-symmetric HOMO of the optimised transition state:
The above HOMO is formed from interactions between the anti-symmetric HOMO of cis-butadiene and the anti-symmetric LUMO of ethene as shown below:
HOMO of cis-butadiene
LUMO of ethene
As expected, combination of two anti-symmetric MOs results in retention of orbital symmetry, as shown in the resulting anti-symmetric HOMO of the transition state.
Geometry of the transition state
| Bond | Optimised bond length (Å) | Typical/Theoretical bond length (Å) |
| C1-C4 | 1.397 | 1.52 |
| C1-C2 | 1.382 | 1.45 |
| C9-C12 | 1.383 | 1.45 |
| C2-C12§ | 2.119 | - |
§ - Note that this is not a real bond in the transition state, but rather a bond that will form in the process of forming the product; however observing this distance can give an indication as to how far the reaction has proceeded (i.e. this value will decrease as the reaction progresses, ultimately finishing at a value similar to a typical carbon-carbon single bond).
The above table illustrates that the optimised bond lengths are clearly shorter than the typical bond lengths expected. In addition, it can be seen that the bond lengths are all very similar and further comparison with the typical aromatic carbon-carbon bond length (1.38Å) allows the accurate deduction that the optimised transition state structure is very close to an aromatic structure. The reduced energy that arises as a result of the aromatic nature of the structure is essential in allowing the reaction to proceed (cf. single and double bonds with no delocalisation).
Regioselectivity - cyclohexa-1,3-diene and maleic anhydride
Optimisation of endo product
AM1-optimised endo product results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): -0.16017081 a.u. RMS Gradient Norm: 0.00002149 a.u. Imaginary Freq: 0 Dipole Moment: 5.5840 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 10.8 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000095 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.001207 0.001800 YES
RMS Displacement 0.000236 0.001200 YES
Predicted change in Energy=-4.132953D-08
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = -0.16017081 a.u.
Low frequencies --- -0.1992 -0.0942 -0.0034 2.0426 2.3852 2.9638 Low frequencies --- 72.2883 148.2752 167.5562
Optimisation of exo product
AM1-optimised exo product results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): -0.15990912 a.u. RMS Gradient Norm: 0.00007790 a.u. Imaginary Freq: 0 Dipole Moment: 5.2574 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 10.7 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000252 0.000450 YES
RMS Force 0.000038 0.000300 YES
Maximum Displacement 0.000855 0.001800 YES
RMS Displacement 0.000236 0.001200 YES
Predicted change in Energy=-2.971599D-07
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = -0.15990912 a.u.
Low frequencies --- -6.5865 -5.2281 -3.4452 -0.0027 0.0449 0.1118 Low frequencies --- 70.3927 148.3774 168.6296
Comparison of product structures
Upon comparison of the two product structures, the endo product is confirmed to be slightly lower in energy than the exo product. However the energy difference is so minimal (0.00026169 a.u.) that this cannot solely account for the significant preference of the endo vs. the exo product that is observed in this reaction. The reaction is known to proceed under kinetic control and thus the energies of the products will not be as significant; instead it is the relative energies of the two different transition states that must be investigated.
Optimisation of endo transition state
AM1-optimised endo TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): -0.05150480 a.u. RMS Gradient Norm: 0.00000456 a.u. Imaginary Freq: 1 Dipole Moment: 6.1664 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 10.8 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000216 0.001800 YES
RMS Displacement 0.000055 0.001200 YES
Predicted change in Energy=-1.506453D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = -0.05150480 a.u.
Low frequencies --- -806.4483 -1.5544 -0.9299 -0.3633 -0.0104 0.5214 Low frequencies --- 1.5807 62.4354 111.7372 ****** 1 imaginary frequencies (negative Signs) ******
The one imaginary frequency is observed at -806.4483 cm-1 and this vibration is animated below in order to confirm that it does indeed correspond to the Diels-Alder cycloaddition:
The animation illustrates that the bond formation in this reaction is a synchronous process and the presence of dotted-lined bonds implies that there is significant aromaticity within the transition state.
Optimisation of exo transition state
AM1-optimised exo TS results.
File Type: .log Calculation Type: FREQ Calculation Method: RAM1 Basis Set: ZDO Charge: 0 Spin: Singlet E(RAM1): -0.05041985 a.u. RMS Gradient Norm: 0.00000699 a.u. Imaginary Freq: 1 Dipole Moment: 5.5638 Debye Point Group: Cs Job CPU time: 0 days 0 hours 0 minutes 12.0 seconds.
The optimisation file (using the semi-empirical AM1 method) is linked to here.
Item Value Threshold Converged?
Maximum Force 0.000020 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000174 0.001800 YES
RMS Displacement 0.000030 0.001200 YES
Predicted change in Energy=-3.451335D-09
Optimization completed.
-- Stationary point found.
The Jmol for this optimisation given via this
Total energy for AM1 optimised structure = -0.05041985 a.u.
Low frequencies --- -812.1898 -1.3780 -1.1901 -0.0047 0.2799 1.0469 Low frequencies --- 2.2841 60.8620 123.8697 ****** 1 imaginary frequencies (negative Signs) ******
Again, one imaginary frequency is observed at -812.1898 cm-1 and this vibration is shown below, confirming that it does once again correspond to the Diels-Alder cycloaddition:
As with the case of the endo transition state, the exo transition state is shown to have significant aromatic character. The reaction via the exo product also involves the synchronous formation of the two new carbon-carbon bonds.
Comparison of transition state structures
Analysis of the relative energies of the transition states shows that the exo transition state is higher in energy than the endo transition state. It should be noted that the difference in these energies (0.00108495 a.u.) is more significant than the energy difference between the products (i.e. an order of magnitude greater). This is expected due to the fact that the reaction proceeds under kinetic control (i.e. the reaction is dependent on the height of the energy barrier within the potential energy surface); this helps to explain why the endo product is so significantly favoured over the exo product. To further understand this, there are two key explanations to support the endo product preference: steric effects and molecular orbital effects. The MOs of the two transition states were analysed subsequently in this work (see below) in order to highlight any potential MO effects. The steric effects involve the two hydrogens opposite the anhydride unit; in the exo TS these two hydrogens point directly towards the anhydride unit, whereas this is not the case in the endo TS. The net effect of this is that the distance between these two hydrogens and the anhydride unit is shorter in the exo TS compared to the endo TS, resulting in more steric repulsion hence raising the energy of the structure.
Comparison of transition state MOs
The images below illustrate the HOMOs for both the endo and exo transition states:
endo transition state HOMO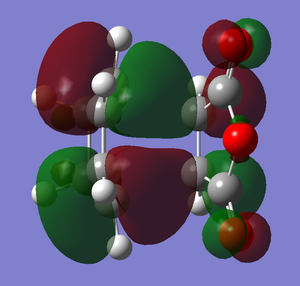 
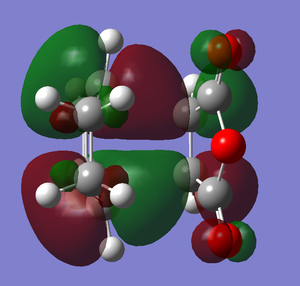exo transition state HOMO
Analysis of the transition state HOMOs produces interesting and perhaps unexpected observations. The transition state HOMOs formed in this reaction are analogous to that formed in the reaction between cis-butadiene and ethene, in the sense that anti-symmetric HOMOs have been formed from the anti-symmetric HOMO of the diene and the anti-symmetric LUMO of the dieneophile. Comparison of the two different HOMOs with each other (see above images) shows that in fact they are remarkably similar and almost identical in MO shape. This would ultimately suggest that the steric effects discussed earlier are far more major and significant in accounting for the difference in energy of the two reaction paths compared with the MO effects. The steric effects largely predominate over the orbital effects to explain the selectivity of this reaction.
Conclusion
Overall, this module has been highly effective in investigating the energetics of the Cope rearrangement and Diels-Alder cycloaddition reactions. Transition state structures have been successfully isolated and studied in order to identify various reaction pathways. In the example of the Cope rearrangement, it was successfully shown that the lowest energy reaction path proceeds via the "chair" conformation transition state due to its lower activation energy in comparison with the reaction path via the "boat" conformation. Studies of the Diels-Alder cycloaddition showed that the transition states for these reactions tend to resemble aromatic structures; in addition, the endo reaction pathway was shown to be lower in energy than the exo pathway and hence is the favoured product in these reactions. Further work could involve IRC analysis on the Diels-Alder cycloadditions to further investigate the reaction pathways and to obtain relative energy differences between the initial reactants and the final products; this would allow the determination as to whether changing the reaction pathway would affect this energy difference and whether there are any other effects to consider besides the steric and MO effects discussed in this work.