Rep:Mod:organictg1412
Conformational analysis using Molecular Mechanics
Molecular mechanics is a popular computational method often employed to investigate and calculate energies, carry out optimisations and examine different reactions and interactions, successfully, with large molecules, such as proteins, complex carbohydrates and medicinal drugs. These simulations use only classical mechanics, and avoid quantum mechanics, when simulating chemical and physical behaviours of molecular systems.
Force fields calculate the simulated molecule's interatomic potential energy. Force fields are vector fields which show the magnitude and direction of forces applied to molecular system in a particular configuration. The interatomic potential of molecular systems is calculated essentially by two parameters: the bonded energy and the non bonded energy. The bonded energy takes into account the energy of the bond, the energy of the the angle formed between two bonds and the dihedral energy (sum of the energies of angle bending and bond). These are energies associated with atoms that are covalently attached. The non covalent energy takes into account Van der Waals and electrostatic long range interactions between atoms. These equations are summarised in the equations below[20].
Ebonded = Edihedral + Ebond + Eangle
Enonbonded = EVan der Waals + Eelectrostatic
Molecular mechanics approach comes with pros and cons. MM, as mentioned already, can cope with very large molecules. However, you are required to know the specific atom and types for the entire molecule, and MM cannot cope with unusual bonding. MM provides accurate calculation results for systems which are near enough in structure to be able to emulate the force fields already calculated, thus having this interpolative property. However, the number of parameters required to accurately calculate structures increases very very fast when dealing with atoms which are not C, H, O or N. Therefore, using MM one must stay close to and cannot venture too far from already known chemistry.
This computational lab investigates the assortment of molecular modelling techniques to study various systems, namely, predictions of geometry, configurations and regioselectivity, prediction of 13C and 1H NMR and rationalisation of formations of molecules. Both MM and DFT (for NMR and optical rotation calculations) methods were used[21][22].
References
[20] https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:mechanics accessed 15/02/2015
[21] C. J. Casewit, K.S. Colwell, A. K. Rappe, J. Am. Chem. Soc., 1992, 114 (25), pp 10046–10053
[22] C. J. Casewit, K.S. Colwell, A. K. Rappe, J. Am. Chem. Soc., 1992, 114 (25), pp 10035–10046
The Hydrogenation of cyclopentadiene Dimer
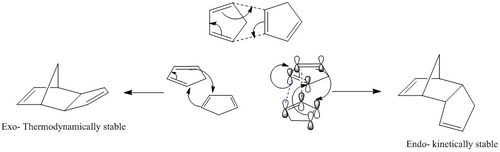
Cyclopentadiene can dimerise with itself in a 4+2 Diels Alder cycloadditon reaction to form the bicyclic dimer. The mechanism is shown in the picture below. There are two products which can form as a result of this dimerisation: the endo and the exo products. The Exo product is lower in energy, and is the thermodynamic product. Ie, height of the transition state barrier is not a determining factor in its formation. The endo product is a result of kinetic stability. Even though it is higher in energy, it is formed solely. This is because the formation of the endo dimer requires the crossing over a very low transition state barrier, along with additional secondary orbital overlaps between the two resulting alkene pi orbitals. This interaction provides additional stability for the dimer, regardless of the fact that it is still higher in energy.
 |
In this part of the exercise, the energies of the cyclopentadiene cyclodimerisations were calculated and analysed to see which dimers were thermodynamic and kinetic products.
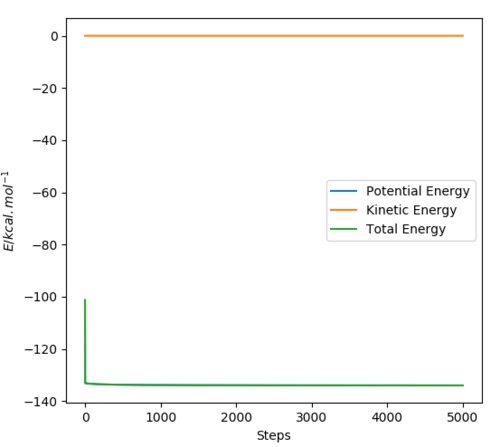
ChemBio3D was used to optimise the geometries of these dimers, using the MM2 method.
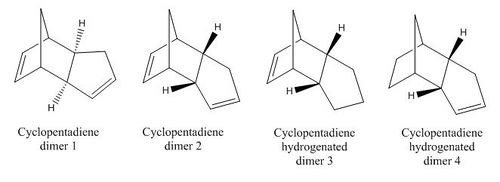
The cyclopentadiene dimer was drawn in ChemBio3D in both endo and exo conformations. The structures were then optimised to a minimum. The same was done for the hydrogenated dimers.
|
|
 |
| ||||
| Endo | Exo |
|
| ||||||||||||||||||||||||||||||||||||
 |
 |
| Reactant | Product |
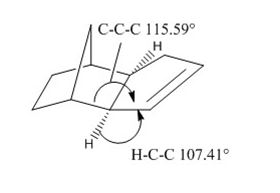
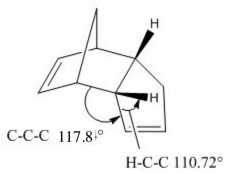
As can clearly be seen from these tables of dimer energies, dimer 1, the exo product, is 2.121 kcal/mol lower in energy than dimer 2, the endo product. Comparing the energy contributions of both dimer energies, the highest contribution to total energy is a result of the total angle bending energy. This energy is higher for the endo than the exo. Upon comparing the angles formed between the C-C-C bridges, the exo has shown a computed angle of 115.59, and endo a value of 117.80. The stable tetrahedral angle for sp3 hybridized carbon is 109.5, and with the endo having an angle larger, it is higher in energy. The exo product has an angle formed which is slightly smaller and closer to the desired 109.5 of sp3, so is less unstable. This forced and strained conformation of the endo dimer results in a H-C-C angle of 110.2. The torsional energies are also quite significant in these products. However, upon close inspection, the torsional energy of the endo product is higher than the exo. This is due to the larger deviation of ideal sp3 bond angle of the carbon atom involved in the bridging joint of the endo product. The higher energy of the endo product leads leads to the conclusion that this product is kinetically favoured.
|
| ||||||||||||||||||||||||||||||||||||
 |
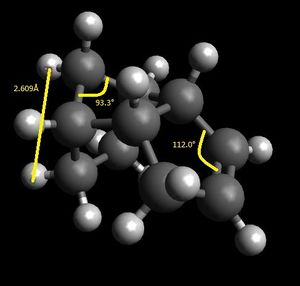 |
Dimers 3 and 4 are the products of hydrogenating dimer 2. Looking at the energy contributions, bending and torsional energies are the energies which contribute most to the total. Norbornene is a very strained molecule. It is a cyclohexene with a methylene bridge across the 1 and 3 carbons. The ideal sp3 angle, as mentioned already, is 109.5°. However, due to the forced and strained configuration of this bridge, the angle has been reduced to around 90°. For dimer 3, this angle is 93.7°, highly strained. Dimer 3 has an unsaturated part in the main cyclohexane ring. The ideal sp2 hybridized bond angle is 120°. The unsaturated carbons in dimer 3 has a bond angle of 107.4°, highly strained compared to the ideal 120°. Dimer 4 has the unsaturated carbons on the external 5 membered ring. This has an sp2 angle of 112.0°, still far from the ideal 120°, but closer than 107.4° of dimer 3. The methylene sp3 angle is 93.3°.
The highest contributing energies, once again, come from the total angle bending and torsional energies. Looking at the total energies of these two dimers, the dimer 4 has a lower energy to dimer 2 and dimer 3. Therefore, dimer 4 is the thermodynamic product in this hydrogenation.
Taxol is an important anti cancer drug used in chemotherapy for treatment of various different cancers[1]. Here, the atropisomerism of this molecule was investigated, and energies of different conformers were analysed and observed.
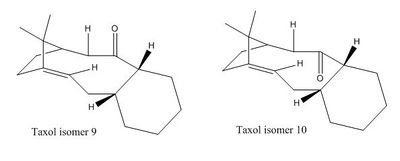
There are two intermediate molecules, which exists as two isomers, shown in the image opposite as isomers 9 and 10, which are used in the synthesis of taxol. It is synthesised with the carbonyl group pointing either up or down. When these two intermediates are left standing, one isomer will convert to another which is much more stable, via an isomerisation process. This geometry shift shows that the two structures differ in energy, and whether the carbonyl group is pointing up or down, the stereochemistry, plays an important role in thermodynamic stability of between the two[2].
'Atropisomerism' Atropisomerism is a phenomenon which arises from restricted rotation about one or more single bonds. This hindrance of rotation leads to stereoisomers of molecules, and most usually appears in macromolecules and macrocycles which have multiple single bonds and groups which require transition over large energy barriers in order to interconvert between the two stereoisomers. This high energy barrier for interconversion, thus, results in the isolation of two distinct isomers. Atropisomerism behaviour is displayed by isomers 9 and 10[2].
Upon contsructing the isomers, it was noted that the molecule contained a cyclohexane ring fused to a larger cyclic framework, essentially an extented norbornene structure. Cyclohexane can take up multiple conformations; chair, boat, twist chair and twist boat. For a free standing, unsubstituted cyclohexane ring, there exists two chair conformers, two twist chair conformers, two twist boat conformers and one boat conformer, and these mirrored conformers are the same in their energies. This taxol intermediate is asymmetric, therefore, the conformations which the cyclohexane in this molecule can take up will not be degenerate in their energies[3].
Shown below are four conformers of the taxol intermediate which were isolated using Avogadro and MMFF94s method. They are conformers in which the cyclohexane takes up the two chair and the two twist boat conformers. Only these conformers are isolable- they are low energy local minima on the energy profile diagram of cyclohexane conformers. The boat and twist chair could not be isolated as they are high energy maxima's, less stable and easily roll back to one of the structures which are low in energy and stable. Highlighted are the chair and twist boat structures for ease of identification.
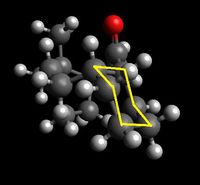 |
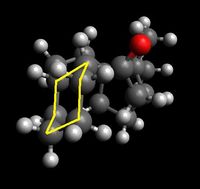 |
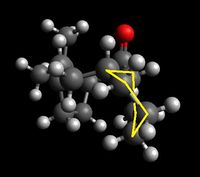 |
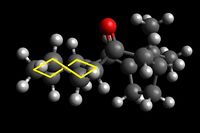 |
|
| ||||||||||||||||||||||||||||||||||||
| ' | ' |
|
| ||||||||||||||||||||||||||||||||||||
| ' | ' |
As can be seen from the tables of energies, each conformer has a different energy, and are not degenerate unlike with the case of the unsubstituted cyclohexane. It has been mentioned already that this is due to the fact that we are dealing with an asymmetric molecule, and this asymmetry removes the degeneracies. Much to our surprise, it seems as though there exists a twist boat conformer which is lower in energy than one of the chair conformers, namely twist boat 1 and chair 2 with energies 319.4 kJ/mol and 346.01 kJ/mol respectively.
For each of these isomers, the largest energy contributions come from the total bending and the total Van der Waals energies. The Van der Waals energies are high for these molecules- they are crowded, and sterically strained due to their fused cyclic natures. The hydrogen and methyl groups are forced into close proximity, and many atoms and bonds are close together which all raise the energies of the molecules. Being sterically strained and having many bonds involved in cyclic structures causes the angle bending energies to be high too. In order to invert the angles generated between two bonds, the structure will need to undergo geometric changes. The higher energy conformers have larger angle bending energies, which reflects on their configurations being unfavourable, thus not found in high enough quantities in equilibrium at room temperature.
 |
 |
 |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ' | ' |
Shown above are the different energy conformers of isomer 10. Here, only three conformers were able to be isolated: the two chair and twist boat. The corresponding twist boat could not be isolated using Avogadro, as its energy was far too high, resulting in an unstable conformer which would simply roll down to a potential energy minimum; either the chair or the stable twist boat. As with conformations for isomer 9, the Van der Waals and bending energies are the energies contributing most to the total energies of each isomer. Chair 1 has been calculated to be the most stable conformer. Isomers 9 and 10 are atropisomers. Isomer 9 can take up four structures which can be isolated using computational methods, whereas isomer 10, only three were found. The range of energies which isomer 9 can take up spans between 295.33 - 369.09 kJ/mol, and for isomer 10; 253.52 - 312.88 kJ/mol. Since isomer 10 has a range spanning smaller energies, it can be accepted that isomer 10 is the lower energy atropisomer. Both chair and twist boat conformers are lower in energy than the corresponding chair and twist boat conformer energies found in isomer 9.
Hyperstable Alkenes
Hyperstable alkenes are alkenes found in bridge heads which, counterintuitively, are lower in energy than their parent hydrocarbon. The table above shows energies related to the parent hydrocarbon of isomer 10 twist boat, and as you can see, its energy is higher by approximately 38kJ/mol. Most of the contributing energy comes from the bending and torsional energies, due to presence of a single bond with H atoms which provide extra resistance upon rotations and turning[4][5].
References
[1] K. C. NICOLAOU, Z. YANG, J. J. LIU, H. UENO, P. G. NANTERMET, R. K. GUY, C. F. CLAIBORNE, J. RENAUD, E. A. COULADOUROS, K. PAULVANNAN E. J. SORENSEN, Nature 367, 630 - 634
[2] http://www.ch.imperial.ac.uk/rzepa/blog/?p=5345, accessed 14/02/2-15
[3] D. G. Shaw, J. Chem. Educ., 1988, 65 (7), p 587
[4] R. A. Moss, Reactive intermediates, 2004, John Wiley & Sons
[5] W. F. Maier J. Am. Chem. Soc., Vol. 103, No. 8, 1981
Spectroscopic Simulation using Quantum Mechanics
Taking the lowest energy conformers, a DFT calculation (Basis set B3LYP/6-31G(d,p)) was carried out in order to compute the 1H and 13C NMRs of each. The discussion which follows analyses the integrity of simulated NMRs against literature values.
Isomer 17 Chair 1
DOI:10042/193908 log file
|
|
 | ||
| Isomer 17, Chair1 | Isomer 17, Chair1 |
|
| ||||||||||||||||||||||||||||
The largest energy contributions come from total Van der Waals and total bending energies. The total Van der Waals energy takes into account attractive and repulsive interatomic forces between non bonded atoms. This value is significant in this molecule due to lots of H atoms flanking groups such as O. Also, they are forced into close proximity due to the multiple ring structures fused together. It is a sterically strained ring molecule. All these factors raise the energy of the molecules, thus has the largest contribution in the total energy. This selected chair conformer of isomer 17 is 57.249kcal/mol lower in energy than the mirroring chair conformer (not shown). It therefore follows that the higher energy chair conformer has a higher total VdW energy when compared to this lower energy chair conformer of isomer 17, 0.372kcal/mol higher to be exact. Another reason why steric strain is lower for this chair conformer could be due to the carbon atoms being on the opposite side to the methyl group. Being further away from the methyl group reduces steric crowdedness and keeps energy low. This is shown in the diagram below
 |
The bending energy of these molecules are potential energies bending between two bonds. The more strained or the more stiffer the bonds which are bending, the higher the potential energy. These values for bending energies are also particularly large for these molecules. As mentioned before, multiple bonding and fused ring systems are sterically strained, so it follows that bending energy should be high. When comparing this lower energy chair conformer with its higher energy mirror chair conformer, it was found that the total bending energy of the higher energy conformer of isomer 17 was 39.59469 kcal/mol, a huge 8.74119kcal/mol difference. These comparisons of bending energy may go to show why interconversion between these two chair conformers for isomer 17 will not be rapid- bond angles will need to bend in order to pass the high energy transition states when converting from one chair to another, and the potential energy for the higher energy chair conformer is very high to be facile at room temperature.
The free energy of the molecules is given by the Σ Electronic & Thermal free energies, which is equivalent to G=H-TS. For the two chair conformers for isomer 17, the free energies are -1651.460 Hartrees and -1612.154172 Hartrees, low energy and high energy chair conformers respectively. The higher energy chair conformer for isomer 17 has a higher value for the free energy compared to the lower energy chair conformation which is shown and discussed. This fits the idea that the high energy conformer is less stable. A similar analysis can be make for the two twist boat conformers of isomer 17. however, since they were calculated to be too high in energy, along with the higher energy chair conformer, they have not been included in this wiki and NMR analysis has been left out.
Isomer 18 chair and twist boat conformers have free energies -1651.4630 Hartrees and -1651.4628 Hartrees respectively. These energies are very close to each other, and it follows that these conformers are fairly stable. The corresponding higher energy chair total energies was calculated to be 441.807kJ/mol. This energy is too high, and results in an unstable conformer. For this reason, subsequent NMR analysis has been left out for this configuration, as you wouldnt be able to find a good amount of it in equilibrium at room temperature. The corresponding high energy twist boat was too high in energy to locate (~350 kJ/mol), so kept minimising to either the low energy chair or twist boat. Hence, it has been left out of the analysis which follows.
'Discussion of 1H NMR'
 |
| Isomer 17, Chair1 1H NMR |
| |||||||||||||||||||||||||||||||
Above are all data belonging to the chair conformer found of isomer 17.
As can be seen from the table showing all 1H NMR chemical shifts, the calculated chemical shifts are fairly comparable to those found in literature[6]. The shift at 5.23 is characteristic of an allylic proton. It is fairly deshielded due to the anisotropy of double bonds[CITATION NEEDED]- there is a region which is deshielded which can be found along the plane of the C=C bond. It is in acceptable agreement with the shift value found in literature (4.88) though not perfect. Literature says a dd multiplicity is observed. This can be attributed to proton 15 being adjacent to a set of methylene protons (41 & 42) which are diastereotopic due to being adjacent to a chiral centre (C14). Since H's 41 and 42 are inequivalent, they would be in two different environments, thus splitting the H15 peak into a dd.
H 21 is also a singlet. Following the same argument, it is adjacent to a pair of unsymmetrical H's, 41 and 42, thus showing a dd splitting as mentioned by the literature. It is very good agreement with reported chemical shift, 3.08 compared to reported 2.99
Since H 41 is diastereotopic with its geminal H, this is expected to show a multiplet- a ddd (due to coupling with H21, H15 and H42). This can be nicely matched with what is reported in literature, where a multiplet is assigned with a calculated shift of 2.52. This value, however, is not in good agreement with literature (1.00-0.80).
There is a complicated region of alkyl protons. These can be assigned to the 14H mentioned in the literature, and calculated values are within the range of values given in literature.
The methyl H shifts which are observed are the average of the 3 protons. The larger of the three average shifts have been assigned to protons 51, 52, 53. I expect these to be higher than the remaining two sets of methyl protons, as it in in close proximity to an electron withdrawing carbonyl group. However, the match with literature (1.38, the most deshielded value for methyl proton sets in literature) is poor. the remaining two sets of methyl proton shifts are in somewhat acceptable agreement with literature.
Protons 43, 44, 45 and 46 can be assigned the calculated chemical shift values specified in the table above. These are in good agreement with literature and integration also matches.
'Discussion of 13C NMR'
 |
| Isomer 17, Chair1 13C NMR |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The table above compares 13C NMR calculated shifts and shifts reported in literature. Calculated values are in very good agreement to literature values.
Suggestions for the discrepancies between calculated and reported shifts can be explained by analysing the methods we used in this computational exercise. Firstly, the calculated outcomes are only a result of simulations, which do not take into account many factors which exist in experiment. Therefore, all results obtained are due to proposed models, electronic and potential energies. The corresponding synthesis experiment will have many other factors such as temperature and pressure deviations and solvent purity playing a part, thus deviating calculated results from the true natural values. This is also something which occurs in general computational experiments.
Another factor which will provide different results is the solvent choice. The literature uses deuterated benzene as solvent, whereas the calculations used simply chloroform. Having this change in solvent will not affect splitting of peaks, but will affect the chemical shift at which the peaks are observed.
Also, when choosing a TMS reference for NMR in Gaussian, the basis set used, TMS B3LYP/6-311+G(2d,p) GIAO, does not fully match the basis set 6-31G(d,p) used in calculations. This is an obvious source of discrepancy in results obtained.
The tables below show the deviations of calculated shifts against literature reported shifts.
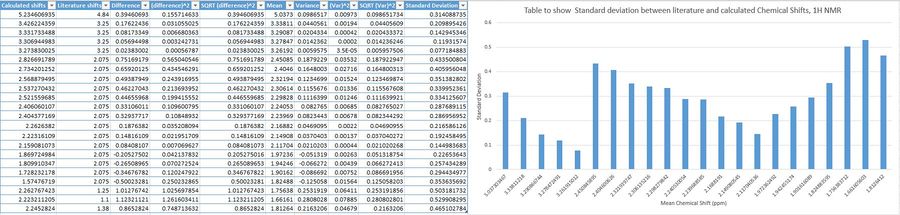 | |
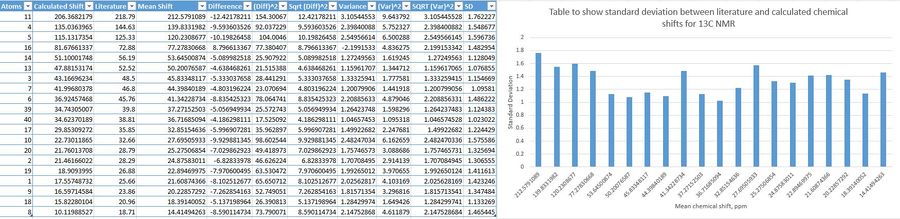 | |
The bar graphs show fairly substantial deviations- the bars are high. There is more discrepancy for shifts in the proton NMR- there is lots of variations by how much values change from the mean. Whereas for 13C NMR, the disparity is fairly constant, but high. This could be due to sensitivity differences for 1H and 13C NMR calculations, intrinsic to the computational method. The largest difference in chemical shifts for 1H NMR between calculated and literature values was 1.12ppm, and for 13C, 12.42ppm. These differences are fairly large. Attempts at providing absolute atom assignments were made, however, it is difficult to say for sure which 1H or 13C belonged to which chemical shift value, so simulating NMRs with certain shift assignment for complex molecules is very difficult.
Isomer 18, Chair 1
The same procedures of running 13C and 1H NMRs for the chair and twist boat conformations of isomer 18 were carried out. One particular chair and twist boat were selected due to having the lowest energy conformations with a very small energy difference between them (twist boat ~10kJ/mol higher than corresponding chair). The data is provided and explained below.
DOI:10042/193914 log file
|
|
 | ||
| Isomer 18, Chair1 | Isomer 18, Chair1 |
|
| ||||||||||||||||||||||||||||
Once again, the energy contributions to the total energy of this conformer is largely swamped by the total Van der Waals and total bending energies. The argument follows as with the chair conformer for isomer 17 above.
 |
| Isomer 17, Chair1 13C NMR |
| ||||||||||||||||||||||||||||||||||
Similar analysis can be made with the 1H NMR of this isomer as was made with isomer 17 above. These 1H NMR calculated shifts, though reasonably similar to literature values, still have significant differences. The easiest proton which can be identified is the allyl H, at 6.11ppm, and this proton can be most easily assigned to the literature value chemical shift of 5.21ppm. A fairly significant difference can once again be attributed to the difference of use of solvent: paper being refernced to utilises deuterated benzene, whereas in these DFT calculations, we used chloroform. These variations are best shown in the bar graph below, which shows significant differences between reported and calculated shifts between each assigned atom.
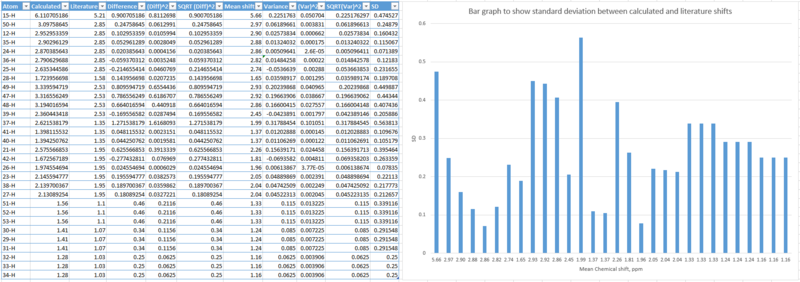 |
The standard deviations of the chemical shifts calculated, compared to literature values varies quite a lot, as can be seen from the erratic fluctuations in the heights of the bars in the figure above. The largest chemical shift difference found was 10.47ppm. Such large differences between calculated and reported shifts leave space for immense uncertainty in accuracy of simulated NMRs.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Comparison of the calculated chemical shifts for 13C NMR against those found in literature show acceptable agreement, though still very different from the true reported values. The largest difference between shifts was of a value of 10.35ppm, which is quite high. Carbon 11 is bonded to an oxygen atom, so gibes the largest chemical shift. This value is around 10ppm lower than the reported value for the shift. Once again, these discrepancies can be blamed on use of different solvent in the simulation, incorrect basis set approximation and sensitivity in geometry.
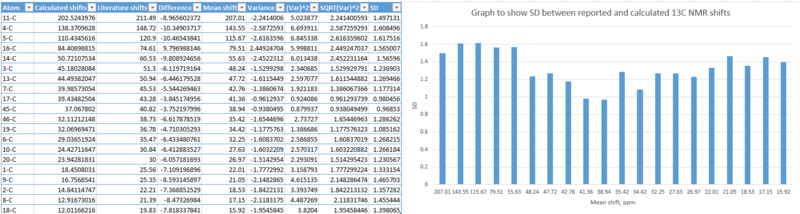 |
The bar graph of standard deviation above, between calculated and reported 13C NMR chemical shifts is reported. It shows a fairly constant deviation across all carbon atom shifts, unlike with the 1H NMR which showed very aggravated variations in bar heights. Even with similar magnitude of deviations, the differences between calculated and reported shifts are still substantial, and provides room for uncertainty in the accuracy of the NMRs which have been simulated. From the simulated 1H NMRs above, it seems that 1H NMRs are most sensitive to changes in chemical shifts since the calculated differences vary dramatically from literature values.
Isomer 18, Twist boat 1
|
|
 | ||
| Isomer 18, Twist boat1 | Isomer 18, Twist boat1 |
|
| ||||||||||||||||||||||||||||
Literature values could not be found for twist boat conformation. However, given that the energies between this twist boat and the chair for isomer 18 are very close in energy, I would expect both of these conformers to be present in equilibrium, and I would expect the NMRs for each of these to be a superposition of the two. Calculated equilibrium constants for the conversion of the chair conformer to the twist boat was found to be 1.00023, using the equation k = exp(-ΔG/RT) from ΔG = -RTlnk. In a similar way, the equilibrium constant for the conversion from twist boat conformer to the chair was found to be 0.99977. These equilibrium constants are extremely close and almost identical. This supports the idea that they are fluctional in ambient conditions, and we are expected to observe both at equilibrium.
This could be a reason as to why it proved difficult to assign NMR data for this isomer. Since this isomer has two conformers which are readily fluctuating, the reported literature values for this isomer may contain peaks which are undefined as a result of an overlap of two NMRs, for each conformer.
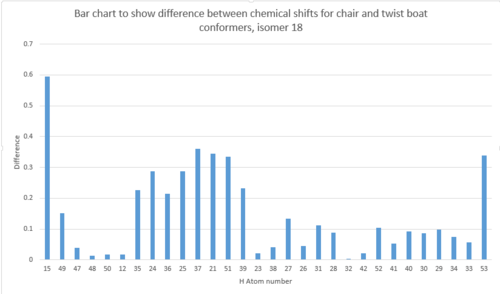 | |
Above is a graph displaying the difference in chemical shifts for 1H NMR for isomer 18 chair and twist boats. Even though it seems that there is lots of variation, the actual standard deviation values are very small, all within 0.6, and this shows that the two produce chemical shift values which are not too dissimilar, thus strengthening the argument that the two conformers are readily fluctuating and swapping between the two.
References
[6] L. A. Paquette, N. A. Pegg, J. Am. Chem. Soc., 1990, 112 (1), pp 277–283
Analysis of the properties of the synthesised alkene epoxides
The Shi and Jacobsen asymmetric epoxidation catalysts are used for the sythesis of epoxides from alkenes of different natures. Below, I will describe procedures and calculations carried out to generate two epoxides from two alkenes, namely 1,2-dihydronaphthalene and trans-Stilbene, and will also discuss their physical and geometric properties.
Two catalytic systems
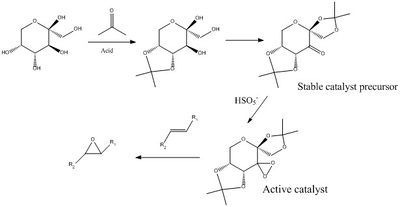
Shi fructose-derived chiral catalyst
The Shi catalyst is derived from D-fructose[7]. It provides very high enantiomeric excesses, when compared to metal catalysts used for epoxidations of alkenes. Below is a mechanistic scheme of the synthesis of the stable catalyst (ketone bearing moiety) and the active catalyst- activated upon addition of persulphuric acid.
 |
|
The Shi catalyst was drawn using Avogadro and optimised using MMFF94s method. The structure is composed of a tetra substituted pyran ring. This ring takes up a low energy chair conformation. The anomeric effect is a stereoelectronic effect which explains why electron withdrawing groups in a cyclohexane ring such as tetra substituted pyran, whilst adjacent to the heteroatom of the ring, prefers to take up the axial position. This phenomenon is shown diagramatically in the picture below. The lone pair of electrond in the oxygen atom of the ring is able to donate electrons into the antiperiplanar C-O sigma* antibonding orbital. This provides a "pseudo double bond- no bond" structure. Therefore, calculated bond lengths should show significant bond lengthening and shortening, due to this anomeric effect[8].
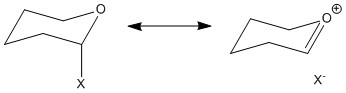
|
|
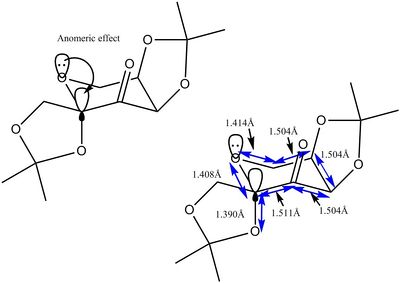 |
 | ||
The figure above displays the bond distances. There is a significant bond shortening of C-O in ring, length of 1.408Å. The average bond length of C-O is 1.43Å[9]. This shortening is consistent with the anomeric effect, where the bond order increases, thus shrinking the length between the C and the O atom. However, the axial C-O bond length is 1.39Å. This is of course shorter than the C-O ideal bond length, whereas the anomeric effect suggests it should be longer. This could be due to the axial group being sterically contrained within a ring system, so is unable to extend in length by much.
Anomeric effect exists.
Significant bond shortening of ring C-O- 1.42415A due to lone pair donation into sigma* of C-O axial.
"No bond-double bond" structure.
would expect axial C-O bond to be longer than 1.43A (bond length of C-O) but is less- 1.42670A maybe shorter due to ring strain?
The Jacobsen salen-derived chiral catalyst
The Jacobsen salen derived catalyst is also another asymmetric catalyst used in the epoxidation of several different alkenes. It has very high enantioselectivity towards prochiral alkenes, and can transform them into epoxides. It's structure is composed of metal Manganese centre of high valency, and is surrounded in an almost 'cage' type structure surrounded by nitrogen and oxygen atoms. The carbon ring system which encapsulates the Mn metal is the ligand, and is tetra-dentate. The alkenes which the Jacobsen catalyst can most well epoxidize are unsubstituted aryl and/or alkyl alkenes[10].
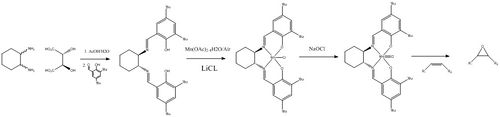 |
|
Below is a 3D visualisation of the catalyst, and a crystal structure showing bond lengths and angles. These will be discussed below.
|
|
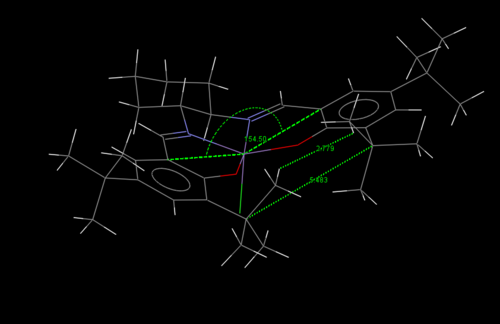 |
|||
As can be seen, this is a very crowded molecule. Upon close inspection, it can be seen that this molecule is not planar. It is slightly bent, with both ring structures bending upwards slightly. This creates an angle across the molecule of 154.50°. Looking at the molecule along its centre, you can see that the ring furthest at the back isnt planar, but twisted. Also, the tertiary butyl groups are very bulky on the periphery of the rings are very bulky and sterically demanding. There are two tertiary butyl groups which approach each other fairly closely from opposite rings. This close approach is sterically hindered, and there exists much repulsive forces between the two. To relieve the stress, it can be suggested that the two tBu groups are off set, so are not facing each other directly. This twist generates an axis of chirality along the molecule, and this could be where the asymmetry and chirality arise for this catalyst.
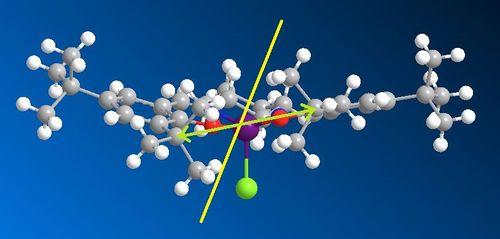 |
|
References
[7] D. Weibel, Aldrich ChemFiles' 2010, 10.3, 5
[8] F. Grein, . Deslongchamps, Can. J. Chem, 1992, 70, 1562
[9] http://iqscience.richmond.edu/resources/materials/Geometries.pdf, accessed 14/02/2015
[10] W. Zhang, J. L. Loebach, S. R. Wilson, E. N. Jacobsen, Journal of the American Chemical Society, 1990, 112 (7): 2801–2803.
Assigning the absolute configuration of the product
The absolute configuration of the computed epoxides were determined using DFT. [TALK ABOUT OPTICAL ROTATIONS]
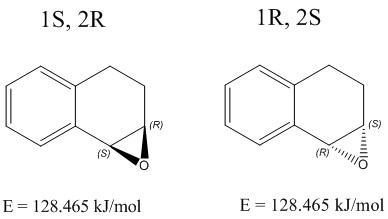
1,2-Dihydronaphthalene
SR DOI:10042/193907
RS
|
|
 |
| ||||
| Optical rotation computed: -155.82° | Optical rotation computed: +156.05° |
The epoxides were drawn using Avogadro, and optimised using the MMFF94s method. This file was then optimised using DFT, and the resulting output file was resubmitted and re-subjected to DFT calculations in order to obtain the optical rotation values at 589nm and 365nm.
The calculated value obtained for the 1S,2R enantiomer of the epoxide of 1,2-dihydronaphthalene was -155.82°. Literature values show the reported optical rotation to be -144.9°[11], at 539nm. The calculated value seems to be out with an error of 7.54%. The 1R,2S enantiomer is presumed to be same in magnitude to the 1S,2R, but with opposite sign. However, the separately computed optical rotation value for the 1R,2S enantiomer does not seem to be identical, with a value of 156.05°. Optical rotation calculations are highly sensitive. They are extremely sensitive to any change in geometry and structure, as changes to this would submit a structure with a different energy value, even if only marginely small. Even though the energies of the two enantiomers which I drew were the same, the calculated output value for the optical rotations still seem to differ. Also, the calculations used chloroform solvent, whereas the literature being referenced to used deuterated chloroform as solvent. Optical rotations are highly sensitive to solvent choice, temperature, and purity, and these could all be factors which deviate the calculated optical rotation from the reported values[11].
1H NMR
The table below shows the 1H NMR data calculated, and comparisons have been made with literature.
| |||||||||||||||||||||||||||||||||||||
There are four protons which have chemical shifts characteristic of being part of an aromatic ring system. The difference between calculated and reported chemical shifts for this proton is 0.2263ppm. Proton 14 has been assigned the highest chemical shift, due to its close proximity to the epoxide. Protons 16 and 17 have quite high chemical shifts, characteristic of C-O bonds. Protons 18 and 19 have been calculated to have different chemical shifts, due to being adjacent to carbon atom 8, which is a chiral centre, hence are diastereotopic protons. Overall, the protons can be assigned with literature values fairly easily.
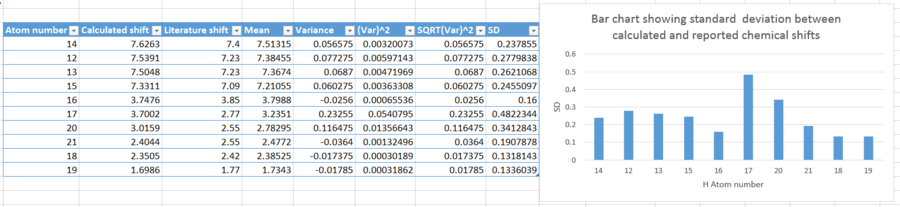 | |
The graph above displays the standard deviation in chemical shift between calculated and reported literature values. Proton 17 has the highest deviation, a difference of chemical shift of 0.9302. This is fairly substantial, and gives rise to uncertainty and far deviation from true value. Once again, these differences can be attributed to use of different solvent, and use of different temperature in calculations compared to literature.
13C NMR
The chart below shows and compares calculated chemical shift values and compares them against literature reported values.
| |||||||||||||||||||||||||||||||||||||
The calculated chemical shifts are of the order of what I would expect, carbon atoms 4 and 5 being most deshielded due to its position in the aromatic ring structure. All C atoms involved in the aromatic ring, atoms 6, 1, 3 and 2, are all around the expected aromatic carbon chemical shifts.
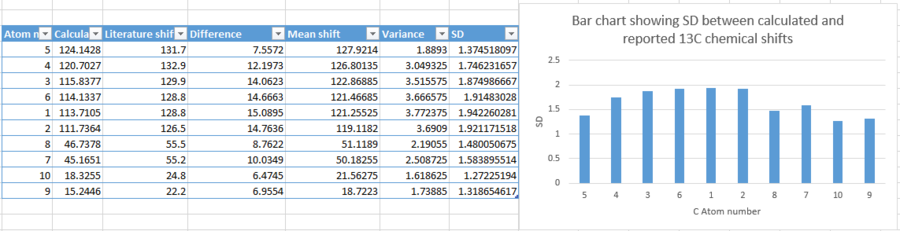 | |
Even though the standard deviation between calculated and reported shifts are fairly constant in bar height, the actual value of the deviation is incredibly high. the largest difference between chemical shifts has been found to be 15.0895ppm, and a standard deviation of approximately 1.94. This provides huge discrepancy between calculated and reported shifts, thus being an unreliable method to simulate the NMR. Though, it must be taken into account that solvent, temperature and basis set are all varying between calculations and between calculated chemical shift and those reported in literature, thus provided potential sources for the inaccuracy.
Trans-Stilbene
DOI:10042/193909 RR DOI:10042/193910 SS
|
|
 |
| ||||
| Optical rotation computed: +297.87° | Optical rotation computed: -297.85° |
The same procedure was carried out for the trans Stilbene alkene. DFT calculations returned an optical rotation value of +297.87° for the R,R-enantiomer, and a value of -297.82° for the corresponding S,S-enantiomer. Literature values report an optical rotation of -249° [13]at 589nm. However, this reported literature value, though carried out in chloroform solvent, was also carried out at a temperature of 15°C. Calculations are carried out at 298.15K, so this, along with the fact that the concentration of the alkene in the literature was 0.5, different to calculated concentration, prove to be reasons for the discrepancy between calculated and reported values.
1H NMR
The table below shows the 1H NMR data calculated, and comparisons have been made with literature.
| |||||||||||||||||||||||||||||||||||||||||||
There are four protons which have chemical shifts characteristic of being part of an aromatic ring system. The difference between calculated and reported chemical shifts for this proton is 0.2263ppm. Proton 14 has been assigned the highest chemical shift, due to its close proximity to the epoxide. Protons 16 and 17 have quite high chemical shifts, characteristic of C-O bonds. Protons 18 and 19 have been calculated to have different chemical shifts, due to being adjacent to carbon atom 8, which is a chiral centre, hence are diastereotopic protons. Overall, the protons can be assigned with literature values fairly easily.
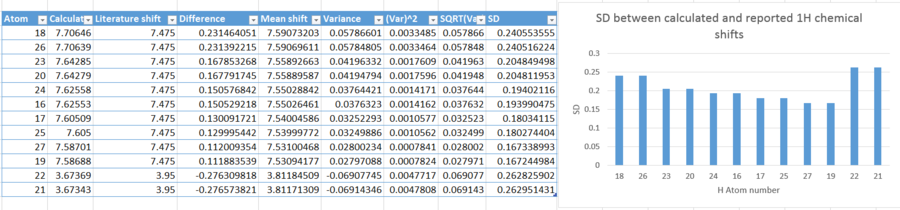 | |
The graph above displays the standard deviation in chemical shift between calculated and reported literature values. Proton 17 has the highest deviation, a difference of chemical shift of 0.9302. This is fairly substantial, and gives rise to uncertainty and far deviation from true value. Once again, these differences can be attributed to use of different solvent, and use of different temperature in calculations compared to literature.
13C
| |||||||||||||||||||||||||||||||||||||||||||
The calculated chemical shifts have correctly identified chemical shifts relating to the 12 aromatic carbons. The two carbons bridging the two phenyl groups have also been identified and calculated to have a chemical shift around the general region of shifts you would expect to find for a carbon bonded to a phenyl group. However, the discrepancy between the calculated and reported shifts are quite high. This is discussed below.
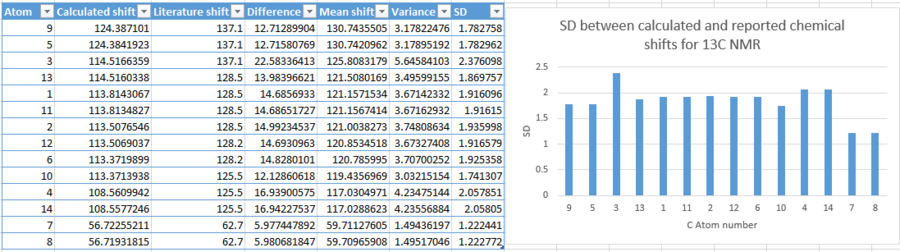 | |
This graph of standard deviation between calculated and reported chemical shifts shows very high discrepancies between the two. The highest value of deviation has been calculated as 2.376. This is a huge difference, and such a deviation from literature value renders the simulation technique for 13C NMR calculations redundant. It is a very unreliable method, even though it is shows by the graph that the deviations, though high, are fairly constant, shown by similar heights of the bars.
References
[11] H. Sasaki, R. Irie, K. Suzuki, T. Katsuki, Tetrahedron, 1994, 50(41)
[12] D. J. Phillips, J. L. Kean, A. E. Graham, Tetrahedron, 2013, 69, 6196-6202
[13] J. Read, I. G. M. Campbell, J. Chem. Soc., 1930, 2377-2384
Using the (calculated) properties of transition state for the reaction
Provided to us were the transition state energies of our chosen alkenes, en route to a particular enantiomer. The free energies were taken from the DFT calculated .log files, in order to obtain thermochemistry data- the sum of electronic and free energies in particular. These transition state energies were provided to us for both Shi and Jacobsen catalysts. There are many different local minima of the transition state geometries, a few are given in the tables below for each catalyst. The lowest (thus most stable) energies were selected for subsequent calculations.
Shi catalyst
| Free energy of RR TS, kJ/mol | Free energy of SS TS, kJ/mol |
|---|---|
| -4029323.146842 | -4029311.678657 |
| -4029321.687063 | -4029316.008107 |
| -4029355.254084 low | -4029338.926098 low |
| -4029354.8970155 | -4029333.780117 |
Enantiomeric excess is calculated using the equation ee = (exp(-ΔG/RT)-1) / (exp(-ΔG/RT)+1). Taking the lowest energies for each diastereomeric transition state, between each epoxide enantiomer, the free energy between these transition states, ΔG, was calculated. This is the value given by the difference between the free energy values. ΔG = G(favoured) - G(disfavoured)
For Trans Stilbene, taking the lowest free energy value by calculating R,R series - S,S series, ΔG = -16.327986 kJ/mol. Plugging this into the equation above gives an ee (SS/RR) = 3.2934 x 10^-3. This is the ratio of the SS enantiomer formed/present in solution to the RR enantiomer. The ratio of RR enantiomer to SS is thus 1 - 3.2934 x 10^-3 = 0.996706511. Clearly, this shows that the RR enantiomer formation of trans Stilbene oxide is favoured greatly over the SS trans Stilbene oxide, therefore more is present in solution. This is because, even though the starting materials and final epoxide enantiomer products are the same in energies, the transition energy barrier can differ for each enantiomer, and is lower for the RR enantiomer [INSERT DIAGRAM]. This is in excellent agreement with literature value[14] of 99%
| Free energy of RS TS, kJ/mol | Free energy of SR TS, kJ/mol |
|---|---|
| -3626132.889365 | -3626160.617273 |
| -3626146.289918 | -3626120.620403 |
| -3626167.748131 | -3626146.69162 |
| -3626148.484836 | -3626173.471722 |
Once again, taking the lowest energies from each diastereotopic transition state of each epoxide enantiomer, ΔG = -5.723591 kJ/mol, for R,S - S,R. When plugged into the equation above, an enantiomeric excess value of 1.15 x 10^-3 was found. This is the value of ee of the ratio R,S/S,R. 1 - 1.15 x 10^-3 provides the ee value of 0.9988 for formation of S,R. Since the free energy value for the transition state barrier en route to the S,R enantiomer is lower than that for R,S, this proves that more of the S,R enantiomer is made. This is in good agreement with literature value[15] of 97%
Jacobsen
| Free energy of RR TS, kJ/mol | Free energy of SS TS, kJ/mol |
|---|---|
| -9385961.279903 | -9385956.257321 |
Using the Jacobsen catalyst now, and going from enatiomer R,R to S,S, a free energy of ΔG = -5.022582 kJ/mol was found. ee = 1.0131 x 10^-3. This ratio value for S,S/R,R is very small, and shows that the S,S enantiomer of the epoxide is disfavoured, due to high transition state energy, with a barrier very difficult to cross. Therefore, less of the S,S enantiomer is found in solution at equilibrium. The R,R enantiomer has a ratio R,R/S,S of 0.99899, showing favourable epoxide formation. Literature[14] reports an ee% value of RR of 97%. This is extremely close to calculated value, however, the structure during calculation is extremely sensitive to solvents, geometry, perturbations, temperature and concentration. The literature used a solvent of benzene. This is a point of discrepancy.
| Free energy of RS TS, kJ/mol | Free energy of SR TS, kJ/mol |
|---|---|
| -8982805.080415 low | -8982779.668199 low |
| -8982785.512562 | -8982718.2207296 |
The epoxidation of Dihydronaphthalene using the Jacobsen catalyst gives ΔG = -25.412216kJ/mol. This is the free energy value obtained when taking away the R,S transition state free energy from the S,R transition state free energy. This provides us with an enantiomeric excess ratio for S,R/R,S = 5.126 x 10^-3. The enantiomeric excess for the R,S enantiomer is thus 1 - 5.126 x 10^-3 = 0.995. Thus, formation of R,S enantiomer is favoured, as it requires a low barrier crossing over its transition state. According to reference 11, it seems as though the S,R enantiomer has been experimentally observed to have a higher enantiomeric ratio than R,S. This raises a point of uncertainty and unreliability in DFT calculations to compute an absolute enantiomeric excess value of this molecule.
References
[14] O. A. Wong, B. Wang, J. Org. Chem, 2009, 74 (16), p6335–6338
[15] D. Xiong, X. Hu, S. Wang, C. Miao, W. Sun, Eur. J. of Org. Chem., 2011, (2011)
Investigating the non-covalent interactions in the active-site of the reaction transition state
Non covalent interactions are interactions between atoms which occur through space. They involve interactions such as Van der Waals, Hydrophobic, electrostatic and pi-pi orbital interactions. They do not involve the sharing of electrons, but are responsible for the quaternary and three dimensional structures of macromolecules and proteins. These interactions provide stability to the molecule[16].
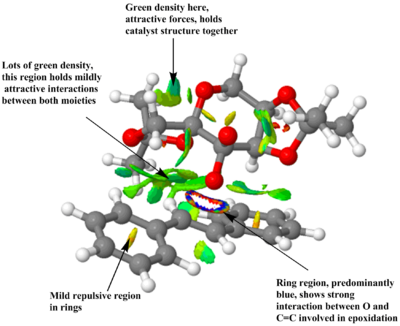
Using the transition structure of the epoxidation reaction between (R,R)trans-Stilbene and Shi catalyst, an NCI analysis was carried out in order to examine the favourable and disfavourable communications between atoms and groups of atoms at this transition state. Taking the precalculated files from the data repository provided, the following structures were resulted.
 |
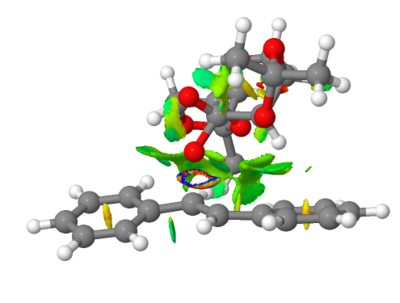 |
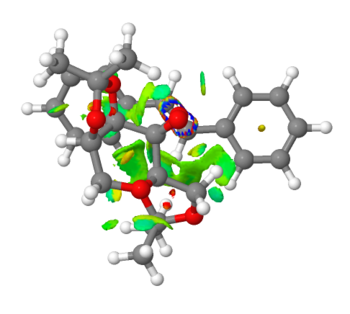 |
Coloured places on the interatomic surfaces are the Reduced Density Gradients, coloured according to the value of the second eigenvalue of the Hessian matrix relating to the electron density at that point. Regions of blue density show strongly stabilising attractive interactions between groups of atoms. Regions of green density show mildly attractive Van der Waals interactions between groups. Yellow density show areas in which interactions are mildly repulsive, and red shows strongly repulsive interactions in that space between those groups. Repulsive regions are shown in the centre of the cyclic ring systems. This is due to the hydrogen atoms creating a shielded space in the centre with high electron density. As can be seen from these pictures, there exists a lot of green density between the two structures, as they come together at the transition state. This shows that there exists lots of favourable attractive forces which help the two structures approach closely, thus enabling epoxidation reaction to occur. There is a particular region where one finds very strong stabilising density, an almost 'ring' type region between the O atom of the catalyst and the C=C fragment of the alkene. This shows strong interactions between the atoms involved in the epoxidation of this trans Stilbene and the Shi catalyst. These interactions demonstrate the feasibility of reaction with respect to atoms involved in reaction[17].
References
[16] L. S. Cockroft, C. A. Hunter, Chemical Society Reviews, 2007, 36 (2), 172
[17] http://www.ncbi.nlm.nih.gov/books/NBK21726/ accessed 14/02/2015
Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state
A bond can be considered as electron density concentration along a line which connects two nuclei. The Bond Critical Point is a point in space along this hypothetical 'line' which connects the two nuclei, where the derivative of electron density which is being shared between the two atoms reaches zero, in other words, a minimum. This electron density is located in the bonding regions between two nuclei. These bond critical points are identified in the pictures below as a yellow sphere between two atoms, both intermolecular and intramolecular[18][19].
 | |
Above is the transition structure for the formation of R,S enantiomer of 1,2-dihydronaphthalene, using Shi catalyst. It is interesting to note the positions of the yellow spheres that represent BCP. Where the yellow sphere appears on a solid line between two atoms, this defines a point where the curvature, defined by a mathematical Hessian matrix, allows for a bond formation. It seems as though the sphere appears on more or less the centre of a bond when the two atoms connected are identical. For example, looking at the ring in the picture above, the BCP point appears in the centre between the two carbon atoms of the ring. When dealing with two different atoms bonded together, the point of BCP seems to be closer to the atom which has intrinsically less electron density. Looking at the carbon-hydrogen bonds in the picture above. the yellow sphere seems to be placed closer to the hydrogen atom. This could mean that the point along this line where the electron density meets a minimum is found closer to the atom with lower electron density.
This can also be seen in the weaker non-covalent interactions, shown by the dotted lines. There appears to be a point along this weak interaction line where a BCP appears, and this point also appears to be closer to the hydrogen atom than the oxygen, when looking at the interaction between the methyl hydrogen atom and the oxygen atom in the six membered ring of the Shi catalyst.
There is an interaction the Shi catalyst provides an oxygen atom to the double bond of the alkene to form the epoxide. It is interesting to see that the BCP appears to be approximately in the centre of the dotted line which shows bond formation/interaction. This may suggest and describe the covalent bond formation between the oxygen and the two carbon atoms. Also, the dotted line seems to travel into a carbon atom, from the oxygen. This could suggest some form of orbital overlap and interaction to form the epoxide.
References
[18] https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:toolbox accessed 14/02/2015
[19] http://alpha.chem.umb.edu/chemistry/ch612/files/Overheads/Topic13_1_Gillespie_Ch8.pdf accessed 14/12/2015
Suggesting new candidates for investigations
(-)-(1S,2R)-1,2-epoxy-1,2-dihydronaphthalene
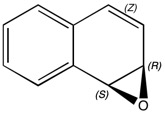 | |
Formula: C10H8O
Optical rotation: -153°[23] CHCl3 589nm
Molecular Weight: 144.173g/mol
References=
[23] S. S. Oh, W. M. Butler, M Koreeda, J.Org. Chem., Vol. 54, No. 19, 1989