Rep:Mod:opus1012

Module 3: REACTION MECHANISMS AND TRANSITION STATES

Adeleke Adekunle Francis
00516555

Abstract

This work was performed in order to provide theoretical and computational evidence for the chemist's intuition i.e. planting chemical intuition upon solid ground.

Optimising the Reactants and Products

Aim: The structures of the reactants and products will be optimised, the optimised structure will be symmetrized to find its point group. The frequencies of the vibration modes will be obtained. Also the potential energy will be calculated and compared with experimental data.

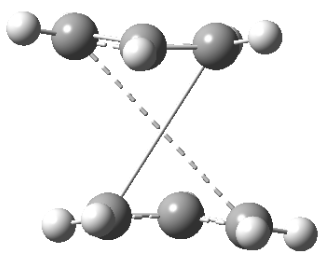
First a structure of 1,5-hexadiene was constructed on ChemBio3D, 1. The molecule was optimised with MM2 in order to obtained the basic geometry of 1,5-hexadiene (for qualitative reasons). This basic framework was reconstructed with GaussView from a half-chair structure.



A Preliminary six membered ring was drawn, 2, then a carbon atom was deleted to produce 3. Carbon-carbon bonds were removed and the atoms were realigned, also an additional atom was added to produce 4. The carbon atoms were connected and the resultant structure was cleaned to produce 5. An optimisation was performed at the HF/3-21G level of theory by the following process; Click calculate→ guassian calculation step→ optimisation (under job type)→ choose method and basis set as HF/3-21G→ change %mem to 250mb (under Link 0)→ submit. The optimised structure was symmetrized to determine the point group of the optimised structure. The compound obtained from the analysis was the 'gauche2' conformer.

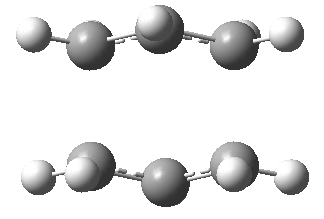
A more sensible method was used in obtaining the other conformers. A molecule of 1,5-hexadiene was constructed with GaussView.The molecule was constructed in a way that each of the four central carbons atoms are at an anti-periplanar conformation to its adjacent atom (i.e an anti-linkage between the four atoms). The resulting molecule was cleaned and an optimisation was performed at the HF/3-21G level as described above. The final structure was symmetrized to obtain the point group of the structure. A systematic approach was employed in the construction of the anti-isomers. The construction started with a methane, then one of the hydrogen atoms was replaced with another methane. The subsequent substitution of an hydrogen in the ethane molecule can proceed via various geometries. The end result (of varying the geometry in which the hydrogen atoms are replaced by methane in the construction of 1,5-hexadiene) was that the four anti conformers were obtained.

A molecule of 1,5-hexadiene was constructed in a way each of the four adjacent central carbons atoms are linked in a 'gauche' conformation. Variation in the construction of the framework of the gauche isomers as described above yielded all six gauche isomers. The result is displayed in the table below;

Table 1: The conformations of 1,5-hexadiene

Conformer	Structure	Point group	Energy/Hartrees (HF/3-21G)	Relative Energy/kcal mol-1
gauche1	compound	C2	-231.68772	3.10
gauche2	compound	C2	-231.69167	0.62
gauche2 atropisomer	compound	C2	-231.69167	0.62
gauche3	compound	C1	-231.69266	0.00
gauche4	compound	C2	-231.69153	0.71
gauche5	compound	C1	-231.68962	1.91
gauche6	compound	C1	-231.68916	2.20
anti1	compound	C2	-231.69260	0.04
anti2	compound	Ci	-231.69254	0.08
anti3	compound	C2h	-231.68907	2.25
anti4	compound	C1	-231.69097	1.06

All the structures obtained agree in structure, point group and in energies with those reported in the lab manual. An atropisomer of the gauche2 conformer was found. This atropisomer results from rotation about two carbon-carbon single bonds. The atropisomers possess the same energy and symmetry.

Table 2: The stability of the gauche conformer vs anti-conformer

	${\sigma }_{C-H}-{\sigma }_{C-H}*$ (app)	van der Waals interaction	Additional van der Waals interactions	${\sigma }_{C-H}-{\pi }_{C=C}*$
gauche3	compound	compound	compound	compound
anti1	compound	compound	compound	compound

The energy of the gauche3 conformer is lower than that of the anti1 conformer (the most stable anti conformer). This is an unexpected result. First a discussion of non-bonded interactions in n-butane, then these principles will be used to explain the stability gauche isomer over the anti-isomer in 1,5-hexadiene

Detailed analysis on n-butane reveals that the antiperiplanar (app) conformer is most stable, followed by the synclinal or gauche conformer, the other conformers are not detected due to steric strain. The reason for this is well understood. The first reason is due to orbital overlap. There is orbital overlap between the C-H (or C-C) $\sigma$ donor orbital and the C-H (or C-C) $\sigma$* acceptor orbital. This kind of orbital interaction is weak in n-butane because the C-H (or C-C) $\sigma$ donor orbital are low in energy and the C-H (or C-C) $\sigma$* acceptor orbital are high in energy, this means that there is a large difference ion energy between these orbitals and according to the Klopman-Salem equation, $E_{stab}\alpha \frac{S^2}{\mathrm{\Delta }{E}_i}$, the stabilisation energy is therefore small. However it is enough to stabilise the anti-conformer. It is also for this reason that the syn-periplanar is the most unstable conformer. In this conformer, there is eclipsed interaction between the C-H (C-C) $\sigma$ orbitals, therefore electron repulsion results in overall destabilisation of the system.

Another reason for the stability of app n-butane is long range van der Waals attraction. If two atoms (neutral) are separated by an infinite distance, the interaction between these neutral atoms is infinitely small, inversely proportional to the sixth power of the interatomic distance. As these atoms approach one another, attractive interaction starts to develop (interatomic separation decreases). This attraction is highest at the equilibrium interatomic distance, as the atoms approach one another even further, a repulsive interaction develops (one atom starts to penetrate the volume of space of the other atom), which is inversely proportional to the twelfth power of interatomic distance. This description is the Lennard-Jones (6,12) potential. With this information, the equilibrium interatomic distance that affords maximum attractive interaction can be deduced. This maximum attractive distance equals the sum of the van der Waals radii of the two atoms. For H, the van der Waals radii is 1.2Å, therefore the maximum H...H attractive distance is 2.4Å.

Back to 1,5-hexadiene, for the app-1,5-hexadiene, there are two app H-H interaction in the two central carbons, the gauche conformer has only one (red halo). There are 2 ${\sigma }_{C-H}-{\pi }_{C=C}*$ interactions available for both conformers (blue halo, the halo on the carbon atom represents the ${\pi }_{C=C}*$. Also the gauche isomer has two gauche hydrogen atoms with interatomic distance of 2.42Å, the app conformer has a similar interaction at 2.48Å. The interaction energy is about 0.3kcal/mol per interaction. As the interatomic distance changes (get smaller or larger) from the optimum 2.4Å, the interaction energy decreases. The 'additional interactions' shows the likely attractive interactions. For the gauche conformer, there are more interaction distances closer to the optimum 2.4Å than in anti-conformer. Therefore the geometry of the gauche conformer allows for more H...H van der Waals interactions than in the anti-conformer and also the interaction distances are closer to the optimum 2.4Å than in the anti-conformer. For this reason the gauche3 is more stable than anti1 conformer.

The C_i anti2 conformer of 1,5-hexadiene was reoptimised at DFT/B3LYP/6-31G(d) level of theory. This comparison between this newly optimised structure to that optimised at B3LYP/3-21G is shown below;

Anti2 conformation

	Structure	Point group	Energy/Hartrees (HF/3-21G)	Relative Energy/kcal mol-1	Relative Energy/kcal mol-1 (cf. table 1)
B3LYP/3-21G	compound	Ci	-231.69254	1832	0.08
B3LYP/6-31G(d)	compound	Ci	-234.61170	0.00	-1831

There is very little change in the geometry of the anti2 conformer when it was subjected to a second optimisation as desctribed above. The change in geometry is not easily observable. The H...H distances reveals very little difference in geometry. The energies reveal that the B3LYP/6-31G(d) calculation produces a much lower energy than the B3LYP/3-21G calculation. It is obvious that change in geometry is not responsible, but the fact that B3LYP/6-31G(d) is a higher level calculation (3 more primitive guassian functions are used to calculate the integrals) produces a more accurate value. Therefore a low level calculation produces results with appreciable accuracy, so the B3LYP/3-21G level is sufficient for subsequent calculations.

A more descriptive energy value can be obtained by performing a frequency calculation. This energy value can be compared to experimental data. The result of teh frequency calculation is shown below;

Energies/ hartrees at 298 K

A few words on transition state optimisation

Aim: The chair and boat transition structures will be constructed. The transition structures will be optimised via various techniques. The first technique is by calculating the force constants at the beginning of the calculation. The second technique is by using the redundant coordinate editor. The third method is the QST2 and finally the QST3 method will be used. The reaction coordinate will be computed by running the IRC (Intrinsic Reaction Coordinate). Finally the activation energies of the cope rearrangement for the chair and boat transition structures will be calculated.

A transition state as the name suggest is a transition from one state to another, these states are stationary points. These stationary point are usually reactants and products and sometimes they involve intermediates. The transition state may resemble the reactant, products or even the intermediates. Therefore specifying the transition structure of a reaction by mere intuition (chemical intuition) is a formidable task. With computational analysis the transition structure corresponding to the lowest energy pathway can be computed. A potential energy surface can be plotted. This PES (usually three dimensional) details the energies of the chemical species as a function of bond distances (usually the bond that is being broken and/or formed in the reaction i.e. reaction coordinate). In this study, the computation was performed in the gas phase, because solvent calculations are expensive.

Reactant, products and intermediates are stationary points on PES. They are also minima (either local or global). As previously suggested some intuition is needed in computing transition states. A chemist must understand a reaction in terms mechanism and must have some intimation about the structure of the transition state. It is this guessed structure (with various levels of accuracy) that will be used as the preliminary structure, on which a TS optimisation will be performed. This guessed structure must be reasonable for it to be acceptable for computation (or else an error message is generated and no optimisation is performed). The transition structure is a saddle point (a first order saddle point) that connects two stationary points on a PES. A first order saddle point are also stationary points in that all the forces or energy gradients are zero (or very close to zero), in this way saddle points are similar to stationary states but unlike a minima, "one of the second derivatives in the first order saddle is negative". To decipher this statement, a brief discussion of saddle points is needed.

For a multi-variable function, the second order derivative is a test of the eigenvalues of the Hessian matrix of the function. The Hessian matrix is a 2×2 matrix named after the German mathematician Ludwig Otto Hesse. It is a matrix of the second-order partial derivatives (the curvature) of the function. If some of the eigenvalue values of the Hessian are negative, then the variable x is maximum and if some of the eigenvalue values of the Hessian are positive, then the variable x is minimum. Therefore if some are positive or negative, the point is saddle point.

Important: It will be shown later that when the vibrational modes of a transition structure are computed, one negative frequency (in this study) is observed. A Taylor expansion about equilibrium position (x=0) for a one dimensional system is given as; $V=V(0)+{\left(\frac{\partial V}{\partial x}\right)}_{0}x+\frac{1}{2}{\left(\frac{{\partial }^{2}V}{\partial x^2}\right)}_0{x}^2+\frac{1}{3!}{\left(\frac{{\partial }^{3}V}{\partial x^3}\right)}_0{x}^3+...$. V(0) is zero due to vertical alignment, at equilibrium, x=0, the first derivative or slope is zero. Third order and higher order terms are negligible. The second derivative of energy is the curvature of the PES. This is the force constant, so a larger force constant corresponds to a steep potential energy curve, and a steep curve means that minimal displacement from equilibrium position requires a large amount of energy. For a polyatomic compound with 3N dimensions, the Taylor expansion is given as; $V=V(0)+\sum _i{\left(\frac{\partial V}{\partial x_i}\right)}_0{x}_i+\frac{1}{2}\sum _{i,j}{\left(\frac{{\partial }^{2}V}{\partial x_i{x}_j}\right)}_0{x}_i{x}_j+...$. Again the second order term is the only one that is considered, this term is the generalised force constant k_ij. All the k_ij terms can be put in matrix array to form a square matrix called the Hessian.

$\left[\begin{array}{cccc}{k}_{11}& k_{12}& \dots & k_{1(3N-6)}\\ k_{21}& k_{22}\\ ⋮\\ k_{(3N-6)1}\end{array}\right]⟹\left[\begin{array}{cccc}{K}_{11}& 0& \dots & 0\\ 0& K_{22}\\ ⋮& & \ddots & \\ 0& & & K_{(3N-6)(3N-6)}\end{array}\right]$

where $k_{11}={\left(\frac{{\partial }^{2}V}{\partial x_1{x}_1}\right)}_0$ and $k_{12}={\left(\frac{{\partial }^{2}V}{\partial x_1{x}_2}\right)}_0$ and $K_{11}={\left(\frac{{\partial }^{2}V}{\partial Q_1{Q}_1}\right)}_0$ and $K_{12}={\left(\frac{{\partial }^{2}V}{\partial Q_1{Q}_2}\right)}_0=0$.
The matrix formulation shows that vibrational motions are coupled, therefore they must be decoupled. First the coordinate x is transformed into mass-weighted coordinates $q_i,q_i=\sqrt{m_i}{x}_i$. If this is substituted into the Hessian, "the coordinates that diagonalise the matrix are the vibrational modes, Q_i. Therefore negative eigenvalues of the matrix will produce negative frequencies, since the eigenvector of the negative eigenvalue is the reaction coordinate, the vibrational mode with negative frequency is the 'movement' involved in that reaction.

Therefore TS optimisation involves the following; there is a 'search' for the stationary point with a negative second derivative and by performing a frequency analysis, the coordinates of the TS structure that diagonalise the Hessian matrix will produce the vibration modes one of which has a negative frequency. The computational analysis involves a situation whereby the energy is maximised along the 'reaction mode' and minimised elsewhere. For this reason a structure that is close to TS is needed (has some negative curvature). This makes the optimisation process difficult. The reason for this is as follows; the approximation used is that higher order terms are negligible, this saves computational time but then the potential term is just an harmonic function. Therefore in a TS opt. as the energy is increased by varying coordinates a structure close to TS optimises to TS faster than one far away. Also a structure far away from TS is one with different nuclear coordinates, with this kind of structure there is a danger of optimising to the wrong transition structure. Other problems associated with using a 'wrong' preliminary structure will be addressed later.

Optimising the Chair and Boat transition structures

The chair and boat transition structures contain two C₃H₅ allyl fragments. The chair transition structure has C_2h symmetry and the boat transition structure has C_2v symmetry. The construction of the preliminary structures transition states is as follow; first an allyl fragment was constructed and optimised at the HF/3-21G level of theory. In a new GaussView window, two molecules of this structure were pasted via the 'append molecule' button. Shift + Left Mouse button was used to translate one allyl fragment relative to the other and the Alt + Left Mouse button was used to rotate the one fragment relative to the other. The alignment of the chair transition structure was such that the terminal carbons were about 2.2Å apart. The result of this is displayed below;

Optimised allyl fragment	Guess chair transition structure
compound	compound

The uploaded file of the allyl fragment does not depict the C-C-C bond delocalised $\pi$ bond (this was observed when the file was opened with GaussView), however this can be observed in the C-C-C bond lengths; they are equal bond length of 0.139nm.

Optimising the Chair transition structures (method 1)

This method is a TS optimisation that proceeds by a local search method about the region of negative curvature from a good guess structure. This method is invoked as follows; Job type was Opt+Freq→ optimisation was set to TS (Berny)→ force constant was calculated once→ an additional keyword Opt=NoEigen was included. The preliminary structure is denoted by a Z-matrix, an internal coordinate system that depends on a Hessian matrix. The force constant was calculated at the beginning of the optimisation process, i.e. the Hessian was calculated at the beginning. Opt=NoEigen turns off the checking of the eigenvalues so that the optimisation does not stop if more than one negative eigenvalue is found. The diagram below shows that the partial second derivatives were indeed calculated.

The Berny algorithm follows the uphill direction (that maximises energy) and also minimises the energy gradient. As the coordinates are optimised, a new Hessian is generated therefore a optimisation scheme is produced whereby information about the gradient of a previous step plus the previous Hessian is used to generate a 'better' Hessian. The result of this optimisation is shown below;

Optimised Chair Transition structure	Imaginary vibrational mode
compound	Vibration

The imaginary vibrational mode corresponds to the cope rearrangement. The imaginary frequency is -818cm^-1 (right click on image→ choose model→ 1-25→ vibrational mode 23 is -818cm^-1. The movement displayed by this vibrational mode is such that the transition structure moves from one minimum to the other i.e. goes from one stationary point to the other so maximum displacement of the vibrational vectors in one direction leads to reactant and in the other direction leads to product. The terminal carbon bond lengths have also changed from 2.2Å to 2.02Å (8% decrease), so the optimisation step did something, but is this the right structure? This will be verified by an IRC calculation. In this case the optimisation has worked well because there is at least one negative eigenvalue. In situations with several negative eigenvalues, of which one is larger than the other, the TS optimisation follows the path of most negative eigenvalue.

Optimising the Chair transition structures (method 2)

The difficulty in producing a good guess depends on the complexity of the reaction mechanism. Also there might be several possible TS structures. If only a crude guess can be suggested, then constrained optimisation can be performed. Also there might be several possible TS structures. This method is in two parts. The first is to freeze the reaction coordinate and minimize the rest of the structure, then the reaction coordinate is unfrozen and a TS optimisation is performed. The method is potentially less expensive because differentiating along reaction coordinate means that computing the whole Hessian might be unnecessary. The first part was performed as follows; from the guess structure→ select edit→ choose Redundant Coord Editor→ select create new coordinate→ Add Unidentified (?, ?, ?, ?)→ select two of the terminal carbons from the allyl fragments which form/break a bond during the rearrangement→ choose bond and freeze→ set bond to 2.2Å→ Repeat procedure for the other terminal carbon→ OK. An optimisation to a minimum was performed. After this optimisation, the second step was performed as follows; choose Redundant Coord Editor→ select terminal carbon atoms as before→ choose bond and derivative→OK. A TS opt. was performed without specifying force constant calculation i.e. a guessed Hessian was used, this Hessian was modified to the reaction coordinate on which the derivative is to be calculated. The result of both parts of the method is displayed below;

Guess chair TS structure	Part 1	Part 2
compound	compound	compound

The structure from method 1 and 2 are identical, the optimised TS have the same terminal allyl C-C bond lengths of 0.202nm and the same same C-C-C bond angle of 120.5^o. The minimisation of part 1 led to a change in bond angle/^o from 124.3 to 122.0. The terminal allyl C-C bond lengths of 0.22nm was observed after part 1 as expected. After the optimisation along reaction coordinate, the terminal allyl C-C bond lengths reduced to 0.202nm and the bond angle reduced to 120.5^o. The C-C bond length is unchanged since the allyl fragments have already been optimised.

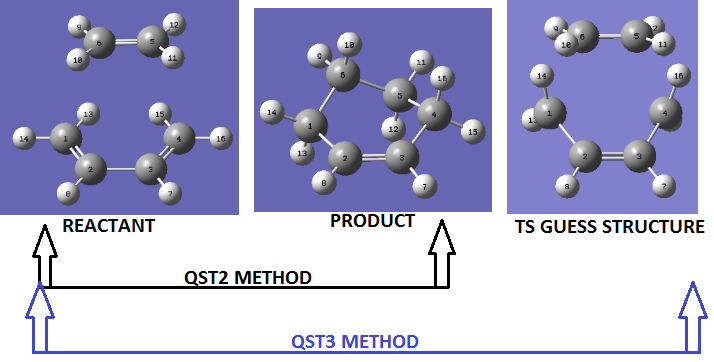
Optimising the Boat transition structures (QST2 method)

The QST2 method is a sophisticated method for obtaining the transition structure. 'Obtaining' is stressed because this method requires no initial guess. The QST2 method is a Synchronous Transit-Guided Quasi-Newton (STQN) Method. The more general STQN method, of which QST2 is a part, was developed by H.B. Schlegel et al. It utilizes a "linear synchronous transit or quadratic synchronous transit approach to get closer to the quadratic region around the transition state and then uses a quasi-Newton or eigenvector-following algorithm to complete the optimization". It performs optimizations by using redundant internal coordinates. The method uses and empirical estimate of the Hessian and the starting structure. In the QST2 method, the reactant and products are specified (the optimised anti2 conformer). The method tries to find a transition state between the reactant and the product, for this reason, numbering or ordering of the atom must be totally specified so that the reaction coordinate is understood (i.e. which bond is breaking or forming). The reactants and the products are displayed below;

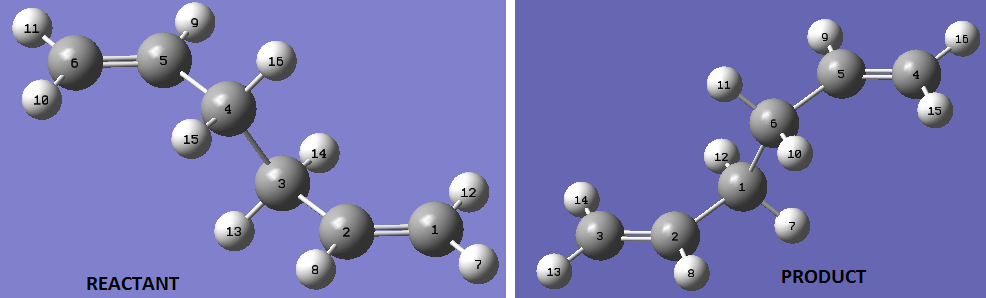
The optimisation calculation was set up as follows; Job type, select Opt+Freq→ optimise to TS (QST2)→ OK. The result of this optimisation is displayed below;

The calculation was terminated with the following error message;

This is obviously the wrong structure, it does not make sense physically. Bond rotation about the central bond was not performed, only a mere translation was effected. In order to locate the boat TS, the reactant and product molecules were modified as shown below;

The central C-C-C-C dihedral angle was changed to 0^o, then C-C-C angles were changed to 100^o. Do the same for the product molecule. These structures were optimised to produce a boat transition structure.

Optimised Boat Transition structure	Imaginary vibrational mode
COMPOUND	Vibration

The imaginary vibrational mode corresponds to the cope rearrangement. The imaginary frequency is -840cm^-1 (right click on image→ choose model→ 26-50→ vibrational mode 45 is -840cm^-1. The terminal carbon bond length of allyl fragment is 0.214nm (longer than chair TS by 5.6%). The C-C bond length was 0.138nm similar to the optimised allyl fragment!

Optimising the Boat transition structures (Method 1)

Method 1 as described above was invoked in an attempt to minimise the boat TS. A guess structure was produced for the boat TS with C_2v symmetry from two optimised allyl fragment with an inter-fragment distance of 2.2Å. The result of the optimisation is displayed below;

Guess Boat TS	Optimised Boat TS	Imaginary vibrational mode
COMPOUND	COMPOUND	Vibration

The imaginary vibrational mode corresponds to the cope rearrangement. The imaginary frequency is -841cm^-1 (right click on image→ choose model→ 26-50→ vibrational mode 29 is -841cm^-1. The structure from this optimisation agrees with the structure from the QST2 optimisation.

Optimising the Boat transition structures (QST3 method)

Another STQN method is the QST3 method. The method allows for a guess structure of the TS to be specified together with the structure of the reactant and the product. The ordering or numbering of the structures is also important in this case. The structures of the reactant, products and intermediates are displayed below;

The optimisation calculation was set up as follows; Job type, select Opt+Freq→ optimise to TS (QST3)→ OK. The result of this optimisation is displayed below;

Optimised Boat structure	Imaginary vibrational mode
COMPOUND	Vibration

The imaginary vibrational mode corresponds to the cope rearrangement. The imaginary frequency is -840cm^-1 (right click on image→ choose model→ 1-25→ vibrational mode 19 is -840cm^-1. The structure from this optimisation agrees with the structure from the QST2 optimisation.

Conclusion: Method 1, QST2 and QST3 produce the boat transition structure, repeated attempts to invoke method 2 failed, the TS optimisation along reaction coordinate did not produce the TS. Time does not allow for a more detailed analysis behind this failure.

Intrinsic Reaction Coordinate (IRC)

Detailed explanation about the IRC has been given in section 3. The IRC provides a way proving the veracity of the optimised transition states. Inspection of the chair and boat TS does not reveal the identity of the product they form. However when IRC is invoked in Guassian, the method traverses the potential energy surface from the transition state to the minimum along the path of steepest descent i.e. the minimum energy path.

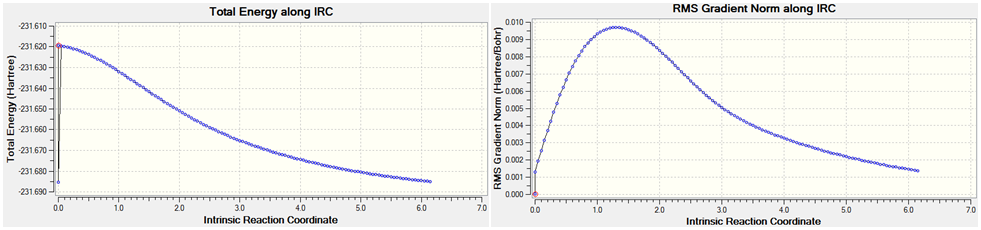
IRC calculation was performed for the chair and boat transition states. The IRC calculation for the chair TS was invoked with the keyword # irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity. irc ofcourse denotes the intrinsic reaction coordinate, forward means that the calculation will be calculated in the forward direction alone i.e. towards the product stationary point. calcfc means that the force constant was calculated once and maxpoints=50 specifies the maximum number of point along the IRC before calculation stops. The result of this is shown below;

TS structure	Structure 2	Structure 40

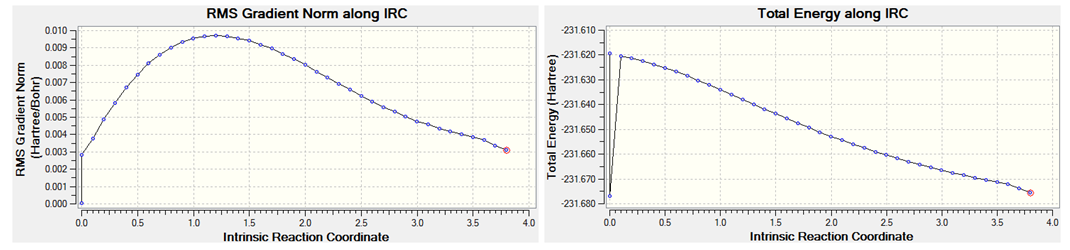
An error termination message was generated. The IRC calcultion stopped after 40 points. The structure at point 2 looks like a minima, it is lower in energy than the final structure obtained. The default stepsize of 10 prevented the calculation from reaching a minima; because the stepsize was too large, the optimisation jump from one structure to another at either side of the minima. For this reason the irc stepsize was changed to 5 by adding irc=stepsize=5 as an additional keyword. The result of this is shown below;

Structure 50
compound

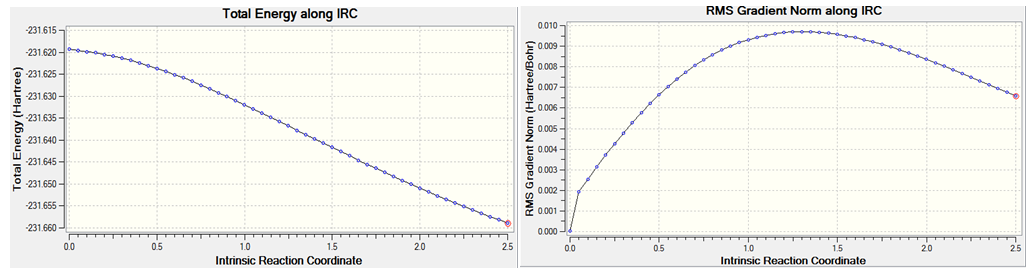
No error termination was observed. The final structure was that obtained at point 50 along the IRC path. The IRC is well behaved unlike the previous example. The structure observed bears some resemblance to the gauche2 atropisomer. The C-C bond length formed is 0.166nm. The energy of the final structure is -231.659 hartrees, this energy is higher than the energies of any of the structures found, therefore it is not a minimum. The next step was to optimise the resultant structure of this analysis, the result of this is shown below;

Optimisation of structure 50 at B3LYP/3-21G level

compound

Bond lengths and energy data shows that this structure is in fact gauche 2 atropisomer. Additional analysis was performed by increasing the maxpoint from 50 to 300 and keeping the stepsize at 5. This result of this is shown below;

Structure 50
compound

The energy of the structure is -231.685 and the bond length is 0.157nm. This structure is close to the gauche2 minimum but not quite there.

Note: I did try calculating the force constant at every point with a maxpoint of 100. The result of this was the gauche2 structure as expected. Sadly a mistake in the file naming deleted the data. I mention this for completeness.

Conclusion: The chair transition structure leads to the gauche2 isomer, therefore the TS structure is a viable structure.

IRC calculation for the boat TS was invoked with the keyword # irc=(forward,maxpoints=50,calcall,stepsize=5) hf/3-21g geom=connectivity. The force constant was calculated at every step. A stepsize of 5 was used and maxpoint of 50 was specified. The result is shown below;

Boat TS structure	Structure 50

The bond energy is -231.662 hartrees and the bond length is 0.162nm. The structure is not a minimum. This structure was optimised to give;

Optimisation of structure 50 at B3LYP/3-21G level

compound

The optimisation led to the lowest energy conformer, the gauche3 conformer.

Activation Energies

The result of the IRC was that the two different chair and boat transition states led to different products. The boat TS gave the most stable gauche3 conformer, so if this reaction were thermodynamically controlled, it would proceed via the boat TS. The confirm or refute this assertion. The activation energies of the reaction will be computed. First both transition states were optimised at the B3LYP/6-31G(d) level of theory, then a frequency analysis was performed. The result is as follows;

Note: Code for this table was taken from lab manual of module 3. Ref: M. Bearpark, Table Code, 2011.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461342	-234.556983	-234.414929	-234.409008
Boat TS	-231.602802	-231.450927	-231.445298	-234.543093	-234.402339	-234.396005
Reactant (anti2)	-231.692535	-231.527833	-231.520862	-234.611703	-234.469211	-234.460967

*1 hartree = 627.509 kcal/mol

Activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G(d)	B3LYP/6-31G(d)	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	38.36	37.35	34.06	32.61	33.50
ΔE (Boat)	48.26	47.42	41.96	40.76	44.70

Experimental data were taken from lab manual. The electronic energies of the TS have been presented here for the first time, these energies were obtained from the summary files. The values of the activation energies are similar to those reported in manual. The value at the B3LYP/6-31G(d) level is closer to experimental values. The final result is that the activation of the boat TS is higher than that of the chair TS at 0K or 298K, with the two levels of theory and also with expt. data. The additional keyword 'temperature=0.001' was used to calculate the activation energy at 0K. There is little difference between the value at OK and 298K. Under thermodynamic conditions, the reaction proceeds via the boat TS to form the more stable, thermodynamic product, gauche3 conformer. Under kinetic conditions, the reaction proceeds via the chair TS with lower energy barrier to form the kinetic product, gauche2 conformer.

The Diels Alder Cycloaddition

The Diels Alder reaction is an example of a cycloaddition reaction. In cycloaddition reactions, two or more $\sigma$ bonds are formed. The work of R.B. Woodward and R. Hoffmann led to the development of secondary orbital interactions. This work together with its unification with Galois' group theory led to the development of orbital correlation diagrams. The fact that the orbital symmetry of reactant and product must match (conservation of orbital symmetry)explains the selectivity of pericyclic reactions.

On cis-butadiene

A structure of cis butadiene was constructed on GaussView and this structure was optimised using the AM1 semi empirical method. The result was a planar structure. The optimisation was performed on a freshly drawn structure with the HF/3-21G method. The result was also a planar structure. The frequency was then calculated using the HF/3-21G method. An imaginary frequency was observed, the vibrational mode of this frequency was a distortion from planarity. Manual distortion was applied on this vibrational mode and the distorted structure was saved. Another optimisation was performed at the HF/3-21G level and a frequency analysis was performed. No imaginary frequencies were observed. The table below summarizes my findings;

	AM1 optimised structure	HF/3-21G optimised structure	HF/3-21G optimised structure (imaginary vibrational mode)	HF/3-21G reoptimised structure	HF/3-21G reoptimised structure (vibrational modes)
	compound	compound	Vibration	compound	Vibration
Energy/ hartrees	----------	----------	-153.987457	----------	-153.977904

The energy displayed is the sum of electronic and thermal free energies. It is well known that the cis-butadiene is less stable than the s-trans-butadiene. However the structure of the cis-butadiene has been a subject of debate for several years. Work by Lipnick and co-workers showed via NMR spectroscopy that the gauche (non-planar, twisted) conformer was the stable cis-butadiene isomer. However Raman study by Carreira showed that the planar conformer was more stable. Computational analysis by Schaefer and co-workers (using double $\zeta$ basis set with the self-consistent method) revealed that the planar conformer is a transition state between two interconverting gauche (non-planar, twisted) conformer and that barrier to planarity was 0.4kcal/mol. Also they reported that the dihedral angles of the gauche conformer as 33.2^o or 37.8^o when the double $\zeta$ plus polarisation basis set was used. The data presented above agree with their result. An imaginary frequency (-152.6 cm^-1) which corresponded to the interconversion of the gauche isomers was observed, also a dihedral angle of 38.3^o was observed. However the energy values seems to indicate that the planar structure is more stable than the gauche structure. The reason for this is attributed to the deficiency of this level of theory. Several literatures revealed that computational analysis at low level of theory produced very little diference in energy. For this reason an optimisation was performed at the B3LYP/6-31G(d) level of theory on a freshly drawn cis-butadiene structure. As before, an imaginary frequency was observed, the vibrational mode of this frequency was a distortion from planarity. Again, manual distortion was applied on this vibrational mode and the distorted structure was saved. Another optimisation was performed at the B3LYP/6-31G(d) level and a frequency analysis was performed. No imaginary frequencies were observed. The result is displayed below;

	B3LYP/6-31G(d) optimised planar structure	B3LYP/6-31G(d) optimised planar structure (imaginary Vib. mode)	B3LYP/6-31G(d) optimised gauche structure	B3LYP/6-31G(d) optimised planar structure (Vib. mode)
	compound	Vibration	compound	Vibration
Energy/ hartrees	----------	-155.926899	----------	-155.927192

The energy displayed is the sum of electronic and thermal free energies. All former observations are valid in this level of theory except the dihedral angle of 30.2^o. The important observation is that the gauche isomer is now more stable than the planar isomer. The H...H distance is the key to this observation. With the HF/3-21G method, the H....H distance is longer than the optimum of 0.24nm in the gauche conformer, but with the B3LYP/6-31G(d) level of theory, the H....H distance is more closer to the optimum. In the planar structures (at both levels of theory), the deviation from optimum is slight, even lesser than the gauche in B3LYP/6-31G(d) method, but the fact that it is higher in energy is consistent with the fact that the van der Waals interaction is modelled with a Lennard-Jones (12,6) potential), so a slight deviation below the van der Waals radius leads to a greater increase in energy (inverse twelfth power) than a slight deviation above the van der Waals radius (inverse sixth power). The energy difference reveals a planarity barrier of 0.2kcal/mol, this value is close to literature value stated above.

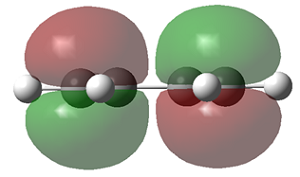
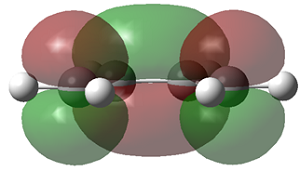
As discussed above, the difference in energy is slight, so the planar structure is a good approximation of the structure of cis-butadiene. The MO's of the three structure i.e. the AM1 optimised structure, the planar HF/3-21G optimised structure and the gauche HF/3-21G optimised structure, are displayed below.

heading	HOMO	LUMO
AM1
symmetry wrt plane	Antisymmetric	Symmetric
3-21G
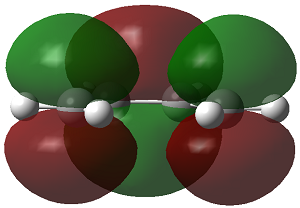
symmetry wrt plane	Antisymmetric	Symmetric
3-21G(non-planar)
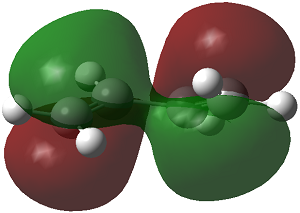symmetry wrt plane	Antisymmetric	Symmetric

The HOMO of cis-butadiene is antisymmetric with respect to reflection plane but the LUMO is symmetric with respect to reflection plane.

Transition state geometry and reaction path of an hypothetical reaction

A cycloaddition reaction requires a dienophile, usually an electron deficient diene. This reaction will there not work because the 'dienophile' component is electron rich. However if the two compounds are tethered i.e. in an intramolecular reaction, then the reaction might occur.

An envelope structure of the transition state was constructed as per lab manual i.e. via a two-atom-bridge bicyclic compounds, then a -CH₂-CH₂- fragment was removed, the structure was cleaned and a TS optimisation was performed using method 1 (see Part 1 for details). An inter-fragment distance of 0.22nm was used. Method 2 was also tried, but the second part of the method i.e. TS optimisation along reaction coordinate failed. The QST2 and QST3 methods were also used. The numbering of the structure is presented below;

The product structure is an optimised structure of cyclohexene (at HF/3-21G level). The transition structures obtained are shown below;

TS structure, method 1 (imaginary vib. mode)	TS structure (QST2 method) imaginary vib. mode)	TS structure (QST3 method) imaginary vib. mode)
Vibration	Vibration	Vibration

For some reason, the uploaded 'log files' displays the wrong C-C bond length (sometimes it displays correct bond lengths which change upon refreshing the page. When opened with GaussView, the C-C bond lengths in the butadiene fragment and the ethane fragment were all equal at 0.139nm. The inter-fragment distance is as displayed above, 0.212nm. The imaginary frequency from the three method is -956 cm^-1, this vibrational mode correspond to bond formation in the reaction. The formation of the two bonds occurs at the time i.e. synchronous. The lowest positive frequency is -147 cm^-1, this correspond to a bending motion of the atoms. Typical sp³-sp³ C-C bond length is 0.154nm and sp²-sp² C-C bond length is 0.134nm. The van der Waals radius of the carbon atom is 0.170nm. The C-C bond length of 0.139nm is therefore intermediate between a single and double bond. The inter-fragment bond length is 0.212nm. This value is larger than any C-C single and double bond, so in the TS, the $\sigma$ bond is yet to form. However the inter-fragment distance is smaller than sum of the van der Waals radii, so the interaction between the carbon atoms is a bonded interaction, i.e. a partly formed $\sigma$ bond.

The interaction of the MO's of the reactants is illustrated below, followed by the computed MO;

	Front View	Side View	Symmetry wrt mirrow plane
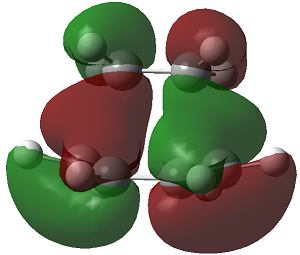
HOMO			Antisymmetric
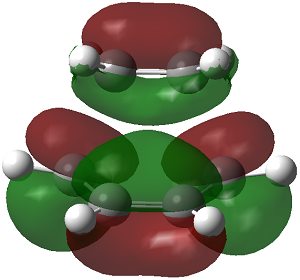
LUMO			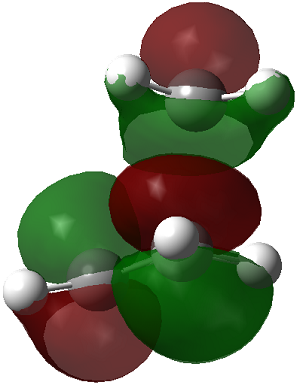Symmetric

In this reaction the HOMO is antisymmetric with respect to reflection plane. The HOMO is formed by interaction of the HOMO of butadiene and LUMO of ethane. Orbital symmetry is conserved so the reaction is allowed i.e. interacting lobes have the same wavefunction parity/sign.

An IRC calculation was performed to check whether the TS was correct, the IRC plot is shown below. The IRC did not reach the final product structure, the structure was reoptimised at the B3LYP/6-31G(d) level of theory and a frequency analysis was performed. A negative frequency was observed. The vibration mode was manually distorted and the distorted structure was saved. The distorted structure was optimised and a frequency analysis was performed, The results are as follows;

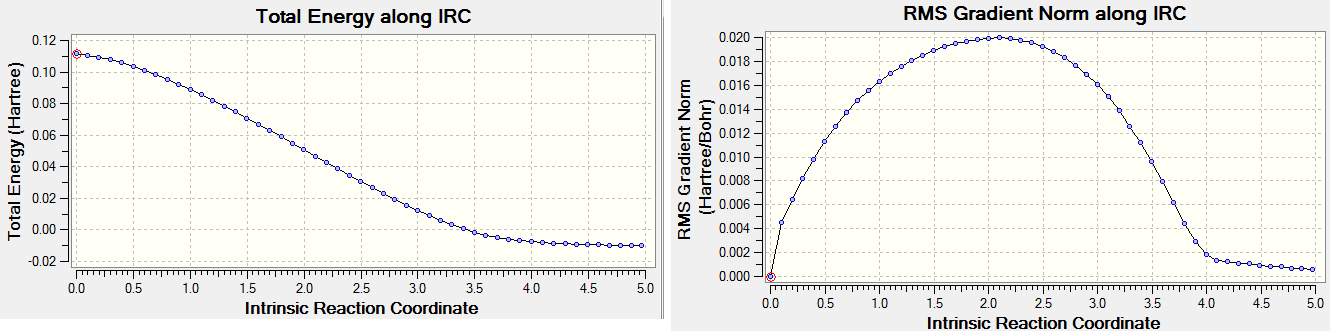
IRC final structure	IRC final structure, Optimised at B3LYP/6-31G(d) (imag. vib)	Optimised Distorted structure	Optimised Distorted structure (lowest vib. mode)
compond	compond	compond	compond

The final structure is the expected half-structure of cyclohexene.

Regioselectivity of a Diels Alder reaction

The transition states for the reaction were constructed via an optimised bicyclic compound as described in the previous section. The resulting structures were cleaned and optimised with method 1 and the QST2 method (file too large to upload). The results are displayed below;

heading	Optimised structure (method 1)	Optimised structure, method 1 (imag. vib.)	Product
ENDO	compound	compound	compound
Energy	------	0.143591*	-0.160171**
EXO	compound	compound	compound
Energy	------	0.144791*	-0.159968**

The imaginary frequency corresponds to reaction coordinate i.e. the bond forming process. The energy reveals that the endo product is the thermodynamic and kinetic product.

ENDO PRODUCT

heading	HOMO-1	HOMO	LUMO+1	LUMO+2
Front View
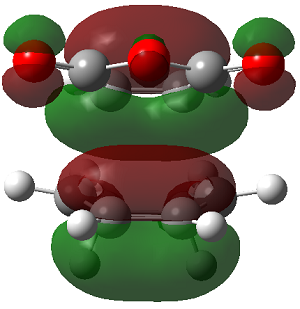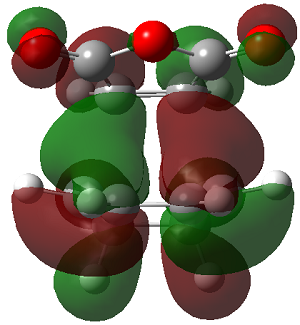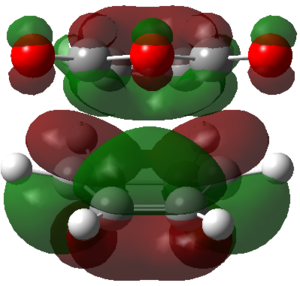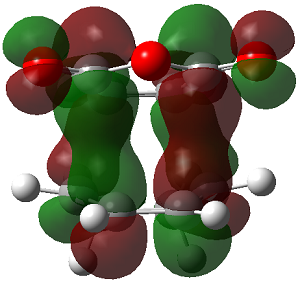
Side View

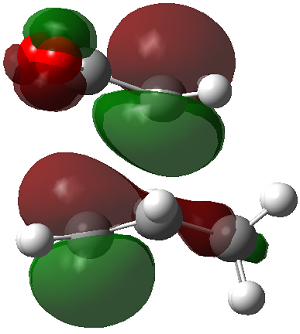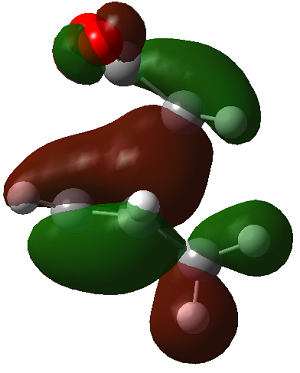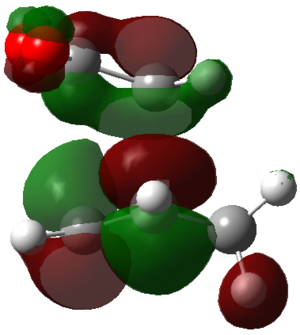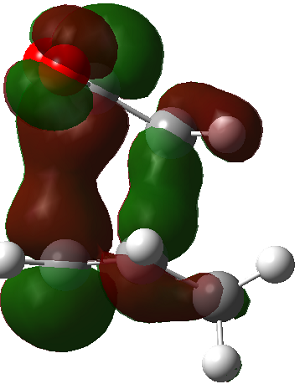
EXO PRODUCT

heading	HOMO-1	HOMO	LUMO+1	LUMO+2
Front View
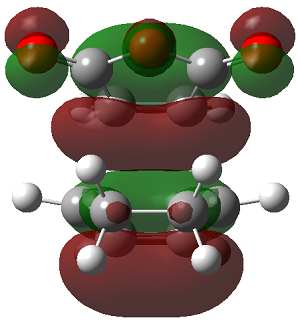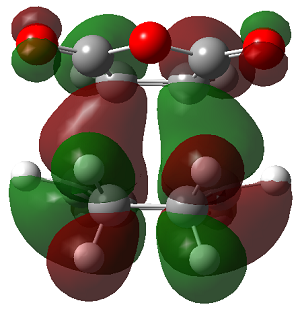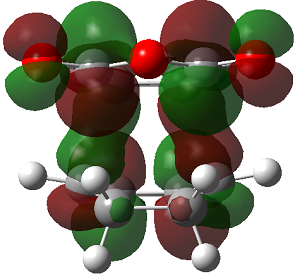
Side View

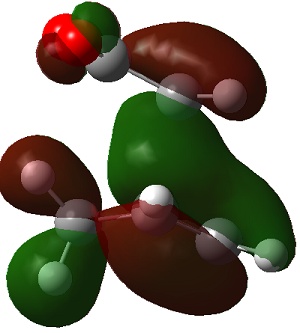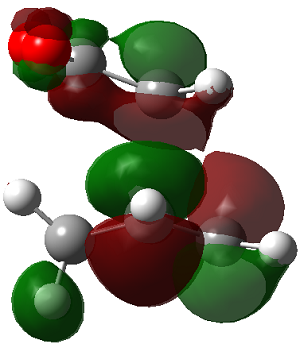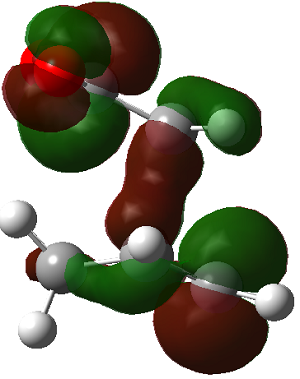
The LUMO+2 of the endo product reveals that there is secondary orbital interaction. This interaction is notr present in the exo product. However the LUMO+2 is an unoccupied orbital so its stabilisation does not affect the overall stability of the TS or product. The energies of the orbitals are given below;

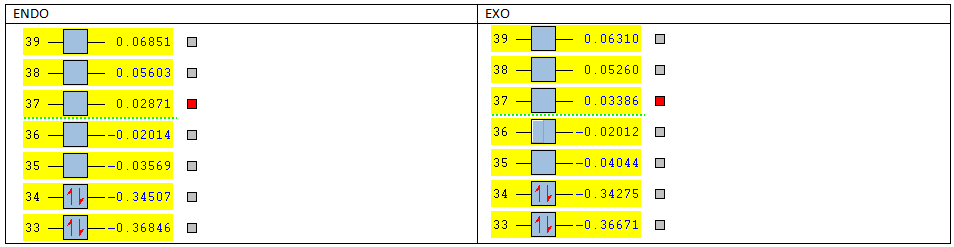
The energies of the filled orbitals are very similar in both the endo and exo TS. In a paper published by García and co-worker, he outlined several explanation for selectivity in pericyclic reaction. They questioned the need to invoke SOI's. They suggested that a "combination of well-known mechanisms (such as solvent effects, steric interactions, hydrogen bonds, electrostatic forces, and others) can be invoked instead to justify the endo/exo selectivity of Diels-Alder reactions". Following the authors' logic, the stability of the TS and product is to hydrogen bonding between the C-H $\sigma$ orbital and the forming alkene bond. Also there is non bonded interaction in the endo product as illustrated. For these reasons the endo product can be rationalised as both the thermodynamic product and the kinetic product. It is also important to note that the energy of the exo TS and product is very close to that of the endo TS and product but it does not have non-bonded interactions or hydrogen bonding like in the endo product and TS. The reason for the similarity is that the exo TS and product are stabilised to some extent by electrostatic forces between the hydrogen (gold halo) and the carbonyl carbons. This kind of electrostatic interaction was also reported by the authors. Compared to module 1, steric interaction as a result of two carbon atom vs one carbon atom eclipsing interactions does not play role in this reaction.

This explanation is logical and the observations can be explained by non-SOI theories, however it is not enough to complete disprove secondary orbital interactions. SOI's have been invoked in non-pericyclic reactions as well, therefore more thorough work is still needed in order to disprove the Woodward's and Hoffmann's SOI theory.