Rep:Mod:opus1010

1. Abstract

This work was undertaken in order to communicate the POWER! and limitations of computational analysis.

2. Introduction

Chemistry is a revered experimental science. This truism needs no proof. Centuries of experimental discussions and analysis are a testament to this fact. Several experiments that have been conducted over the centuries which range from mere curiosities to an earnest and determined search for knowledge. The ultimate aim of all these fascinations has been to study the structure, properties (both physical and chemical) of matter and its function for the ultimate goal of applying gained knowledge to solve real-life problems.

In a logical sense, the foremost study must be that of the structure of matter, although historically an understanding of the function of several molecules usually preceded the determination of its structure. Instrumental methods (X-ray crystallography, NMR, IR) allow for structural elucidation. These instrumental methods are very costly and time-consuming. The physical and chemical properties of the compounds determines the kind of instrumental analysis that can be done e.g. an unstable intermediate may need matrix isolation before it can be studied.

Computational chemistry uses "theoretical tools to solve chemical problem". Thus, computational chemistry forms the third pillar of knowledge in chemistry, the other two being experimentation and theory. The work of Johann Josef Loschmidt which was published in his 1861 booklet, Chemische Studien ("chemical studies") illustrated two-dimensional representations for over 300 molecules. Although August Wilhelm von Hofmann had already constructed several physical models as lecture aids in 1860. Loschmidt’s ‘spacefilling’ models were the forerunner to modern molecular modelling. Nowadays it is normal practice to perform computational analysis after a compound has been synthesized and to compare experimental result to data from computational analysis.

The most important application of running computational experiments is that of prediction. Reaction outcome can be predicted, therefore reaction process can be optimised before any 'wet-work' is performed. Reaction mechanism can be explored from quantum mechanical calculations, a far accessible method than instrumental-spectroscopic analysis.

3. Molecular Mechanics: A Brief History

The foundation of this method is vibrational spectroscopy. Analysis of vibrational spectra led to the development of potential functions which described the energy of the molecule at equilibrium bond positions and away from it. In an attempt to fit molecular vibration to a function, two different methods were employed. The first was the Central force field technique (CFF), the function used was a sum of pairwise interactions. Specific covalent interactions were not specified, therefore the covalent structure of the molecule could not be deduced (only information about energy was obtained), this was an obvious disadvantage.

The second method to be developed was the Valence force field (VFF), in this method, vibrational data was fitted a function which included bond length and bond angle terms. With this technique, some structural information was obtained, therefore one could compare molecules. Also with technique much information is lost in the crude approximations of the functions.

Nevertheless, both methods, refined, were the starting point of molecular mechanics. Derek Barton was influential in this subject area, as was Bright-Wilson for his work on molecular vibrations. MM2 was developed by Norman Allinger primarily for conformational analysis of hydrocarbons and other small organic molecules. He later introduced MM3 and MM4 which incorporated more parameters for different classes of organic molecules.

Now there exists several force fields which contains various kinds of parameters, and they are used for various complexities of chemical problems e.g. the BMS force field (D.R. Langley, 1998) is useful for Nucleic acids, SHAPES (V.S. Allured et al, 1991) is useful for transition metal compound, UFF (A.K. Rappe, 1992) is a general force field with parameters for the full periodic table up to and including the actinoids.

4. Molecular Mechanics: How does it work?

Molecular mechanics uses Newtonian or classical mechanics to model molecular systems. The potential energy of all systems in molecular mechanics is calculated using force fields. A force field contains distinct parameters of mathematical functions that are used to describe the potential energy of an atom or molecule. “The typical parameter set includes values for atomic mass, van der Waals radius, and partial charge for individual atoms, and equilibrium values of bond lengths, bond angles, and dihedral angles for pairs, triplets, and quadruplets of bonded atoms, and values corresponding to the effective spring constant for each potential.”

A force field sums up both bonded terms relating to atoms that are linked by covalent bonds, and non-bonded terms describing the long-range electrostatic and van der Waals forces. The general form for the total energy is given as;

${E}_{total}=E_{bonded}+E_{nonbonded}$

where the components of the covalent and noncovalent contributions are given by the following summations:

${E}_{bonded}=E_{bond}+E_{angle}+E_{dihedral}$

${E}_{nonbonded}=E_{electrostatic}+E_{vanderWaals}$

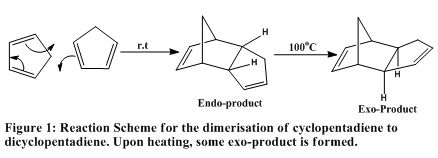
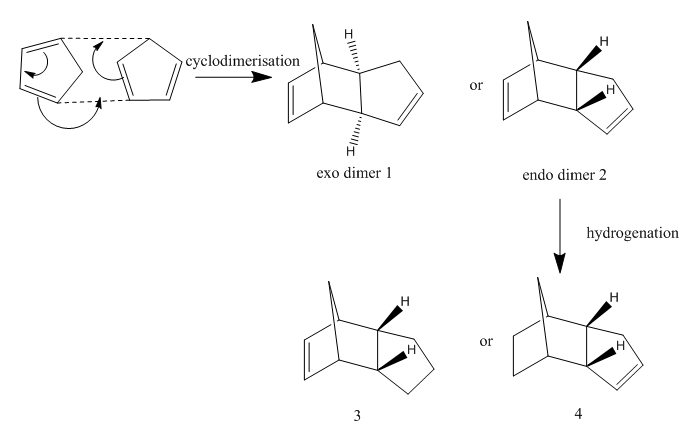
5. Case Study 1: The hydrogenation of Cyclopentadiene dimer

The work of R.B. Woodward and R. Hoffmann led to the development of secondary orbital interactions. This work together with its unification with Galois' group theory led to the development of orbital correlation diagrams. The fact that the orbital symmetry of reactant and product must match (conservation of orbital symmetry)explains the selectivity of pericyclic reactions. The dimerisation of cyclopentadiene is a common, facile [4+2] cycloaddition reaction with almost exclusive endo-selectivity.

5.1. MECHANISM FOR THE DIMERISATION OF CYCLOPENTADIENE (for completeness)

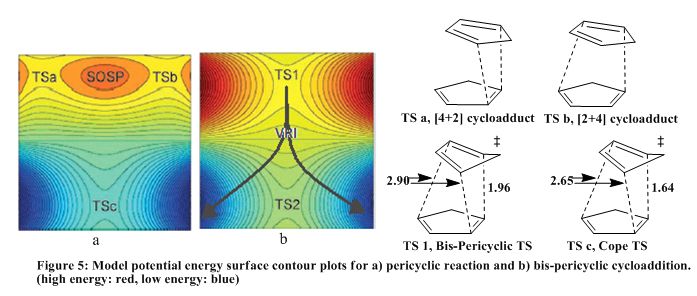
The works of Caramella et al applied the principle of bifurcation of potential energy surfaces to several organic reactions. Caramella and co-worker showed that the endo-cycloaddition of cyclopentadiene occurs along a bifurcated reactant-product energy pathway.

As one goes from a transition state to a minimum, there is curvature associated with the steepest-descent path from negative to positive. This curvature must pass through zero. The point along an ‘orthogonal principle direction’ at which it passes zero is called the branch point or valley-ridge inflection point (VRI).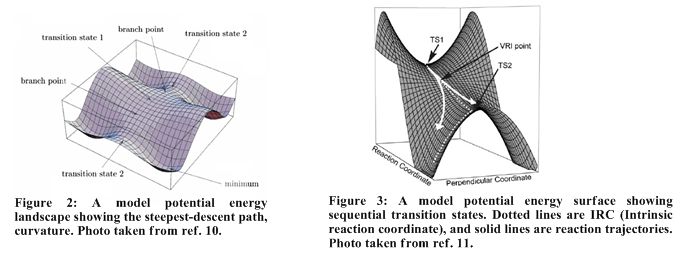

At first, solutions to differential equations do not allow departure from the steepest-descent path to either side of branch point but bifurcation of the path is possible if there is minute perturbation from the steepest-descent path (an intuitive solution that is not observed) or if the bifurcation point or VRI is a stationary point. Thus when a steepest descent path connects two transition states (when there no energy minima between them), a VRI must connect them. Thus the curvature is positive to negative through zero.

In Figure 4a below, there are two competing cycloaddition transition states TS a and TS b, a SOSP (second order saddle point) connects these transition states. Isomerisation of the cycloadduct leads to Cope TS (TS c).

In the dimerisation of cyclopentadiene, TS a and TS b merge into a single bis-pericyclic transition state, TS1. SOSP is lost and VRI connects TS1 and TS c. In this reaction, TS a and TS b are the transition states for the [4+2] and [2+4] cycloadduct. Bond lengths show that TS1 is highly asynchronous TS. Along the IRC, one proceeds from TS1 to TS c with a 2.3k cal/mol decrease in energy. In summary, TS a and TS b merge to form TS1, this then leads to a VRI which splits, however as discussed earlier, the main trajectory , IRC, follows the steepest gradient path to TS c. DA reaction performed with tethered analogues showed equal ration of [2+2] and [4+2] cycloadducts.

5.2. COMPUTATIONAL ANALYSIS

The energies of the four compounds, 1(exo-product), 2(endo-), 3 and 4 (dihydro products) are given below;

MM2 ANALYSIS OF COMPOUNDS 1-4

Result	Structure
Stretch = 1.2893 Bend = 20.6121 Stretch-Bend= -0.883 Torsion = 7.6306 Non-1,4 VDW = -1.4128 1,4 VDW = 4.2337 Dipole/Dipole = 0.3770 Total Energy= 31.8916 kcal/mol	Exo product
Stretch= 1.2506 Bend= 20.8656 Stretch-Bend= -0.8305 Torsion= 9.5035 Non-1,4 VDW= -1.5162 1,4 VDW= 4.2936 Dipole/Dipole= 0.4452 Total Energy= 34.0120 kcal/mol	Endo Product
Stretch= 1.2659 Bend= 19.8063 Stretch-Bend= -0.8276 Torsion= 10.8698 Non-1,4 VDW= -1.2207 1,4 VDW= 5.6394 Dipole/Dipole= 0.1621 Total Energy= 35.6953 kcal/mol	Dihydro 3
Stretch= 1.1029 Bend= 14.5495 Stretch-Bend=-0.5457 Torsion= 12.5059 Non-1,4 VDW= -1.0843 1,4 VDW= 4.5009 Dipole/Dipole= 0.1407 Total Energy= 31.1699 kcal/mol	Dihydro 4

5.3. DISCUSSION

Product 1 vs 2: The result of the MM2 analysis shows that the endo-product is higher in energy than the exo-product by 2.1204 kcal/mol. Therefore the exo-product is the thermodynamic product. As discussed earlier, this DA reaction id selective for the endo-product, therefore the less stable kinetic product is formed.

MM2 has failed to reveal the endo-selectivity of this reaction. The reason for this is that the MM does not take electrons into consideration (see section 4), therefore the stereocontrol as a result of secondary orbital interactions is not observed.

In the dicyclopentadiene product, there is a two carbon atom bridge and a one carbon atom bridge. In the exo-product the fused cyclopentene ring is eclipsed with the one carbon atom bridge so there is less steric hindrance and it is more stable. In the endo-product, the cyclopentene ring is eclipsed with the two carbon atom bridge so there is more steric hindrance and it is less stable. This explanation is refected in the torsion, as discussed in section 4, the energy term for the torsion or dihedral angle is such that eclipsing interactions are defined as a function of rotational barrier height, so larger eclipsing interaction results in a larger rotational barrier height and thus larger torsion energy.

A kinetic product has a lower energy TS to the product, so it is formed fastest. The reason is due Alder's endo rule or "the principle of maximum accumulation of unsaturated centers".

IMAGE FAILURE----SEE ENERGY DIAGRAM

CALCULATION OF POTENTIAL ENERGY SURFACE OF DIMERISATION DONE AT THE B3LYP/6-31G* LEVEL, ENERGIES ARE RELATIVE TO REACTANT

Species	Identity	ΔH/ (kcal/mol)
5	Diradical TS	21.0
6	Diradical forming TS	25.7
7N	Endo TS (bis-pericyclic TS)	21.0
7X	Exo TS	23.9
8N	Endo product	-11.8
8X	Exo product	-12.8
9	Cope TS	18.7

The endo TS 7N is lower in energy than exo TS 7X by 2.9 kcal/mol (expected for the kinetic product). The cope TS 9 is lower in energy than the endo-bispericyclic TS 7N (expected as shown in the PES). The exo product 8X is lower in energy than the endo product 8N (as expected). Bond lengths of endo TS 7N reveals a high degree of asynchronicity (as shown in Fig. 5).

In conclusion, the endo pathway is favoured due to the advantage of “maximum accumulation of unsaturated centres”, there is large amount of secondary orbital interaction and only a little structural deformation is needed to exploit them. The endo TS 7N is lower in energy than the exo TS 7X because 7X is destabilised by steric repulsion between the allyl (at the bottom phase) and methylene (at the top phase).

Product 3 vs 4: The dihydro derivative 3 is higher in energy than 4 by 4.5254 kcal/mol. This is mainly due to the Bend energy (higher bend energy might suggest a greater steric hindrance to hydrogenation). From this alone, one can suggest that the thermodynamic product dihydro 4 derivative is more stable than 3, therefore it is formed preferentially. This assertion is supported by experimental evidence. Literature reports that the first hydrogenation (-138.8 kJ/mol) takes place in the norbonene part of the molecule to form 4, then prolonged hydrogenation produces the tetrahydro-derivative (-109.5 kJ/mol).

Final Result: Dimerisation is kinetically controlled and hydrogenation is thermodynamically controlled.

6. Case Study 2: Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Pyridoxazepinone, is formed by the reaction of 2-chloronicotinic acid and L-prolinol). 2-chloronicotinic acid was activated by DCC (dicyclohexylcarbodiimde), 1-hydroxybenzotriazole, and N-methylmorpholine). An intermediate is cyclised by NaOH in an addition-elimination mechanism.

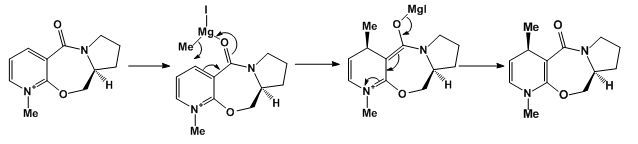
The methyl derivative, 5, of pyridoxazepinone undergoes a highly stereoselective and regioselective reaction with MeMgI to form 6 as the major product of the reaction and its regioisomer as the minor product with 19:1 regioisomer ratio and diastereomeric ratio 19:0 for 6.

6.1. COMPUTATIONAL ANALYSIS

Reaction 1: The structure of 5 generated from X-ray coordinates is similar to that obtained from molecular modelling. The construction of a CPK model of 5 revealed several interesting information about the diastereoselectivity of the reaction. First, the CPK model revealed an almost rigid 7-membered ring with only a few possible distortions (and/or conformers). A likely conformer is 5a, in this structure the carbonyl group is in the plane of the pyridine ring, this geometry is suitable for favourable n_N→π*_C=C (pp) interactions. Another conformer, 5b, has carbonyl group above the plane of the pyridine ring (and anti to H(18) of the chiral centre). With the CPK model, it is not possible to produce a conformation with the carbonyl group (only a slight deformation is possible) below the plane of the pyridine ring.

The results from MM2 analysis is given below;

Possible Structures of 5

Results	Structure
Stretch= 1.1870 Bend= 11.3873 Stretch-Bend= 0.0530 Torsion= 5.0851 Non-1,4 VDW= -2.0113 1,4 VDW= 11.8920 Charge/Dipole= 2.6982 Dipole/Dipole= -3.9687 Total Energy= 26.3228 kcal/mol	compound 5
Stretch= 0.8870 Bend= 6.7688 Stretch-Bend= 0.1193 Torsion= 9.5300 Non-1,4 VDW= -2.6703 1,4 VDW= 11.5240 Charge/Dipole= 3.2019 Dipole/Dipole= -3.8022 Total Energy= 25.5585 kcal/mol	comp 5
Stretch= 1.1825 Bend:= 11.5682 Stretch-Bend= 0.0519 Torsion= 4.8924 Non-1,4 VDW= -1.8967 1,4 VDW= 11.9458 Charge/Dipole= 2.6522 Dipole/Dipole:= -3.9894 Total Energy= 26.4070 kcal/mol	comp 5a

Compound 1 has C-C-C-O dihedral angle of 24.4, the dihedral angle of compound 2 is 41.5 and that of compound 3 is -21.4. In compound 3, the carbonyl is below the ring and this compound has the highest energy. Compound 2 has the lowest energy and the carbonyl group is well above the plane of the ring. It is compound two that reacts. The reaction proceeds via the chelation of the Grignard reagent to the carbonyl oxygen. The 'R' moiety is therefore delivered from the top phase i.e. above the plane of the pyridine thereby effecting a conjugate addition to the pyridine. A magnesium enolate is formed which is quenched with water.

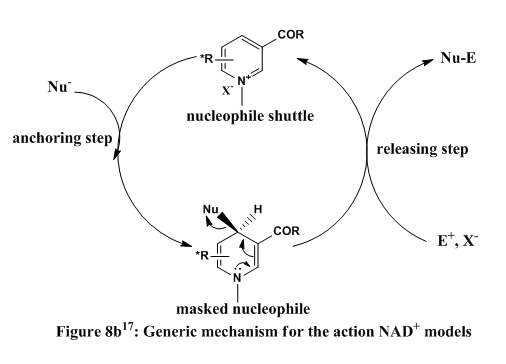
Reaction 2: Biological reactions are catalysed by enzymes and are highly stereospecific. One of such enzymes is NADH dehydrogenase which catalyses the the removal of hydrogen from substrates. Nicontinamide adenine dinucleotide (NAD) molecules are attached to this enzymes and they act as hydrogen transfer agents from substrate to substrate. NAD is presents as NAD⁺ is its oxidised form and it is reduced to NADH + H⁺.

An attempt to mimic such systems has led to the development of so-called NAD⁺ model. These models have been adapted for the stereospecific transfer of several groups like amides, enolates, cyanides (and other nucleophiles).

As displayed above, the main thrusts of biomimetic (inspired or derived from bio-systems) is the addition of the nucleophile to a pyridinium salt. In the spirit of its large marcomolecular equivalents, the pyridinium salt acts as a shuttle for nucleophile from one compound to another.

The delivery of nucleophiles to NAD⁺ is stereospecific, therefore the action of the 'masked nucleophile' that is formed on another compound is also stereospecific. Thus the question of how nucleophiles are delivered to NAD⁺ in a stereospecific fashion is important.

In this reaction, an amide transfer or 'anchoring' to the pyridinium reported by Leleu and co-workers¹⁷ is considered.

Scheme A: Diastereoselective formation of Chiral masked nuclephile. Photo taken from ref. 17. Scheme B: Reaction cycle for Diastereoselective formation of the Chiral masked nuclephile. Photo taken from ref. 17.

Scheme A	Scheme B

It is clear from experimental data that reaction is diastereoselective (proven by spatial hydrogen symmetry, Nuclear Overhauser effect). Experimental data shows that the atropenantioselective amidification of ethanoylchloride is 90% stereospecific. The reason for this is the chiral axis of the C3-C=O bond governs the stereoselectivity of the addition. The fact that the C=O group is above the plane of the carbonyl ring means that nucleophilic reagents are delivered from the top phase. This is similar to reaction 1. The reagent must be able to chelate or coordinate to the C=O oxygen, reagents that are unable to do this attack from the bottom phase.

The structure reveals a chiral C3-C=O element in agreement with literature. This atropisomerism is induced by the adjacent chiral carbon bearing the methyl group.

7. Case Study 3: Stereochemistry and Reactivity of an intermediate in the synthesis of Taxol

Taxol or Paclitaxel is an anticancer drug. Its mechanism of action is to prevent the assembly of spindle fibres and thereby preventing cell division. Cell arrested at this stage undergo cell death. Intermediates, 9 and 10 below show that 10 is far more stable by a quite a margin.

Compound 9	Compound 10
comp 9	comp 10
Total energy = 61.2304 kcal/mol	Total energy = 49.9757 kcal/mol

MM2 analysis revealed that compound 10 is far more stable. This difference in energy is 11.2547 kcal/mol. This difference is large enough to effect the isomerisation of 9 to 10 on standing. This alkene is hyperstable due eclipsed interaction between the vicinal transannular hydrogens. The slowness of hydrogenation is due to the presence of an intermediate in the hydrogenation pathway, that eclipses the added hydrogens.

8. Case Study 4: Regioselective addition of Dichlorocarbene

Ref. 18: B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447

Carbenes are very reactive, electron deficient species with six electrons. In their quest to gain a stable octet configuration, they react with several electron rich compounds. Carbene insert to C=C alkene bonds as seen in this case study. Also the they are able to insert into C-C and C-H single bonds.

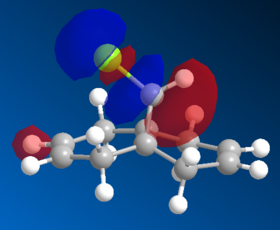
The addition of carbene to 12 is a peculiar reaction. The addition occurs from the bottom phase as expected due to the steric bulk of Cl atom. However a second observation is that the carbene adds to the alkene that is endo to the Cl atom.

The valence electron molecular wavefunction at MOPAC/PM6 level

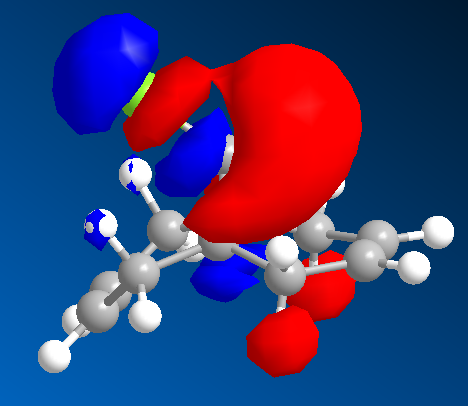
HOMO	HOMO-1	LUMO	LUMO+1	LUMO+2	LUMO+2 (PM3)

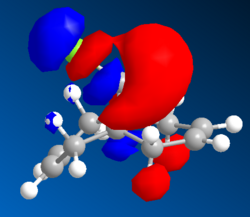
The MO wavefunctions reveal that there is antipleriplanar interactions between the C-Cl σ* (LUMO+2, PM3)and the exo π orbital (HOMO-1, PM6) relative to the endo π orbital, rendering the endo π orbital more nucleophilic towards the carbene.

8.1. Vibrational Spectra

Characteristic vibrational modes

Compound 12	Hydro Product
Description	Description

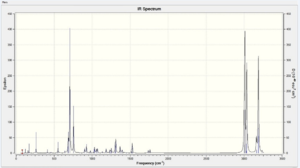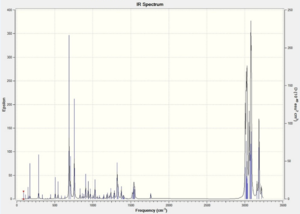For compound 12, the C=C stretching frequencies due to the exo and endo C=C bonds were observed at 1739 and 1761 cm^-1. For the hydro-product the C=C stretching frequency was observed at 1762 cm^-1. These numbers are higher than the normal C=C stretching frequency of 1690 cm^-1. Therefore the effect of the C-Cl bond is the C=C bond shorter.

9. Mini-project: The 2:1 adduct of cyclopentadiene and p-benzoquinone

The step formation of the 2:1 adduct is step-wise, first a 1:1 adduct is formed, for the reason a cursory look at the 1:1 adduct is needed.

Cyclopentadiene reacts with p-benzoquinone to give a 1:1 adduct, This synthesis was first reported by W. Albrecht in 1906. Historically, several structures have benn attributed to the 1:1 adduct, first the reaction was taught to proceed via a Michael addition reaction to produce 1. Then a 1,2 cycloaddition product, 2, was suggested. Finally, the research done by Diels and Alder showed that the 1:1 adduct was in fact a 1,4-adiition product, 3. The main product of the reaction was 4, a cis-endo product. this was deduced by the observation of 5 (a pentacyclic isomer, cis-exo cannot) bend to cyclise). In solution the 1:1 adduct adopts the open geometry of 6. P. Yates and co-workers reported the previously unseen cis-exo isomer by the boiling the relevant 2:1 adduct with p-benzoquinone in xylene mixture for 20min.<

NOT BH3 BUT RXN SCHEME FOR PREVIOUS PARAGRAPH

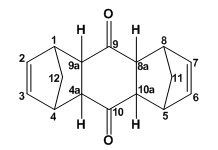
In the formation of the 2:1 adduct, two mole eq. of cyclopentadiene is used. The generic structure of the adduct is 7. Most cycloadditions proceed via cis-addition as does this reaction. There are six possible stereoisomers for 7. Their formation is rationalised as follow: First a reaction between cyclopentadiene and p-benzoquinone occurs to give the 1:1 adduct. For now we consider all possible products. There is the possibility of forming the cis-exo and cis-endo products (cis cycloaddition is due to orbital symmetry, also note that cis in 1:1 adduct defines the geometry of the two fused hydrogens), 8 and 9. When another cyclopentadiene molecule is reacts with the 1:1 adduct, there is a possibility (for the sake of argument, not experimental results!) of forming six different isomers depending on the geometry of the second fused H's and the carbon bridge heads.

MM2 ANALYSIS OF COMPOUNDS 10-15

	Compound 10	Compound 11	Compound 12	Compound 13	Compound 14	Compound 15
Structure	Endo-syn-Endo	Endo-anti-endo	Endo-syn-exo	Endo-anti-exo	Exo-anti-exo	Exo-syn-exo
Data	Stretch= 2.1083 Bend= 34.7369 Stretch-Bend= -1.2985 Torsion= 16.1868 Non-1,4 VDW= -4.4834 1,4 VDW= 10.0993 Dipole/Dipole= 3.9794 Total Energy= 61.3288 kcal/mol	Stretch= 2.0551 Bend= 35.7318 Stretch-Bend= -1.2815 Torsion= 19.4658 Non-1,4 VDW= -4.5727 1,4 VDW= 10.3523 Dipole/Dipole= 3.2432 Total Energy= 64.9940 kcal/mol	Stretch= 2.1794 Bend= 34.3509 Stretch-Bend= -1.3067 Torsion= 17.1641 Non-1,4 VDW= -3.9982 1,4 VDW= 10.2964 Dipole/Dipole= 3.7379 Total Energy= 62.4238 kcal/mol	Stretch= 2.1289 Bend= 35.7447 Stretch-Bend= -1.2703 Torsion:= 20.5812 Non-1,4 VDW= -4.1828 1,4 VDW= 10.5011 Dipole/Dipole= 3.1842 Total Energy:= 66.6869 kcal/mol	Stretch= 2.2179 Bend= 35.2315 Stretch-Bend= -1.2923 Torsion= 21.5639 Non-1,4 VDW= -3.6618 1,4 VDW= 10.9029 Dipole/Dipole:= 3.7228 Total Energy= 68.6848 kcal/mol	Stretch= 2.2437 Bend= 34.0681 Stretch-Bend= -1.3401 Torsion= 17.9354 Non-1,4 VDW= -3.8495 1,4 VDW= 10.6173 Dipole/Dipole= 3.5094 Total Energy= 63.1843 kcal/mol

X-ray crystallography data showed that the product of the reaction of the endo 1:1 adduct with cyclopentadiene was the endo-anti-endo isomer, 11 (mp 155^oC). Literature also reports the isomerization of 11 in alkali to the endo-syn-exo structure, 12 (mp 186^oC). Synthesis of 10 (mp 184^oC) has also been reported. Reasearch done by Yates et al produced 13 (mp 153-154^oC) and 14 (mp 163-164^oC) by the heating 11 in xylene in a sealed tube at 120^oC to produce a mixture of 11, 13, 14.

The isomerization of 11 to 12 under basic conditions is not surprising because steric energy decreases by 2.5702 kcal/mol. Two different mechanisms have been proposed for the interconversion of exo- and endo- forms; these are enolisation and dissociation-recombination. For 11 to 12 transformation, the kinetic endo-anti-endo product is transformed in the thermodynamic product by either of the two mechanisms.

This shows the interconversion of 11 to 12 via an enolisation mechanism, a thermal interconversion is also possible. Also the thermal interconversion of 11 to 13 and 14 (derived mechanism, c.f. ref 15) is presented, and again a more intuitive enolisation mechanism can be presented.

The interconversion of 11 to 13 and 14 seems unusual because the energy goes from 64.9940 kcal/mol to 66.6869 kcal/mol and 68.6848 kcal/mol i.e. the less stable products are formed under thermodynamic conditions! However experimental observation resolves this dilemma. In the 'normal interconversion' to 12, Yates et al reports the 'isomerisation' of 11 to 12, with little side products. However for the less stable 13 and 14, an equilibrium mixture of 11, 13, 14, with the equilibrium towards 11 (position of equilibrium was not established).

10.1. Vibrational Spectra of 13 and 14

Vibrational data at the b3lyp/6-31G(d) level

Compound	Wavenumber (expt.)/ cm-1	Wavenumber (ref. 15)/ cm-1	Vibrational mode
13	1648.63	1686
13	1648.66	------
14	1648.25	1681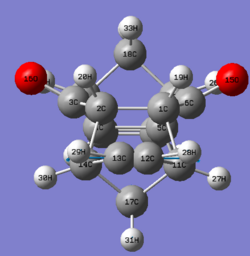
14	1653.55	1687

The peaks obtained from these calculations agree with experimental value. The carbonyl stretching modes are presented below.

Vibrational data at the b3lyp/6-31G(d) level

Compound	Wavenumber (expt.)/ cm-1	Vibrational mode
13	1783.77
13	1787.63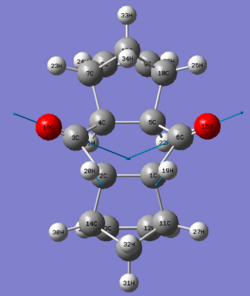
14	1783.60
14	1787.79

These wave-numbers are characteristic of carbonyl stretching frequency.

IR Spectrum from b3lyp/6-31G(d) level calculations

13	14

10.2. ¹³C NMR of 13 and 14

Carbon atoms	Compound 10	Compound 11	Compound 12	Compound 13	Compound 14
1,4	43.9	48.1	43.4	47.6	47.8
5,8	43.9	48.1	43.9	48.7	47.8
2,3	137	136.3	137.2	135.9	137.6
6,7	137	136.2	137.5	137.3	137.6
4a,9a	54.0	53.1	52.9	52.4	53.2
8a,10a	54.0	53.1	55.4	53.6	53.2
9,10	209.8	212.5	210.4	211.9	211.9
11	47.0	49.5	47.6	50.4	45.5
12	47.0	49.5	47.4	46.5	45.5

Double values indicate equivalent protons.

Calculated value for ¹³C nmr spectra for 10-14

Carbon atoms	Compound 10	Compound 11	Compound 12	Compound 13	Compound 14
1,4	46.36	47.7	46.3	48.1	49.4
5,8	46.36	50.5	46.4	50.6	47.2
2,3	137.6	136.4	138.0	135.2	140.9
6,7	137.6	136.2	137.1	139.1	138.9
4a,9a	55.7	59.6	54.6	53.8	56.2
8a,10a	55.7	56.2	56.4	55.4	53.2
9,10	205.5	207.9	205	206.8	206.5
11	54.7	55.6	53.9	60	53.5
12	54.7	54.7	53.6	55.4	54

The calculated nmr spectrum agree well with literature with some discrepancies in the absolute values. The startling observation is that it discriminates between the symmetry of the different isomer. The data shows that the spectrum of endo-exo isomer are complex than those of the endo isomer due to lower symmetry.

Thus, quantum mechanical calculations can differentiate isomer with very low energy, and can predict their spectra. As to prediction of the product of reaction, high level TS calculation is needed.

10. Conclusion

Computational analysis is needed indispensable in the age of precise thinking and experimentation.