Rep:Mod:og31

Transition States and Reactivity

Introduction

The potential energy surface (PES) of a molecule is a graph created from all the possible structures that a particular molecule could have. The hills have high energy and so the molecule is likely not to stay in that conformation whereas the troughs have low energy so those structures are more stable. A transition state is a point on the PES that has a the highest energy along a reaction pathway and a minimum has the lowest energy. The differential of a transition state and minimum is 0 but the second differential is negative for a transition state and positive for minimum; this describes the curvature. By performing a frequency calculation, it is possible to tell if the structure is at a transition state because the calculation will have one negative frequency. The calculations performed were achieved using density-functional theory (DTF) and PM6 methods.

Nf710 (talk) 22:26, 17 November 2016 (UTC) It is an imaginary frequency, you could have given the relationship between the negative curvature and the imaginary frequency.

Reaction of Butadiene with Ethylene

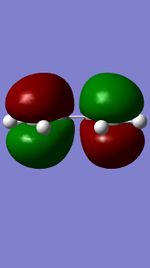
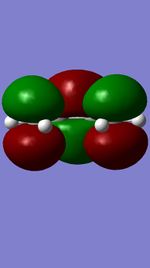
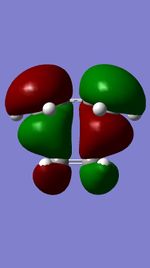
The Diels-Alder reaction between butadiene and ethylene was investigated. The frontier orbital MO diagram of the transition state between the two reactants can be seen in Figure 1 and the HOMO and LUMO of the reactants can be seen in Figures 2,3,4 and 5. These orbitals can be combined in the way shown in Figure 1 to produce the MOs seen in Figures 6,7,8 and 9. The orbitals can only combine if they have the same symmetry; an ungerade-ungerade interaction and gerade-gerade interaction will have an orbital overlap of non-zero. An example of a non-zero orbital overlap is when the HOMO of butadiene combines with the LUMO of ethylene, they both have ungerade symmetry. If two MOs with different symmetry try to combine the orbital overlap will be 0 i.e. non bonding.

Figure 1: MO Diagram.

Figure 2: HOMO of Ethene.	Figure 3: LUMO of Ethene.	Figure 4: HOMO of Butadiene.	Figure 5: LUMO of Butadiene
Figure 6: MO 1.	Figure 7: MO 2.	Figure 8: MO 3.	Figure 9: MO 4.

Figure 10: Diels-Alder Transition State.

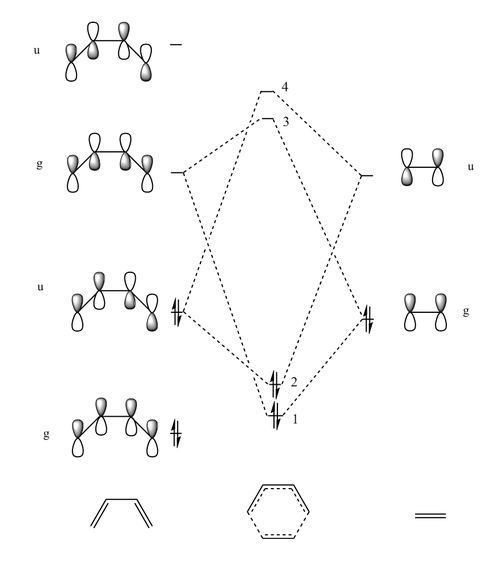
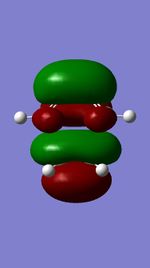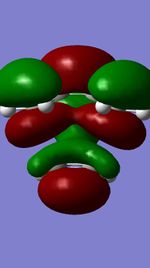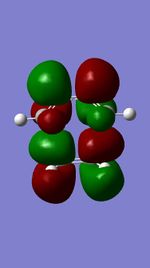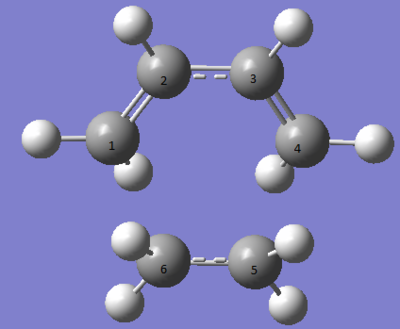
Table 1 shows that all of the bonds in the reactants, apart from the C-C bond in butadiene, get longer as the transition state is formed. This is expected because the double bonds are breaking and so they become more like single bonds which are longer, and the single bond in butadiene becomes a double bond so it gets shorter. Most of bond lengths in the transition state are between the lengths of an sp3 and sp2 carbon. The calculated data matches the data that Goldstein et. al. found. The Van Der Waals radius for a carbon atom is 170Å and the bond length of C4-C5 is smaller than that and can therefore be called a partial bond.

Table 1: C-C bond lengths

		Bond Lengths (Å)	Ref
Reactants	Ethene	1.33
	Butadiene C-C	1.47
	Butadiene C=C	1.34
Transition State	C1-C2	1.38	1.383
	C2-C3	1.41	1.407
	C3-C4	1.38	1.383
	C4-C5	2.27	2.273
	C5-C6	1.39
	C6-C1	2.27	2.273
Products	C1-C2	1.51
	C2-C3	1.32
	C3-C4	1.51
	C4-C5	1.55
	C5-C6	1.56
	C6-C1	1.55

GIF 1 shows the synchronous formation of the two bonds.

GIF 1: Transition state reaction path

Nf710 (talk) 22:31, 17 November 2016 (UTC) Everything was well done in this section

Reaction of Benzoquinone with Cyclopentadiene

The next reaction that was computed was the Diels-Alder reaction between benzoquinone and cyclopentadiene. This reaction can yield an exo and an endo product and the energies of the reaction are tabulated in Table 2. The data shows that the energies of the products in both cases are more positive than the reactants which suggests that the reaction is endothermic. The thermodynamic product has the lowest Gibbs free energy and the kinetic product has the lowest activation barrier therefore the endo product is both the thermodynamic and the kinetic product which is confirmed by Tormena et. al.

Table 2: Thermodynamic Energies for Benzoquinone and Cyclopentadiene

		Energy (kJ/mol)
Reactants	Cyclopentadiene	-509438.3563
	Benzoquinone	-1001357.467
exo	Transition state	-1510663.737
	Product	-1510782.895
	Activation	132.08629
	Gibbs	12.92796
endo	Transition state	-1510670.426
	Product	-1510783.837
	Activation	125.396515
	Gibbs	11.9854084

Figure 11: HOMO of exo Transition State.	Figure 12: LUMO of exo Transition State.
Figure 13: HOMO of endo Transition State.	Figure 14: LUMO of endo Transition State.

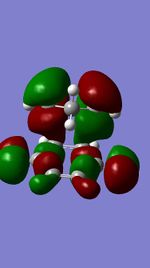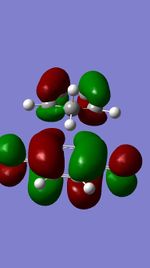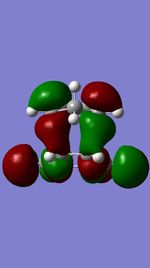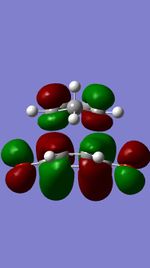(At this angle it can be difficult to see what the difference is between the endo and exo TSs Tam10 (talk) 12:53, 9 November 2016 (UTC))

Figures 11,12,13, and 14 show the HOMOs and LUMOs of the exo and endo transition states. The nodes in the LUMOs and the orbital overlap in the HOMOs can be clearly seen between the two molecules.

Nf710 (talk) 22:48, 17 November 2016 (UTC) Nice uses of literature. 2 point you calculated your reactants from infinite separation, it should be from the first point on the irc optimized. you also didnt give any reason as to why the endo is the kinetic and thermo.

Diels-Alder vs Cheletropic

Xylylene can undergo a Diels-Alder reaction with sulphur dioxide to afford the exo and endo product however it can also undergo a cheletropic reaction to produce a different product. Table 3 shows the energies that have be computed for these reactions. Between the exo and endo products, the endo is the kinetic product and the exo is the thermodynamic product. The Cheletropic product is the most stable how it has the largest activation energy so it will only form under high temperatures. At room temperature, the Diels-Alder reaction will be more frequent and there will be be a mix of the endo and exo. It is likely that the endo product will be the major product because the energy difference of the reaction between the endo and exo is very small compared to the activation energy as seen in Figure 15. The IRC of the reactions can be seen in GIFs 2,3, and 4.

Table 3: Thermodynamic Energies for Xylylene and Sulphur Dioxide

		Energy (kJ/mol)
Reactants	Xylylene	467.630466
	Sulphur Dioxide	-311.4210807
exo	Transition state	241.748182
	Product	56.3301068
	Activation	85.538797
	Gibbs	-99.87927861
endo	Transition state	237.765298
	Product	56.9838563
	Activation	81.5559127
	Gibbs	-99.22552906
Cheletropic	Transition state	339.534937
	Product	0.005251
	Activation	183.325551
	Gibbs	-156.2146364

Figure 15: Reaction Profile.

GIF 2: IRC of Cheletropic Product.	GIF 3: IRC of endo Product.
GIF 4: IRC of exo Product.

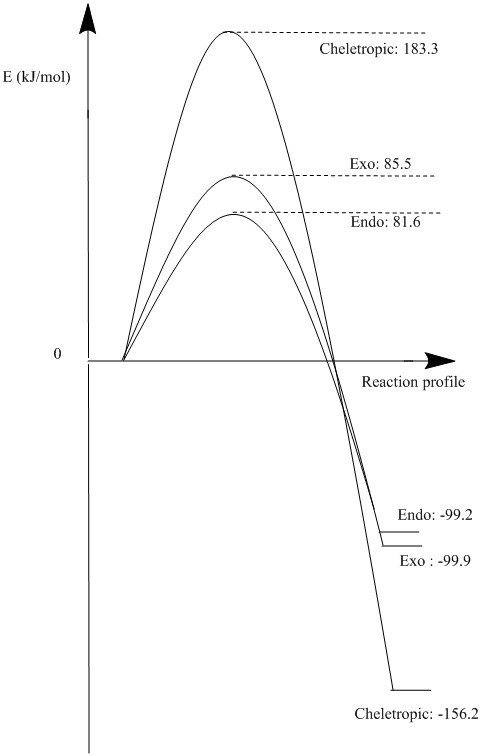
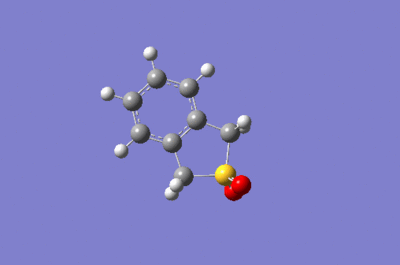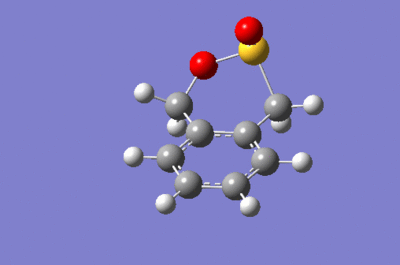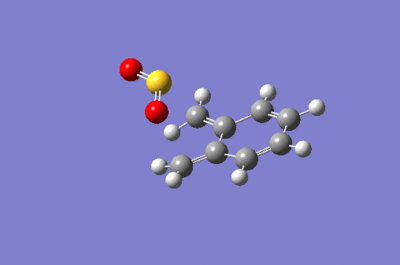(What about the thermodynamic instability of xylylene? Tam10 (talk) 12:53, 9 November 2016 (UTC))

Conclusion

The exo and endo products of Diels-Alder reaction have different activation and Gibbs free energies and so there will be a major and a minor product when it is carried out experimentally. The data calculated from GaussView has been shown to correlate with the literature and give accurate bond lengths and energies.