Rep:Mod:oIEETToE
NH3
| Summary | |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776873 au |
| RMS gradient | 0.05399560 au |
| Point group | C3V |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
N-H bond distance: 1.01798 Å
H-N-H bond angle: 105.741°
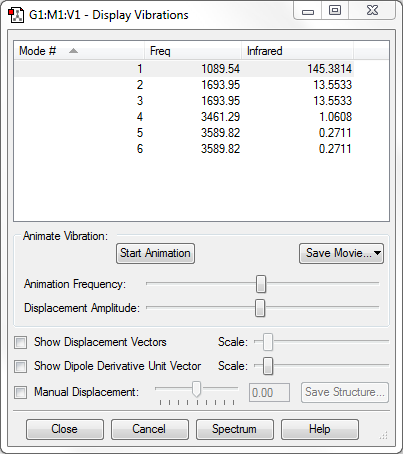
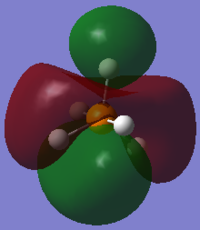
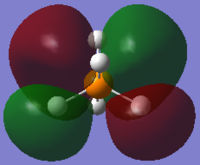
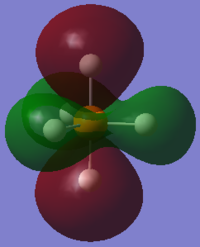
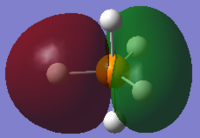
From the 3N-6 rule for non-linear molecules, we would expect 6 modes of vibration, which can be seen in the image above.
Modes 2 and 3 are degenerate, as are modes 4 and 5.
Modes 1, 2 and 3 are bending vibrations while modes 4, 5 and 6 are stretching vibrations.
Mode 4 is highly symmetric.
Mode 1 may be called the 'umbrella' mode as it slightly resembles a flipping or opening and closing umbrella.
We would expect 4 bands in the IR spectrum for gaseous NH3 as it appears that every mode has a change in dipole moment, although 2 of them would be quite weak.
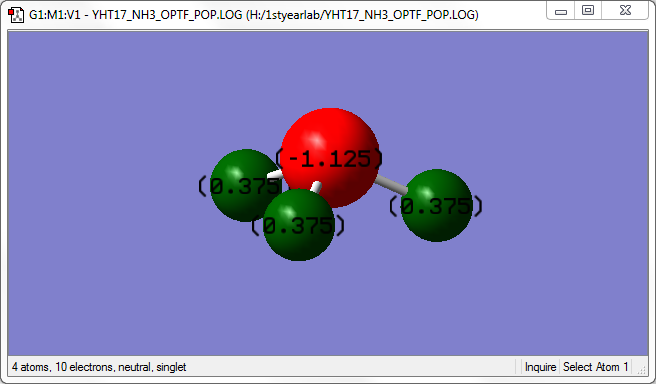
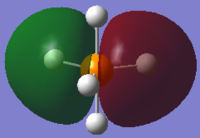
The image above shows the charges on each atom in NH3.
It is expected that N would have negative charge and H would have positive charge because N as a higher electronegativity than H.
The optimisation file for NH3 is linked to here
N2
| Summary | |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -109.52412868 au |
| RMS gradient | 0.00000060 au |
| Point group | D∞H |
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
There is one mode of vibration at a frequency of 2457.33 (IR inactive).
The optimisation file for N2 is linked to here
H2
| Summary | |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -1.17853936 au |
| RMS gradient | 0.00000017 au |
| Point group | D∞H |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
There is one mode of vibration at a frequency of 4465.68 (IR inactive).
The optimisation file for H2 is linked to here
N2 + 3H2 -> 2NH3
| Energies | |
|---|---|
| E(NH3) | -56.55776873 au |
| 2×E(NH3) | -113.11553746 au |
| E(N2) | -109.52412868 au |
| E(H2) | -1.17853936 au |
| 3×E(H2) | -3.53561808 au |
| ΔE = 2×E(NH3)-(E(N2)+3×E(H2)) | -0.0557907 au = -146.48 kJ mol-1 |
This shows that the ammonia product is more stable than the gaseous reactants, which means the reaction is exothermic.
[AlBr4]-
| Summary | |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -10529.67123680 au |
| RMS gradient | 0.00000140 au |
| Point group | Td |
Item Value Threshold Converged? Maximum Force 0.000003 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000021 0.001800 YES RMS Displacement 0.000011 0.001200 YES
Al-Br bond distance: 2.32607 Å
Br-Al-Br bond angle: 109.471°
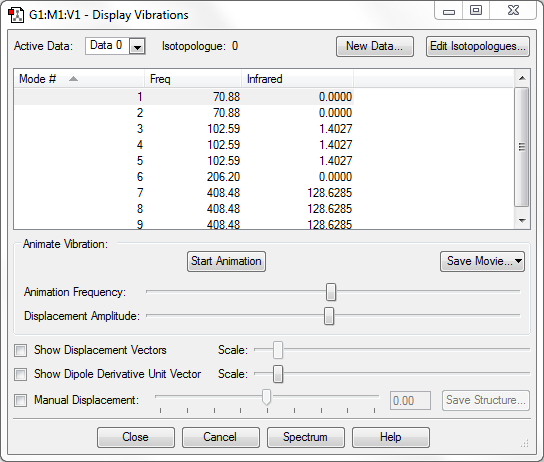
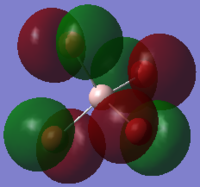
From the 3N-6 rule for non-linear molecules, we would expect 9 modes of vibration, which can be seen in the image above.
Modes 1 and 2 are degenerate, as are modes 3 to 5 and modes 7 to 9.
Because Br is not light compared to Al, only one mode, the highly symmetric mode 6, is a stretching vibration.
We would expect 2 bands in the IR spectrum for gaseous [AlBr4]- as there are two different frequencies at which there is IR absorbance (the others are IR inactive because there is no change in dipole moment). One of them would be quite weak.
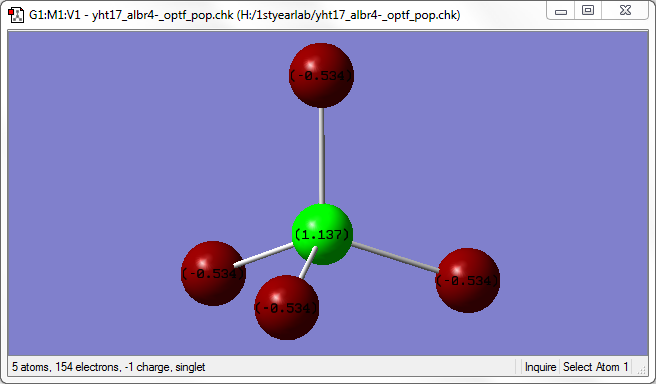
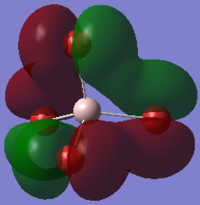
The image above shows the charges on each atom in [AlBr4]-.
It is expected that Br would have a lower charge than Al because Br as a higher electronegativity than Al.
| Molecular Orbitals | |||
|---|---|---|---|
| 78 (LUMO) | 
|
0.15203 au | This is the LUMO. It appears to be an antibonding MO formed by the 3S orbital on the Al and 3p orbitals on the Br. It is the antibonding equivalent of MO 66. The back of the p orbitals are exposed, but are unlikely to accept electrons because the molecule has a negative charge and the Br have further negative charge due to its higher electronegativity compared to Al. |
| 75-77 (HOMO) | 
|
-0.12452 au | These three degenerate MOs are the HOMO. They are identical in shape and differ only by orientation. They appear to be non-bonding MOs formed by a 3p orbital on each Br atom. The p orbitals are quite exposed so electrons may be given away, possibly with the loss of Br-. |
| 70 | _-0.15118.PNG)
|
-0.15118 au | This MO is close in energy to the HOMO. It appears to be a bonding MO formed by a 3p orbital on each Br atom. Because its energy is close to the HOMO, it is possible that electrons can be taken from this MO in a reaction. |
| 66 | 
|
-0.27588 au | This appears to be a bonding MO formed by the 3S orbital on the Al and 3p orbitals on the Br. It is the bonding equivalent of the LUMO (MO 78). It is probably too deep in energy to be involved in reactions. |
| 62 | 
|
-0.60894 au | This appears to be a bonding MO formed by 3s orbitals on the Al and Br. It is too deep in energy to be involved in reactions. |
The optimisation file for [AlBr4]- is linked to here
PH5
As we learn in the Periodicity course, this compound does not exist due to weak bonding between P and H caused by the size mismatch between the n=3 orbitals on the P and the 1s orbitals on the H. Therefore, all the information in this section is about a purely theoretical molecule and has little use.
| Summary | |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -344.25491049 au |
| RMS gradient | 0.00000471 au |
| Point group | D3h |
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000055 0.001800 YES RMS Displacement 0.000022 0.001200 YES
P-H(axial) bond distance: 1.48687 Å
P-H(equatorial) bond distance: 1.43316 Å
H(axial)-P-H(axial) bond angle: 180.000°
H(axial)-P-H(equatorial) bond angle: 90.000°
H(equatorial)-P-H(equatorial) bond angle: 120.000°
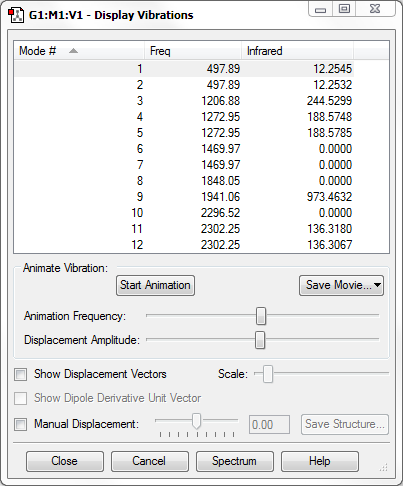
From the 3N-6 rule for non-linear molecules, we would expect 12 modes of vibration, which can be seen in the image above.
Modes 1 and 2 are degenerate, as are modes 4 and 5, modes 6 and 7 and modes 11 and 12.
Modes 1 to 7 may be considered bending vibrations while modes 8 to 12 may be considered stretching vibrations.
Mode 10 is highly symmetric.
We would expect 5 bands in the IR spectrum for gaseous PH5 as there are five different frequencies at which there is IR absorbance (the others are IR inactive because there is no change in dipole moment). One of them would be quite weak.
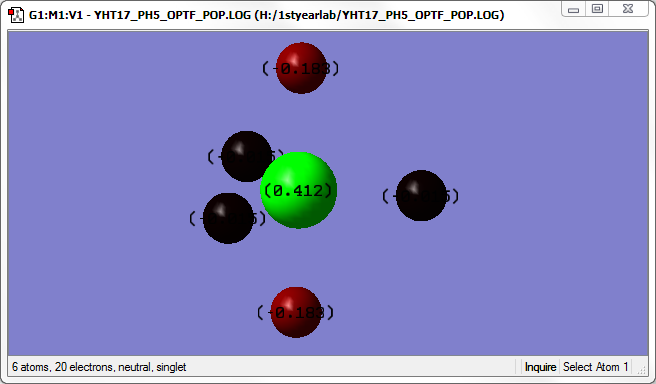
The image above shows the charges on each atom in PH5. The charge on each of the equatorial H atoms is not very visible, but they are -0.015.
P and H have similar electronegativity, so we would expect the charges to be quite balanced. However, there is some negative charge on the axial H atoms, perhaps so that the electrons can be further apart.
| Molecular Orbitals | |||
|---|---|---|---|
| 12 (LUMO) | _LUMO_0.04278.PNG)
|
0.04278 au | The LUMO has two degenerate molecular orbitals. This is one of them. It appears to be an antibonding MO formed by a 3p orbital on the P and 1s orbitals on the three equatorial H. It is the antibonding equivalent of MO 8. |
| 11 (LUMO) | _LUMO_0.04278.PNG)
|
The LUMO has two degenerate molecular orbitals. This is one of them. It appears to be an antibonding MO formed by a 3p orbital on the P and 1s orbitals on two of the three equatorial H. It is the antibonding equivalent of MO 7. | |
| 10 (HOMO) | 
|
-0.21463 au | This is the HOMO. It appears to be a bonding MO formed by the 3dz2 orbital on the P and 1s orbitals on all five H. |
| 8 | _-0.42682.PNG)
|
-0.42682 au | This appears to be a bonding MO formed by a 3p orbital on the P and 1s orbitals on the three equatorial H. It is the bonding equivalent of MO 12. |
| 7 | _-0.42682.PNG)
|
This appears to be a bonding MO formed by a 3p orbital on the P and 1s orbitals on two of the the three equatorial H. It is the bonding equivalent of MO 11. | |
The optimisation file for PH5 is linked to here