Rep:Mod:nsolomon1


Welcome to this threefold computational experiment:
In Part (i) Molecular Mechanics (MM) will be used to optimise the geometries and hence the energies of various molecules to produce energy minimum conformers. MM is a classical method of modelling the steric energy of a system by summing up all the various contributions (such as stretching, bending, Van der Waal, torsion and H-bonding terms) to the total energy to determine the strain, steric hindrance or lowest energy conformer in a system. Allinger MM2 models through ChemBioDraw 3D Ultra 12.0 will be used to compute the relative energies of different isomers which will then be rationalised by considering the various contributions to the total energy. This will enable us to predict the most favourable geometries and regioselectivity observed experimentally.
In Part (ii) we will make the transition to a quantum mechanical treatment of the system and adopting a semi-empirical Molecular Orbital Theory approach to compute electronic aspects of reactivity. The electrons orbiting atoms are now considered and their effect on bonds and spectroscopic properties analysed. This is achieved by generating the electronic wave functions using the MOPAC/PM6 method through ChemDrawBio3D ultra 12.0.
In Part (iii) we will use Density Functional Theory (DFT) to compute spectroscopic properties of two isomers in the literature and verify them against the experimental results. DFT is a quantum mechanical modelling method used to predict the properties of many body systems using functionals, i.e. in this case spatially dependent electron density. In particular we will focus of verifying the enantiomer claimed to be formed for a indatraline precursor.
Part(i) Modelling using Molecular Mechanics
1.1 The Hydrogenation of Cyclopentadiene Dimer
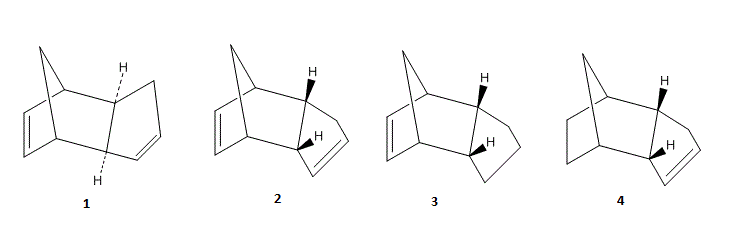
Below are the exo- (1) and endo- (2) products from the dimerisation of cycloentadiene. Products (3) and (4) are as a result of the hydrogenation of (2).
Computing the energies using the MM2 force field we observe the following contributions to the steric energy:
Energy contributions (kJ/mol) to the exo and endo isomers and the hydrogenated endo isomer
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In a classical sense, comparing 1 (exo-) and 2 (-endo) we can see that molecule 1 is the more energetically stable conformer, deeming it the thermodynamic product. This is consistent with experimental results where under non equilibrating conditions we find that the endo- product is formed preferentially over the exo- product, suggesting it is the higher energy kinetic product. Comparing the energy contributions to the overall steric energy for molecules 1 and 2 we see that the greatest difference lies in the dihedral term describing the torsion around the bond. For molecule 1 we compute E (torsion) = 32.1 kJmol-1 and for molecule 2 E (torsion) = 39.8kJmol-1. Using different software would enable us to pin point which bond(s) are responsible for this difference; something beyond the scope of ChemBioDraw 3D.
However what MM cannot rationalise is that at high temperatures, where we would expect the thermodynamic product to dominate [1], the endo- product is still favourable. We should consider the orbital and geometrical alignments of the transition states to explain this. The reaction involves a concerted [4+2] cycloaddtion reaction. The dimerisation may occur via two distinct approaches:
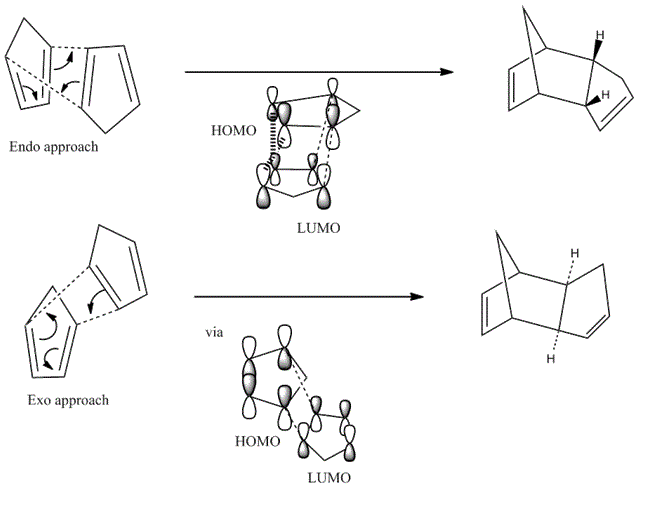
Taking a semi empirical molecular orbital approach, with the endo- approach we observe a primary orbital overlap (dashed line) and an energetically favourable secondary orbital overlap (hashed line) compared to the exo- approach where only a primary overlap is observed. This renders the endo- approach kinetically favourable giving the kinetic product. This is the basis on the Woodward-Hoffmann rules[2].
For the hydrogenated molecules 3 and 4 we see E (total) = 149.3kJmol-1 or 130.4kJmol-1 respectively illustrating enough energy difference to render 3 and 4 the effective “kinetic” and “thermodynamic” products respectively. We observe that the largest differences arise in the bending term E (bend) = 83.3kJmol-1 or 14.5kJmol-1 respectively. We may rationalise this by considering the location of the double bond. In 3 the double bond is preventing any alleviation of strain in the bridgeheaded 5 membered ring, whereas in 4 the double bond is in a position that does not affect the natural geometry of an “endo-like” product. This accounts for 4 being the “thermodynamic product” as this bridgehead strain is alleviated upon hydrogenation.
1.2 Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
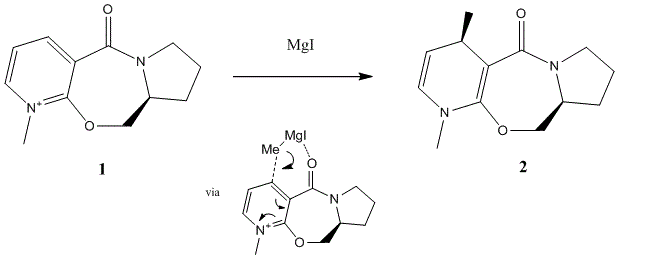
The prolinol derivative shown (1) is an optically active compound which may be easily alkylated in the 4-postion with the Grignard reagent, MgI. We will now investigate the stereochemistry of the product using MM2 energy optimisations. The following alterations i), ii) and iii) refer to the following reference conformation (a) which was simply obtained by drawing (1) and applying a minimisation - i) Conformer (b) was obtained by inverting the oxygen in the 7 membered ring, ii) conformer (c) obtained by inverting carbons 2,3 on the 5-membered N-ring and iii) conformer (d) by applying i) and ii) simultaneously.
Reaction scheme:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The first thing to notice is that all the conformations show a positive (O)=C-C-C-H dihedral angle, indicating that the oxygen is orientated upwards with respect to the plane of the page; even if this is only by ca 9°. A paper by Shultz et. al [3] suggests that the lowest energy conformation of molecule (1) is indeed that with an oxygen out of plane with the aromatic ring. We may therefore rationalise the absolute stereochemistry of (2) by considering the coordination of the electropositive magnesium from the Grignard, leading to an energetically favourable 6-membered transition state above the plane of the aromatic ring. Conformers a and b appear to be energetically very similar in terms of the various contributions suggesting that inversion of the 7-membered ring oxygen has little effect on the overall energy. Conformers b and d appear very comparable except that conformer d has a much lower torsion energy (in relation to all compounds) rendering it the lowest energy conformation by 4-7 kJmol-1; c.f. variation principle.
Interestingly if we consider the lowest energy conformation of the enantiomer of molecule (1) we see a dihedral angle of ca -8.2° which would lead us to predict the anti alkylated product. Note an attempt was made to introduce the Grignard into the minimisation but as Magnesium is not included in the ChemDrawaBio 3D database it is neglected from the calculation. An attempt was made to use an electropositive analogue such as CF4 but no effect was observed confirming that the molecular mechanics had no “chemical intuition”.
Secondly we will consider the derivatisation of a 7-membered pyridinium ring (3) with aniline to give (4).
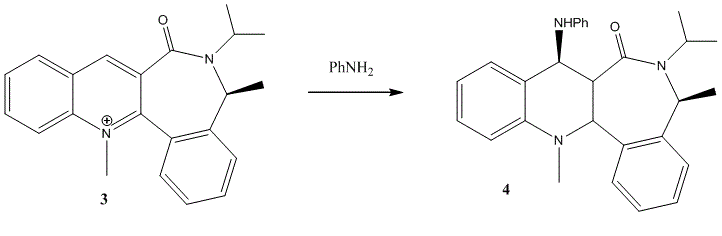
Prediction: the stereocontrol may be predicted by considering the absence of a coordinating cation such as magnesium in the previous example. The stereochemistry is purely controlled on the basis of approach from the the least hindered/repulsive face.
Indeed this is what is observed. Energy minimisation of the conformer shown in (3) results in the oxygen directed face down with a the carbonyl oxygen (O)=C-C-C-O dihedral angle of -20.2° as shown in conformer (e). Regioselectively, the aniline therefore approaches from the opposite side to which the oxygen is directed (perhaps due to lone pair-lone pair repulsion) to give the stereochemistry shown in (4). The other conformer considered is (f) where the phenyl fused to the 7-membered ring adjacent to the methyl is (conversely to (e)) directed upwards. This illustrates the negative dihedral angle between the carbonyl and the aromatic ring and also in theory gives the stereochemistry observed.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Clearly conformer e is the most energetically stable by 71 kJmol-1 deeming f highly unfavourable. This may be attributed to a lower steric clash between the aforementioned phenyl and methyl groups affecting most of the various contributions.
Improvements
We may improve our simple model by attempting to incorporate the effect of solvents on the system. Perhaps different solvents will influence the stereochemistry of the product. However this is beyond the scope of ChemDrawBio 3D Ultra and a quantum mechanical molecular reaction dynamics approach in which the transition state is considered would have to be employed. This leads onto more sophisticated quantum mechanical models which consider the electron density on each atom such as the semi-empirical MO theory MOPAC and Gaussian Density Functional Theory methods. These methods would allow us to focus on the plausibility of the proposed coordination in the prolinol reaction or the lone pair repulsion in the NAD+ analogue reaction.
1.3 Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol.
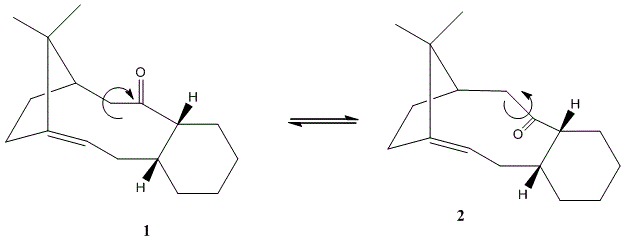
Now we will consider key intermediates (1) and (2) of Taxol, an important anti-cancer drug. On standing the molecule exhibits anisotropism and naturally isomerises to the most stable form. MM2 will once again be used to determine, sterically, which is the most stable isomer.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The MM2 minimisation calculation deems structure (2), the chair isomer, the most energetically favourable structure by 64 kJmol-1; presumably at room temperature (kT=2.5kJmol-1) the equilibrium above would lie to the right and only when T ~ 7900K would (1) be observed . We see the greatest differences lie with the bending energies where a difference of 41 kJmol-1 is found. By visual inspection, if the 3D structure is considered we can see that for molecule (2) there is much more open structure and less of a steric clash between the two ends of the molecule than for (1). This is in line with the literature[4]. Also if we consider the sp2 hybridised carbonyl carbon, in (1) we observe angles of 128°, 117° and 155°. This is in contrast to the carbonyl carbon angles in (2) which are all ca 120° revealing a less strained system.
Functionalisation of the double bond joining the bridgehead in Taxol shows lower reactivity than expected. This may be attributed to the theory behind “hyperstable alkenes” which are alkenes who are less strained than their parent structure. Consequently there is a higher energy barrier to overcome the extra stability gained by the alkene being adjacent to the bridgehead sub-structure.[5]
Part(ii) Modelling Using Semi-empirical Molecular Orbital Theory
The limitations of MM have been exposed in that they do not account for electronic interaction and hence give limited information based merely on steric grounds as to why one conformation/isomer is favoured over another. Applying a quantum mechanical treatment and computation of wavefunctions can enable us to rationalise issues such as regioselectivity on electronic grounds.
2.1 Regioselective Addition of Dichlorocarbene

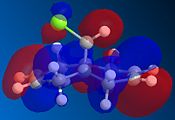
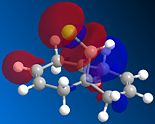
The reaction of the molecule (1) with electrophiles such as dichlorocarbene or peracids proves to be very regioselective. There is a choice of essentially geometrically identical double bonds in (1) to act as the nucleophilic HOMO in for example an electrophilic addition. We will attempt to compute an approximation to the valence-electron molecular wavefunction of molecule (1) by first minimising the geometry using the MM2 force field and then applying a MOPAC/PM6 calculation. 5 key molecular orbitals have been shown:
 |
 |
 |
 |
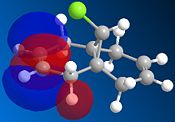 |
The key observation to make is that in (1) the LUMO+1 orbital (which corresponds to the C-Cl σ* bond) can be stabilised by good anti-periplanar overlap with the π cloud of the HOMO(-1) (corresponding to the anti/-exo wrt C-Cl) double bond). We suspect that as a result of this the C-Cl bond is weakened. Computing an IR spectrum of (1) and using (2) as a reference molecule in which no stabilising overlap is observed due to the absence the anti-double bond and orbitals of inappropriate symmetry will result in lower energy stretch C-Cl stretch.
To investigate this we will need to adopt a density functional approach. Following MM2 minimisation and MOPAC/PM6 minimisation both molecules were subject to B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation. We have also investigated the effects of an electron withdrawing (-CN) and donating group (-SiH3) on the anti-double bond. The results are summarised:
 |
 |
 |
 |
 |
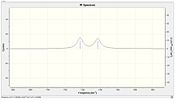 |
Similar spectra have been computed for the monoalkene 2 and the Silyl substituted 3 and Cyan substituted 4 dialkenes. The results are summarised in the following table:
|
Derivative |
C-Cl/cm-1 |
exo C=C/cm-1 |
endo C=C/cm-1 |
|
Dialkene |
770.92 |
1737.14 |
1757.37 |
|
Monoalkene |
774.95 |
n/a |
1758.05 |
|
SiH3 |
763.79 |
1690.26 |
1756.24 |
|
CN |
765.79 |
1706.27 |
1756.53 |
We observe a lower energy C-Cl stretch for the di-alkene of 770.9cm-1 compared to the monoalkene stretch of 775.0 cm-1. This is consistent with the fact that the bond is weakened with the π-σ* interaction from this exo C=C bond. The exo C=C bond is observed to be weaker than the endo C=C bond due to this interaction. There is little difference between the dialkene and monoalkene or -SiH3 and –CN substituted endo C=C bond stretching energies showing that this bond is not involved in any significant orbital interaction. Comparing the -SiH3 and –CN substitutions we see that for the silyl the C-Cl bond is ever so slightly weakened which is consistent with the fact that the group is electropositive/electrondonating and hence weakens the C-Cl bond further. This is in contrast to the electron withdrawing cyan group which strenghthens the C-Cl bond slightly by reducing the effect of the π-σ* interaction.
Part(iii) Structure based Mini project using DFT-based molecular orbital methods
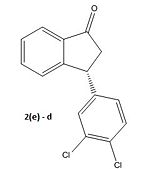
3.1 Enantioselective Formal Synthesis of (-)-Indatraline
Taylor and co-workers [6] have presented an asymmetric synthesis for the formal synthesis of the psychoactive compound (-)-Indatraline. The molecule of interest (2) is the optically active precursor (S)-3-(3,4-Dichlorophenyl)-2,3-dihydroinden-1-one; [R]20D -50.0 (c=1.1,CHCl3) Caution The scheme proposed in the paper is outlined below and an attempt has been made at the mechanism to fit this scheme.
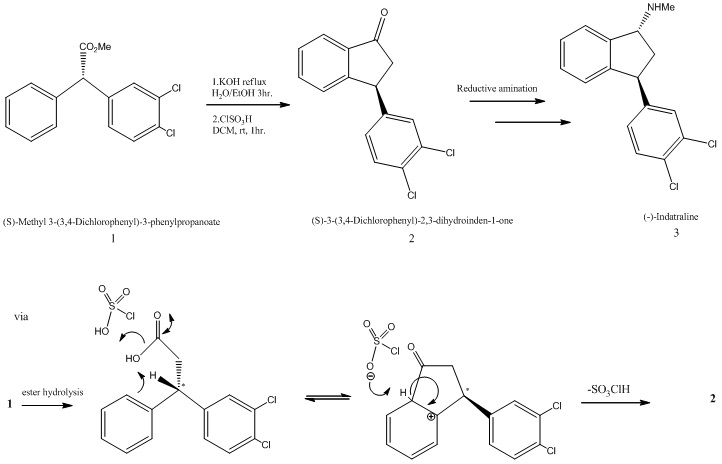
Molecule (1) a β,β-Diaryl-substituted,α, β-Unsaturated Esters was prepared using 3 mol %Cu(OAc)2 and 4 mol % of R JOSIPHOS, where ligand JOSIPHOS = (R)-1-[(S)-2-diphenylphosphino) ferrocenyl]ethyldicyclohexylphosphine). According to the paper, this was then hydrolysed and cyclised using HSO3Cl catalyst to give (2). A reductive amination then took place to supposedly give (-)-Indatraline. The stereochemistry of (2) does not logically seem to be as a consequence of the cyclisation step in which a 5 membered ring is fused onto a planar phenyl ring. Intuitively we would in fact expect the corresponding enantiomer of (2) which we call (2e) to be formed instead. Let’s take a look at the rearrangement required to form (2) in the cyclisation step:
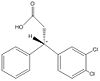 |
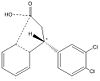 |
As it stands, from the above scheme to form (2) we would require inversion of the stereocentre which is not probable as this would require tunelling of the hydrogen. We therefore propose that (2) should in fact be the enantiomer (2)e in the paper.
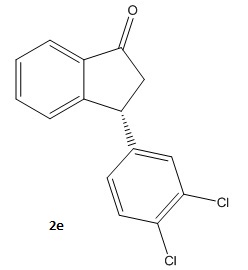
So going back to (2) we will attempt to compute the absolute optical rotation and show that it is in fact positive and contrary to the negative rotation in the paper. Firstly (2) is optimised using the MM2 force field. Optical rotation depends heavily on the conformer. We therefore seek the lowest energy conformer using the dihedral driver in ChemDrawBio3D to investigate the number of low energy conformers by rotating the dichlorinated phenyl ring with respect to the fused ring system. This is a good initial approximation using classical mechanics before we employ a more quantum mechanical treatment.
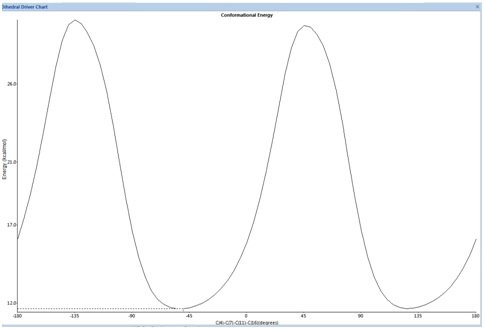
We obtain the following graph indicating two low energy conformational minima at -45° and 135°. The MOPAC/PM6 energy minimisation is then applied to refine the angles to -45.9° and 130.8°. Next we apply a Gaussian minimisation using the mpw1pw91 method and 6-31G(d,p) basis set. Both conformers are shown and defined as a and b below. We have also done the calculation for the enantiomer 2(e) to yield two more conformers which we define as c and d:
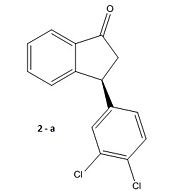 |
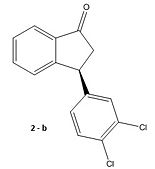 |
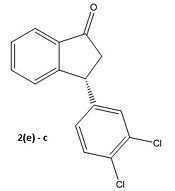 |
 |
We now compute the optical rotation using the Cambridge variation on the B3LYP density functional method with solvent chloroform and incident wavelength of light of 589nm (Sodium D line).
|
Conformer |
Free energy/ kJmol-1 |
Dipole moment/D |
[R]20D (CHCl3)/ ° |
|
a |
-4129910 |
4.219 |
-100 |
|
b |
-4129910 |
3.354 |
164 |
|
c |
-4129910 |
4.219 |
100 |
|
d |
-4129910 |
3.229 |
-15 |
Focusing firstly on (2), calculation yields identical sum of electronic and thermal free energies, effectively free energies, for both conformations of -1573.2a.u or -4129910kJ/mol. An identical computed total energy in the absence of solvent is quite plausible considering the only difference between the conformers is the positioning of the chlorine atoms which are far from any significant electron density on the molecule. To distinguish which of the conformers would be the most favorable we must consider the dipole moments. Conformer a has the larger dipole moment of 4.219D over b which has dipole moment 3.354D. As the solvent is non-polar chloroform, the conformer with the lowest dipole moment will be most favourable. We therefore conclude that conformer b is the most probable conformation.
By considering the sign only for conformer b we observe a contradiction with the computed value of [R]20D 164° (CHCl3) to the literature value of [R]20D -50°. Although the error in our calculation is likely to be large as we are considering an optical rotation of I50I See note the sign is inconsistent with the literature. This leads us to question the aforementioned unusual counter intuitive inversion of the stereocentre during the cyclisation inferred by the literature.
Inspection of the results for the enantiomers of conformers a and b, which we have labelled c and d respectively, shows the opposite sign of rotation as expected thus confirming the validity of our results. Experimentally we should expect conformer d to be the product and not b as shown in the literature.
However this accusation must be treated with caution. As mentioned, the error in the optical rotation calculation is likely to be large and further formal investigation of the transition state geometry would be necessary to verify the accusation See Module 3. However, from a purely mechanistic perspective, unless there is some quantum mechanical tunnelling leading to inversion at the stereocentre we would expect 2(e) to be the observed enantiomer with a probabale conformer d to be consistent with the negative optical rotation observed experimentally. To further improve on the reasoning behind choosing the conformer with the lowest dipole moment for the non-polar chloroform we could recompute the free energies, except this time with a the solvent factored into the calculation. We would then observe a difference in energy between the two conformers. This could then be used to weight the spectroscopic properties, in line with a Boltzman distribution, between the two conformers.
References
- ↑ Pierluigi Caramella*, Paolo Quadrelli, and Lucio Toma, An Unexpected Bispericyclic Transition Structure Leading to 4+2 and 2+4 Cycloadducts in the Endo Dimerization of Cyclopentadiene, 2002, 124, 1130-1131:*DOI:10.1021/ja016622h
- ↑ Stereochemistry of Electrocyclic Reactions R. B. Woodward, Roald Hoffmann J. Am. Chem. Soc.; 1965; 87(2); 395-397.*DOI:10.1021/ja0108a054
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838.*DOI:10.1021/jo00356a016
- ↑ J. Am. Chem. Soc., Vol. 103, No. 8, 1981 http://pubs.acs.org/doi/pdf/10.1021/ja00398a003 DOI:10.1021/ja00398a003
- ↑ J. Am. Chem. Soc., Vol. 103, No. 8, 1981 http://pubs.acs.org/doi/pdf/10.1021/ja00398a003
- ↑ J. Org. Chem. 2011, 76, 857–869 857 http://pubs.acs.org/doi/pdf/10.1021/jo102134v
