Transition States and Reactivity

Introduction

The aim of this lab was to investigate a number of Diels-Alder cyclic reactions using the program Gaussian, in order to determine the structure of the transition state formed during these reactions. The transition state in a reaction is the point of highest energy along a reaction coordinate, with a first derivative of zero, and a second negative derivative in the direction of the products, which occurs between the two energies of the reactants and the products, whose firsts derivative are also equal to zero. The enthalpy change of a reaction is determined by calculation of the difference in energy between these two points, and the activation energy corresponds to the difference in energy between the reactant minima and the transition state maxima.

In reality there are many degrees of freedom than seen in the 2D Reaction Coordinate plot, determined by the equation 3N-6, where N is the number of atoms in a molecule. The degrees of freedom can be used to plot a multidimensional Potential Energy Surface, and the reaction coordinate then plotted as a function of the degrees of freedom produced. Depending on the basis set selected, a greater number of basis vectors, such as with 631-G, can be utilised during calculation in order to produce a result with fewer approximations, at the expense of a longer calculation time. The Energy Profile normally corresponds to the minimum energy reaction pathway plotted from a Potential Energy Surface of a reaction, as there is the potential for there to be more than one saddle point on a Potential Energy Surface. In order to determine if the correct energy pathway is calculated using Gaussian, only one negative imaginary frequency should be seen, otherwise there is the possibility that the programme may have plotted another higher energy pathway instead.

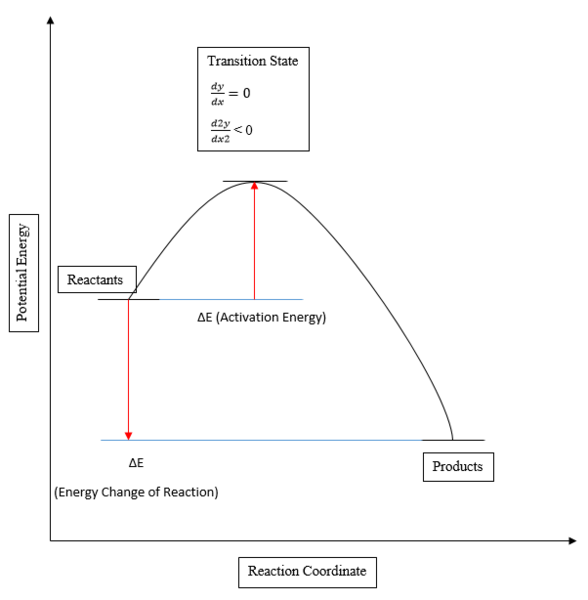
Figure 1 - Reaction Coordinate Diagram

Location of a transition state using Gaussian can be achieved via 3 different methods, depending on the initial knowledge of the transition state and the accuracy of the calculation required.

Nf710 (talk) 10:57, 16 April 2018 (BST) Some degree of confusion here. You can get this info about the second derivative by diagonalizing the hessian matrix and this gives you the normal modes(eigen vectors) the force constants (eigenvalues).

Method 1

Involves the initial optimisation of the reactants and then placement of the reactants in a geometry similar to that of the transition state (such as 2.2Å being the average between the combined van der Waals radii and a C-C bond length), hence this method is unreliable unless some knowledge of the transition state is known. Although this is the quickest of the methods suggested, it is also the most unreliable, potentially producing multiple transition states, imaginary negative values or fail altogether. This method is best left for smaller systems if completely necessary.

Method 2

Requires initial optimisation of the reactants, but during calculation of the transition state, bonds included in the reaction are frozen in place. This allows the system to be as close to the transition state as possible before optimisation, by allowing the unfrozen parts of the system to minimise around the frozen ‘bonds’. This method is more reliable than the previous method and almost as fast, yet still requires some understanding of the transition state before application.

Method 3

Requires little knowledge of the transition state, and allows determination of the transition state from either the reactants or the products after optimisation. Using the desired product, the bonds which are formed during the transition state are frozen and placed a sensible distance apart (such as 2.4Å for a S-C bond). The broken bonds are frozen and optimised, then the transition state calculated. Although this is the most reliable of the methods, this method may fail if the transition state closely resembles the structure of the reactants when optimising and changing the structure from the products, as well as requiring multiple additional steps.

All these methods use a combination of both the semi-empirical method PM6 and the DFT method B3LYP, the former of which is quicker and used to optimise the structures initially, before the latter can further optimise the structure produced, giving a more reliable structure via the use of a greater amount of basis vectors.

Exercise 1

(Fv611 (talk) Good job overall.)

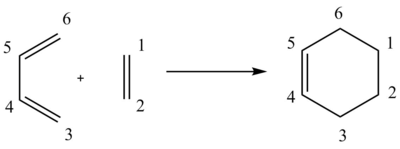
The electrocyclic reaction between Ethene and Butadiene to form Cyclohexene was investigated to determine the orbitals involved in the formation of the transition state of the reaction, the energies of the relevant orbitals and the change in the bond lengths between the carbons upon formation of the transition state and products. The carbons are labelled as shown in Figure 2 and the change in bond lengths between the carbons reported in the table below.

Reaction Scheme

Figure 2 - Reaction Scheme for the reaction of ethene and butadiene

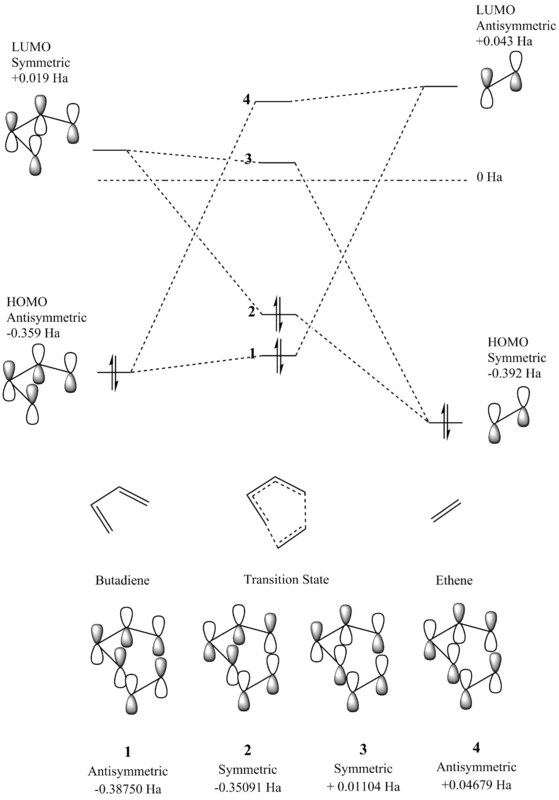
Molecular Orbital Diagram

Figure 3 - Molecular Orbital Diagram for the reaction of ethene and butadiene

In order for the orbitals to overlap and combine, the orbitals must have the same symmetry to produce a molecular orbital of that same symmetry. Therefore, only symmetric-symmetric and antisymmetric-antisymmetric interactions can occur to produce a non-zero orbital overlap integral and are ‘allowed’, conversely a symmetric-antisymmetric orbital overlap would produce a zero value orbital overlap integral and as such is a ‘forbidden’ reaction. The final produced molecular orbitals are of the same symmetry as the original molecular orbitals, and the energy of the products normally lower than that of the reactants, as discussed earlier. However, as this diagram depicts the formation of the transition state, the molecular orbitals are higher in energy than the final orbitals formed, as shown by the reaction coordinate diagram.

HOMOs and LUMOs for Reactants and Transition States

Ethene HOMO

Ethene LUMO

Butadiene HOMO

Butadiene LUMO

1 - Transition State HOMO -1

2 - Transition State HOMO

3 - Transition State LUMO

4 - Transition State LUMO +1

Bond	Reactants Bond Length/Å	Transition State Bond Length/Å	Product Bond Length/Å
C1-C2	1.35520	1.38177	1.53773
C2-C3	-	2.11468	1.53582
C3-C4	1.33345	1.37979	1.49266
C4-C5	1.47077	1.41109	1.33305
C5-C6	1.33345	1.37979	1.49266
C6-C1	-	2.11468	1.53582

Table 1 - Carbon Bond Lengths in the Formation of Cyclohexene

(Fv611 (talk) You should have explicitly stated that your carbon numbering is the one you use in your reaction scheme.)

From the table above, it can be seen that upon formation of the transition state, bonds C1-C2, C3-C4 and C5-C6 all lengthen as the sp hydridisation increases. Conversely, C4-C5 decreases from 1.47Å to 1.41Å due to the formation of a double bond from the single bond seen in the reactants and the increased s character of the MO. This bond further decreases upon completion of the double bond formation. The initial C6-C1 and C2-C3 'bonds' shorten in length, producing a value of 1.53582Å, incredibly close to the 1.54Å for a sp³-sp³ C-C bond¹, showing the structure was successfully optimised by Gaussian. Due to the increased s character of the bonds when closer to the sp² carbons and C=C bond, there is a slight decrease in bond length from C1-C2 to C2-C3/C6-C1. As expected this increase in s character continues when looking at the bonds around the sp² C5 and C4, with the C3-C4/C5-C6 having intermediate values between the 1.54Å for a C-C bond and 1.34Å for an alkene C=C bond. This is consistent with the reported sp³-sp² value of 1.50Å¹. The initial transition state produces a bond length of 2.11468Å for C2-C3/C6-C1, which decreases to 1.53582Å upon formation of cyclohexene. The initial bond length of 2.11468Å is comparable to the sum of two carbon van der Waals radii (3.400Å)², and shows a bonding character interaction due to the shorter length observed.

Transition State Vibration and IRC

Figure 4 - Reaction Path at the Transition State Vibration

Figure 4 shows the vibration corresponding to the imaginary frequency produced by the transition state, which represents the reaction path at the transition state. In the IRC, the bonds from the diene and alkene form at the same time, and such is a synchronous, concerted reaction.

Transition State IRC

Exercise 2

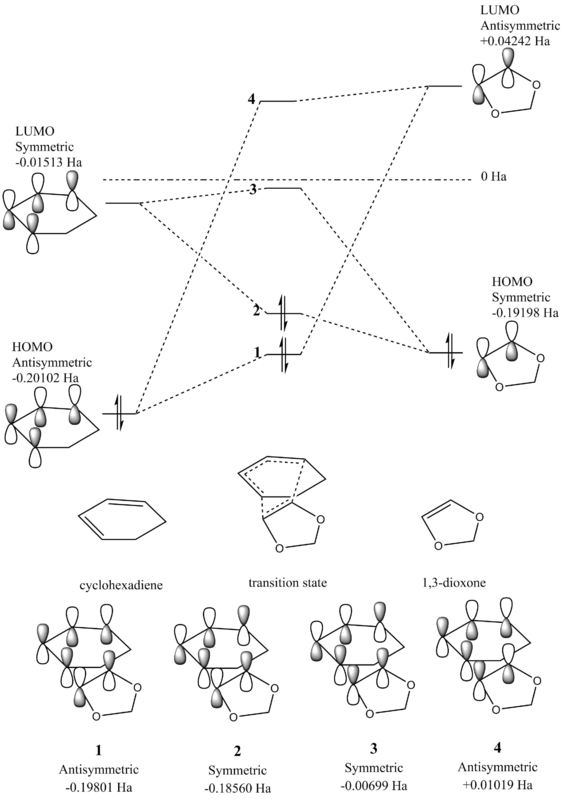
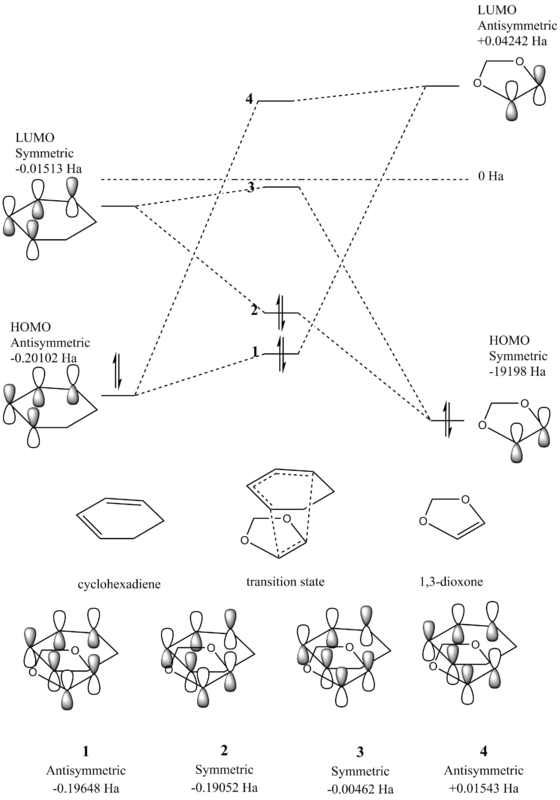
The molecular orbital diagrams for the Diels-Alder reaction between 1,3-dioxone and cyclohexadiene were produced to determine the molecular orbitals involved and the overlap of the orbitals in the transition state. Here the production of both the endothermic and exothermic products was investigated, where the approach of the dienophile 1,3-dioxone differs. During formation of the endothermic product, the ring oxygens approach beneath the alkene bonds in cyclohexadiene due to a favourable stabilising interaction. However for the exothermic product, the ring oxygens are positioned away from the alkene bonds. As seen in the previous exercise, only overlap between orbitals of the same symmetry is allowed for a reaction to occur.

Reaction Scheme

Figure 4 - Reaction Scheme for the Reaction of Cyclohexadiene and 1,3-dioxole

Molecular Orbital Diagram

Exothermic MO Diagram	Endothermic MO Diagram

Figure 5 - Molecular Orbital Diagram for the Reaction of Cyclohexadiene and 1,3-dioxole

A standard Diels-Alder reaction involves the combindation of a diene and a dienophile, where the HOMO of the diene interacts with the LUMO of the diene. However in the reaction investigated here, the electron donating oxygens in the 1,3-dioxone ring increase the energy of the HOMO of the alkene, and thus instead the HOMO of the alkene interacts with the LUMO of the diene in an inverse demand Diels-Alder reaction. Here it can be seen that molecular orbitals 1, 3 and 4 for the endothermic product are higher in energy than the exothermic counterparts, whilst molecular orbital 2 is lower in energy in the endothermic transition state than the exothermic. This effect seen in the endothermic product is due to secondary orbital interactions and is discussed later on, shown in the molecular orbital Jmol images below.

(Fv611 (talk) The endo and exo prefixes are absolutely not related to the thermodynamics of your reaction. This is something you should know in your third year. Additionally you have not dranw the correct endo diagram: you state the numerical values of your MO relative energies, so why wouldn't you order them correctly?)

HOMOs and LUMOs for Reactants and Transition States

1,3-Dioxole HOMO

1,3-Dioxole LUMO

Cyclohexadiene HOMO

Cyclohexadiene LUMO

1 - Exo Transition State LUMO +1

2 - Exo Transition State LUMO

3 - Exo Transition State HOMO

4 - Exo Transition State HOMO -1

1 - Endo Transition State LUMO +1

2 - Endo Transition State LUMO

3 - Endo Transition State HOMO

4 - Endo Transition State HOMO -1

Reaction Energies

Type of Reaction	Energy of Reactants/kJ mol^-1	Energy of Transition State/kJ mol^-1	Energy of Product/kJ mol^-1	Activation Energy/kJ mol^-1	Reaction Energy/kJ mol^-1
Endo	-1313771.847	-1313622.1573	-1313852.8626	149.6897	-81.01537
Exo	-1313771.847	-1313614.3096	-1313845.7396	157.53763	-73.8926

Table 2 - Activation and Reaction Energies for the Reactions between Cyclohexadiene and 1,3-dioxole

From the calculated data in the table above, the exothermic product is shown to have a greater activation energy than the endothermic product. This can be explained by the lack of a non-bonding stabilising interaction between the ring oxygen orbitals overlapping with the alkene bond orbitals during the transition state, meaning the energy of the exothermic transition state is higher than that of the endothermic pathway. This secondary orbital overlap can been seen below (Figure 6). Both reactions are exothermic and thermodynamically favourable enough to overcome the decrease in entropy upon formation of the product. However, the endothermic product is the lower in energy and therefore most stable of the products, which may be due to reduced steric interactions with 1,3-dioxole species avoiding steric clashes with the carbon chain bridging the 2 C=C bonds. This leads to a further favouring of the endothermic product, with both the stabilising oxygen non-bonding interactions and the lack of steric repulsion by bridging carbons, as seen in the data produced. (It should be noted that upon optimisation of the cyclohexadiene, a negative frequency was observed, corresponding to the stretching of the sp³ C-H bonds. This resulted in a slightly higher energy in the products than expected.)

Exo Transition State HOMO

Endo Transition State HOMO

Figure 6 - Secondary Orbital Effect

Nf710 (talk) 11:08, 16 April 2018 (BST) Nice section. You jmols are very nice. you have got slightly incorrrect answers for you reaction energies so I suspect on of your product may not have been optimized properly. However yo have come to the correct conclusions.

Exercise 3

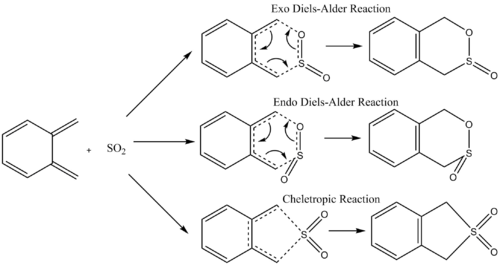
O-Xylylene and sulfur dioxide undergo multiple cycloaddition reactions, which consist of a Diels-Alder and Cheletropic reaction, forming 10 and 9 membered rings respectively with the external cis-butadiene and 6 membered with the internal. During the [4+2] Diels-Alder reactions, the orientation of the SO₂ to the external cis-butadiene during formation of the transition state allows production of an exothermic and endothermic product. The preference of forming either the exothermic or endothermic product via a Diels-Alder reaction, or the cheletropic product, was investigated here by optimisation of each transition state at the PM6 level, and the energies calculated from the data. These pathways were then compared to the [4+2] cycloaddition pathways possible with the internal cis-butadiene.

(You should still count members of a ring by the smallest continuous joined system ie 5 and 6 for both external and internal reaction products Tam10 (talk) 12:03, 4 April 2018 (BST))

Reaction Scheme

Figure 7 - Reaction Scheme for the Reaction of o-Xylylene and Sulfur Dioxide

External Transition State IRCs

Diels-Alder Exo Transition State IRC	Diels-Alder Endo Transition State IRC	Chemetropic Transition State IRC

(Your exo TS is actually endo as well Tam10 (talk) 12:03, 4 April 2018 (BST))

External Reaction Energies

Type of Reaction	Energy of Reactants/kJ mol^-1	Energy of Transition State/kJ mol^-1	Energy of Product/kJ mol^-1	Activation Energy/kJ mol^-1	Reaction Energy/kJ mol^-1
Diels-Alder Endo	156.39	235.4534	56.4044	79.0634	-99.9856
Diels-Alder Exo	156.39	235.4612	55.7804	79.0712	-100.6096
Cheletropic	156.39	257.5612	0.013	101.1712	-156.377

Table 3 - Activation and Reaction Energies for the External Reactions between o-Xylylene and Sulfur Dioxide

From Table 3, it can be seen that the Diels-Alder reactions form a more favourable transition state than the Cheletropic pathway, although the Cheletropic product is lower in energy, at an almost 0 value, corresponding to the thermodynamic product. The increased stability in the product is due to the formation of 2 C-S bonds, and lack of breaking of a S-O bond. Although the C-O bond energy formed during the Diels-Alder reaction is greater than the C-S bonds only formed during the Cheletropic reaction, 358kJ/mol compared to 272kJ/mol³, this does not compensate the energy used breaking the S-O bond. The activation energy for the Cheletropic reaction is high due to the formation of a strained 5 membered ring, as opposed to the 6 membered ring formed during the Diels-Alder reaction. All products lead to a decrease in energy due to the produced aromatic molecule, with the Diels-Alder Endo product being the kinetic product due to the smallest activation energy, albeit only by a marginally small amount than the exothermic. The ability for o-Xylylene to form planar aromatic products is the reason for its high reactivity and low stability, at least at the external cis-butadiene site.

Reaction Coordinate Diagram

Figure 8 - Reaction Coordinate Diagram for the Reaction of o-Xylylene and Sulfur Dioxide

Internal Transition State IRCs

Exo IRC	Endo IRC

Internal Reaction Energies

Type of Reaction	Energy of Reactants/kJ mol^-1	Energy of Transition State/kJ mol^-1	Energy of Product/kJ mol^-1	Activation Energy/kJ mol^-1	Reaction Energy/kJ mol^-1
Diels-Alder Endo	156.39	265.382	170.5834	108.992	14.1934
Diels-Alder Exo	156.39	273.1404	174.9956	116.7504	18.6056

Table 4 - Activation and Reaction Energies for the Internal Reactions between o-Xylylene and Sulfur Dioxide

When reacting with the internal cis-butadiene, there is no overall aromatic stabilisation, and the alkene bonds are left as unsubstituted and terminal. Hence in comparison to the external reaction, the internal is far less favoured, as not only is the activation energy higher, but the disturbing of the conjugated pi system leads to a destabilisation of the products in comparison to the reactants. From Table 3, it can be seen that the activation energy upon formation of the transition state with the internal cis-butadiene bond is greater than with the external, with both the endothermic and exothermic transition states. The overall reaction energy is actually positive for this cycloaddition, due to an increase in energy in the products from the reactants. Upon reacting at the internal cis-butadiene, not only is there a lack of aromatic stabilisation in comparison to the external reaction, but the planar conjugated structure is also disturbed.

Conclusion

The reactants, transition states and products were all successfully optimised using Gaussian, with imaginary frequencies only obtained when expected on a transition state. Study into multiple electrocyclic reactions allowed determination of the molecular orbitals involved in the production of the transition state, of the change in bond lengths during a reaction, of the kinetic and thermodynamic products and how effects from non-bonding orbital interactions and aromatic stabilisation may affect the products produced. Use of both 631-G and PM6 allowed practice of situations with different basis sets and methods to produce the desired optimised transition state and products required for energy calculations and discussion, which agreed with the expected trends.

References

1. Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9.

2. S. S. Batsanov, Inorg. Mater., 2001, 37, 871-885.

3. Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds", 1958, 2nd ed., Butterworths, London