Rep:Mod:npa11 1C
Computational Lab 1C-Part One
Computational software including Avogadro, Avogadro 2.0, Gaussian, Conquest and Mercury have been tasked with calculating a series of interesting problems with the end aim of comparing the results collected with literature. Part one investigates Kinetic and thermodynamic control for the formation and hydrogenation of the cyclopentadiene dimer followed by confgormational analysis and spectral generation of intermediates of Taxol. Part two works alongside the wet chemistry preformed in the lab and aims to help analayse and determine the products that have been created by asymmetric catalytic epoxidation of an alkene via the Jacobsen and Shi catalysts. The analysis aims to provide insight into the transition state and the selectivity of both catalysts.
Hydrogenation of Cyclopentadiene Dimer
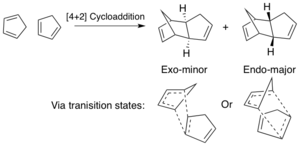
The cyclisation of cyclopentadiene gives rise to two conformations an endo and an exo form, as shown in scheme 1. This is a famous [π4s+π2s] thermal Diels-Alder reaction that occurs via a Huckel topology transition state. A MMFF94s method has been employed to optimise the structures with a conjugate gradient algorithm to allow determination of the energies of the specific structures and thus which conformer is thermodynamically most stable.
|
Energy (Kcal/mol) | |||
|---|---|---|---|---|
| Total electrostatic | 13.01371 | |||
| Total Van der Waal's | 12.80130 | |||
| Total out of plane bending | 0.01495 | |||
| Total torsional | -2.73078 | |||
| Total stretch bending | -2.04136 | |||
| Total Angle stretch Bending | 30.77282 | |||
| Total Bond stretching | 3.54284 | |||
| Total Energy | 55.37346 |
|
Energy (Kcal/mol) | |||
|---|---|---|---|---|
| Total electrostatic | 14.18456 | |||
| Total Van der Waal's | 12.35626 | |||
| Total out of plane bending | 0.02210 | |||
| Total torsional | -2.94978 | |||
| Total stretch bending | -2.08211 | |||
| Total Angle stretch Bending | 33.19275 | |||
| Total Bond stretching | 3.46694 | |||
| Total Energy | 58.19073 |
As determined from the total energy of the two possible dimers, it has been shown that the most stable dimer is in fact the Exo dimer. This has a lower total energy by 11.8 KJ/mol which results in this product being the most thermodynamically favourable. This then indicates that the reaction proceeds under kinetic control as it is known that the reaction proceeds selectively to give the endo conformation. This is a direct result form the extra electronic stabilization energy gained in the transition state by secondary orbital overlap when the incoming dieneaphile is endo, which lowers the energy of the transition state, thus causing the endo product to be the fastest formed, the kinetic product. The endo product has a lower Van der Waal's energy than that of the exo product due to the reduced distance of the overhanging methylene bridging protons and the two protons of the cyclopentene ring. Torsional and stretch bending energies are also lower than that of the exo product. The Torsional strain is reduced in the endo product due to antiperplanar-gauche arrangement of the alkyl substituents causing an increase in hyperconjugation and reduced steric clash that would occur in the gauche-gauche conformation, the exo product. The bending energy is greatest in the endo product due to the largest distortion from the ideal sp3 bond angle of 109° to 100.2°, whilst in the exo the angle is compressed to 102.7°.Finally the electrostatic energy shows that there is a small amount of destabilisation in the endo product, which can be accounted by the fact the alkenes in the product are closer together leading to pi-pi repulsions. All other energies are higher in the endo form. All of the above agrees with literature of computational experiments and experimental observations. [1],[2]
The hydrogenation of the Endo-dimer also results in two further possible outcomes depending on which double bond is hydrogenated. The two possible dihydro derivatives are shown in reaction scheme two and are labeled A and B. Again analysis of the relative stabilities of both forms has been preformed to identify whether the reaction is under kinetic or thermodynamic control.
Pentahelicene |
Derivative A
Pentahelicene |
Derivative B
| Product from hydrogenation | Energies (Kcal/mol) | |||||||
|---|---|---|---|---|---|---|---|---|
| Total Energy | Total Electrostatic Energy | Van der waals Energy | Total out of plane bending | Total torsional | Total stretch bending | Total angle bending | Total Bond stretching | |
| Derivative A | 50.72287 | 5.12102 | 13.28407 | 0.01536 | 0.04272 | -1.92696 | 30.87797 | 3.30869 |
| Derivative B | 41.25749 | 5.14702 | 10.63678 | 0.00028 | -0.37805 | -1.65717 | 24.68556 | 2.82306 |
| Prolonged hydrogen product | 38.01467 | 0.00000 | 10.89720 | 0.00000 | 3.30168 | -1.51556 | 22.64378 | 2.68757 |
The dihydro derivative B is the thermodynamic product as indicated by the lower total energy value. It is known from literature that the major derivative formed is B. This therefore means that the reaction is under thermodynamic control.[3] Derivative A has a higher energy and is therefore less stable than B, a factor causing this results from the double bond being located in the norbornene ring, which means the Bending angle energy is higher due to larger ring strain. In terms of Van Der waals it can also be noted that derivative B allows more attractive contacts than A as more H-H shorts contacts are closer to the maximum attractive distance on the Lenard-Jones potential(~240pm) for B whilst A has interactions that lie further away from this region. Consequently the Van Der Waals energy for B is lower and thus the derivative is stabilised for this energy factor. The torsional energy for A is higher than that of B due to an eclipsing of the allyl group, there is a syn-periplanar arrangement of the allylic hydrogens. Comparatively the allylic hydrogens are staggered in derivative B, this reduces steric clashing and allows a secondary orbital overlap to form, sigma-conjugation, resulting in a lower bond stretch, angle bending and out of plane bending energy. Finally the electrostatic energy of A is less than that of B due to the distance between the delta-negative allylic carbons and the delta-positive overhanging hydrogens is reduced, thus allowing for an increased interaction in derivative A. As seen between both the hydrogentated and monohydrogenated product the main destabilising interaction is the angle strain due to the restriction of being locked in rings constricting the bond angles of the would be planar 120 degrees of the alkene to around 110 degrees.
The prolonged hydrogenation product has no electrostatic interaction energy due to the removal of the alkenes, which removes the large electron pi-systems. This accounts for the lower total energy of the system. However due to increased geometry strain the torsional, Van Der Waals and angle bending energies have increased which have resulted in the energy not lowering by a larger amount resulting in why prolonged conditions may be needed to cause complete total hydrogenation.
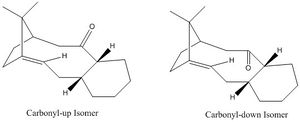
An intermediate in the synthesis of Taxol after the oxy-cope rearrangement has two possible isomers, which are in equilibrium are shown below in scheme 3 and they are the carbonyl up and down isomers.[4] Furthermore for each isomer there are four possible conformations, which are related by a series of rotations around bonds.
| Isomer | Structure | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conformation one (Chair) | Conformation two (Chair 2) | Conformation three (Twistboat) | Conformation four (Twistboat 2) | |||||||||||||
| Carbonyl-up |
|
|
|
| ||||||||||||
| Carbonyl-down |
|
|
|
| ||||||||||||
| Isomer | Energies (Kcal/mol) | |||
|---|---|---|---|---|
| Conformation one (Chair) | Conformation two (Chair 2) | Conformation three (Twistboat) | Conformation four (Twistboat 2) | |
| Carbonyl-up | Total energy=82.77345, Electrostatic energy=0.19632, Van Der Waal's energy=35.43746, Out of plane bending energy=1.60638, Torsional energy=3.24791, Stretch Bending energy=0.08114, Angle Bending energy=33.7149, Bond stretching energy=8.48915 | Total energy=70.54436, Electrostatic energy=0.30282, Van Der Waal's energy=33.16957, Out of plane bending energy=0.96832, Torsional energy=0.16130, Stretch Bending energy=-0.06028, Angle Bending energy=28.31389, Bond stretching energy=7.68874 | Total energy=78.014202, Electrostatic energy=0.31436, Van Der Waal's energy=33.47799, Out of plane bending energy=0.99021, Torsional energy=3.88139, Stretch Bending energy=0.05009, Angle Bending energy=31.17642, Bond stretching energy=8.12327 | Total energy=88.48857,Electrostatic energy=0.16583, Van Der Waal's energy=36.72116, Out of plane bending energy=1.91947, Torsional energy=6.99724, Stretch Bending energy=0.14106, Angle Bending energy=34.14311, Bond stretching energy=8.40069 |
| Carbonyl-down | Total energy=60.55284, Electrostatic energy=-0.05173, Van Der Waal's energy=33.23162, Out of plane bending energy=0.85013, Torsional energy=0.25311, Stretch Bending energy=-0.14445, Angle Bending energy=18.8175, Bond stretching energy=7.59631 | Total energy=75.23415, Electrostatic energy=0.40700, Van Der Waal's energy=35.62887, Out of plane bending energy=1.51034, Torsional energy=7.98303, Stretch Bending energy=-0.20151, Angle Bending energy=21.47263, Bond stretching energy=8.43380 | Total energy=66.32416, Electrostatic energy= -0.04493, Van Der Waal's energy=35.08321, Out of plane bending energy=0.84539, Torsional energy=3.17650, Stretch Bending energy=-0.06107, Angle Bending energy=19.57785, Bond stretching energy=7.74722 | Total energy=73.63756, Electrostatic energy=0.82753, Van Der Waal's energy=35.25310, Out of plane bending energy=0.68756, Torsional energy=1.67139, Stretch Bending energy=-0.21185, Angle Bending energy=27.72066, Bond stretching energy= 7.68917 |
Atropisomers are stereoisomers that result from hindered rotation about single bonds due to a high steric strain energy barrier to rotation, which allows the separation of conformers. [5] The above Taxol intermediates are a perfect example of this type of isomerism. From the results it can be seen that the lowest energy conformation lies in the intermediate with the carbonyl down and the cyclohexane ring in a chair conformation, its total energy is 60.6 Kcal/mol. The reaction proceeds under thermodynamic control as was suggested by paqutte, that the reaction can proceed under equilibrating conditions, resulting in the carbonyl down derivative dominating. The energy of the conformation is controlled by the cyclohexane arrangement due to larger rings being more flexible at adapting their geometry, thus each derivative has four energy minima, Two chair and two twist boat conformations. The twist chair conformations were attempted, however as this is a global maximum between the two minima Avogadro forced the conformation back to a chair or twistboat conformation. Similarly this occurred with the boat structure as this is also a maximum due to eclipsing of two bonds and suffers steric clashes of hydrogen atoms that lie within the repulsive region of the Van Der waals distance. Additionally any planar structures that may be suggested have been ignored as the angular strain would be too great and all bonds would be eclipsed leading to a very high energy conformation.[6] For both it can be seen that the most stable conformation is when there is a chair configuration of the cyclohexane ring, which is due to the fact that this allows more gauche interactions than the twist boat conformations, giving larger stabilisation energies via hyperconjugation. The difference between the two chair conformations for both carbonyl up and down isomers is due to the fact that in one chair conformation the carbonyl will be axial, whilst in the other it will be equatorial. This causes the system to suffer less repulsion when the carbonyl is equatorial, as noted in the reduced Van Der Waal's energy between both pairs of conformers. An interesting observation is that for both systems that one of the twistboats is lower in energy than that of one of the chair conformations, this in part can be accounted by the reduction in angle bending, torsion and electrostatic energy.
Hyperstability
|
Energy (Kcal/mol) | |||
|---|---|---|---|---|
| Total electrostatic | 0.00000 | |||
| Total Van der Waal's | 31.50001 | |||
| Total out of plane bending | 0.07584 | |||
| Total torsional | 8.14314 | |||
| Total stretch bending | 0.43897 | |||
| Total Angle stretch Bending | 24.71858 | |||
| Total Bond stretching | 6.67300 | |||
| Total Energy | 71.54954 |
The Alkene in this product reacts surprisingly slow due to Bredt's rule, which states that double bonds cannot be placed at the bridgehead of a bridge ring system, unless the ring is large enough. This arises because the torsional strain, bond and angle strain become so large they destabilise the molecule. The system does have a large enough ring i.e. a ring larger than nine carbons, which allows reduced strain in the system. However when addition to the alkene occurs the tertiary carbocation can't form a planar structure and thus doesn't benefit as efficiently from hyperconjugation as it should do if it had been allowed to adopt a planar geometry with bond angles of 120 degrees and sp2 orbitals. As a direct consequence this means that the energy of the transition state is higher than expected and it therefore slows down the rate of addition to the alkene due to the increased activation barrier. [7] Additionally the most stable hydrogenated product has been generated and its energy has been calculated using the same methods. From the data it is observed that the stability of the hydrogenated product is less than that of unhydrogenated derivatives. This is hyperstability of the alkene and arises due to increased angle strain when the alkene is hydrogenated or when the alkene undergoes any reaction that causes the hybridisation to alter from sp2 to sp3.[8]
Spectroscopic Simulation Using Quantum Mechanics
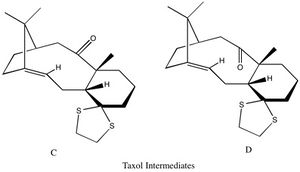
The ability to simulate spectroscopic data via computational means is being tested and compared to literature values for another derivative of taxol. Two possible derivatives that proceed on from the intermediates shown previously are depicted below and labelled C and D respectively. These form after the previous intermediates have been refluxed in tetrahydrafuran for several days.
Energy analysis has been preformed to determine which is this most stable. A MMFF94s force field has been employed to calculate the energy breakdown and the total energy of intermediates C and D.
| Intermediates Of Taxol | Energies (Kcal/mol) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Energy | Total Electrostatic Energy | Van der waals Energy | Total out of plane bending | Total torsional | Total stretch bending | Total angle bending | Total Bond stretching | ||||
Derivative C
|
104.76669 | -7.26207 | 52.06891 | 1.27568 | 11.13519 | 0.24916 | 31.40697 | 15.89285 | |||
Derivative D
|
100.45078 | -6.06522 | 49.27496 | 0.91893 | 9.70312 | 0.61611 | 30.96545 | 15.03743 | |||
From the energy data provided above it can be seen that the most thermodynamically stable conformation is derivative D, which is a carbonyl-down isomer and is more stable due to lower energies in all categories. This conformer has therefore been taken on to preform quantum mechanical calculations to generate a predicted NMR spectrum. The most stable isomer should give the best agreement with the experimentally calculated NMR by L. Paquette et. al. In this conformation the five memebered ring adopts an envelope structure as this is the lowest energy configuration for the five memebered ring. However as for the taxol intermediates seen above the main factor determining its energy is the conformation of the 6 memebered ring, with the lowest energy provided by the chair conformation.
 |
Computational Result (ppm) DOI:10042/26536 | Experimental Results (ppm) [9] |
|---|---|---|
| 0.63 (1H) | 1.03 (3H, s) | |
| 0.96 (3H) | 1.03 (3H, s) | |
| 1.22 (2H) | 1.07 (3H, s) | |
| 1.30 (1H) | 1.10 (3H, s) | |
| 1.37 (1H) | 1.10 (3H, s) | |
| 1.52 (2H) | 1.20 to 1.50 (3H, m) | |
| 1.59 (1H) | 1.20 to 1.50 (3H, m) | |
| 1.66 (1H) | 1.20 to 1.50 (3H, m) | |
| 1.85 (2H) | 1.70 to 2.35 (6H, m) and 1.58 (1H, t) | |
| 2.00 (2H) | 1.70 to 2.35 (6H, m) and 1.58 (1H, t) | |
| 2.28 (1H) | 1.70 to 2.35 (6H, m) and 1.58 (1H, t) | |
| 2.34 (2H) | 1.70 to 2.35 (6H, m) and 1.58 (1H, t) | |
| 2.48 (1H) | 2.35 to 2.70 (4H, m) | |
| 2.56 (1H) | 2.35 to 2.70 (4H, m) | |
| 2.61 (1H) | 2.35 to 2.70 (4H, m) | |
| 2.81 (2H) | 3.00 to 2.70 (6H, m) | |
| 2.93 (2H) | 3.00 to 2.70 (6H, m) | |
| 3.00 (1H) | 3.00 to 2.70 (6H, m) | |
| 3.14 (2H) | 3.00 to 2.70 (6H, m) | |
| 6.00 (1H) | 5.21 (1H,s) |
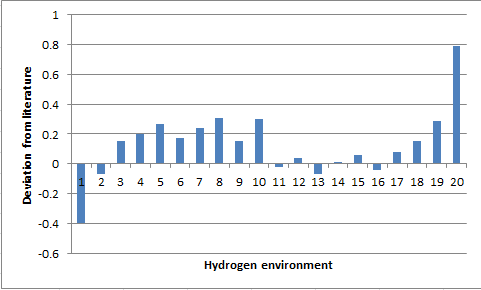
The data generated from quantum calculations provides results that are in fairly good agreement with literature. Both spectra yield the allylic proton to be in the most deshielded environment and the computed spectra manages to distinguish the anisotropic protons of a CH2 group with the proton opposite the alkene being most deshileded due to ring currents that the pi-system generates. Again the simulated spectra predicts correctly that the protons opposite the carbonyl group are anisotropic due to ring currents causing one environment do be downfield with respect to the other. The limitation with the simulated NMR is that the computation is run with the molecule being stationary, this leads to some environments being anisotropic. However in real systems rotations occur about bonds causing environments to coincide. This is seen in the methyl groups that have been split and show unity integration values where as in literature all protons are in an identical environment in the methyl group. A possible but long winded solution to this would be to generate many structural variations and calculate the NMR for each and average the result simulating real molecules and fluxionality. Additionally had there been no time restrictions J-couplings could have been determined and would give greater use for simulated NMR. The deviation from literature is small, with the most significant deviation corresponding to the most deshielded environment in the molecule. This is the alkene proton and deviates by +0.79ppm, a likely cause to this deviation is the sensitivity of computational NMR to the adopted conformation, with the real life situation adopting a variation of the structure.
 |
Computational Result (ppm)DOI:10042/26536 | Experimental Results (ppm) [9] |
|---|---|---|
| 22.60 (1C) | 19.83 | |
| 24.17 (1C) | 21.39 | |
| 24.60(1C) | 22.21 | |
| 26.52(1C) | 25.56 | |
| 28.42 (1C) | 30.00 | |
| 32.58 (1C) | 30.84 | |
| 33.73 (1C) | 35.47 | |
| 38.73 (1C) | 36.78 | |
| 41.20 (1C) | 38.73 | |
| 44.14 (1C) | 40.82 | |
| 45.80 (1C) | 43.28 | |
| 48.12 (1C) | 45.53 | |
| 49.67 (1C) | 50.94 | |
| 55.05 (1C) | 51.30 | |
| 65.93 (1C) | 60.53 | |
| 93.26 (1C) | 74.61 | |
| 120.23 (1C) | 120.90 | |
| 148.00 (1C) | 148.72 | |
| 213.04 (1C) | 211.49 |
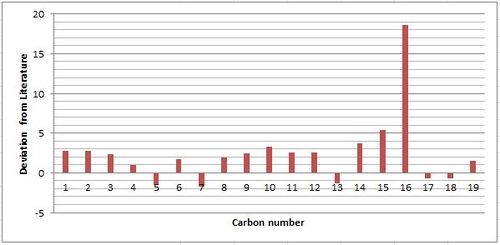
The carbon 13 NMR predicted is in good agreement with literature with the largest deviation occurring at 93.26 ppm for the simulated NMR. This deviation can be accounted for by the presence of the two adjacent sulfur atoms, which the DFT basis set employed fails to note the effect of the more prominent spin-orbit coupling occurring from the heavier element. This effect is also observed for the other two carbons that are adjacent to one sulfur atom, however the deviation is less pronounced. Calculations could be preformed to determine the effect of the sulphur by measuring the deviation from known examples and applying the resulting correction factor. The plotted graph shows that the general deviation from literature is positive, which can be explained by the movement away from using an actual source of TMS when experimental NMR is preformed. Most NMR spectrometers are now capable of holding the frequency of the TMS standard removing the need for it to be present in the sample or even as an external reference. This leads to a potential source of error associated with experimentally preformed NMR and leads to the deviations other than the ones previously mentioned to be insignificant.
As a result from both generated NMR spectrums using a very simple DFT basis set and understanding that the approximations used to solve the schrodinger equation may lead to deviations, computational results can generate a useful spectrum that can help assign experimental NMR spectrums and thus help confirm the identity of the product in question.
Energy Calculations
The free energy of Both Taxol intermediates above have been calculated and are presented in the subsequent table.
| Intermediate | Sum of Electronic and Thermal Free energy (Hartree) DOI:10042/26609 , DOI:10042/26536 |
|---|---|
| Derivative C | -1651.451 |
| Derivative D | -1651.466 |
This is further proof that the taxol derivative D is the most stable conformation and provides the evidence that there is a significant energy barrier between the two atropisomers of approximately 50 KJ/mol. Applying this to ΔG=-RTln(K), where now k=1.7x10-9 it can be noted that derivative D dominates in the equilibrium by a significant amount. The barrier to rotation must also be significant to allow such a dominated equilibrium and to prevent interconversion.
Analysis of the properties of the Synthesised Alkene Products (Part 2)
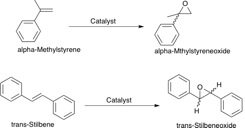

In part two the asymmetric epoxidation by two chiral catalysts for olefin containing substrates is under investigation. The Jacobsen and Shi catalysts are examined to determine how they achieve high enantiomeric excess for certain types of olefins. It is known that the Jacobsen has a high success with cis-olefins whilst the Shi catalyst yields high ee's with trans-olefins. The catalysts are depicted in the figure to the right along side the epoxidation reactions that they have been used to perform in the lab. The subsequent calculations look to provide further analysis on the reactions that have been preformed and to gain an understanding of the transition states involved.
Crystal Structure of Shi catalyst
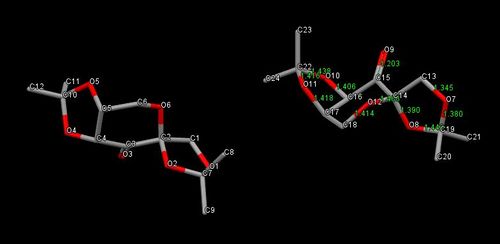
The Shi chiral catalyst contains two acetal protecting groups adjacent to the carbonyl, which are bulky enough and in the correct position to act with chiral control allowing the catalyst to yield high enantiomeric excess for certain types of alkenes. Nucleophilic attack by oxone to the carbonyl is allowed impart due to the lack of any sterically bulky groups on the five memebered rings.
| Carbon to Oxygen bond | Bond length (Å) |
|---|---|
| C(13)-O(7) | 1.345 |
| C(19)-O(7) | 1.380 (Hyperconjugation) |
| C(19)-O(8) | 1.443 (Hyperconjugation) |
| C(14)-O(8) | 1.390 (Anomeric effect) |
| C(14)-O(12) | 1.408 (Anomeric effect) |
| C(18)-O(12) | 1.414 |
| C(17)-O(11) | 1.418 |
| C(22)-O(11) | 1.416 (Hyperconjugation) |
| C(16)-O(10) | 1.406 |
| C(22)-O(10) | 1.438 (Hyperconjugation) |
The Shi catalyst is suspected of reacting asymmetrically with incoming alkenes due to steric repulsion between the methyl groups on the acetals with substituents attached to the incoming olefinic contining species. Consequently the enantioselctivity is highest for trans-disubstitued alkenes and tri-substituted alkenes. The cyclohexane ring of the Shi catalyst much like others adopts a chair conformation to minimise torsional strain. The presence of the oxygen atom in the ring provides electrons that are readily available for donation as they are less bound than electrons in NBO's. Additionally there are hetroatomic substituents adjacent to the hetroatom of the ring, which introduces the stereoelectronic effect that the adjacent substituent will occupy the axial position, this is known as the anomeric effect. This interaction places the substituents in the axial position even though this is the more hindered position due to 1,3 diaxial repulsions. Steric arguments alone are not enough and so when looking at the electronics it is observed that the best lone pair donor can overlap with the antiperiplanar C-O σ*orbital causing a greater electronic stabilising factor resluting in the alpha anomer being favoured. The more electronegative the adjacent substituent hetroatom is the greater the stabilisation and the stronger the anomeric effect is, since oxygen is the substituent here it is expected the anomeric effect is very strong. By employing Conquest and Mercury the crystal structure for the Shi catalyst has been found and the NELQEA unit cell is shown above. From the structure analysis of all C-O bond lengths has been employed. This indicates the anomeric effect is occurring as the lengths are not equivalent for all C-O single bonds. The C-O (C14-O8) of the ring is shortened due to the pi like overlap that occurs in the anomeric effect, whilst the adjacent C-O (C14-O12) becomes longer in length due to the donation of the lone pair into is antibonding orbital thus reducing its bond order. The envelope conformation of the five membered acetal ring restricts perfect antiperiplanar overlap, which prevents the lone pair on the adjacent substituent oxygen donating into the anti-bonding orbital of the fructose C-O bond. This allows the shortening and lengthening of the bonds as otherwise the two effects would cancel each other out. The C-O single bonds in the five-membered rings also participate in an electronic interaction where the lone pair of one of the oxygen atoms donates into the anti-periplanar σ*C-O orbital from the other C-O bond. This in both scenarios results in one of the bonds obtaining pi like character and thus a higher bond order, whilst the other has more anti-bonding character and has a lower bond order. Additionally these bond lengths may also be altered as a steric consequence, with the molecule attempting to minimise its energy by placing the methyl groups as far away form the molecule to prevent short contacts that would result in repulsion, this may account for the short 1.345Å C13-O7 bond. [11]
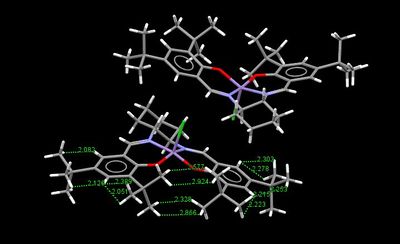
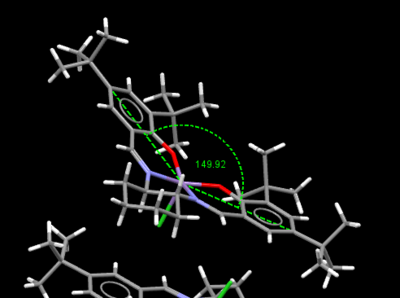
Crystal structure of Jacobsen catalyst
 |
 |
 |
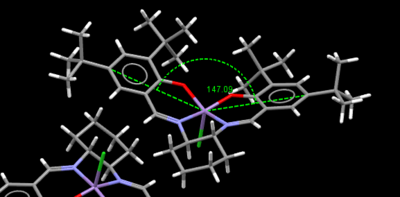 |
The Jacobsen catalyst is also a highly enantioselective chiral catalyst that yields high enantiomeric excess for cis-alkenes. The chiral component lies in the salen ligand and the the sterically bulky tert-butyl groups act to stereo-direct the incoming alkene substrate causing high enantiomeric excess to be achieved in the epoxide product, where the initial substrate is a cis-alkene. From both crystal structures above it can be seen that the ligand is distorted away from planarity, however the interaction between the tert-butyl groups mustn't be sufficiently repulsive as otherwise the structure would distort further away from planarity and distort such that the groups are further apart. This proves the distortion is to increase the attractive short contacts between H's on the t-butyl groups. When examining the distance between the tert-butyl groups, some of the hydrogen contacts lie within the Van Der Waals repulsive region (<210pm) but however there are always in both crystal structures more contacts that lie outside this region allowing an attractive interaction, which stabilises the catalyst allowing adoption of its distorted square based pyramidal shape. The difference between the two structures is if the tert-butyl groups are eclipsed or staggered. When the groups are staggered they become closer in contact, which causes increased distortion away from planarity compared to the eclipsed conformation, the angle compresses from 150 to 147°. The most important feature to notice from both crystal structures is that the close approach of the tert-butyl groups results in alkene containing molecules being blocked to enter the gap between them. The smallest gap between the groups is 2.328Å for the TOVNIOB02 unit cell and 2.818Å for the TOVNIOB01 unit cell. This then means the tert-butyl groups act as a steric barrier to prevent approach of an alkene to this face of the complex, forcing it to take an alternate approach to the catalyst. The actual approach of the alkene has somewhat been disputed and is explored in the transition state analysis section below. Although originally suggested by Jacobsen et.al. the approach of the alkene was from above the cyclohexane ring to avoid steric clashing with the t-butyl groups and possible pi-pi repulsions between the aromatic ring of the ligand and a possible aromatic ring on the substrate if a side on approach is taken. The main concept is that only one approach is favoured for cis-alkenes leading to a high enantiomeric excess for the resulting chiral epoxide [14]
NMR Analysis Of Epoxide Products
α-Methylstyreneoxide
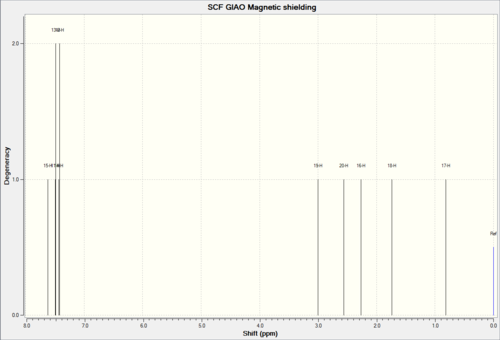 |
Computational Result (ppm) DOI:10042/26599 | Experimental Results (ppm) [15] | Deviation from literature (ppm) |
|---|---|---|---|
| 0.81 (1H) | 1.70 (3H, s) | -0.89 | |
| 1.74 (1H) | 1.70 (3H, s) | +0.04 | |
| 2.27 (1H) | 1.70 (3H, s) | +0.57 | |
| 2.56 (1H) | 2.78 (1H, d) | +0.22 | |
| 3.00 (1H) | 2.94 (1H, d) | +0.06 | |
| 7.41 (1H) | 7.15 to 7.50 (5H, m) | +0.085 | |
| 7.43 (1H) | 7.15 to 7.50 (5H, m) | +0.105 | |
| 7.48 (1H) | 7.15 to 7.50 (5H, m) | +0.155 | |
| 7.50 (1H) | 7.15 to 7.50 (5H, m) | +0.175 | |
| 7.62 (1H) | 7.15 to 7.50 (5H, m) | +0.295 |
The predicted NMR generated by computational means is in very clear alignment with literature. The main difference is that as explained earlier the calculation assumes the molecule to be stationary and so hydrogens in a methyl group that would be equivalent due to rotations become inequivalent. This can be corrected for by averaging a series of conformations of the molecule and the average chemical shift should be the value that is seen in the experimental NMR. The generated spectrum even distinguishes the terminal hydrogens to a high level of accuracy at most deviating from literature by 0.22ppm.
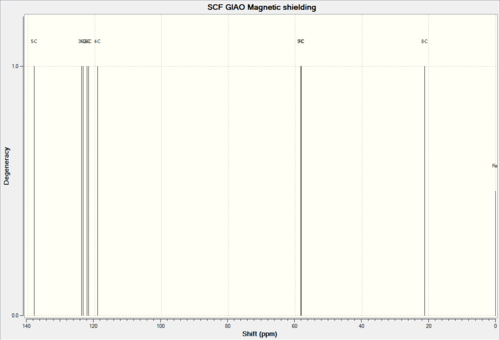 |
Computational Result (ppm) DOI:10042/26599 | Experimental Results (ppm) [16] | Deviation from literature (ppm) |
|---|---|---|---|
| 21.2 | 22.2 | -0.10 | |
| 58.1 | 57.2 | +0.09 | |
| 58.4 | 57.5 | +0.09 | |
| 119.2 | 125.7 | -6.50 | |
| 121.9 | 125.7 | -3.85 | |
| 122.4 | 127.9 | -5.50 | |
| 124.0 | 129.0 | -5.00 | |
| 138.2 | 141.6 | -3.40 |
The 13C NMR generated by computational methods deviates from literature in the aromatic region, with the largest deviation of -6.50ppm. This may be accounted for by simplification of solvent effects, where just the value of the dielectric constant may not be sufficient as the solvent can shift to preferentially sit above the aromatic rings causing a change in the magnetic environment. However this usually only corresponds to a insignificant change in the resonance signal. The most likely cause of the deviation arises due to a difference in the shielding constant between the experimental and the computational value.
trans-Stilbeneoxide
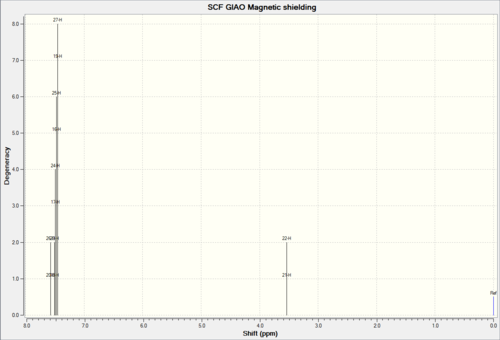 |
Computational Result (ppm) DOI:10042/26598 | Experimental Results (ppm) [17] | Deviation from literature (ppm) |
|---|---|---|---|
| 3.54 (2H) | 3.95 (2H, s) | -0.41 | |
| 7.48 (8H) | 7.40 to 7.55 (10H, m) | -0.02 | |
| 7.57 (2H) | 7.40 to 7.55 (10H, m) | +0.07 |
Again the generated NMR correlates with literature with the largest deviation by -0.41ppm. This error could be accounted for by the simplicity of the DFT basis set not accounting for the electronegativity of the oxygen atom effectively. The generated spectrum manages to differentiate the aromatic protons down to a finer level than that reported by literature by distinguishing the para position protons from the remaining protons. Further analysis had time permitted would have been to calculate the coupling values, which would have allowed a more detailed identification of the aromatic protons.
 |
Computational Result (ppm) DOI:10042/26598 | Experimental Results (ppm) [18] | Deviation from literature (ppm) |
|---|---|---|---|
| 66.4 | 63.3 | -3.1 | |
| 118.3 | 126.2 | -7.9 | |
| 123.1 | 128.8 | -5.7 | |
| 123.2 | 128.8 | -5.6 | |
| 123.5 | 128.8 | -5.3 | |
| 124.2 | 129.0 | -4.8 | |
| 134.1 | 137.6 | -3.5 |
All values correlate and have chemical shifts appropriate to their carbon environments. Small deviations between literature and the calculated NMR exist and this may be due to the static nature when calculated computationally and the high symmetry of the epoxide.
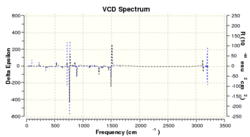
Vibrational Circular Dichromism Calculations
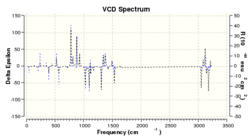
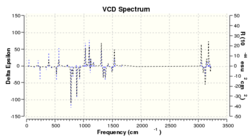
VCD spectroscopy is a powerful method in identifying enantiomers, by providing 3D structural information of the species under investigation. The technique measures the differences in attenuation of left and right circularly polarised light that passes through the sample. This therefore provides a useful method for identifying the absolute configuration of the epoxides. It also allows full determination of the structure without supporting information from other techniques. [19]
| Epoxide | VCD Spectrum DOI:10042/26598 ,DOI:10042/26599 | Epoxide | VCD Spectrum DOI:10042/26608 ,DOI:10042/26606 |
|---|---|---|---|
 |
 |
 |
|
 |
 |
 |
|
An interesting observation is that when comparing the spectrums for a pair of enantiomers the spectrum is a mirror image about the x-axis. This is to be expected as they should rotate the circularly polarised light in opposite directions as is seen in optical rotations. This can provide a great method for identification of which enantiomer has been formed providing that a spectrum has been recorded of the real sample. Unfortunately this method is not available but the spectrums have been generated out of interest and to show that simple DFT basis sets are good enough to provide a very accurate and clear VCD spectrum, which could go onto identify a product.
Optical Rotation
To be able to identify which enantiomer has been produced, a chiral shift agent (a europium based complex) could be added and NMR then preformed, otherwise NMR can only indicate connectivity and not stereochemistry. However there is a more convenient method, which is optical rotation this measures the rotation of plane polarised light as it travels through chiral species. Optical rotations can be used in conjugation with GC if mixtures of the enantiomers are present and the enantiomeric excess can be determined. If there is a racemic mixture the optical rotation is zero, as each will cancel the other out, so purification to obtain a single enantiomer is required for an accurate measurement. The optical rotation values for Methyl-styrene and trans-stilbene have been calculated using computational means and are compared to known literature values.
| Epoxide | Computational Value | Literature value |
|---|---|---|
| (R)-Methylstyreneoxide | 15.98° DOI:10042/26607 | 16° [20] |
| (S)-Methylstyreneoxide | -15.84° DOI:10042/26611 | -13° [21] |
| (R,R)-trans-Stilbeneoxide | -297.89° DOI:10042/26701 | -296° [22] |
| (S,S)-trans-stilbeneoxide | 298° DOI:10042/26615 | 296° [22] |
The data provided in the above table goes to show that the computational values are in good agreement with the literature values in both magnitude and direction. However one issue lies in the wide variety of reported values in literature for these and other epoxides. This wide range of values may arise due to a lack of obtaining an enatiopure sample in addition to the fact no standard conditions are consistently used. This problem causes any decent evaluation of the computational method to be discarded in terms of gauging the accuracy of the magnitude, but does suggest the correct direction. This can therefore be used to predict in which direction polarised light should be rotated. Finally this could also lead to a more effective why of reporting optical rotations and then comparing lab results to the computational value.
Transition State Analysis For Jacobsen and Shi Catalysts
Shi Transition State [23]
| Transition State | Sum of Electronic and Thermal Free Energies (Hartree) |
|---|---|
| (R,R)1 | -1534.687808 |
| (R,R)2 | -1534.687252 (Least stable (R,R) Transition state) |
| (R,R)3 | -1534.700037 (Most stable (R,R) Transition state and most stable overall) |
| (R,R)4 | -1534.699901 |
| (S,S)1 | -1534.68344 (Least stable (S,S) transition state and least stable overall) |
| (S,S)2 | -1534.685089 |
| (S,S)3 | -1534.693818 (Most stable (S,S) transition state) |
| (S,S)4 | -1534.691858 |
From the above table the calculations show that the transition state is the least stable for (S,S)1, which can be accounted for by the conformation of the 6-membered ring. This ring structure adopts the unstable twist boat conformation resulting in large amounts of torsional strain and poor orbital overlap stabilisation, when compared to the chair derivatives. Another feature that leads to the difference in energy of the transition states lies in whether the aromatic group of the epoxide comes into contact with substituents on the catalyst. Further more in the less stable transition states the trans-stilbene can distort from planarity, which results in a loss of pi-conjugation. As seen in the most stable transition state (R,R)3 trans-stilbene is effectively planar, the 6-membered ring of the catalyst sits in the chair conformation and the bulky aromatic groups avoid any repulsive contacts with substituents on the catalyst.
Consequently as the epoxidation has a more stable (lower energy) transition state this leads to one enantiomer being formed in excess. The enantiomeric excess can be calculated by evaluating the equilibrium constant between the most stable and the least stable transition states. To determine the equilibrium constant the free energy of the process is calculated and then used in the relation: ΔG=-RTln(K), where T is assumed to be 298K.
- Free energy, ΔG = 6.219E-3 Hartree = 16.33 KJ/mol
- Equilibrium constant, K = 1.37E-3
- Enantiomeric excess, ee = 99.9%
- lit. Enantiomeric excess, ee = 98.0% [24]
 |
|
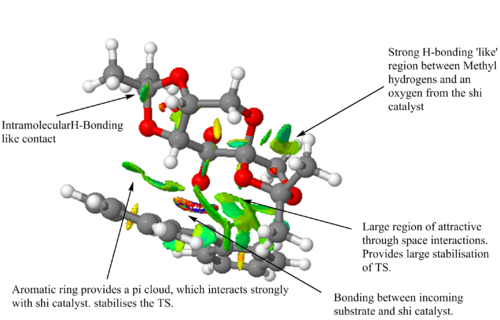
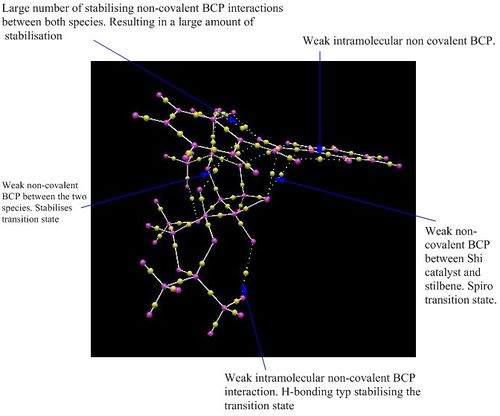
Carrying forward the most stable transition state, (R,R)3, NCI and QTAIM analysis has been performed. Both of these show the same interactions, but with the QTAIM indicating the atoms involved and the bond critical point,(BCP), involved . The NCI analysis indicates the short contacts that result in attraction or repulsion that stabilises or destabilises the transition state respectively, with the colours indicating the strength and the nature of the interaction. Blue indicates a very strong attractive interaction whilst on the other side of the spectrum red indicates strong repulsive interactions. The presence of bond formation is shown by the multi-coloured ring. Indicated by both there is a very large area of strong positive interaction, which QTAIM analysis depicts as two H-bonding like contacts between two hydrogen atoms with an oxygen atom and additionally two Van Der Waal attractive short H-H contacts. Another stabilising feature is seen in the positive interaction in the NCI analysis between a hydrogen atom and the pi system of an aromatic ring from stilbene. This short contact helps stabilise this transition state, and results in the stereo-directing of the incoming alkene and in turn helps determine the resulting stereochemistry of the epoxide. This interaction is shown in the QTAIM, which depicts the interaction between one carbon in the aromatic ring and the hydrogen of the catalyst. This may be accounted for by the fact the electrons are delocalised over all six atoms in the ring and this electron density can build up on one carbon making it extremely electron rich thus leading to a strong interaction between the two species. All the attractive interactions between the olefinic species and the catalyst result in the stabilisation of the transition state and explains why it is this enantiomer that has formed in excess. The alternate transition states occur with fewer attractive stabilising interactions and may incur destabilising interactions, which results in a high energy transition state disfavouring formation of the enantiomer that would otherwise result.
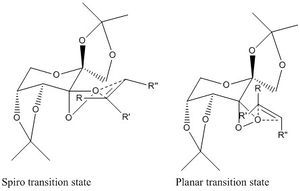
Observed from QTAIM analysis is that the transition state is spiro rather than planar. The eight possible transition states can be split into half, with one half being spiro and the other being planar. This nature determines which end of the alkene reacts with which dioxirane oxygen and therefore the resulting stereo-chemical nature of the epoxide. The most stable spiro transition state corresponds to that of the most stable (R,R) TS, whilst the most stable planar transition state belongs to the most stable (S,S) TS. With the use of the trans-disubstitued alkene, stilbene, this causes a greater favouring of the spiro transition state and hence the high enantiomeric excess achieved for this reaction. The reason for this bias is due to a favourable electronic interaction that prevails in the spiro transition state, where a secondary orbital overlap between the lone pair of a dioxirane oxygen and the pi* orbital of the alkene can overlap effectively. As noted by Shi et.al increasing the conjugation of the alkene leads to a higher enantiomeric excess, due to an increased favouring of the spiro transition state as the electronic stabilising interaction is increased for a lower energy pi* orbital.[24] The dominating product is the (R,R)enantiomer and has an 99.9% ee, this coincides with literature that also provides experimental results that confirm the(R,R)enantiomer is formed in excess with a 98.0% ee.[24]
Jacobsen Transition state [25]
| Transition State | Sum of Electronic and Thermal Free Energies (Hartree) |
|---|---|
| (S,R)1 | -3383.259559 (Most stable transition state) |
| (S,R)2 | -3383.253442 |
| (R,S)1 | -3383.25106 |
| (R,S)2 | -3383.25027 (Least Stable transition state) |
The lowest energy Jacobsen transition state with cis-β-Methylstyrene is in the formation of the (S,R) enantiomer. This is the most stable transition state as a result of the correct approach to the catalyst, which allows favourable attractive stabilising interactions. In the least stable (highest energy) transition state the approach of cis-β-Methylstyrene has its non-aromatic substituents in contact with the sterically bulky t-butyl groups. Consequently there are destabilising contacts when this approach is taken alongside the stabilising contact of the pi-pi interactions. These destabilising contacts are not present in the most stable version but the positive interactions are, thus leading to the transition energy being higher in energy and the formation of (R,S) enantiomer disfavoured. The t-butyl groups therefore stereo-direct the approach of the olefinic species leading to a high enantiomeric excess via the lowest energy transition state. As seen earlier the enantiomeric excess can be calculated.
- Free energy, ΔG = 8.499E-3 Hartree = 22.3 KJ/mol
- Equilibrium constant, K = 1.23E-4
- Enantiomeric excess, ee = 99.9%
- Lit. Enantiomeric excess, ee = 92.0% [26]
 |
|
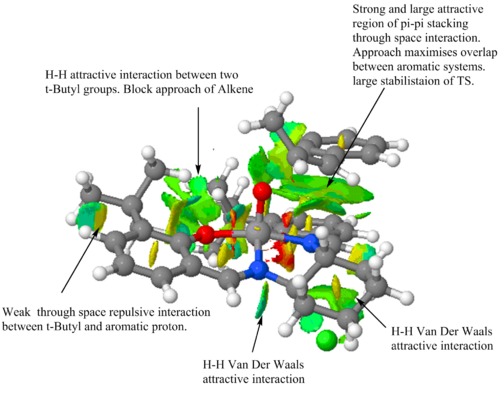
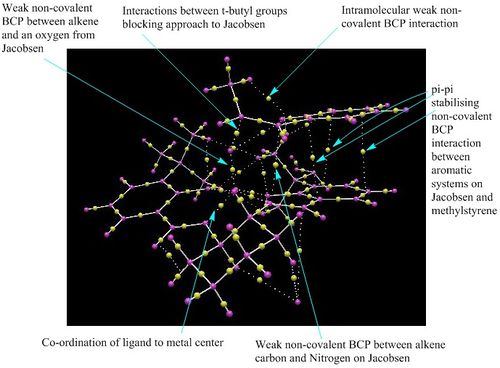
The most important feature to notice from both the NCI and QTAIM analysis is the large area of stabilising interactions. This area of interaction is a result of the effective pi-pi stacking between the aromatic groups that are on the catalyst and on methylstyrene. Consequently there is a large amount of stabilisation for this transition state which is the major contribution to the selective formation of the (S,R) enantiomer. Concentrating on the QTAIM analysis it can be observed that there are two stabilising interactions between carbons on the olefinic containing species with a nitrogen and oxygen respectively. This further stabilises the approach of the alkene and therefore lowers the energy of the transition state. QTAIM also shows the co-ordination of the ligand to the metal centre, unsurprisingly this is not a covalent bond but a weak non-covalent BCP interaction. NCI analysis indicates the attractive H-H short contacts between the t-butyl groups on the ligand that are responsible for the blocking of that trajectory to the metal-oxo species. This is also confirmed in QTAIM. These stabilising interactions strongly favour the formation of the (S,R) epoxide when cis-β-Methylstyrene is asymmetrically epoxidised by the Jacobsen catalyst.
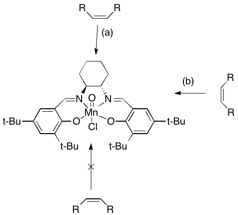
Jacobsen had initially presented the idea that the path (a) in the diagram above was the approach of the alkene that lead to high stereochemical selectivity. However Katsuki et.al suggested that trajectory (b) was the approach taken as it better accounted for the experimental observations of high enantiomeric excess for cis-alkenes, even though this was thought to have had steric repulsions from the t-butyl groups. Further analysis via computational means has confirmed this approach with research carried out by Jacobsen and Cavallo. To account for the reduced repulsions of the t-butyl groups the crystallographic data indicates that the ligand is not planar and that the catalyst is in a stepped conformation, which leads to the removal of repulsive contacts if the approach (b) is taken by the incoming alkene. This approach has been seen in the above lowest energy transition state, where the incoming cis-β-Methylstyrene sits between the cyclohexane ring and the t-butyl groups of the aromatic ring. This therefore accounts for the high enantiomeric excess observed both in literature and computationally, which only deviate by 7%, nut cagree that the major enantiomer formed is the (S,R). The highest energy transition state is destabilised due to repulsive contacts of the alkene substituents with t-butyl groups as it takes an approach such that these come into the repulsive Van Der Waals region. [26],[27]
An Alternate Alkene For Asymmetric Epoxidation
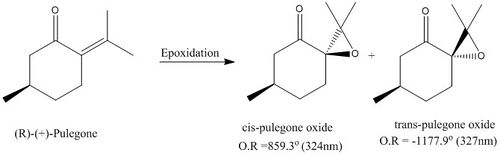
An alternative candidate for investigation is R-(+)-pulegone. This alkene is readily available from sigma Aldrich and would allow the effect of the alkene being part of an enone to be explored. The resulting ee could be examined and further transition state analysis could be performed to note the effect of the carbonyl. The resulting epoxide products have an optical rotation with magnitude greater than |500°|, with a value reported in literature of 859.3°(324nm) and -1177.9°(327nm) respectively and at room temeperature Also seen from current literature preformed on this alkene, is that epoxidation with m-CPBA is insufficent due to the elctron deficient nature of the alkene so H2O2 with sodium hydroxide is used to form the epoxide. It will be interesting to note if altered conditions are also required when using the Jacobsen or Shi chiral catalysts.[28] [29]
References
- ↑ J. Sauer, R. Sustmann, Angew. Chem. Int. Ed. Engl., 1980, 19, 779 - 807 DOI:10.1002/anie.198007791
- ↑ K. Alder, G. Stein , Angew. Chem., 1937, 50, 510 DOI:10.1002/ange.19370502804 10.1002/ange.19370502804
- ↑ D. Skala, J. hanika, Petroleum and Coal 45, 3-4, 105-108
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0
- ↑ Bringmann G, Mortimer AJP, Keller PA, Gresser MJ, Garner J, Breuning M (2005). "Atroposelective Synthesis of Axially Chiral Biaryl Compounds". Angewandte Chemie International Edition 44 (34): 5384–5427. DOI:10.1002/anie.200462661
- ↑ J. Clayden, N.Greeves, S. Warren and P. Worthers, Chapter 18, Conformational Analysis, p. 452-471, OUP Oxford
- ↑ Shea, K. (1980). "Recent developments in the synthesis, structure and chemistry of bridgehead alkenes". Tetrahedron 36 (12): 1683–1715. DOI:10.1016/0040-4020(80)80067-6.
- ↑ Camps, P., Pujol, X., Vázquez, S., Pericàs, M. A., Puigjaner, C., & Solà, L. (2001). Cross-coupling of a functionalized highly pyramidalized alkene: DSC and NMR study of the [2+ 2] retrocycloaddition of cyclobutane cross products, hyperstability and pyramidalization of the formed dienes. Tetrahedron, 57(40), 8511-8520
- ↑ 9.0 9.1 Spectroscopic data: L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043
- ↑ M.Durik, V.Langer, D.Gyepesova, J.Micova, B.Steiner, M.Koos, Acta Crystallogr.,Sect.E:Struct.Rep.Online (2001), 57, o672, DOI:10.1107/S160053680101073X
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (1996) "Anomeric Effect".
- ↑ 12.0 12.1 J.W.Yoon, T.-S.Yoon, S.W.Lee, W.Shin, Acta Crystallogr.,Sect.C:Cryst.Struct.Commun. (1999), 55, 1766, DOI:10.1107/S0108270199009397
- ↑ 13.0 13.1 F.R.Fronczek, X.R.J.Bu, Private Communication (2002)
- ↑ McGarrigle, EM; Gilheany, DG (2005). "Chromium- and Manganese-salen Promoted Epoxidation of Alkenes". Chem. Rev. 105 (5): 1563–1602. DOI:10.1021/cr0306945
- ↑ Connon, Stephen J.; Kavanagh, Sarah A.; Piccinini, Alessandro Advanced Synthesis and Catalysis, 2010 , 352, # 11-12 p. 2089 - 2093 DOI:10.1002/adsc.201000255.
- ↑ Buckle, Richard; Davies, A. Matthew; Graham, Andrew E.; Mabbett, Ian; Robinson, Mathew W. C.; Taylor, Stuart H. Organic and Biomolecular Chemistry, 2009 , 7, 12 p. 2559 - 2564 DOI:10.1039/b900719a.
- ↑ Graham, Andrew E.; Kean, Joseline L.; Phillips, David J. Tetrahedron, 2013 , 69, # 30 p. 6196 - 6202 DOI:10.1016/j.tet.2013.05.036.
- ↑ Buckle, Richard; Davies, A. Matthew; Graham, Andrew E.; Mabbett, Ian; Robinson, Mathew W. C.; Taylor, Stuart H. Organic and Biomolecular Chemistry, 2009 , 7, 12 p. 2559 - 2564 DOI:10.1039/b900719a.
- ↑ R. K. Dukor and L. A. Nafie, in Encyclopedia of Analytical Chemistry: Instrumentation and Applications, Ed. R. A. Meyers (Wiley, Chichester, 2000) 662-676.
- ↑ Lin, Hui; Liu, Yan; Wu, Zhong-Liu; Lin, Hui Tetrahedron Asymmetry, 2011 , 22, # 2 p. 134 - 137 DOI:[1]
- ↑ Andres, Celia; Infante, Rebeca; Nieto, Javier. Chemistry - A European Journal, 2012 , 18, 1 p. 4375 - 4379 DOI:10.1002/chem.201102913.
- ↑ 22.0 22.1 Diep-Vohuule, Anh; Solladie-Cavallo, Arlette; Sunjic, Vitomir; Vinkovic, Vladimir, Tetrahedron Asymmetry, 1996 , 7, # 6 p. 1783 - 1788 DOI:10.1016/0957-4166(96)00213-3.
- ↑ Rzepa, Henry S. (2013): Gaussian Job Archive for C26H30O7. figshare.DOI:/10.6084/m9.figshare.829522
- ↑ 24.0 24.1 24.2 Y. Shi, "Organocatalytic Asymmetric Epoxidation of Olefins by Chiral Ketones", Acc. Chem. Res., 2004, 37 (8), 488-496. DOI:10.1021/ar030063x
- ↑ Rzepa, Henry S. (2013): Gaussian Job Archive for C37H46ClMnN2O3. figshare. DOI:/10.6084/m9.figshare.740436
- ↑ 26.0 26.1 E. N. Jacobsen, W. Zhang, A. R. Muci, J. R. Ecker, L. Deng "Highly Enantioselective Epoxidation Catalysts Derived from 1,2-Diaminocyclohexane", J. Am. Chem. Soc., 1991, 113, 7063-7064. DOI:10.1021/ja00018a068
- ↑ T. Linker, Angew. Chem. Int. Ed., 1997, 36, 2060. DOI:10.1002/anie.199720601
- ↑ W. Reusch and C. K. Johnson Journal of Organic Chemistry, 1963 , 28, p. 2557-2560 DOI:10.1021/jo01045a016
- ↑ US Department of Health and Human Services, NTP Technical Report on the Toxicology and Carcinogenesis - Studies of Pulegone, 2011.