Bond Dissociation Energies

The bond dissociation energy, (BDE), is a measure of the strength of a chemical bond. In this investigation the BDE will be used to determine the strength of dative covalent bonds in a series of molecules. Computational calculations will determine the energy minimum for the molecules that combine to form these dative bonds and also the energy of the final molecules. By using the following formula the BDE can be calculated:

Association energy ΔE = E(R₃EMR₃) - [E(R₃E) + E(MR₃)]
BDE = -Association energy

A dative covalent bond is a type of 2-electron 2-center covalent bond, where the two electrons are donated from one species ^[1]. This species is represented as R₃E and is a lewis base, whilst the species that accepts the electron pair is shown as MR₃ and is a lewis acid. The series of molecules chosen will explore the effect of the bond strength as the ability of lone pair donation changes and as the ability of lone pair acceptance alters with different strengths. The lewis acids selected are BH₃ and AlH₃, these molecules will note the ability of accepting a lone pair of electrons upon descending down a group with increasing orbital size. The lewis bases used are to explore the effects of electronegativity on lone pair donation and are NH₃ and PH₃.

Lewis adduct molecules with a dative covalent bond used to determine BDE as a function of lone pair donation and lone pair acceptance:
1) NH₃BH₃
2) NH₃AlH₃
3) PH₃BH₃
4) PH₃AlH₃

NBO analysis will also be preformed to see what the charge distribution is within the lewis adduct species. This will show how the charges carried by an atom change on accepting or donating a lone pair of electrons. To achieve this the charge distribution will be compared from when the species is free to when it binds to from the dative bond. Enhancing the analysis further, calculation of the difference in the HOMO-LUMO energy gap between the donor and acceptor species will be quantified and the effects of orbital overlap and splitting energy will be discussed. As a consequence of all of these factors the strength of the dative covalent bond between the following molecules will alter and will be measured and rationalised by computational methods.

Optimisation and Frequency Analysis

To optimise the molecules a 6-31G basis set was employed with a RB3LYP calculation method. This is constant for all molecules to allow comparison of energy between the structures. Frequency analysis has been carried out to ensure the molecules are at a minimum. This was completed by using the same basis set and calculation method but with the calculation type changed to frequency.

BH₃

BH₃ 6-31G (d,p) optimisation: Media:BH3-OPT-631G.LOG

Table of BH₃ 6-31G(d.p) optimisation parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-26.61532363 au
Gradient	0.00000235 au
Dipole moment	0.00D
Point group	D_3h
Calculation time	57 Seconds
Bond length	1.192 Å
Bond angle	120.0^o

 Item Value Threshold Converged?
 Maximum Force 0.000005 0.000450 YES
 RMS Force 0.000003 0.000300 YES
 Maximum Displacement 0.000019 0.001800 YES
 RMS Displacement 0.000012 0.001200 YES
 Predicted change in Energy=-1.305135D-10
 Optimization completed.
  -- Stationary point found.

BH₃ Vibrational analysis summary: Media:NPA-BH3-OPT-631G-VA.LOG

Table of BH₃ Vibrational analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-26.61532363 au
Gradient	0.00000237 au
Dipole moment	0.00D
Point group	D_3h
Calculation time	16 Seconds

Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824
Low frequencies --- 1163.0003 1213.1853 1213.1880

AlH₃

AlH₃ 6-31G (d,p) optimisation: Media:NPA_ALH3_OPT.LOG

Table of AlH₃ 6-31G(d.p) optimisation parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-244.20693892 au
Gradient	0.00007439 au
Dipole moment	0.00D
Point group	D_3h
Calculation time	57 Seconds
Bond length	1.587 Å
Bond angle	120.0^o

 Item Value Threshold Converged?
Maximum Force 0.000149 0.000450 YES
RMS Force 0.000097 0.000300 YES
Maximum Displacement 0.001049 0.001800 YES
RMS Displacement 0.000686 0.001200 YES
Predicted change in Energy=-2.160762D-07
Optimization completed.
-- Stationary point found.

AlH₃ Vibrational analysis summary: Media:NPA_ALH3_FREQ.LOG

Table of BH₃ Vibrational analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-244.20693892 au
Gradient	0.00007432 au
Dipole moment	0.00D
Point group	D_3h
Calculation time	24 Seconds

Low frequencies --- -0.0899 -0.0068 -0.0021 33.0152 34.6861 34.6861
Low frequencies --- 708.2605 791.3120 791.3128

NH₃

In the keywords section "nosymm" to increase the accuracy of the optimisation.

NH₃ 6-31G(d,p) optimisation:Media:NH3_OPTIMISATION.LOG

Table of NH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-56.55776856 au
Gradient	0.00000885 au
Dipole moment	1.85D
Point group	C1
Calculation time	1 minute 59 Seconds

 Item Value Threshold Converged?
Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629715D-09
 Optimization completed.

-- Stationary point found.

NH₃ Frequency analysis:Media:NPA_NH3_FREQ.LOG

Table of NH₃ Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-56.55776856 au
Gradient	0.00000887 au
Dipole moment	1.85D
Point group	C1
Calculation time	28 Seconds

Low frequencies --- -30.7927 -0.0010 -0.0008 0.0011 20.2690 28.2324
Low frequencies --- 1089.5544 1694.1237 1694.1863

PH₃

PH₃ 6-31G(d,p) optimisation:Media:NPA_PH3_OPT.LOG

Table of NH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-343.14506772 au
Gradient	0.00009247 au
Dipole moment	0.96D
Point group	C3V
Calculation time	1 minute 54 Seconds

  Item Value Threshold Converged?
Maximum Force            0.000140     0.000450     YES
 RMS     Force            0.000092     0.000300     YES
 Maximum Displacement     0.000506     0.001800     YES
 RMS     Displacement     0.000353     0.001200     YES
 Predicted change in Energy=-1.316361D-07
 Optimization completed.
-- Stationary point found.

PH₃ Frequency analysis:Media:NPA_PH3_FREQ.LOG

Table of PH₃ Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-343.14506772 au
Gradient	0.00009259 au
Dipole moment	0.96D
Point group	C3V
Calculation time	49 Seconds

Low frequencies --- -39.8181 -39.8007 -35.7096 -0.0034 0.0445 0.1171
 Low frequencies --- 1036.3447 1155.1671 1155.1671

NH₃BH₃

6-31G(d,p) Optimisation of NH₃BH₃ : Media:NPA_NH3BH3_FREQ.LOG

Table of NH₃BH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-83.22468924 au
Gradient	0.00002095 au
Dipole moment	5.56D
Point group	C1
Calculation time	22 Seconds

Item Value Threshold Converged?
Maximum Force            0.000037     0.000450     YES
 RMS     Force            0.000015     0.000300     YES
 Maximum Displacement     0.000540     0.001800     YES
 RMS     Displacement     0.000242     0.001200     YES
 Predicted change in Energy=-2.237685D-08
 Optimization completed.

-- Stationary point found.

Frequency analysis of NH₃BH₃ : Media:NPA_NH3BH3_FREQ1.LOG

Table of NH₃BH₃ 6-31G Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-83.22468924 au
Gradient	0.00002095 au
Dipole moment	5.56D
Point group	C1
Calculation time	63 Seconds

Low frequencies --- -11.2042 -0.0008 -0.0004 0.0011 12.2537 14.9711
Low frequencies --- 263.0537 632.9047 638.0070

NH₃AlH₃

6-31G(d,p) Optimisation of NH₃AlH₃ :Media:NPA_NH3ALH3_OPT.LOG

Table of NH₃AlH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-300.81503249 au
Gradient	0.00001437 au
Dipole moment	5.68D
Point group	C1
Calculation time	3 minuutes 58 Seconds

 Item Value Threshold Converged?
Maximum Force            0.000027     0.000450     YES
 RMS     Force            0.000011     0.000300     YES
 Maximum Displacement     0.000355     0.001800     YES
 RMS     Displacement     0.000096     0.001200     YES
 Predicted change in Energy=-1.592939D-08
 Optimization completed.

-- Stationary point found.

Frequency analysis of NH₃AlH₃ :Media:NPA_NH3ALH3_FREQ.LOG

Table of NH₃AlH₃ 6-31G Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-300.81503249 au
Gradient	0.00001442 au
Dipole moment	5.68D
Point group	C1
Calculation time	1 minute 13 Seconds

Low frequencies --- -16.1692 0.0044 0.0047 0.0048 4.3269 9.8718
 Low frequencies --- 123.9870 378.8048 379.3829

PH₃BH₃

6-31G(d,p) Optimisation of PH₃BH₃ :Media:NPA_PH3BH3_OPT.LOG

Table of PH₃BH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-369.79375989 au
Gradient	0.00004238 au
Dipole moment	4.07D
Point group	C1
Calculation time	7 minuutes 59 Seconds

  Item Value Threshold Converged?
Maximum Force            0.000065     0.000450     YES
 RMS     Force            0.000036     0.000300     YES
 Maximum Displacement     0.001153     0.001800     YES
 RMS     Displacement     0.000330     0.001200     YES
 Predicted change in Energy=-1.587882D-07
 Optimization completed.

-- Stationary point found.

Frequency analysis of PH₃BH₃ :Media:NPA_PH3BH3_FREQ.LOG

Table of PH₃BH₃ 6-31G Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-369.79375980 au
Gradient	0.00004251 au
Dipole moment	4.07D
Point group	C1
Calculation time	1 minute 20 Seconds

Low frequencies --- -15.5797 -0.0033 -0.0020 -0.0010 5.0951 8.2108

Low frequencies --- 246.3995 385.3693 385.5773

PH₃AlH₃

6-31G(d,p) Optimisation of PH₃AlH₃ :Media:NPA_PH3ALH3_OPT.LOG

Table of PH₃AlH₃ 6-31G Optimisation analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-587.37368137 au
Gradient	0.00004256 au
Dipole moment	4.28D
Point group	C1
Calculation time	5 minuutes 21 Seconds

 Item Value Threshold Converged?
Maximum Force            0.000101     0.000450     YES
 RMS     Force            0.000045     0.000300     YES
 Maximum Displacement     0.001765     0.001800     YES
 RMS     Displacement     0.000675     0.001200     YES
 Predicted change in Energy=-2.856398D-07
 Optimization completed.

-- Stationary point found.

Frequency analysis of PH₃AlH₃ :Media:NPA_PH3ALH3_FREQ.LOG

Table of PH₃AlH₃ 6-31G Frequency analysis parameters and results
Summary Information	Result
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-587.37368177 au
Gradient	0.00004259 au
Dipole moment	4.28D
Point group	C1
Calculation time	1 minute 15 Seconds

 Low frequencies --- -17.4735 -0.0018 0.0022 0.0022 0.7856 2.3128
 Low frequencies --- 127.8760 220.5775 221.3959

NBO Analysis

NBO analysis has been preformed by taking the .chk file of the optimisation and changing the method type to energy and adding "pop=full" in the additional key words and under the NBO tab full NBO was selected. All results are then taken from the .log file of this population calculation. The NBO's show the charge distribution of the molecule, this will provide information on how donated the lone pair is and how accepted the lone pair is by the lewis acid in comparison to the charge carried by the respective free molecules.

NH₃ NBO

NH₃ NBO analysis:Media:NPA_NH3_MO.LOG

Charge distribution for NH₃ with charge limits -1.0 to +1.0

Table of NH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-56.55776856 au
Gradient	0.0000000 au
Dipole moment	1.85D
Point group	C1
Calculation time	37 Seconds

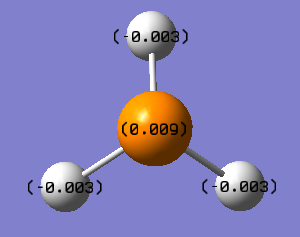
PH₃ NBO

PH₃ NBO analysis:Media:NPA_PH3_MO.LOG

Charge distribution for PH₃ with charge limits -1.0 to +1.0

Table of PH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-343.14506772 au
Gradient	0.0000000 au
Dipole moment	0.96D
Point group	C3V
Calculation time	6 Seconds

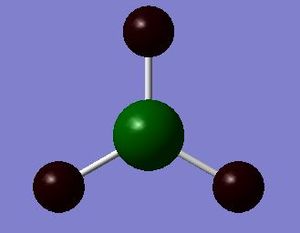
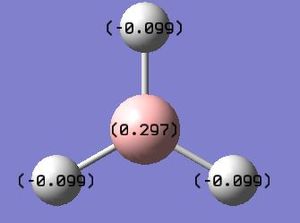
BH₃ NBO

BH₃ NBO analysis :Media:NPA_BH3_MO.LOG

Table of BH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-26.61532363 au
Gradient	0.0000000 au
Dipole moment	0.00D
Point group	D3h
Calculation time	6 Seconds

AlH₃ NBO

AlH₃ NBO analysis :Media:NPA_ALH3_MO.LOG

Table of AlH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-244.20693892 au
Gradient	0.0000000 au
Dipole moment	0.00D
Point group	D3h
Calculation time	7 Seconds

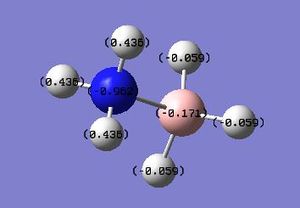
NH₃BH₃ NBO

NH₃AlH₃ NBO analysis :Media:NPA_NH3BH3_MO.LOG

Table of NH₃BH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-83.22468924 au
Gradient	0.0000000 au
Dipole moment	5.56D
Point group	C1
Calculation time	8 Seconds

NH₃AlH₃ NBO

NH₃BH₃ NBO analysis :Media:NPA_NH3ALH3_MO.LOG

Table of NH₃BH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-300.81503249 au
Gradient	0.0000000 au
Dipole moment	5.68D
Point group	C1
Calculation time	8 Seconds

PH₃BH₃ NBO

PH₃BH₃ NBO analysis :Media:NPA_PH3BH3_MO.LOG

Charge distribution for PH₃BH₃ with charge limits -1.0 to +1.0

Table of PH₃BH₃ Molecular Orbitals parameters and results
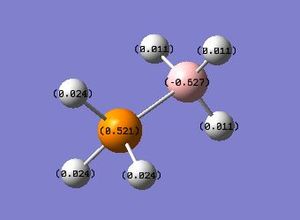
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-369.79375989 au
Gradient	0.0000000 au
Dipole moment	4.07D
Point group	C1
Calculation time	6 Seconds

PH₃AlH₃ NBO

PH₃AlH₃ NBO analysis :Media:NPA_PH3ALH3_MO.LOG

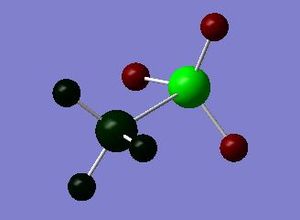
Table of PH₃AlH₃ Molecular Orbitals parameters and results
Summary Information	Result
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-587.37368147 au
Gradient	0.0000000 au
Dipole moment	4.28D
Point group	C1
Calculation time	7 Seconds

Percentage Contribution to E-M Dative Bond

Percentage contribution from P, N, B and Al to the E-M dative bond.
Moleclue	Boron	Aluminium	Nitrogen	Phosphorus
NH₃BH₃	18.18%	-	81.88%	-
NH₃AlH₃	-	7.81%	92.19%	-
PH₃BH₃	33.93%	-	-	66.07%
PH₃AlH₃	-	12.63%	-	87.37%

The above table shows the percentage contribution from each atom to the dative covalent bond. It indicates that as the size of the acceptor orbital increases the percentage it contributes to the dative bond decreases. This is noted in the BDE of the bonds with the species containing aluminium having lower values, weaker bonds, than those containing boron in its place. Additionally it shows that ammonia contributes more to the formation of the dative bond than phosphine. This indicates that although phosphorus is a better lone pair donor that there are orbital overlap and splitting enrgy considerations such as diffusivity, orbital size, relative location and orientation. These factors are what cause the BDE to be higher in the ammonia containing lewis adducts.

MO Analysis of the dative covalent bond

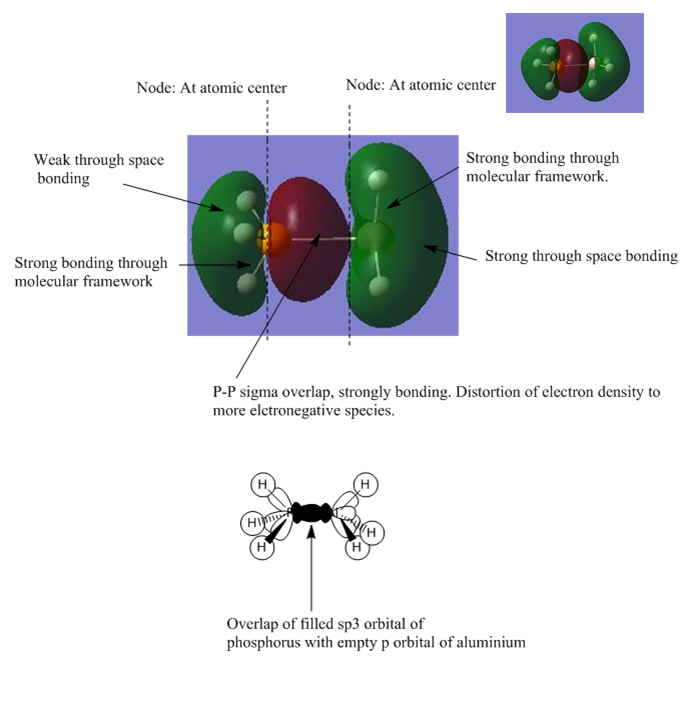
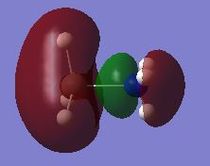
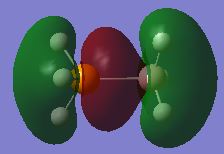
The MO shows the bonding orbital that forms due to the overlap of the donor orbital with the acceptor orbital. In all cases the donor orbital is a filled sp³ orbital and the acceptor orbital is an empty p-orbital as depicted in the LCAO model. This overlap corresponds to a strongly bonding interaction and leads to a large amount of electron density between the two species corresponding to the formation of the dative bond. This bond is polarised towards the most electronegative species as shown in the MO's with the electron distribution shifted towards the phosphorus or the nitrogen. The weak through space bonding interaction arises due to overlap between the three s-sp³ overlaps that form when the orbitals of the donor atom overlap with its adjacent hydrogen atoms' s orbitals. The node at the atomic center is not as important as a node between different bonding orbitals, as the latter causes anti-bonding character and causes destabilisation of the molecular orbital. However for a node at the center this effect is not as prominent as it has no effect on bonding and therefore has no effect on the relative energy of the MO. The strong bonding through the molecular framework is due to overlap between s orbitals from hydrogen and sp orbitals from both donor and acceptor species. In the donor systems it is an sp³ orbital, whilst in the acceptor species its an sp². The acceptor side of the lewis adduct has stronger through space interactions as a result of the empty p-orbital having constructive interference with the three bonding orbitals that arise form the sp² orbital overlaping with the s orbitals on hydrogen. These factors all lead to this MO being strongly bonding and shows the LCAO that will result in the dative bond being formed. The extent to which this MO is stabilised and hence how strong the dative bond is will depend on the orbital overlap of the filled sp3 orbital from the donor with the empty p orbital of the acceptor.

Results and Discussion

To calculate the BDE, firstly the association energy is calculated by using the formula stated earlier and then the negative of this number corresponds to the BDE. The larger the value of the BDE the stronger the dative covalent bond is. In the molecules examined the calculation is simple once the energies of the respective components have been determined with the initial value determined in au and then converted into kJ/mol. The strength of the dative bonds are presented below.

Table of calculated data from compuational calculations
Molecule	BDE (kJ/mol)	Charge Distribution
Molecule	BDE (kJ/mol)	N	P	H_a	B	Al	H_d
NH₃BH₃	+135.4	-0.962	-	+0.436	-0.171	-	-0.059
NH₃AlH₃	+132.1	-1.154	-	+0.436	-	+0.962	-0.372
PH₃BH₃	+87.6	-	+0.521	+0.024	-0.627	-	+0.011
PH₃AlH₃	+56.9	-	+0.100	+0.041	-	+0.804	-0.342
NH₃	-	-1.125	-	+0.375	-	-	-
PH₃	-	-	+0.009	-0.003	-	-	-
BH₃	-	-	-	-	+0.297	-	-0.099
AlH₃	-	-	-	-	-	+1.135	-0.372

It is expected that phosphorus would be a better lone pair donor than ammonia due to its lower electronegativty of 2.19 compared to that of nitrogen at 3.04 allowing the lone pair to be held less tightly. NBO analysis has proven this to be the case however the BDE indicates that there are also more factors than just lone pair donation that effect the strength of the dative bond as the PH₃ containing lewis adducts have weaker bonds than those containing NH₃. The table above shows the NBO charge distributions for their respective molecules and indicates the donation and acceptance effects on changing the lewis acid and base.^[2]

The electronegativity of nitrogen in ammonia results in a large negative charge build up on the atom. Having the a large negative charge and the elctronegativity of nitrogen I expected the lone pair to be held tightly and less available for donation. This actually means the lone pair can be donated to form strong bonds due to it having directionality and being localized in a small orbital. The orbital has a high electron density, which favours formation of strong bonds.

The phosphorous atom in phosphine is less electronegative than the hydrogen atoms and therefore carries a positive charge. This results in the lone pair of phosphine being held less tightly than in ammonia. Therefore it should be expected that phosphine donates its lone pair more easily, which could result in stronger dative covalent bonds. However orbital overlap factors, which will be explored later, cause the phosphine ligand to form weaker than expected dative bonds.

Boron is more electropositive than hydrogen in borane and it is therefore expected that the hydrogens are hydridic and carry a negative charge. The positive charge carried by boron accounts for its ability to accept lone pairs as it is electron deficient and carries an empty orthogonal p-orbital.

Similar to boron aluminium is electropositive, which results in the hyrdrogens carrying a negative charge. The difference in magnitude of values arises in the fact that electropositivity increases down a group and therefore aluminium will have a greater positive charge than boron. However its strength as a lewis acid is hindered by its orbital size leading to poorer overlap.

In the NH₃BH₃ adduct nitrogen is the most electronegative and thus carries the largest negative charge. Boron gains a negative charge as the nitrogen lone pair has donated into the empty p-orbital causing it to carry negative charge even though boron is an electropositive element. The nitrogen atom distorts the electron density towards itself again accounted by its high electronegativty. The hydrogens attached to nitrogen carry a positive charge again accounting from the electronegativity of nitrogen pulling electron density towards itself. Similar to free borane the hydrogens are hydridic because of the electropositivity of boron.

For NH₃AlH₃ the electronegativity of the nitrogen compared to hydrogen determines the negative charge of the nitrogen atom and the positive charge of the adjacent hydrogen atoms. The aluminium has a positive charge still where as boron had obtained a negative charge, this is because the aluminium is less effective at obtaining electron density from the donating amine. However this positive charge is reduced from that of free AlH₃ due to the fact that there is some lone pair donation effects from the adjacent nitrogen atom.

Phosphorus gains a larger positive charge in PH₃BH₃ than in free PH₃ because the lone pair is now being donated into an empty orbital, which removes electron density away from the atom. The three hydrogens attached to the phosphorus atom have a positive charge due to the phosphorus pulling electron density away as it has gained a positive charge. Boron acquires a negative charge due to the acceptance of the lone pair into its empty orbital. The magnitude of this negative charge is greater than when the donor is ammonia, further proving that the lone pair is better donated by the phosphorus atom than the nitrogen atom. The remaining hydrogens are positive as a consequence of boron accepting electron density efficiently from phosphorus and acquiring a negative charge.

In PH₃AlH₃ the lewis acidity of aluminium causes the phosphorous to donate its electron pair efficiently and also results in the phosphorus pulling electron density away from its attached hydrogen atoms causing them to carry a positive charge. The aluminum carries a less positive charge than in free AlH₃ as explained by the extra electrons gained by donation from the lone pair on phosphorus. As seen previously, the resulting positive charge on aluminium is less than that in NH₃AlH₃ reinforcing that the phosphorus atom is better at donating its electrons causing the charge to decrease on the acceptor atom more than when the nitrogen atom donates. The adjacent hydrogens to aluminium carry a negative charge similar to those in free AlH₃ due to the electropositivty of aluminium resulting in them being hydridic. This is further proof that the aluminium is less effective at accepting lone pairs as the value is still positive, whilst the value of boron in PH₃BH₃ has become negative as it has accepted the electrons efficiently.

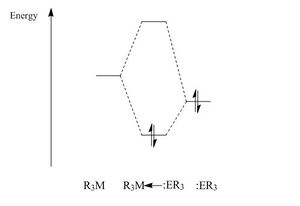
To rationalise the BDE of the molecules, the orbital overlap must be explored. This is because bond strength is heavily dependent on orbital overlap and the splitting energy, the better the overlap the stronger the bond. The quality of orbital overlap is shown in quantum mechanical equations as the overlap integral, S_ij, this depends on the relative location, orientation and diffusivity of the orbitals involved. Additionally the splitting energy also depends on how close in energy the interacting HOMO and LUMO orbitals are. If they are close in energy they have a good overlap leading to strong bonds. It also depends on orbital size; larger orbitals have poorer overlap and thus cause weaker bonds to be formed. Presented below are the energies of the HOMO and LUMO of each component. These values can then determine the energy difference for each of the lewis adduct molecules showing which molecule has the best orbital overlap.

Energy of HOMO and LUMO orbitals
Molecular orbital	MO energies
Molecular orbital	NH₃	PH₃	BH₃	AlH₃
HOMO	-0.25317	-0.27508	-0.35079	-0.30635
LUMO	0.07985	0.03268	-0.06605	-0.07118

These results suggest that the LUMO of AlH₃ is lower in energy than that of BH₃. According to theory this seems anomalous as orbital energy increases down a group. The LUMO orbital in both of these molecules is the non-bonding a2"orbital, which is the empty orthogonal p-orbital. From the results collected this places the 3p orbital lower in energy than the 2p orbital. This implies there are greater electronic effects that are taken into account by computational quantum calculations. Furthermore it would have been predicted that the NH₃ HOMO orbital would have been lower in energy than the HOMO of PH₃ as in MO theory the more electronegative a species is the lower its orbital energy. The following table shows the values of the difference in energy of the HOMO and LUMO orbitals of the respective components that combine to make the lewis adduct species. The HOMO orbital comes from the donor species, whilst the LUMO orbital comes from the acceptor species.

Energy gap between HOMO and LUMO
Molecule	Energy difference
NH₃BH₃	0.18712
PH₃BH₃	0.20903
NH₃AlH₃	0.18199
PH₃AlH₃	0.20390

The main trend to be observed from this data is that on changing the donor species from NH₃ to PH₃ the energy gap of the HOMO and LUMO increases. This means that although the donor ability has increased the splitting energy will have decreased resulting in the covalent bond formed being less stabilised and weaker. Hence when looking at the BDE's it is observed that the phosphorus containing species have the lowest values and therefore have the weakest bonds. The difference between changing the acceptor species has a small effect on the difference in the energy gap. As the values are close this means the splitting energy is approximately the same and so therefore the difference in BDE must be attributed to another factor of orbital overlap. Further studies could be performed to determine this, however looking at the other factors that affect orbital overlap the BDE order can be rationalised. So even though NH₃BH₃ has a slightly larger energy gap than NH₃AlH₃ the orbital size of aluminium is larger than that of boron due to their respective positions in the periodic table and thus leads to poorer orbital overlap and therefore weaker bonds are produced. The diffusivity of the orbitals is also another important contributing factor and reinforces why ammonia forms stronger dative bonds than phosphine as the lone pair is highly concentrated in a smaller orbital giving rise to a highly dense orbital, which leads to strong overlap. Orientation is negligible as it is similar lobes overlapping in all lewis adducts. Finally the relative position location has an effect on the orbital overlap, the closer they are in space the better the overlap. This is prominent in the BDE as the strongest bond is between the smallest donor and acceptor as this results in the orbitals being closer. At the opposite end of this the species with the weakest BDE is constructed from the largest donor and acceptor resulting in the orbitals being further away leading to poorer overlap and thus having the weaker dative bond.

Supporting evidence of the importance of the orbital overlap is shown in the final bond angle of the lewis acid species once it combines to form the adduct. As the lewis acid accepts a pair of electrons its geometry distorts from trigonal planar to tetrahedral. The pseudo symmetry of the acid changes from D_3h to C_3v. This results in a bond angle change that depends on how good the orbital overlap is and the bond distance.

Bond angle of lewis acid in lewis adduct molecules
Molecular orbital	Bond angle		E-M Bond length
Molecular orbital	BH₃	AlH₃
NH₃BH₃	113.9°	-	1.67Å
PH₃BH₃	114.8°	-	1.96Å
NH₃AlH₃	-	117.5°	2.10Å
PH₃AlH₃	-	118.6°	2.38Å

Observed from this trend is that the orbital overlap between ammonia and borane is effective and results in the lewis acid gaining a greater tetrahedral character. From NBO analysis it is known that PH₃ is a better lone pair donor and it would be expected that the distortion would be greater however in PH₃BH₃ the bond angle is larger. This can be attributed to the increase in bond length, which allows reduced steric interactions between the hydrogens across the dative bond thus the hydrogens don't distort as far. This is also reinforced in the bond angles of NH₃AlH₃ compared to PH₃AlH₃. The effect of changing the lewis acid from BH₃ to AlH₃ results in larger bond angles as aluminium has larger, more diffuse orbitals, which means it accepts electron density poorly and hence the distortion to tetrahedral is less.

Conclusion

In conclusion the BDE of the dative bonds in the series of lewis adduct molecules tested depends on two factors. These factors are donor/acceptor ability and orbital overlap. From the NBO analysis it has been shown that the phosphine ligand is better at donating electrons than the ammonia ligand. This was due to the fact that nitrogen is more electronegative than phosphorus and therefore holds its electron pair more tightly making them less available for donation. This is observed by the increase in electron density on both boron and aluminium when they are bonded to PH₃. Additionally NBO analysis proved that borane was the better acceptor as the electron density gained was larger than that of aluminium when either borane or phosphine were donating and this is to be expected as it is more lewis acidic. If this was the only factor then the BDE order would be different to what has been calculated so the other factor must play a large part in the strength of the resulting dative bond.

To rationalise the determined values of the BDE orbital overlap must be considered. Analysis of the energy gap between the HOMO and LUMO of the donor and acceptor respectively showed some interesting results. It showed that PH₃ lead to the largest energy gap between the HOMO and LUMO orbitals. This suggests that the splitting energy is less and therefore the dative bond formed is stabilised less effectively and results in weaker bonds than first expected from NBO analysis alone. What was strange was the order of the LUMO orbital when comparing BH₃ to AlH₃. Computational calculations have determined the LUMO of borane to be higher in energy than that of AlH₃, which in theory seems odd as the energy of orbitals is expected to increase down a group and therefore the empty 3p of aluminium should have, in theory, occurred higher in energy than the empty 2p orbital of boron. The reason for this may be due to electronic effects but further calculations are required for an exact reason. When also considering orbital overlap and the stabilisation energy of the MO there are four other factors to be considered: orbital size, diffusivity, relative location and orientation. As orbital size increases orbital overlap decreases. The more dense an orbital is the stronger the overlap. The closer orbitals are, the larger their overlap. The more directed an interaction is the better the overlap.

Upon integrating these ideas the BDE of the lewis adduct molecules can be explained. NH₃BH₃ has the strongest dative bond because borane is the strongest lewis acid and although ammonia is a weaker lone pair donor its orbitals are dense, which result in good orbital overlap. Moreover the energy gap between the HOMO and LUMO is small leading to a large splitting energy that stabilises the bonding orbital. The fact that the overlapping orbitals are in relatively close proximity due to the smaller size of the atoms strengthens the bond. This allows good orbital overlap, which results in even more stabilisation of the bonding MO. The difference in bond strength between NH₃AlH₃ and PH₃BH₃ can be accounted by the difference in energy of the HOMO-LUMO gap. The phosphine donor results in the largest energy gaps and therefore suffers a lower amount of stabilisation energy even though it is a stronger donor than ammonia. NH₃AlH₃ has the second strongest dative bond because it has the lowest energy HOMO-LUMO gap but suffers from a greater difference in orbital size than in NH₃BH₃ and so the small amount of extra stabilisation energy it gets from having the lowest HOMO-LUMO gap is hindered by a poor orbital overlap, which counter acts the stabilisation energy causing the dative bond to be weaker than that in NH₃BH₃ but only by +3.3 kJ/mol. The PH₃AlH₃ has the weakest dative bond of all the lewis adduct molecules tested. From looking at the HOMO-LUMO gap it could have been predicted that this molecule would have had the third strongest bond but the stabilisation energy depends on more features than just the difference in energy of the HOMO and LUMO. In this molecule because both phosphorus and aluminium have large orbitals which are diffuse and the relative locations of the orbitals are far apart the stabilisation energy is reduced and the stabilisation of PH₃BH₃ is greater due to better overlap. The resulting poor orbital overlap leads to a weaker bond being formed as the resulting MO is stabilised less than that of the other species.

Further Research

Use of computational chemistry to continue research in this area could be continued by the following. The effect of changing the atoms attached to the donor or acceptor could be calculated as this will affect the lewis acidity or basicity of the species. For example a comparison could be drawn between the BDE of ammonia donating to BF₃, BCl₃, BBr₃ and BI₃, which would show the possible effects of pi-conjugation on the lewis acidity of boron. Alternatively the substituents on the donor atom could be changed for electron withdrawing or donating groups, which would cause the ability of the lone pair donation to change causing an alteration in bond strength. Not only could the substituents be changed for the previous purpose but also for steric effects. Increasing the steric size of the substituents will cause steric repulsion as the species increase their co-ordination number and this should be expected to show a weaker dative bond as steric size increases. Finally other donor or acceptor atoms could be examined so as to increase an understanding of the effects explored within the series of molecules already chosen and to explore effects of hard soft acid bases on the dative covalent bond strength.

References

↑ ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "dative bond".
↑ Ch. Elschenbroich, A. Salzer, Organometallics A concise introduction, sec. edition, 1992

[one-1] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "dative bond".

[two-2] Ch. Elschenbroich, A. Salzer, Organometallics A concise introduction, sec. edition, 1992

[1]

[2]

Bond Dissociation Energies

Optimisation and Frequency Analysis

BH3

AlH3

NH3

PH3

NH3BH3

NH3AlH3

PH3BH3

PH3AlH3