Rep:Mod:nl411 1C

Conformational Analysis using Molecular Mechanics

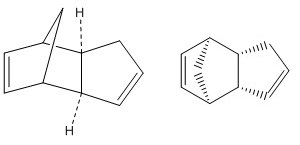
Hydrogenation of Cyclopentadiene Dimer

Molecular mechanics allows the geometry and regioselectivity of the hydrogenation of cyclopentadiene dimer to be predicted. The results obtained can then be used to determine whether kinetic or thermodynamic factors control the reaction. Both dimers 1 and 2 were modelled with their geometries optimised using MMFF94(s) force field. The major applications of cyclopentadiene dimer are resins, petrochemicals and drugs.

Figure 1. 1D and 2D structures of optimised exo dimer 1

Figure 2. 1D and 2D structures of optimised endo dimer 2

Energy Contributions (kcal/mol)

Energy Breakdown	3D structure exo dimer 1	3D structure endo dimer 2
Bond Stretching	3.54999	3.46461
Angle Bending	30.78926	33.29057
Stretching Bending	-2.04241	-2.08480
Torsional	-2.73412	-2.96379
Out-of-Plane Bending	0.01012	0.01585
Van Der Waals	12.79138	12.28893
Electrostatic	13.01103	14.18111
TOTAL	55.37525	58.19247

The enthalpy of dimerisation of cyclopentadiene is 18.0 kcal/mol and yields two stereoisomers (exo and endo products). However, cyclopentadiene dimerises to give endo dimer 2 as the major product as it is kinetically more stable and is therefore formed at a much faster rate. This is an example of when kinetics triumphs over thermodynamics because from the thermodynamic point of view, exo dimer 1, which is the thermodynamic product, should be the dominant product as it is lower in energy (58.19247 of endo dimer vs. 55.37525 kcal/mol of exo dimer).

Exo dimer 1 is lower in energy because it is the less hindered compound i.e. less steric strain. However the observed cyclodimerisation and hydrogenation to give dihydro derivatives 3 and 4 instead result from the endo dimer due to kinetic factors. The stability of endo dimer 2 is explained by the favourable orbital overlap in the transition state. The [4+2] Diels-Alder cycloaddition reaction via exo dimer 1 is under thermodynamic control whereas the reaction via endo dimer 2 is under kinetic control.

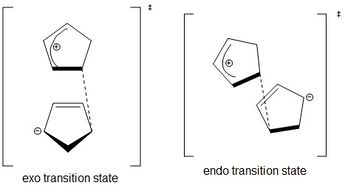
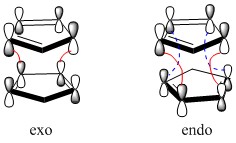
The two cyclopentadienes can come towards each other to react in two different orientations. The group on the dienophile can point away from the diene to give the exo product or towards the diene to give the endo product. In the cycloaddition of two cyclopentadienes, the endo transition state is more favoured due to favourable overlap of p-orbitals on both rings and stabilisation of the structure by the two charges in the resonance form. Figure 3 shows one of the resonance forms of each transition state. Figure 4 shows the orbital interactions in each transition state. In the orbital diagram, the red line refers to the primary interaction, whereas the dashed blue line, which is present only in the endo transition state refers to the secondary interaction. This makes the endo transition state more favoured.

Figure 3. Transition states in the cycloaddition of two cyclopentadienes

Figure 4. Orbital diagrams for the transition states in the cycloaddition of two cyclopentadienes

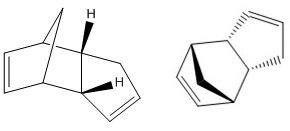
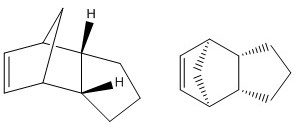
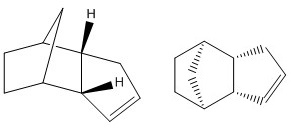
Dihydro derivative 4 has less contributions from the bond stretching energy, angle bending energy, out-of-plane bending energy and Van Der Waals energy than dihydro derivative 3, whereas it has more contributions from stretching bending energy and torsional energy. Electrostatic energies for both dihydro derivatives 3 and 4 are very similar.

Hydrogenation under catalytic conditions of the endo dimer initially gives dihydro derivative 4 as a product. This was rationalised by modelling both dihydro derivatives 3 and 4 with their geometries optimised using MMFF94(s) force field. As a result, dihydro derivative 4 has a lower total energy of 38.31626 kcal/mol (c.f. 48.67900 kcal/mol for dihydro derivative 3) and is therefore, thermodynamically more stable.

The heats of hydrogenation can be used to reveal the relative stabilities of the two dimers. Because the energy of dihydro derivative 4 is lower than the energy of its starting reactant (endo dimer 2), it can be said that the hydrogenation reaction is exothermic. Hydrogenation of cyclopentadiene dimer occurs in two steps. The first step involves hydrogenation of the double bond in the norbornene ring, followed by hydrogenation of the double bond in the five-membered ring of the molecule. This is because the hydrogenation of the norbornene ring double bond occurs at a much faster rate. Both first and second steps release heat with the enthalpies of reaction of 33.2 kcal/mol and 26.2 kcal/mol respectively, and therefore, are both exothermic.

Figure 5. 1D and 2D structures of optimised dihydro derivative 3

Figure 6. 1D and 2D structures of optimised dihydro derivative 4

Energy Contributions (kcal/mol)

Energy Breakdown	3D structure dihydro derivative 3	3D structure dihydro derivative 4
Bond Stretching	3.35176	2.93694
Angle Bending	29.01474	21.05279
Stretching Bending	-2.08247	-1.71435
Torsional	-0.2208	0.15962
Out-of-Plane Bending	0.01262	0.00050
Van Der Waals	13.48941	10.73255
Electrostatic	5.1130	5.14822
TOTAL	48.67900	38.31626

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Taxol is a drug used to treat ovarian cancers. It can exist in two distinct isomeric forms as a result of atropisomerism. Atropisomers are the result of restricted rotation about single bonds. The rings present in intermediates 9 and 10 give rise to the conformational lock; making them atropisomers. Both intermediates were modelled and optimised using MMFF94(s) force field in order to rationalise the relative stabilities.

Figure 7. Intermediates 9 and 10

Energies of Isomers

Isomer #	3D Structure	Energy (kcal/mol)	Notes
9	cyclohexane ring in chair form	70.53232	Comparing to isomer 10 in chair form (with carbonyl pointing down), the structure (carbonyl pointing up) is higher in energy due to steric clash between the oxygen on the carbonyl and the cis-hydrogens.
9	cyclohexane ring in twist-boat form	76.35475	Comparing to isomer 9 in chair form: ca. 6 kcal/mol higher in energy, hence, in good agreement with the literature (ref). Comparing to isomer 10 in twist-boat form: slightly lower in energy
10	cyclohexane ring in chair form	60.5534	Comparing to isomer 9 in chair form: the cis-hydrogens are pointing in opposite direction to the oxygen on the carbonyl, resulting in less steric clash and a lower energy structure Comparing to isomer 10 in twist-boat form: much lower in energy as speculated
10	cyclohexane ring in twist-boat form	77.84221	Comparing to isomer 9 in twist-boat form: slightly higher in energy Comparing to isomer 10 in chairform: much higher in energy, does not agree with literature value

The main conformations of the cyclohexane ring include the chair, half-chair, boat and twist-boat forms. Here, we compare the chair and the twist-boat forms as they are the only two forms which can exist in pure states. Our hypothesis is that the molecule will try to adopt into the chair conformation as it is the most stable form with both torsional and angle strain minimised. In a cyclohexane ring, all carbons are sp³ hybridised and hence the bond angles should theoretically be 109.5°. However, this is not possible if the ring is planar as the bond angles will become 120°; resulting in overall destabilisation of the ring due to torsional strain. Therefore, by adopting a chair conformation, four carbon atoms (C2, C3, C5 and C6) would be in the same plane, one carbon atom would be above the plane and the last one below the plane. This generates the bond angles of 110.9°, which are much closer to the ideal values.

Chair vs Twist-Boat Theoretically, it has been reported that a cyclohexane in a twist-boat form is about 5-6 kcal/mol higher in energy than in a chair form due to more angle strain. However, the two conformations are very similar in energy due to the fact that they have similar shapes with both having no dipole moment.

Results From the assumption that the rest of the molecule is the same for both isomers and that the hydrogens on the carbons interconnecting the two rings in both isomers are cis, intermediate 10, with the carbonyl group pointing down, is thermodynamically more stable than intermediate 9 (carbonyl group pointing up) in both chair and twist-boat forms. Therefore, our hypothesis is correct because the intermediates are also more stable when the cyclohexane ring is in the chair form, rather than in the twist-boat form.

Hyperstable Olefins The stability of the bridgehead alkene in this ten-membered ring was examined by computational modelling. Alkenes positioned at the bridgehead are believed to be unstable and very reactive. However, this is not the case when the size of the ring is very large because most of the ring strain is relieved, whereas in small ring systems, the double bond encounters higher torsional strain. Because the alkene in intermediate 10 is relatively unreactive, it is regarded as a hyperstable olefin. Hyperstable olefins can be defined as alkenes which have less strain than the corresponding or parent alkanes and have negative olefin strain values. Once the ring in which the alkene is contained has reached a certain size, the bridgehead alkene can be considered as a regular acyclic alkene. The stability of hyperstable olefins are attributed to the extra stability provided by the cage structure and not because of steric factors or the energy of the p-bond. Until now, only a small number of hyperstable olefins have been documented.

Spectroscopic Simulation using Quantum Mechanics

Spectroscopy of an Intermediate related to the Synthesis of Taxol

The compounds 17 and 18 are derivatives of isomers 9 and 10. Computer modelling and simulation allows the optimised geometries of these compounds and their 1H and 13 NMR spectra to be predicted. Their spectroscopic information which have been formerly documented are compared to the chemical shifts predicted from the simulation.

In comparing the relative energies of the two isomeric intermediates, a vibrational analysis was also carried out, allowing an entropy and zero-point-energy correction to be computed. These are then used to find the Gibbs free energy ΔG.

Relative Energies of Intermediates 17 and 18 (kcal/mol)

	Intermediate 17	Intermediate 18	Energy Difference
Optimised Geometry Energy	106.265	100.464	5.80
Gibbs free energy ΔG	-1036303.994564	-1036309.648426	5.65

From calculation, intermediate 18 is ca. 5.80 kcal/mol lower in energy than intermediate 17 and is ca. 5.65 kcal/mol higher in Gibbs free energy. This means that intermediate 18 is the more favoured isomeric form. The difference in Gibbs free energy of 23.64 J/mol gives the equilibrium constant K of 0.991, which means that isomerisation from 17 to 18 is favoured. This is in agreement with the calculated optimised geometry energies of both intermediates as intermediate 18 is lower in energy, hence, is more stable.

1H (CDCl₃) NMR Chemical Shifts of Intermediate 18

Literature values (ppm)	Computed values (ppm)	Multiplicity	Good match?	Chemical shifts due to
5.21	6.00	m, 1H	No	H on alkene functional group
3.00-2.70	3.00-2.61	m, 6H	Yes
2.70-2.35	2.55-2.34	m, 3H	Moderate
2.20-1.70	2.28-1.65	m, 6H	Moderate
1.58	1.58	t, 1H	Yes	H on carbon next to carbonyl
1.50-1.20	1.52-1.36	m, 3H	No

Figure 8. 1H NMR of compound 18

13C (CDCl₃) NMR Chemical Shifts of Intermediate 18

Literature values (ppm)	Computed values (ppm)	Good match?	Chemical shifts due to
211.49	213.05	Yes	carbonyl carbon
148.72	148.01	Yes	alkenyl carbon (part of 5-membered ring)
120.9	120.23	Yes	alkenyl carbon (part of the bigger ring)
60.53	65.93	No
51.3	49.67	OK
50.94	48.12	OK
45.53	45.80	Yes	carbon in 5-membered ring containing two sulphur atoms
43.28	44.15	OK	carbon in 5-membered ring containing two sulphur atoms
40.82	41.34	Yes
38.73	38.73	Yes
36.78	33.73	OK
35.45	32.58	OK
30.84	28.42	OK
30.00	26.51	OK
25.56	24.58	Yes
25.35	24.17	Yes
22.21	22.59	Yes

Figure 9. 13C NMR of compound 18

By using the Avogadro software, the geometries of intermediates 17 and 18 were first optimised using MMFF94(s) mechanics force field. Their 1H and 13C NMR spectra were then simulated with chloroform as the solvent. In literature, the NMR spectra were recorded with benzene as a solvent; therefore, differences between the reported values and the calculated values could be partly due to the solvent effects. The chemical shifts for different types of protons change with the solvents. However, the differences for 1H NMR are still minor; allowing comparisons between the literature and calculated chemical shift values to be made with ease, whereas in 13C NMR, the differences in chemical shifts are rather large when different solvents are used.

13C NMR In comparing the reported and calculated chemical shifts, some values are very closely matched; however, the rest which do not match very well could be due to the solvent effects. Also, most of the chemical shifts were not specifically assigned in the literature since it is rather a difficult thing to do as all 13C NMR peaks are singlets and neither the intensity of the peak nor the multiplicity can be used to help in assigning the peak. This has made comparisons even more difficult. There are also anomalous literature chemical shifts (74.61, 21.39 and 19.83 ppm) and anomalous predicted chemical shifts (93.26, 55.03 and 55.03 ppm) which could be due to the heavy sulphur atom. The chemical shifts of carbons attached to heavy atoms are subjected to spin-orbit coupling errors and hence, require a correction. Due to the systematic error present in esters and amides (5 ppm out), any chemical shifts more than 5 ppm away from each other are considered anomalies and cannot be compared.

1H NMR Only chemical shifts of hydrogens on or near the functional groups could be precisely distinguished and specified due to very distinct chemical shift values. However, in general, the results did not show a very good match between the literature and calculated values. In fact, some values were rather anomalous. The protons near the electronegative sulphur atom have signals shifted downfield due to the deshielding effect of electronegative substituents.

Lastly, since the literature values were recorded over two decades ago, the facilities regarding NMR spectroscopy might not be as competent, giving inaccurate results. Therefore, computer simulations may provide more accurate spectroscopic data as necessary corrections can be made such as the dispersion attraction energy.

Analysis of the Properties of the Synthesised Alkene Epoxides

Crystal structures of the two catalysts

Epoxidation by the asymmetric catalysts Shi and Jacobsen produce chiral alkene epoxides. Here we investigate their configurations and rationalise their formation by examining the structures of the two catalysts, the NMR spectra of the resulting epoxides, their absolute configurations and interactions. This was done by modelling the epoxides of trans-stilbene and 1,2-dihydronaphthalene using ConQuest and Mercury.

Shi Catalyst

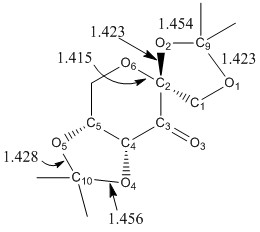
The crystal structures of the pre-catalysts were searched in the Cambridge crystal database (CCDC) using the ConQuest software. The C-O bond lengths for anomeric centres, which were obtained from the Mercury software, are summarised in the following table. Note that a typical C-O single bond length is 1.43 Å and a typical C=O double bond length is 1.24 Å.

C-O Bond Lengths

Bond	Length (Å)	Part of anomeric centre?	Notes
O1-C1	1.429	No	typical C-O bond length
O1-C9	1.423	Yes	shorter than normal C-O bond, anomeric effect
O2-C2	1.423	Yes	shorter than normal C-O bond
O2-C9	1.454	Yes	longer than normal C-O bond, anomeric effect
O3-C3	1.207	No	shorter than normal C=O bond
O4-C4	1.415	No	shorter than normal C-O bond
O4-C10	1.456	Yes	longer than normal C-O bond, anomeric effect
O5-C5	1.437	No	slightly longer than normal C-O bond
O5-C10	1.428	Yes	slightly shorter than normal C-O bond length, anomeric effect
O6-C2	1.415	Yes	shorter than normal C-O bond, part of six-membered ring

The O6-C2 bond length is 0.008 Å shorter than O2-C2 bond and is also the shortest C-O bond for the two anomeric centres present in the molecule. This is because this bond is part of the six-membered ring, which is very stable when in the chair conformation. Conversely, the O2-C9 and O4-C10 bonds are longer than the O1-C9 and O5-C10 bonds respectively due to the same reason; the anomeric effect.

Normally, due to unfavourable steric interactions at the axial position, substituents in a cyclohexane ring would prefer to be in the equatorial position. However, when the anomeric effect is present, electronegative substituents are more notably observed at the axial position. The anomeric effect is when the electronegative substituent at the anomeric position in a cyclohexane ring (i.e. tetrahydropyran) prefers to be in the axial position over the equatorial position. This is due to favourable steric and stereoelectronic interactions i.e. the electron density is donated from the antiperiplanar oxygen lone pair p-orbital (O5-C10) to the antibonding orbital of the C10-O4 bond. This provides an overall stabilising effect, which ultimately increases the bond order of O5-C10 bond (reducing the bond length) and decreases the bond order of C10-O4 bond (increasing the bond length). This effect only takes place when the molecule is the axial conformer as the oxygen lone pair orbital and the C-O bond are antiperiplanar in this conformation. Therefore, we can see that the O2-C9 and O4-C10 bonds are longer than the O1-C9 and O5-C10 bonds respectively. Other C-O bonds which have a length close to the typical C-O bond length are not in the correct orientation to allow the anomeric effect to occur and hence, are not affected by this effect.

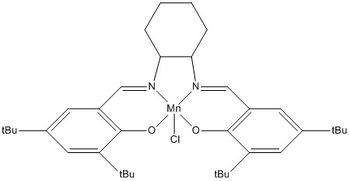
Jacobsen Catalyst

The close approach of the two adjacent t-butyl groups on the rings are discussed in this section. The t-butyl groups determine the trajectory of the incoming alkene. The "side on approach" mechanism gives rise to the p-face selectivity as the incoming cis-alkene attacks the oxo-Mn opposite to the bulky t-butyl groups. This allows a more favourable overlap between the orbitals.

The structure of the Jacobsen catalyst is near planar (the two aromatic rings has a dihedral angle of 169.0(3)° with the chlorine and t-butyl groups pointing out of the plane. The alkene does not approach at the face with the bulky t-butyl group due to steric hindrance, however, the steric effect (steric clash with the axial hydrogens) of the cyclohexane ring is less pronounced. That being said, the fact that the two carbons of the cyclohexane ring are connected in the equatorial manner to the nitrogen, is partly responsible for the ratio of the enantiomers formed. Therefore, the incoming alkene attacks over the diamine bridge, where there is no steric clash with the t-butyl groups and the orbital overlap is more favourable.

Figure 10. Epoxidation products of 1,2-dihydronaphthalene

Figure 11. Epoxidation products of trans-stilbene

Calculated NMR properties of synthesised epoxides

The resulting four epoxides from trans-stilbene and 1,2-dihydronaphthalene were modelled and optimised using Avogadro in order to compute their 1H and 13C NMR spectra. The results are then compared to the literature. Furthermore, from the results, (1S,2R)-1,2-dihydronaphthalene oxide 2 has the same 1H and 13C chemical shifts as (1R,2S)-1,2-dihydronaphthalene oxide 2.

Trans-stilbene oxides

Figure 12. 1H NMR of (S,S)-trans-stilbene oxide (1)

Figure 13. 13C NMR of (S,S)-trans-stilbene oxide (1)

Figure 14. 1H NMR of trans-stilbene oxide (2)

Figure 15. 13C NMR of trans-stilbene oxide (2)

Figure 16. 1H NMR of 1,2-dihydronaphthalene oxide (1)

Figure 17. 13C NMR of 1,2-dihydronaphthalene oxide (1)

Figure 18. 1H NMR of 1,2-dihydronaphthalene oxide (2)

Figure 19. 13C NMR of 1,2-dihydronaphthalene oxide (2)

1H (CDCl₃) NMR Chemical Shifts of (S,S)-trans-stilbene oxide 1

Literature values (ppm)	Computed values (ppm)	Integration	Chemical shifts due to
7.11-7.0	7.50(2), 7.40(2), 7.33(4), 7.25(2)	10H	aromatic H
4.24	4.30	2H	H on carbon next to O

13C (CDCl₃) NMR Chemical Shifts of (S,S)-trans-stilbene oxide 1

Literature values (ppm)	Computed values (ppm)	Integration	Chemical shifts due to
134.8	131.28	2C	C on aromatic ring connecting to epoxide C
128.7, 127.6, 127.3	122.90, 122.62, 122.32, 122.12	10C	aromatic carbon
60.2	62.02	2C	carbon adjacent to O

1H (CDCl₃) NMR Chemical Shifts of trans-stilbene oxide 2

Literature values (ppm)	Computed values (ppm)	Integration	Chemical shifts due to
7.57-7.34	7.57-7.48	10H	aromatic H
3.91	3.54	2H	H on carbon next to O

(ref11)

13C (CDCl₃) NMR Chemical Shifts of trans-stilbene oxide 2

Literature values (ppm)	Computed values (ppm)	Integration	Chemical shifts due to
137.6	134.09	2C	C on aromatic ring connecting to epoxide C
129.0, 128.8, 126.2	124.22, 123.51, 123.21, 123.07, 118.27	10C	aromatic carbon
63.3	66.43	2C	carbon adjacent to O

1,2-dihydronaphthalene oxides

1H (CDCl₃) NMR Chemical Shifts of (1R,2S)-1,2-dihydronaphthalene oxide 1

Literature values (ppm)	Computed values (ppm)	Integration, multiplicity
7.44	7.49	1H, d
7.33-7.21	7.39	2H, m
7.13	7.20	1H, d
3.89	3.59	1H, d
3.77	3.59	1H, t
2.83-2.79	2.88	1H, m
2.59-2.55	2.27	1H, m
2.49-2.41	2.22	1H, m
1.80-1.76	1.56	1H, m

13C (CDCl₃) NMR Chemical Shifts of (1R,2S)-1,2-dihydronaphthalene oxide 1

Literature values (ppm)	Computed values (ppm)	Integration
137.1	133.84	1C
132.9	130.38	1C
129.9	125.55	1C
129.8	123.84	1C
128.8	123.43	1C
126.5	121.44	1C
55.5	56.43	1C
53.2	54.83	1C
24.8	28.04	1C
22.2	24.95	1C

Assigning absolute configuration of synthesised epoxides (optical rotations)

The chiropical properties of the four epoxides were calculated and compared to available literature values. This helps to predict the enantioselectivity of the catalyst. Here we investigate the optical rotation (i.e. the optical rotatory power) at the specified wavelengths of 365 nm and 589 nm. However, most epoxides do not have their optical rotation documented in literature and hence, comparisons cannot be made.

Predicting the optical rotation using computer modelling should give more accurate results even though at very low values, results can be unreliable.

Optical Rotation of Epoxides at Wavelength 365 nm

Epoxide	Lit. optical rotation (deg)	Calculated optical rotation (deg)
trans-stilbene oxide S,S	-	1254.12
cis-stilbene oxide	-	-0.54
1,2-dihydronaphthalene oxide S,R	-133	-523.05
1,2-dihydronaphthalene oxide R,S	+133	-210.15

Optical Rotation of Epoxides at Wavelength 589 nm

Epoxide	Lit. optical rotation (deg)	Calculated optical rotation (deg)
trans-stilbene oxide S,S	-	0.20
cis-stilbene oxide	-	297.54
1,2-dihydronaphthalene oxide S,R	-	-156.73
1,2-dihydronaphthalene oxide R,S	-	-36.01

Calculated properties of the reaction transition state of stilbene and dihydronaphthalene

The pre-computed free energies of all possible transition states for the epoxidation of trans-stilbene and 1,2-dihydronaphthalene are shown in the tables. In each case, the free energy difference between the lowest energy transition states of the two possible configurations was used to calculate the equilibrium constant (K) and the enantiomeric excess (ee). The was was then compared to the literature value as a check. Furthermore, the calculated optical rotations were also compared to the literature-reported values. The equilibrium constant (K) and the % enantiomeric excess (ee) can be calculated using the equations shown below.

Transition States for Shi Epoxidation of Trans-stilbene

Absolute config.	Gibbs Free Energy ΔG (J/mol)
R,R (1)	-4044727729
R,R (2)	-4044726264
R,R (3)**	-4044759959
R,R (4)	-4044759601
S,S (1)	-4044716217
S,S (2)	-4044720563
S,S (3)	-4044743569
S,S (4)*	-4044738403

Transition States for Shi Epoxidation of 1,2-Dihydronaphthalene

Absolute config.	Gibbs Free Energy ΔG (J/mol)
R,S (1)	-3639996027
R,S (2)	-3640009479
R,S (3)*	3640031019
R,S (4)	-3640011682
S,R (1)	-3640023861
S,R (2)	-3639983711
S,R (3)	-3640009882
S,R (4)**	-3640036765

Transition States for Jacobsen Epoxidation of Trans-stilbene

Absolute config.	Gibbs Free Energy ΔG (J/mol)
S,S**	-9421844928
R,R	-9421839886

Transition States for Jacobsen Epoxidation of 1,2-Dihydronaphthalene

Absolute config.	Gibbs Free Energy ΔG (J/mol)
S,R (1)**	-9017147414
S,R (2)	-9017127772
R,S (1)	-9017121905
R,S (2)*	-9017122287

Shi epoxidation of tran-stilbene The free energy difference between the lowest energy transition states R,R (3) and S,S (4) is 21556.06367 J/mol, which gives the equilibrium constant K of 0.000167236 and the enantiomeric excess of the epoxide R,R (3) to be 99.9%. This is very similar to the literature-reported value of 98.3%.

Shi epoxidation of 1,2-dihydronaphthalene The free energy difference between the lowest energy transition states R,S (3) and S,R (4) is 5745.472404 J/mol, which gives the equilibrium constant K of 0.098487423 and the enantiomeric excess of the epoxide S,R (4) to be 82.06853876%. This is much higher than the literature value of 68%.

Jacobsen epoxidation of trans-stilbene The free energy difference between the lowest energy transition states S,S and R,R is 5041.783813 J/mol, which gives the equilibrium constant K of 0.130818312 and the enantiomeric excess of the epoxide S,S to be 76.86307147%. This is higher than the literature value of 67%.

Jacobsen epoxidation of 1,2-dihydronaphthalene The free energy difference between the lowest energy transition states S,R (1) and R,S (2) is 25127.21739 J/mol, which gives the equilibrium constant K of 3.95965E-05 and the enantiomeric excess of the epoxide S,R (1) to be 100%. This is much higher than the literature value of 78%.

Non-covalent interactions in the active-site of the reaction transition state

Figure 20. NCI interactions of the transition state

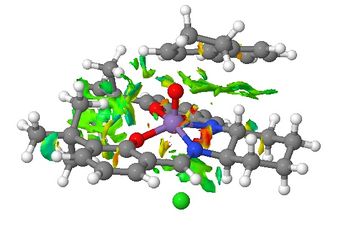
In order to examine the non-covalent interactions (NCI) in the transition state of the Jacobsen epoxidation of 1,2-dihydronaphthalene, the electron density of the system was computed on Gaussview and then subjected to an NCI analysis. NCIs include hydrogen-bonding, electrostatic attractions and dispersion forces. The results (shown in Figure 20) are indicated by the coloured regions with reduced density-gradient, where different colours indicate various interaction strengths. Blue means the interaction is strongly attractive, green is weakly attractive, yellow is weakly repulsive and red is strongly repulsive.

We can see that there are very few ‘red’ and 'yellow' interactions, meaning that the substrate tries to align itself in a way that repulsion with the catalyst is minimised. However, there is no region of the blue colour as NCIs are based on weak non-covalent interactions, which are less dependent on distance and direction. The region where there is a mixture of colours is where the bond is forming in the transition state (considered as “half covalent”) and is normally neglected. This type of diagram may help to reveal the regions in which the substrate and the catalyst interact and therefore, may be used to rationalise the stereoselectivity.

From our result, multiple NCIs (green regions) are observed between the catalyst and the alkene, indicating mildly attractive NCI interaction between the substrate and the catalyst. This means that the transition state is stabilised by many attractive forces. There are also green regions between the benzene rings of the catalyst and the alkene. These interactions are favourable as they are similar to the pi stacking of aromatic rings.

Electronic topology (QTAIM) in the active-site of the reaction transition state

Figure 21. Electronic topology for Jacobsen epoxidation of 1,2-dihydronaphthalene R,S (2)

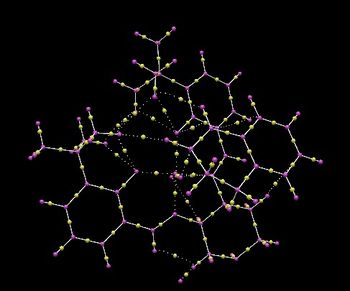
The QTAIM analysis focuses on both the electron density in the covalent interactions and in the non-covalent regions as mentioned previously. A bond critical point is defined as the region along the bond path where the first derivative of the electron density is at the minimum. Other types of critical point associated with nuclei, rings and cages are neglected here. The transition state of the Jacobsen epoxidation of 1,2-dihydronaphthalene was modelled using Avogadro2. In the QTAIM analysis, the bond critical points are indicated by the yellow spheres connecting the two nuclei. The yellow sphere in the middle of the dashed line indicates weak interaction between oxygen and hydrogen, which is a non-covalent bond critical point. The limitations of the software mean that accurate coordinates of the bond critical points cannot be defined and only qualitative estimation of their positions can be made.

The bond between the carbon atom and the electronegative heteroatoms O and N has a higher electron density shifted towards the electronegative atom and a minimum electron density at the carbon atom. Conversely, as the electron density is equally shared between the two carbon atoms in the benzene ring, the BCP is observed at the centre of the bond. There are also weak non-covalent BCPs between the O atoms of the catalyst and H atoms of the alkene, indicating hydrogen-bonding, which helps to stabilise the overall transition state.

According to the NCI analysis previously carried out, we can see that the Jacobsen catalyst relies on both covalent and non-covalent interactions to interact with the alkenes. The presence of multiple non-covalent interactions allows high stereocontrol to be achieved as these interactions depend less on the distance and direction.

New candidates for investigations

4-isopropenyl-1-methyl-7-oxa-bicyclo[4.1.0]heptane would be an interesting epoxide to investigate because one might expect the cyclohexane ring to adopt the chair conformation as it is the most stable form. However, due to the two R groups attached at the 1 and 4 positions, the conformation which the molecule will try to adopt could be more complicated.

By using various modelling techniques previously encountered in this computational lab, various aspects of this epoxide can be studied including the transition state, strain and energy of different conformers, the repulsion effect between the R groups and the direction in which the oxygen may point to.