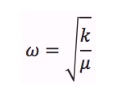Jump to content

Rep:Mod:nl411

From ChemWiki

Accuracy of reported numbers

In this work, numbers are reported in such a way that the convention is followed and as much as possible, to the best of their accuracy. Therefore, energies are reported to 8 decimal places (d.p.) in a.u. and 2 d.p. in kJ/mol. Dipole moments (Debye) are reported to 2 d.p., frequencies (cm-1) and their intensities are reported in integers, bond distances (Å) are reported to 2 d.p., and bond angles (°) are reported to 1 d.p..

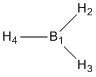
Optimising a BH3 molecule

Quantum chemistry can be used to determine the structure and bonding of a molecule. Here, a molecule of BH3 was optimised using the B3LYP method and the 3-21G basis set.

Results


3-21G BH3 optimisation file link: File:NL BH3 OPT.LOG


Optimised B-H bond distances

B1-H2: 1.19 Å

B1-H3: 1.19 Å

B1-H4: 1.19 Å


Optimised H-B-H bond angles

H4-B1-H2: 120.0°

H4-B1-H3: 120.0°

H3-B1-H2: 120.0°


BH3 optimisation
File Name NL_bh3_opt
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Charge 0
Spin Singlet
E(RB3LYP) -26.46226429 a.u.
RMS Gradient Norm 0.00008851 a.u.
Dipole Moment 0.00 Debye
Point Group CS
Job cpu time 19.0 seconds 


        Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000709     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672478D-07

Therefore, the optimisation is converged.

Optimising a BH3 molecule using a higher level basis set

In this part, a molecule of BH3 was optimised using the B3LYP method and the 6-31G(d,p) basis set.

Results

6-31G(d,p) BH3 optimisation file link: File:NL BH3 OPT 631G DP.LOG

Optimised B-H bond distances

B1-H2: 1.19 Å

B1-H3: 1.19 Å

B1-H4: 1.19 Å


Optimised H-B-H bond angles

H4-B1-H2: 120.0°

H4-B1-H3: 120.0°

H3-B1-H2: 120.0°


BH3 optimisation
File Name NL_BH3_OPT_631g_dp
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -26.61532358 a.u.
RMS Gradient Norm 0.00008206 a.u.
Dipole Moment 0.00 Debye
Point Group CS
Job cpu time 20.0 seconds 


         Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000099     0.000300     YES
 Maximum Displacement     0.000875     0.001800     YES
 RMS     Displacement     0.000418     0.001200     YES
 Predicted change in Energy=-1.452139D-07

Hence, the optimisation is converged.


The 3-21G optimised structure of BH3 has a total energy of -26.46226429 a.u., whilst the 6-31G(d,p) optimised structure has a total energy of -26.61532358 a.u and therefore, the energies of the BH3 molecule calculated from the two basis sets are different by 0.15305929 a.u. (401.86 kJ/mol).

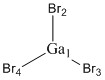
Optimising a GaBr3 molecule using pseudo-potentials and larger basis sets

Here, a molecule of GaBr3 was optimised using the B3LYP method and the LanL2DZ basis set.

Results

LANL2DZ GaBr3 optimisation file link: File:NL GABR3 OPT LANL2DZ.LOG

Optimised Ga-Br bond distances

Ga1-Br2: 2.35 Å

Ga1-Br3: 2.35 Å

Ga1-Br4: 2.35 Å


Optimised Br-Ga-Br bond angles

Br2-Ga1-Br3: 120.0°

Br3-Ga1-Br4: 120.0°

Br2-Ga1-Br4: 120.0°


GaBr3 optimisation
File Name NL_GaBr3_opt_LanL2DZ
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set LANL2DZ
Charge 0
Spin Singlet
E(RB3LYP) -41.70082783 a.u.
RMS Gradient Norm 0.00000016 a.u.
Dipole Moment 0.00 Debye
Point Group D3H
Job cpu time 8.0 seconds 


         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282698D-12

Hence, the optimisation is converged.

The optimised Ga-Br bond length is slightly longer than the literature-reported value (2.35 Å vs. 2.249 Å). However, it is still in good agreement with the literature and therefore, the result is said to be reasonable. [1]

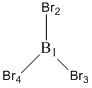
Optimising a BBr3 molecule using a mixture of basis-sets and psuedo-potentials

Because the BBr3 molecule contains both heavy atoms i.e. Br atoms and a light B atom, a combination of a pseudo-potential and a full basis set is needed to optimised the molecule. Therefore, the calculation method and the basis set used in this case were B3LYP and GEN respectively.


Results


GEN BBr3 optimisation file link: File:NL BBR3 OPT GEN.LOG

Optimised B-Br bond distances

B1-Br2: 1.93 Å

B1-Br3: 1.93 Å

B1-Br4: 1.93 Å


Optimised Br-B-Br bond angles

Br2-B1-Br3: 120.0°

Br4-B1-Br3: 120.0°

Br2-B1-Br4: 120.0°


BBr3 optimisation
File Name NL_BBr3_OPT_GEN
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
E(RB3LYP) -64.436450543 a.u.
RMS Gradient Norm 0.00001117 a.u.
Dipole Moment 0.00 Debye
Point Group CS
Job cpu time 24.0 seconds 


         Item               Value     Threshold  Converged?
 Maximum Force            0.000020     0.000450     YES
 RMS     Force            0.000011     0.000300     YES
 Maximum Displacement     0.000077     0.001800     YES
 RMS     Displacement     0.000044     0.001200     YES
 Predicted change in Energy=-1.113676D-09

Comparing structures of BH3, BBr3 and GaBr3

Bond Distance Comparison (Å)
M-X2 M-X3 M-X4 Average
BH3 (1) 1.19 1.19 1.19 1.19
BH3 (2) 1.19 1.19 1.19 1.19
GaBr3 2.35 2.35 2.35 2.35
BBr3 1.93 1.93 1.93 1.93

Note:

1) M = central atom, X2 = first ligand, X3 = second ligand, X4 = third ligand

2) BH3 (1) results are based on the 3-21G basis set, whereas BH3 (2) results are based on the 6-31G(d,p) basis set


The BH3, BBR3 and GaBr3 molecules are all Lewis acidic; meaning that they each have 6 valence electrons. BR3 compounds can exist as monomers due to stabilisation by hyperconjugation. However, BH3 can only exist as an adduct, for instance, BH3.THF and BH3.SMe2.

The average bond distance is the longest for GaBr3 and the shortest for BBr3. The average bond distance for BH3 is in-between the other two molecules. This implies that Ga-Br bond is the weakest as the overlap between the Ga and Br orbitals is relatively small, whereas B-Br bond is the strongest as the overlap between the B and Br orbitals is large. This is because the B and Br atoms are more similar in size.

The ligands referred to here are the atoms bonding to the central atom i.e. H and Br atoms. H is very small, whilst Br is rather big. H also has only 1 valence e-, whereas Br has 7 valence e-Therefore, each needs 1 e- to complete the octet. Therefore, by changing the ligand, the size of the orbital overlap between the central atom and the ligand is changed as the ligands are of different sizes. On the other hand,changing the central atom changes the number of the ligands needed to complete the octet. This is because as the size of the central atom is changed, the number of the ligands that can fit around the central atom changes. The central atoms here at B and Ga. B and Ga are both Group 13 elements and therefore, are both e- poor. However, B is more electronegative than Ga, whilst Ga is larger than B as it is lower down in the periodic table.

From the results, B and H atoms have the best orbital overlap, meaning that the B and H orbitals have good energy and size match, and so the B-H bond is BH3 is the strongest and hence, the shortest. On the contrary, the orbital overlap between the Ga and Br atoms in GaBr3 is rather poor due to a mismatch in size and energy and therefore, the Ga-Br bond length is the weakest and hence, the longest. The overlap between the B and Br atoms in BBr3 is poorer than the overlap between the B and H atoms in BH3, however, the orbital overlap is still better than that in GaBr3. Therefore, the B-Br bond length of BBr3 is in-between the B-H and Ga-Br bond lengths in BH3 and GaBr3 respectively.

Gaussview will not draw the bonds in the structure if the bond distances exceed the pre-defined values. Therefore, it does not mean that there are no bonds. According to IUPAC[2], a chemical bond is believed to exist between two atoms or groups of atoms when there are attractive forces in-between the nuclei of the two atoms (or groups of atom), which gives rise to a region of "constant potential contours". This decreases the overall potential energy substantially, whilst increases the kinetic energy but only to a very small extent. This includes covalent bonds in organic molecules, ionic bonds in ionic salts such as sodium chloride, as well as bonds between aluminium and water molecules in hexaaqua aluminium ion.

BH3 frequency analysis

In order to confirm that the structures of the molecules are the minimum structures i.e. the molecules are fully optimised, a frequency (or vibrational) analysis can be carried out. Thus, a frequency analysis of a BH3 molecule was carried out to determine whether the structure was a minimum.

6-31G(d,p) BBr3 frequency analysis file link: File:NL BH3 ULTRAFINE FREQ.LOG

Real output: 

 Low frequencies ---  -12  -12   -7   0    0    0
 Low frequencies --- 1163 1213 1213
BH3 Vibrational Modes
No. Form of the vibration Description Frequency Intensity Symmetry D3h
1 All H atoms move up and down in the direction of the black arrows in a concerted manner, whilst the B atom is stationary. 1163 93 A2"
2 All H atoms move back and forth in the direction of the black arrows in a concerted manner, whilst the B atom is stationary. 1213 14 E'
3 Only two H atoms to the right of the image move back and forth in the direction of the black arrows in a concerted manner, whilst the remaining H atom and the B atom are stationary. 1213 14 E'
4 All three H atoms move away from the B atom and towards the B atom in a concerted manner (along the direction of the black arrows), whilst the B atom is stationary. 2583 0 A1' totally symmetric
5 Only two H atoms to the right of the image move away from the B atom and towards the B atom alternately, whilst the remaining H atom and the B atom are stationary. 2716 126 E'
6 Two H atoms to the right of the image move away from the B atom and towards the B atom in a concerted manner and at the same time when these two H atoms move away from the B atom, the remaining H atom moves in the opposite direction i.e. towards the B atom, and vice versa. The B atom is stationary. 2716 126 E'


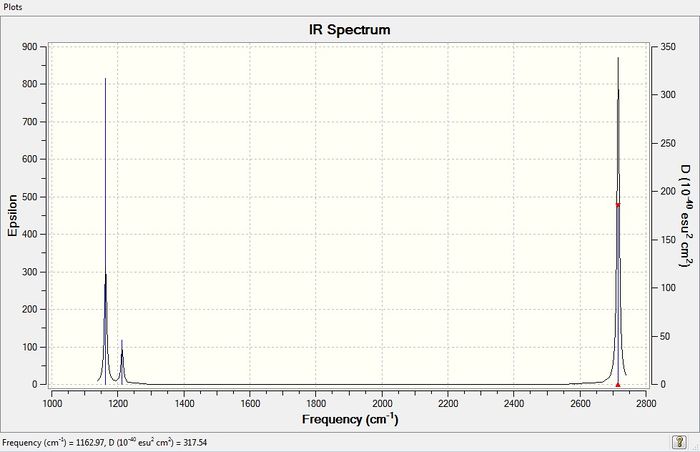
IR Spectrum of BH3

Why are there less than six peaks in the IR spectrum when there are six vibrations?

Only vibrational modes which cause a change in dipole moment give rise to the peaks in the IR spectrum. Since the vibrational mode corresponding to the A1' symmetry does not create a change in dipole moment, it does not contribute to any peak in the IR spectrum. The rest of the vibrational modes give rise to a change in dipole moment, however, there are only three peaks and not five because vibrational modes 2 and 3, and vibrational modes 5 and 6, are two degenerate pairs; giving rise to two IR peaks. Thus, the last IR peak present in the spectrum is attributed to the vibrational mode 1 with the symmetry A2".

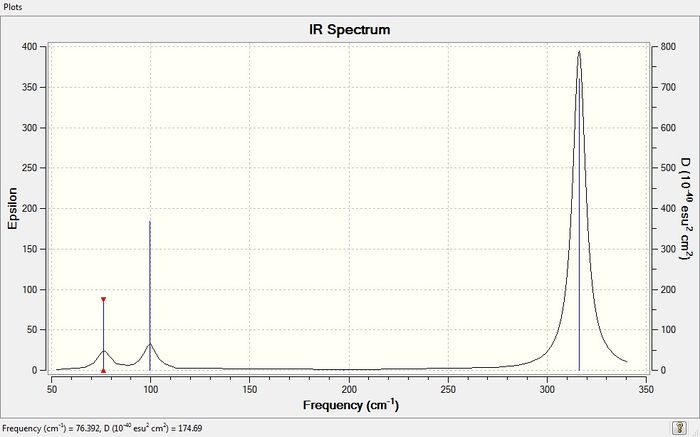
GaBr3 frequency and vibrational analysis

A frequency analysis of GaBr3 was carried out to confirm that the structure was a minimum.

Completed frequency analysis job link: File:NL GABR3 OPT LANL2DZ ULTRAFINE FREQ.LOG

Real output: 

 Low frequencies ---   -1   0   0    0    1    1
 Low frequencies ---   76   76   100
GaBr3 Vibrational Modes
No. Form of the vibration Description Frequency Intensity Symmetry D3h
1 The two Br atoms to the right of the image move away from the Ga atom and towards the Ga atom in a concerted manner and at the same time when these two Br atoms move away from the Ga atom, the central Ga atom moves along the direction of the black arrows as well but in the opposite direction, and vice versa. The remaining Br atom (left of image), which is supposed to be stationary, is effectively moving as well as a result of the central Ga atom it is attached to, moving. 76 3 E'
2 All four atoms are moving in a concerted manner along the indicated direction of the black arrows. 76 3 E'
3 The central Ga atom moves up and down (along the direction of the black arrows) in a more aggressive manner than the three Br atoms which also move up and down in a concerted manner (along the direction of the black arrows) but to a lesser extent. 100 9 A"
4 The three Br atoms move towards the central Ga atom and away from the Ga atom (in the direction of the black arrows) in a concerted manner, whilst the central Ga atom is stationary. 197 0 A'
5 The bottom Br in the image and the central Ga move back and forth towards each other concertedly, whilst to a much lesser extent, the remaining two Br atoms move in a concerted manner back and forth towards the central Ga (in the direction of the black arrows). 316 57 E'
6 The central Ga atom moves left and right as indicated by the black arrows on the atom, whilst the Br atom at the back is stationary and the two remaining Br atoms at the front move back and forth alternately along the direction of the black arrows. 316 57 E'


What is the lowest "real" normal mode?

The lowest "real" normal modes are the vibrational modes numbered 1 and 2. Because they have the same lowest frequency of all the vibrational modes, which is 76 cm-1.


IR Spectrum of GaBr3

Comparing vibrational frequencies of BH3 and GaBr3

Comparing vibrational frequencies of BH3 and GaBr3
BH3 GaBr3
Vibrational mode 1 1163 (93) 76 (3)
Vibrational mode 2 1213 (14) 76 (3)
Vibrational mode 3 1213 (14) 100 (9)
Vibrational mode 4 2583 (0) 197 (0)
Vibrational mode 5 2716 (126) 316 (57)
Vibrational mode 6 2716 (126) 316 (57)

Note: The numbers in brackets are the intensities


Comparing the frequencies of BH3 and GaBr3

As the vibration frequencies of BH3 in general are much higher than the vibration frequencies of GaBr3, this implies that B-H bonds are much stronger than Ga-Br bonds. Moreover, this indicates a higher bond dissociation energy for BH3 than for GaBr3. There has also been a reordering of vibrational modes going from BH3 to GaBr3. For BH3, the two lowest frequencies correspond to the two degenerate levels. However, the lowest vibrational frequency for GaBr3 is not part of the degenerate levels. However, the IR spectra of the two molecules are still very similar as they both have three peaks. This is because both molecules still have two degenerate vibrational levels. For both spectra, the A2 and E' modes lie close in energy, as well as the A1' and E' modes. However, the A1' and E' modes are higher in energy because they correspond to the stretching modes. The higher energy vibrations correspond to the stretching modes of the molecule, whereas the lower energy vibrations correspond to the angle-bending modes of the molecule. It can be seen that for the higher energy vibrations, the atoms vibrate to a much greater extent i.e. "stretch", whilst the atoms only "bend" in and out (vibrate to a much lesser extent) in the low energy vibrations.

In simple harmonic motion, the vibrational frequency depends on the square root of the spring constant k over the reduced mass of the molecule as shown by the equation below. Therefore, the higher the reduced mass of the molecule, the lower the vibrational frequency. This means that the GaBr3 molecule which has a molar mass of 309.4 g/mol, is much heavier than the BH3 molecule, with the molar mass of 13.8 g/mol and thus, the vibrational frequencies of GaBr3 are much lower.

The purpose of a frequency analysis is to ensure that the optimised structure of a molecule is a minimum. Furthermore, it allows experimental data i.e. the real IR spectrum, to be checked by comparing with the calculated data. The same method and basis set must be used for both the optimisation and frequency analysis calculations because frequencies are essentially the second derivative of the potential energy surface i.e. the energy with respect to the position of the nucleus. Therefore, if the optimisation of a molecule is computed using a certain combination of method and basis set on a certain potential energy surface, the frequency analysis should also be done on the same potential energy surface, using the same combination of method and basis set.

The top line of "Low frequencies" represent the centre of mass motions. The six frequencies correspond to three translational modes (i.e. the molecule can move in x, y and z-axis) and three rotational modes. Therefore, as these motions are very weak, all frequencies are very close to zero. The bottom line of "Low frequencies" correspond to the six vibrational modes of the molecule. These vibrational frequencies are much higher than translational and rotational frequencies.

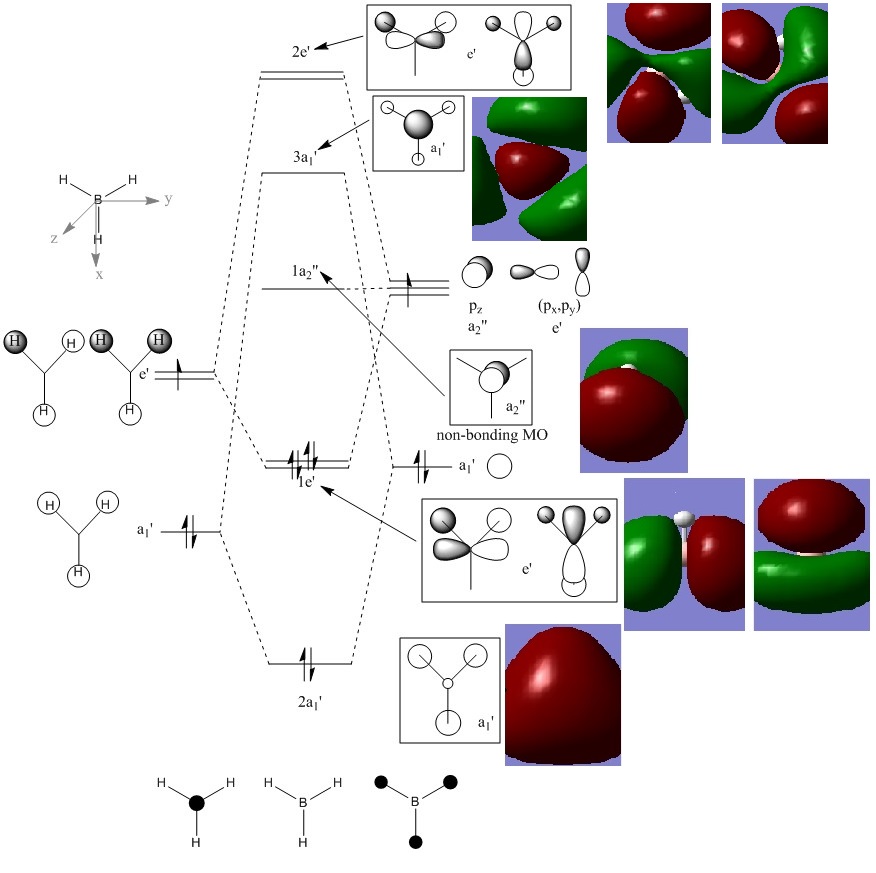
Molecular orbitals of BH3

As the calculations are carried out, the electronic structures of molecules can be solved, producing MOs as a result. This is very useful as these computed MOs can be compared to the MOs generated by MO diagrams, which are rather qualitative. Therefore, a population analysis of a BH3 molecule was carried out in order to obtain the "real" MOs. The population analysis was carried out using the same method and basis set combination as that used in the optimisation step.

Completed population analysis link: File:NL BH3 ULTRAFINE OPT ENERGY.LOG


The differences between the real MOs and the LCAO MOs are rather small. Therefore, this suggests that the MO theory is a very accurate and useful method for qualitatively predicting the bonding, structure and reactivity of molecules. Furthermore, the qualitative method can also be done relatively fast.

NBO Analysis of NH3

A natural bond orbital analysis of NH3 was carried out. However, the Gaussview software only presents a graphical interface of the atomic charges, hence, the information regarding the NBO analysis must be extracted directly from the .log file.


6-31G(d,p) NH3 optimisation file link: File:NL NH3 OPT 631G DP.LOG


Optimised N-H bond distances

N1-H2: 1.02 Å

N1-H3: 1.02 Å

N1-H4: 1.02 Å


Optimised H-N-H bond angles

H2-N1-H4: 105.7°

H3-N1-H4: 105.7°

H3-N1-H2: 105.7°


NH3 optimisation
File Name NL_nh3_opt_631g_dp
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -56.55776873 a.u.
RMS Gradient Norm 0.00000323 a.u.
Dipole Moment 1.85 Debye
Point Group C3V
Job cpu time 10.0 seconds 


         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000015     YES
 RMS     Force            0.000004     0.000010     YES
 Maximum Displacement     0.000012     0.000060     YES
 RMS     Displacement     0.000008     0.000040     YES
 Predicted change in Energy=-9.846667D-11

Hence, the optimisation is converged.


Completed frequency analysis: File:NL NH3 OPT 631G DP FREQ.LOG

Real output: 

Low frequencies ---   0   0   0    7    8    8
Low frequencies --- 1089 1694 1694


6-31G(d,p) NH3 population analysis file link: File:NL NH3 OPT 631G DP POPU.LOG


NH3 charge distribution:

The charge range is -1.125 to +1.125, where -1.125 is the brightest red region and +1.125 is the brightest green region. The bright green colour on all H atoms indicates that each H atom has a highly positive charge, whilst the bright red colour on the N atom indicates that it has a highly negative charge, which is expected of an electronegative atom.

NBO charges for N and H atoms in NH3
N1 -1.125
H2 0.375
H3 0.375
H4 0.375 

******************************Gaussian NBO Version 3.1******************************
             N A T U R A L   A T O M I C   O R B I T A L   A N D
          N A T U R A L   B O N D   O R B I T A L   A N A L Y S I S
 ******************************Gaussian NBO Version 3.1******************************



Summary of Natural Population Analysis:                  
                                                          
                                       Natural Population 
                Natural  -----------------------------------------------
    Atom  No    Charge         Core      Valence    Rydberg      Total
 -----------------------------------------------------------------------
      N    1   -1.12514      1.99982     6.11104    0.01429     8.12514
      H    2    0.37505      0.00000     0.62250    0.00246     0.62495
      H    3    0.37505      0.00000     0.62250    0.00246     0.62495
      H    4    0.37505      0.00000     0.62250    0.00246     0.62495
 =======================================================================
   * Total *    0.00000      1.99982     7.97852    0.02166    10.00000


       (Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.99909) BD ( 1) N   1 - H   2  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.0000
                                            0.0000  0.8155  0.0277 -0.2910  0.0052
                                            0.0000  0.0000 -0.0281 -0.0087  0.0014
                ( 31.17%)   0.5583* H   2 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000  0.0000 -0.0289  0.0072
     2. (1.99909) BD ( 1) N   1 - H   3  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000 -0.7062
                                           -0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                            0.0076  0.0243  0.0140  0.0044  0.0014
                ( 31.17%)   0.5583* H   3 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000  0.0250  0.0145  0.0072
     3. (1.99909) BD ( 1) N   1 - H   4  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.7062
                                            0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                           -0.0076 -0.0243  0.0140  0.0044  0.0014
                ( 31.17%)   0.5583* H   4 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000 -0.0250  0.0145  0.0072
     4. (1.99982) CR ( 1) N   1           s(100.00%)
                                            1.0000 -0.0002  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
     5. (1.99721) LP ( 1) N   1           s( 25.38%)p 2.94( 74.52%)d 0.00(  0.10%)
                                            0.0001  0.5036 -0.0120  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.8618 -0.0505
                                            0.0000  0.0000  0.0000  0.0000 -0.0310


     Threshold for printing:   0.50 kcal/mol
                                                                              E(2)  E(j)-E(i) F(i,j)
         Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u. 


Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (H3N)
     1. BD (   1) N   1 - H   2          1.99909    -0.60417   
     2. BD (   1) N   1 - H   3          1.99909    -0.60417   
     3. BD (   1) N   1 - H   4          1.99909    -0.60417   
     4. CR (   1) N   1                  1.99982   -14.16768   
     5. LP (   1) N   1                  1.99721    -0.31757

Association energies: Ammonia-Borane

Hydrogen is a potential future fuel. Therefore, studies regarding its storage are of great importance and ammonia borane is one of the candidates as a solid matrix to store hydrogen in as it is hydrogen-abundant and is stable at room temperature. Furthermore, ammonia borane is an acid-base complex, meaning that donation of electrons from the N atom to the B atom is anticipated, however, this is not the case. Therefore, the association and conversely, the dissociation energy of an NH3BH3 molecule was calculated using the energy of the reactants i.e. NH3 and BH3, and energy of the products i.e. NH3BH3 of the reaction. The energy of the reactants and products were computed using the same method and basis set, which were B3LYP and 6-31G(d,p) respectively.

NH3BH3 6-31G(d,p) optimisation file link: File:NL NH3BH3 OPT 631G DP.LOG

Optimised N-H bond distances

N7-H1: 1.12 Å

N7-H2: 1.12 Å

N7-H3: 1.12 Å

Optimised B-H bond distances

B8-H4: 1.12 Å

B8-H5: 1.12 Å

B8-H6: 1.12 Å


Optimised H-N-H bond angles

H1-N7-H2: 108.2°

H2-N7-H3: 108.2°

H1-N7-H3: 108.2°

Optimised H-B-H bond angles

H4-B1-H2: 108.2°

H4-B1-H3: 108.2°

H3-B1-H2: 108.2°

NH3BH3 optimisation
File Name nl_nh3bh3_opt_631g_dp
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -83.22468908 a.u.
RMS Gradient Norm 0.00000138 a.u.
Dipole Moment 5.56 Debye
Point Group C1
Job cpu time 1 minute 21.0 seconds 


         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000034     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-1.180736D-10


NH3BH3 completed frequency analysis file link File:NL NH3BH3 OPT 631G DP FREQ2.LOG 

Low frequencies ---   -5   -2    0    0    0    3
Low frequencies ---  263  633  638


E(NH3) = -56.55776873 a.u. E(BH3) = -26.61532358 a.u. E(NH3BH3) = -83.22468908 a.u.

Energy difference = E(NH3BH3) - [E(NH3)+E(BH3)] = -0.05159677 a.u. (-135.47 kJ/mol).

Converting -0.05159677 a.u. to kJ/mol, the NH3BH3 association energy and hence, dissociation energy, is -135.47 kJ/mol.

Ammonia borane is a Lewis acid-base adduct[3] and thus, the N-B bond is a dative covalent bond with the electrons being shared between the N and B atoms. A diatomic N-B molecule has a bond dissociation energy of 377.9 kJ/mol.[1] Therefore, because the N-B bond in ammonia borane is not a pure covalent bond, the molecule's dissociation energy should be lower than that in the diatomic N-B molecule.

Ionic liquids, designer solvents. Part 1: Comparison of selected 'onium' cations

Optimisation of [N(CH3)4]+, [P(CH3)4]+ and [S(CH3)3]+

[N(CH3)4]+ 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000038     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-2.905457D-10

Therefore, the optimisation is converged.


[P(CH3)4]+ 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000015     YES
 RMS     Force            0.000003     0.000010     YES
 Maximum Displacement     0.000037     0.000060     YES
 RMS     Displacement     0.000012     0.000040     YES
 Predicted change in Energy=-3.315353D-10

Therefore, the optimisation is converged.


[S(CH3)3]+ 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000019     0.000060     YES
 RMS     Displacement     0.000008     0.000040     YES
 Predicted change in Energy=-5.948627D-11

Therefore, the optimisation is converged.

Properties of atoms
Electronegativity Atomic diameter (Å)
Nitrogen 3.04 1.3
Sulphur 2.58 2.0
Carbon 2.55 1.4
Phosphorus 2.19 2.0
Hydrogen 2.20 0.5


Optimisation summary
[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
Structure
File Name nl_mlc1_opt_631g_dp_2 NL_MLC2_OPT2_631G_DP NL_MLC3_OPT_631G_DP_PG
File Type .log .log .log
Optimisation file link File:NL MLC1 OPT 631G DP 2.LOG File:NL MLC2 OPT2 631G DP.LOG File:NL MLC3 OPT 631G DP PG.LOG
Calculation Type FOPT FOPT FOPT
Calculation Method RB3LYP RB3LYP RB3LYP
Basis Set 6-31G(d,p) 6-31G(d,p) 6-31G(d,p)
Charge 1 1 1
Spin Singlet Singlet Singlet
E(RB3LYP) -214.18127441 a.u. -500.82701287 a.u. -517.68327437 a.u.
RMS Gradient Norm 0.00000299 a.u. 0.00000569 a.u. 0.00000109 a.u.
Dipole Moment 0.00 Debye 0.00 Debye 8.69 Debye
Point Group C1 C1 C1
Job cpu time 12 minutes 25.0 seconds 6 minutes 29.0 seconds 5 minutes 53.0 seconds
Geometry of molecules
[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
X-C bond distance (Å) 1.51 1.82 1.82
C-H bond distance (Å) 1.09 1.09 1.09
C-X-C bond angle (°) 109.5 109.5 102.7
H-C-H bond angle (°) 110.0 109.0 111.1

Note: 1) X = N, P and S respectively

In [N(CH3)4]+, the N atom is sp3 hybridised, resulting in the C-N-C bond angle of 109.5° and a tetrahedral geometry of the molecule. The sp3 hybrid orbitals are arranged as furthest as possible from each other in space in order to minimise the repulsion between the occupied electron pairs. Likewise, the P atom in [P(CH3)4]+ is sp3 hybridised and hence, the C-P-C bond angles are 109.5° and the molecule adopts a tetrahedral geometry as well. In the case of [S(CH3)3]+, the S atom is also sp3 hybridised. However, the lone pair of electrons on the S atom strongly repels with the bonding electrons. This causes the C-S-C bond angle to be 102.7° instead of the ideal 109.5° in a typical tetrahedral molecule. This can be rationalised by the need to minimise the repulsion between the lone pair and the bonding electrons. Thus, the C-S-C bond angle is smaller than the C-N-C and C-P-C angles, and the molecule adopts a near-tetrahedral geometry.

The shorter distance of C-N bond may be rationalised by looking at the atomic sizes. As the C and N atoms are very similar in atomic diameter, thus the atomic radii, they have good orbital size match and thus, the orbital overlap is efficient. This results in the shortening of the C-N bond and the high strength of the bond. Because P and S are much bigger in size than C, the orbital overlap in the C-P and C-S bonds are not as efficient and hence, these bonds are much longer and weaker than the C-N bond.

Frequency analysis

The frequency analysis was carried out using the same method and basis set combination as that used in the optimisation step for the reason mentioned previously. The analysis was carried out to ensure that the optimisation step gives the minimum structures. From the results, optimisation of the three molecules resulted in minimum structures as it can be seen that the first "Low frequencies" line of the three molecules have all the values close to zero and are within 15 cm-1 of each other. Furthermore, the second "Low frequencies" line shows no negative frequencies.

[N(CH3)4]+

6-31G(d,p) [N(CH3)4]+ frequency analysis file link: File:NL MLC1 OPT 631G DP FREQ3.LOG

Real output 

Low frequencies ---   0   0    0    0    3   11
Low frequencies ---  183  289  289


[P(CH3)4]+

6-31G(d,p) [P(CH3)4]+ frequency analysis file link: File:NL MLC2 OPT2 631G DP FREQ.LOG

Real output 

Low frequencies ---   -8   0   0   0    9   13
Low frequencies ---  156  192  192


[S(CH3)3]+

6-31G(d,p) [S(CH3)3]+ frequency analysis file link: File:NL MLC3 OPT 631G DP PG FREQ.LOG

Real output 

Low frequencies ---   -7   -6   0    0    0    10
Low frequencies ---  162  199  200

MO analysis

[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
Population analysis file link File:NL MLC1 OPT 631G DP 2 POP.LOG File:NL MLC2 OPT2 631G DP POP.LOG File:NL MLC3 OPT 631G DP PG POP.LOG


Molecular orbitals of [N(CH3)4]+
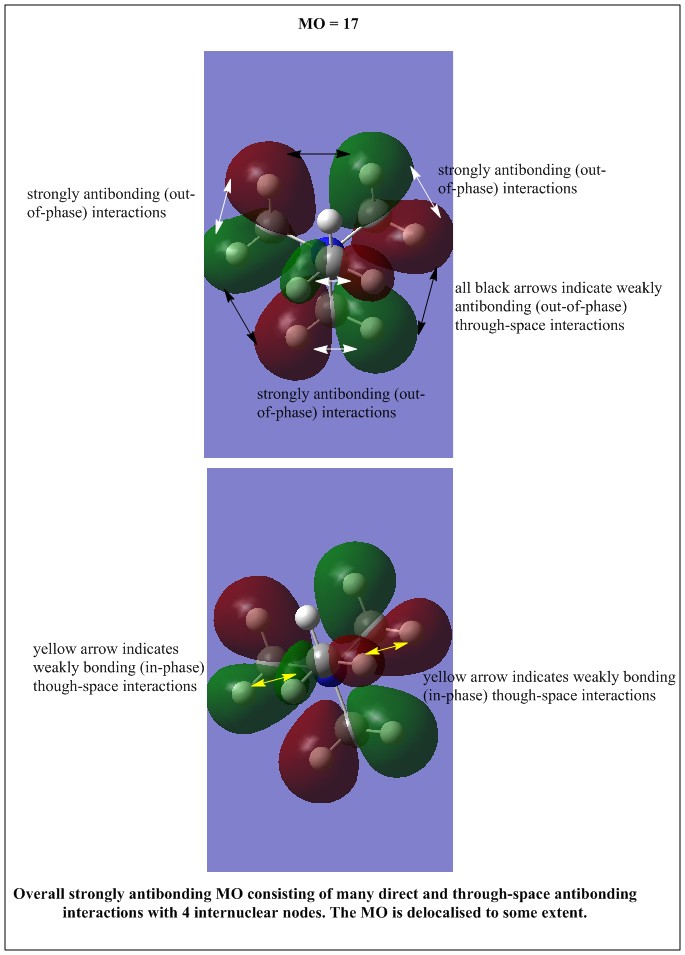
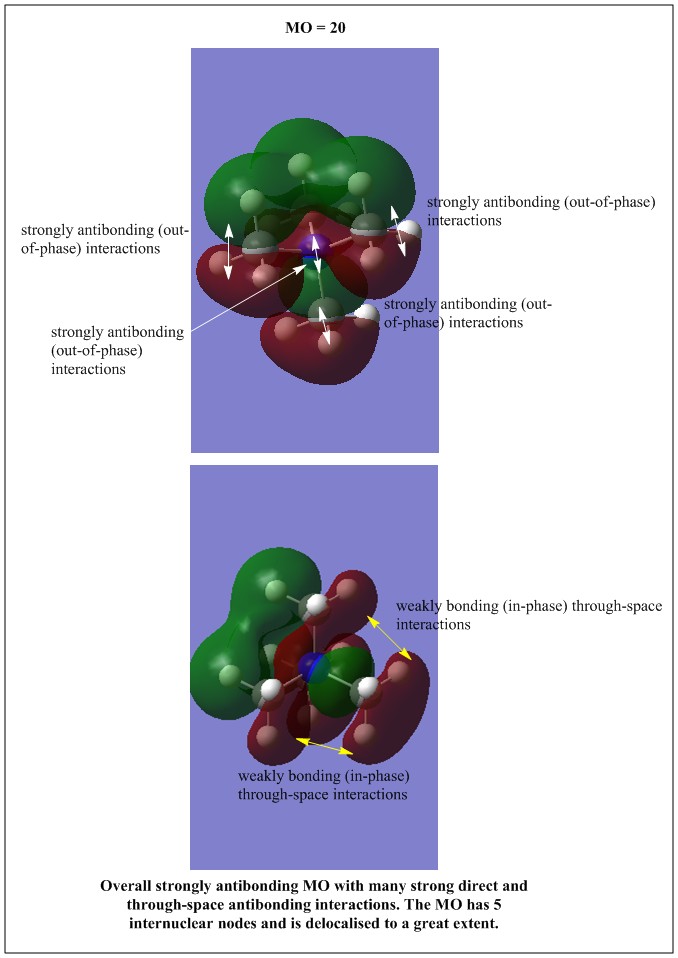
Occupied MO number Real MO Occupied MO number Real MO Occupied MO number Real MO Occupied MO number Real MO
7 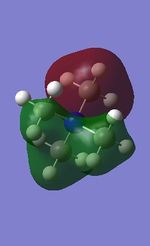8 9
10 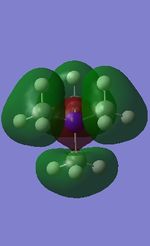11 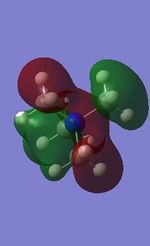12 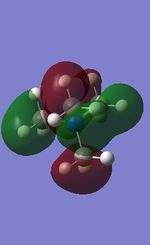13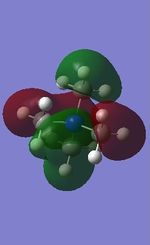
14 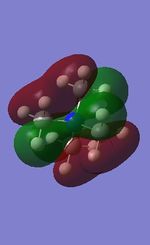15 16 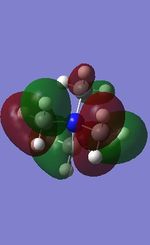17
18 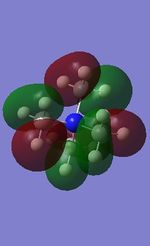19 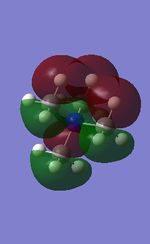20 21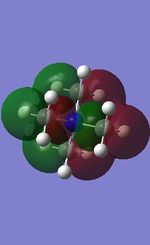

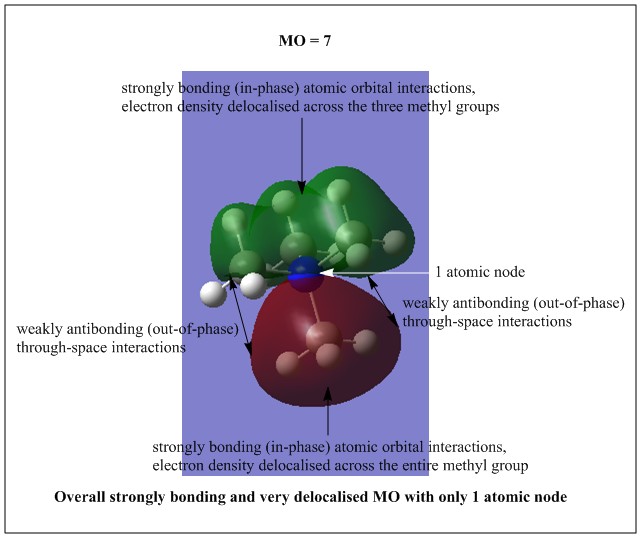
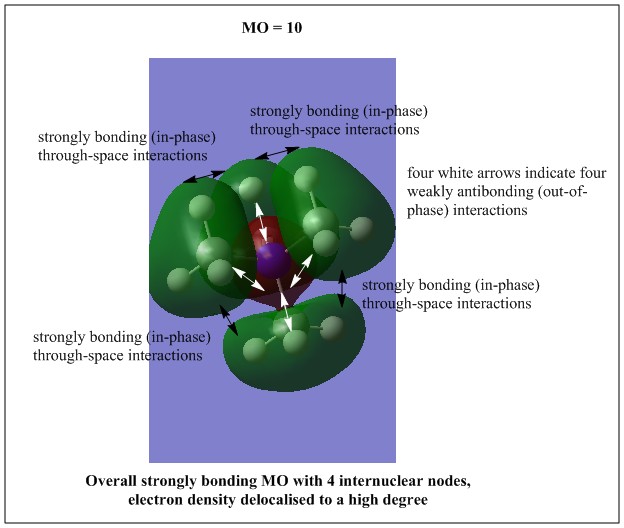
All the occupied non-core MOs of [N(CH3)4]+ are presented in the table above. The first occupied non-core MO starts from MO number 7. Non-core MOs are higher in energy than the core MOs, which are very deep in energy. Non-core MOs can be distinguished by the fact that the electron density is not localised at any of the atom but instead, is smeared out across the molecule. Furthermore, in non-core MOs, there are antibonding interactions of the atomic orbitals (MOs showing both red and green regions). The MO Theory is used to predict the electronic distribution of a molecule, which can then be used to predict the shape, bonding and reactivity of the molecule.

Five occupied, non-core MOs are picked and analysed in terms of bonding/antibonding character and are presented ranging from the most highly bonding to the most highly antibonding MO. MOs with the more antibonding character are more destabilised and are therefore, higher in energy.

NBO analysis

[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
NBO analysis
Charge distribution
Charge range

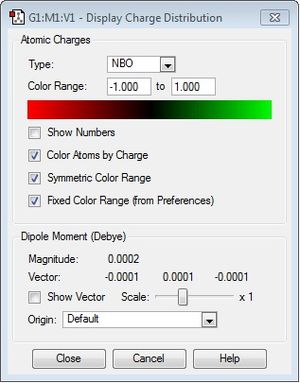
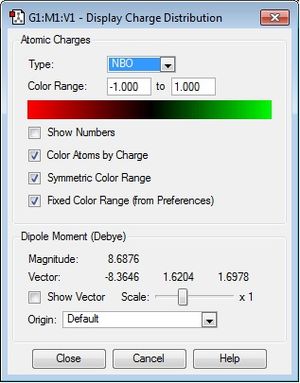
The charge range is -1.000 to 1.000 and is the same for all NBO diagrams. Therefore, comparisons of the charge distribution of the three cations can be compared.

NBO charges of atoms
[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
X (= N, P, S) -0.295 1.667 0.917
C -0.483 -1.060 -0.846
H 0.269 0.298 0.297

Note:

1) All C atoms in the each molecule have the same NBO charge

2) All H atoms in the each molecule have the same NBO charge


[N(CH3)4]+ 

(Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.99118) BD ( 1) C   1 - H   2  
                ( 63.47%)   0.7967* C   1 s( 26.42%)p 2.78( 73.53%)d 0.00(  0.05%)
                                            0.0000  0.5140  0.0032 -0.0004  0.7580
                                            0.0056  0.3378 -0.0233  0.2144 -0.0111
                                            0.0158  0.0095  0.0050  0.0094 -0.0084
                ( 36.53%)   0.6044* H   2 s( 99.95%)p 0.00(  0.05%)
                                            0.9997  0.0006 -0.0220 -0.0054 -0.0041
     4. (1.98452) BD ( 1) C   1 - N  17  
                ( 33.65%)   0.5801* C   1 s( 20.78%)p 3.81( 79.06%)d 0.01(  0.16%)
                                            0.0003  0.4552 -0.0237  0.0026 -0.6319
                                           -0.0268  0.5754  0.0244  0.2424  0.0103
                                           -0.0324 -0.0136  0.0124  0.0030 -0.0158
                ( 66.35%)   0.8146* N  17 s( 25.00%)p 3.00( 74.97%)d 0.00(  0.03%)
                                            0.0000  0.5000 -0.0007  0.0000  0.6159
                                           -0.0001 -0.5608  0.0001 -0.2363  0.0000
                                           -0.0142 -0.0060  0.0055  0.0013 -0.0069


[P(CH3)4]+ 

       (Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.98385) BD ( 1) C   1 - H   2  
                ( 64.78%)   0.8049* C   1 s( 24.88%)p 3.02( 75.08%)d 0.00(  0.04%)
                                           -0.0001  0.4987 -0.0070  0.0005 -0.0451
                                           -0.0216  0.5753  0.0024  0.6460  0.0033
                                            0.0028  0.0031  0.0183 -0.0065  0.0061
                ( 35.22%)   0.5934* H   2 s( 99.95%)p 0.00(  0.05%)
                                            0.9998  0.0008  0.0043 -0.0143 -0.0162
     4. (1.98031) BD ( 1) C   1 - P  17  
                ( 59.57%)   0.7718* C   1 s( 25.24%)p 2.96( 74.67%)d 0.00(  0.08%)
                                            0.0002  0.5021  0.0171 -0.0020  0.8280
                                           -0.0152 -0.1520  0.0028 -0.1945  0.0036
                                           -0.0085 -0.0109  0.0020  0.0223 -0.0123
                ( 40.43%)   0.6358* P  17 s( 25.00%)p 2.97( 74.15%)d 0.03(  0.85%)
                                            0.0000  0.0001  0.5000 -0.0008  0.0000
                                            0.0000 -0.8252  0.0012  0.0000  0.1515
                                           -0.0002  0.0000  0.1939 -0.0003 -0.0270
                                           -0.0345  0.0063  0.0709 -0.0391


[S(CH3)3]+ 

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.98721) BD ( 1) C   1 - H   2  
                ( 64.83%)   0.8051* C   1 s( 26.50%)p 2.77( 73.45%)d 0.00(  0.05%)
                                            0.0000  0.5147 -0.0056  0.0006 -0.2939
                                           -0.0154  0.8047 -0.0062  0.0196  0.0002
                                           -0.0057  0.0003 -0.0001 -0.0176 -0.0121
                ( 35.17%)   0.5931* H   2 s( 99.95%)p 0.00(  0.05%)
                                            0.9997  0.0011  0.0116 -0.0198  0.0001
     4. (1.98631) BD ( 1) C   1 - S  13  
                ( 48.67%)   0.6976* C   1 s( 19.71%)p 4.07( 80.16%)d 0.01(  0.14%)
                                            0.0003  0.4437  0.0140 -0.0033  0.8909
                                           -0.0030  0.0440  0.0056 -0.0763 -0.0098
                                            0.0032 -0.0055  0.0001  0.0316 -0.0183
                ( 51.33%)   0.7165* S  13 s( 16.95%)p 4.86( 82.42%)d 0.04(  0.63%)
                                            0.0000  0.0001  0.4117 -0.0076  0.0012
                                            0.0000 -0.8976  0.0258  0.0000 -0.0642
                                           -0.0179  0.0000  0.1112  0.0311  0.0162
                                           -0.0281 -0.0041  0.0639 -0.0342


Because the molecule is symmetrical around the central X atom, all C-X bonds are equivalent and so only one C-X bond in each molecule needs to be discussed. Besides, all three molecules have the C atoms attached to only H atoms and therefore, the effect of the electronegativity and size of the H atoms can be neglected in the analysis. Furthermore, all C-X bonds are occupied and so they all have an occupancy near to 2.00. Here, the relative contribution of the C atom and the heteroatom X to the C-X bond of the three cations is discussed and compared.

For each C-N bond in [N(CH3)4]+, the C orbitals, with a hybridisation of 21%s+79%p, contribute 34% to the bond, whilst the N orbitals, with a hybridisation of 25%s+75%p, contribute 66% to the bond. Hence, each of the 4 sp3 hybridised orbitals of the N atom interacts with the hybrid orbital of each C atom. As N has a higher electronegativity value than C (3.04 vs 2.55), the shared e- pair is pulled towards the N atom, meaning that the dipole moment also points towards the N atom and the resulting C-N bond is polar. This is consistent with the NBO analysis of the C-N bond as the N orbitals contribute more to the bond than the C orbitals. However, this contradicts with the NBO charge distribution analysis computed across the entire molecule because the e- pair in the C-N bond is expected to be pulled towards the N atom as N is more electronegative. However, the NBO charge distribution analysis reveals the charge of N to be -0.295, which is lower than the charge of -0.483 of the C atom (the lower the NBO charge, the more electronegative the atom). Moreover, looking from the colours of the C and N atoms, C has a slightly brighter red colour, supporting the statement further. Therefore, from this result, the electron density is higher around the C atoms than the N atom.

The C-P bond in [P(CH3)4]+ is attributed to ca. 60% C orbitals with 25%s+75% hybridisation and ca. 40% P orbitals with 25%s+74%p+1%d hybridisation. P has an electronegativity value of 2.19, whereas C has an electronegativity of 2.55. Thus, P is more electronegative and unlike [N(CH3)4]+, the C-P bond is polarised towards the C atom. This indicates that the electron density is much higher around the C atom and so the description that the positive charge is at the P atom can be justified as it is a region of low electron density. This is in good agreement with the NBO bond analysis as C contributes a little more to the C-P bond than P (60% vs 40%). Additionally, the NBO charge distribution analysis also shows that the P atom has an NBO charge of 1.667, whilst the C atom has a much lower NBO charge of -1.060, indicating a more electronegative C atom, and by inspecting the colours of the C and P atoms, the first statement is further supported as it can be seen that the P atom is very bright green (very electropositive), whilst the C atom is rather bright red (very electronegative). This concludes that the analysis using the electronegativity is consistent with the results obtained from the NBO analysis i.e. the C-P bond is polarised towards the C atom.

The C-S bond in [S(CH3)3]+ is attributed to ca. 49% C orbitals with 20%s+80%p hybridisation and ca. 51% S orbitals with 17%s+82%p+1%d hybridisation. Unlike all previous molecules, the two main atoms in [S(CH3)3]+, C and S are very near in the Periodic Table and hence, have very close electronegativity values (2.55 and 2.58 respectively). Therefore, the C-S bond should theoretically be less polar than both C-N and C-P bonds, even though the bonding e- pair is not equally shared as the bond is slightly polarised towards the S atom. This essentially conforms with the NBO bond analysis as the contribution of the C and S orbitals to the bond is almost equal (49% vs 51%). However, the NBO charge distribution analysis reveals otherwise. Even though an S atom on its own is slightly more electronegative than a C atom on its own, when in this cationic form, the C atoms become much more electronegative than the S atom (NBO charge of -0.846 vs 0.917). The colours of the atoms also reveal the C atom to be very electronegative (bright red) and the S atom to be much more electropositive (bright green).

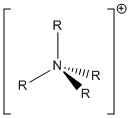
The fact that [NR4]+ (R=alkyl) is often depicted with the positive charge place on the central N atom is rather invalid and gives an inaccurate interpretation of the molecule. This is because based on the NBO analysis results of the [N(CH3)4]+, the C and N atoms are both rather electronegative (both red in colour) and thus, the positive charge should neither be placed on the central N atom nor the C atom. The traditional picture of the [NR4]+ molecule only has the formal positive charge placed on the N to represent the overall positive charge of +1 of the whole molecule. Since the C and N atoms in [NR4]+ are expected to be electronegative, as with the case with [N(CH3)4]+, only the H atoms in the molecule are electropositive. However, due to a big number of H atoms in the molecule, it would be inappropriate to place the positive charge on either one of the H atoms. Therefore, the structure of the [NR4]+ molecule may be best drawn using a bracket with the positive charge outside the bracket as shown below.


Several factors determine the energy and distance of the bond. These include atomic sizes of the two bonding atoms, their electronegativity difference and their electron affinities. The difference in electronegativity between the bonding C and X atoms (X = N,P,S) in the three molecules gives rise to distinct bond energies of the three. Shown below is the summary of C-X bond energy for each molecule. As C and N have the biggest electronegativity difference, the C-N bond, with the energy of -0.90688 a.u., is the most stable, which results in the bond having the shortest length of 1.51 Å. The C-P and C-S bonds having similar bond energies of -0.78614 and -0.83004 a.u. respectively, is a result of a similar difference in electronegativity between the C and X atoms, as well as the similarity in atomic diameters of P and S (both having a diameter of 2.0 Å). This eventually causes the C-P and C-S bonds to have the same bond distance of 1.82 Å. 

Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (C4H12N)
     1. BD (   1) C   1 - H   2          1.99118    -0.71141  127(v)
     2. BD (   1) C   1 - H   3          1.99118    -0.71141  135(v)
     3. BD (   1) C   1 - H   4          1.99118    -0.71141  131(v)
     4. BD (   1) C   1 - N  17          1.98452    -0.90688  44(v),125(v),129(v),133(v)
                                                    88(v),66(v),127(g),131(g)
                                                    135(g),67(v)
     5. BD (   1) C   5 - H   6          1.99118    -0.71142  135(v)
     6. BD (   1) C   5 - H   7          1.99118    -0.71141  123(v)
     7. BD (   1) C   5 - H   8          1.99118    -0.71141  131(v)
     8. BD (   1) C   5 - N  17          1.98452    -0.90689  66(v),22(v),134(v),120(v)
                                                    128(v),88(v),131(g),135(g)
                                                    123(g)
     9. BD (   1) C   9 - H  10          1.99118    -0.71141  127(v)
    10. BD (   1) C   9 - H  11          1.99118    -0.71141  123(v)
    11. BD (   1) C   9 - H  12          1.99118    -0.71141  135(v)
    12. BD (   1) C   9 - N  17          1.98452    -0.90688  89(v),45(v),23(v),122(v)
                                                    126(v),132(v),123(g),127(g)
                                                    135(g)
    13. BD (   1) C  13 - H  14          1.99118    -0.71141  131(v)
    14. BD (   1) C  13 - H  15          1.99118    -0.71141  123(v)
    15. BD (   1) C  13 - H  16          1.99118    -0.71140  127(v)
    16. BD (   1) C  13 - N  17          1.98452    -0.90689  67(v),121(v),130(v),124(v)
                                                    44(v),22(v),123(g),127(g)
                                                    131(g),23(v)




 Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (C4H12P)
     1. BD (   1) C   1 - H   2          1.98385    -0.69147  139(v)
     2. BD (   1) C   1 - H   3          1.98385    -0.69147  135(v)
     3. BD (   1) C   1 - H   4          1.98385    -0.69147  131(v)
     4. BD (   1) C   1 - P  17          1.98031    -0.78614  139(g),131(g),135(g),128(v)
                                                    136(v),133(v)
     5. BD (   1) C   5 - H   6          1.98385    -0.69147  127(v)
     6. BD (   1) C   5 - H   7          1.98385    -0.69148  135(v)
     7. BD (   1) C   5 - H   8          1.98385    -0.69147  139(v)
     8. BD (   1) C   5 - P  17          1.98031    -0.78615  135(g),127(g),139(g),132(v)
                                                    126(v),137(v)
     9. BD (   1) C   9 - H  10          1.98385    -0.69147  131(v)
    10. BD (   1) C   9 - H  11          1.98385    -0.69147  127(v)
    11. BD (   1) C   9 - H  12          1.98385    -0.69147  139(v)
    12. BD (   1) C   9 - P  17          1.98031    -0.78613  131(g),127(g),139(g),129(v)
                                                    138(v),125(v)
    13. BD (   1) C  13 - H  14          1.98385    -0.69147  127(v)
    14. BD (   1) C  13 - H  15          1.98385    -0.69147  131(v)
    15. BD (   1) C  13 - H  16          1.98385    -0.69147  135(v)
    16. BD (   1) C  13 - P  17          1.98030    -0.78613  127(g),135(g),131(g),124(v)
                                                    130(v),134(v)




 Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (C3H9S)
     1. BD (   1) C   1 - H   2          1.98721    -0.72255  105(v),89(v)
     2. BD (   1) C   1 - H   3          1.98721    -0.72255  109(v),89(v)
     3. BD (   1) C   1 - H   4          1.99412    -0.72709   
     4. BD (   1) C   1 - S  13          1.98631    -0.83004  102(v),107(v),105(g),109(g)
     5. BD (   1) C   5 - H   7          1.98721    -0.72255  101(v)
     6. BD (   1) C   5 - H   8          1.99412    -0.72709   
     7. BD (   1) C   5 - H   9          1.98721    -0.72255  109(v),90(v)
     8. BD (   1) C   5 - S  13          1.98631    -0.83008  98(v),108(v),101(g),109(g)
     9. BD (   1) C   6 - H  10          1.99412    -0.72709   
    10. BD (   1) C   6 - H  11          1.98721    -0.72255  101(v)
    11. BD (   1) C   6 - H  12          1.98721    -0.72255  105(v),90(v)
    12. BD (   1) C   6 - S  13          1.98631    -0.83005  99(v),104(v),105(g),101(g)

Ionic liquids, designer solvents. Part 2: Influence of functional groups

Optimisation of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+

[N(CH3)3(CH2OH)]+ 

        Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000059     0.000060     YES
 RMS     Displacement     0.000015     0.000040     YES
 Predicted change in Energy=-1.260212D-10

Therefore, the optimisation is converged.


[N(CH3)3(CH2CN)]+ 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000013     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-6.528655D-12

Therefore, the optimisation is converged.


Optimisation summary
[N(CH3)3(CH2OH)]+ [N(CH3)3(CH2CN)]+
Structure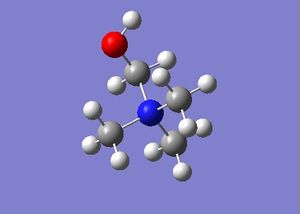
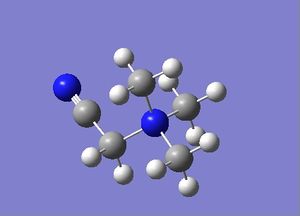
File Name NL_MLC4_OPT_631G_DP NL_MLC5_OPT_631G_DP
File Type .log .log
Optimisation file link File:NL MLC4 OPT 631G DP.LOG File:NL MLC5 OPT2 631G DP.LOG
Calculation Type FOPT FOPT
Calculation Method RB3LYP RB3LYP
Basis Set 6-31G(d,p) 6-31G(d,p)
Charge 1 1
Spin Singlet Singlet
E(RB3LYP) -289.39470755 a.u. -306.39376117 a.u.
RMS Gradient Norm 0.00000153 a.u. 0.00000032 a.u.
Dipole Moment 10.40 Debye 8.67 Debye
Point Group C1 C1
Job cpu time 18 minutes 34.0 seconds 12 minutes 16.0 seconds

Frequency analysis

The frequency analysis was carried out using the same method and basis set combination as that used in the optimisation step for the reason mentioned previously.

[N(CH3)3(CH2OH)]+

6-31G(d,p) [N(CH3)3(CH2OH)]+ frequency analysis file link: File:NL MLC4 OPT 631G DP FREQ.LOG

Real output 

Low frequencies ---   -9   -5   0   0   0    5
Low frequencies ---  131  214  256


[N(CH3)3(CH2CN)]+

6-31G(d,p) [N(CH3)3(CH2CN)]+ frequency analysis file link: File:NL MLC5 OPT2 631G DP FREQ.LOG

Real output 

Low frequencies ---   -6   -5   0    0    0    7
Low frequencies ---   92  154  211

MO analysis

[N(CH3)3(CH2OH)]+ [N(CH3)3(CH2CN)]+
Population analysis file link File:NL MLC4 OPT 631G DP POP.LOG File:NL MLC5 OPT2 631G DP POP.LOG
HOMO and LUMO of [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+
[N(CH3)4]+ [N(CH3)3(CH2OH)]+ [N(CH3)3(CH2CN)]+
HOMO
Energy of HOMO (a.u.) -0.57934 -0.48763 -0.50047
LUMO
Energy of LUMO (a.u.) -0.13302 -0.12459 -0.18183
HOMO-LUMO gap (a.u.) 0.44632 0.36304 0.31864

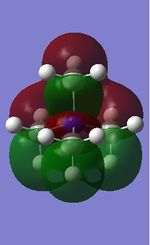
From the "real" HOMOs of the three molecules, it can be seen that the HOMO of [N(CH3)4]+ is the most delocalised, whilst the HOMO of [N(CH3)3(CH2CN)]+ is the least delocalised. This can be rationalised by the modification of one of the ligands, from CH3 to CH2OH and CH2CN. The CH3 group is electron-donating, whilst both the CH2OH and CH2CN groups are electron-withdrawing. However, because of the more electronegative N atom in CH2CN, this group is much more electron-withdrawing than the CH2OH group containing the less electronegative O atom. This means that both CH2OH and CH2CN groups withdraw electron density from the system but with the electron density being removed to a greater extent when the ligand is CH2CN. The HOMO of [N(CH3)3(CH2CN)]+ has its electron density removed almost completely from the three CH3 ligands, with the region of highest electron density around the C=N. This also applies similarly to the case of [N(CH3)3(CH2OH)]+, where the electron density is the highest around the O-H and the lowest around the remaining three ligands. However, the electron density is removed to a lesser extent. Conversely, because CH3 is an electron-donating group, the HOMO of [N(CH3)4]+ is very delocalised. Whilst the HOMO energy of [N(CH3)4]+ is very low, the energies of the HOMO of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ are much higher and are rather similar.

The shapes of the LUMO of the first two cations, [N(CH3)4]+ and [N(CH3)3(CH2OH)]+ are similar, with the electron density delocalised quite evenly across the whole structure. This is also because the geometries of these two molecules are quite similar. However, the electron density is slightly less delocalised across [N(CH3)3(CH2OH)]+ due to the presence of an electron-withdrawing CH2OH group. The energy of the LUMOs of [N(CH3)4]+ and [N(CH3)3(CH2OH)]+ are therefore very close. In the case of [N(CH3)3(CH2CN)]+, the electron density is delocalised across the entire structure as well, however, because of the C-N triple bond, the geometry of this cation is quite different to the other two cations and the LUMO energy is the lowest of the three.

Whilst electron-donating groups increase the energy of MOs in general, the electron-withdrawing groups decrease the energy of the MOs. This means that molecules containing electron-donating groups have their HOMO and LUMO energy increased, whereas molecules containing electron-withdrawing groups have their HOMO and LUMO lower in energy. This is reflected in the energies obtained for the HOMO and LUMO of the three cations. Going from [N(CH3)4]+ to [N(CH3)3(CH2OH)]+ and then to [N(CH3)3(CH2CN)]+, the (CH3) is substituted with an increasingly electron-withdrawing group, CH2OH and CH2CN respectively and thus, the HOMO-LUMO gap decreases significantly.

According to Walsh's rule, the molecule will adopt the structure where the HOMO is most stabilised, leading to a maximised HOMO-LUMO gap. The maximisation of the HOMO-LUMO gap is directly relevant to the reactivity of the molecule. In the reaction of two molecules, the HOMO of one molecule interacts with the LUMO of the other molecule. Therefore, if there is good energy match between the HOMO of the first molecule and the LUMO of the second molecule, the reaction is likely to be favoured and successful due to the overall lowering of energy. Ideally, this means that the HOMO of the first molecule should be very high in energy, whilst the LUMO of the second molecule should be very low in energy.

Because the three molecules are based on quaternary ammonium cations, they all act as Lewis acids. Lewis acids can accept an electron pair from a compound with high energy HOMO (Lewis base). This implies that strong Lewis acids should have a substantially low-lying LUMO. Conforming with this statement, this suggests that [N(CH3)3(CH2CN)]+ is the strongest Lewis acid (lowest LUMO energy) and [N(CH3)3(CH2OH)]+ is the weakest Lewis acid of the three (highest LUMO energy). Hence, due to the low-lying LUMO of [N(CH3)3(CH2CN)]+, the C-N triple bond is most subject to attack by Lewis bases (nucleophiles) with high energy HOMOs. Although CH2OH is more electron-withdrawing than the CH3 group and one may anticipate for the LUMO in [N(CH3)3(CH2OH)]+ to be lower in energythan that in [N(CH3)4]+, however, this may not be the case. The reason may be due to the fact that there is more repulsion between the substituents in [N(CH3)3(CH2OH)]+ and this repulsion outweighs the decrease in the MO energies overall.

By using computer simulation to predict the energy of the HOMO and LUMO of molecules, one can investigate the reaction of different functional groups and thus, this method of analysis can prove to be very useful.

NBO analysis

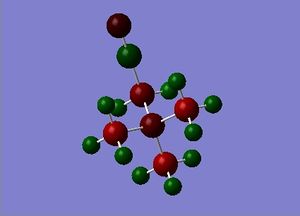
[N(CH3)3(CH2OH)]+ [N(CH3)3(CH2CN)]+
NBO analysis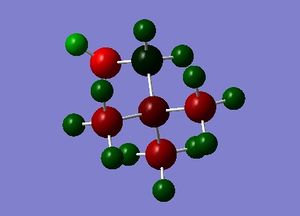
Charge distribution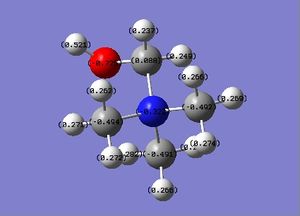
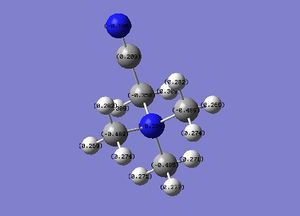
Charge range

The charge range is -1.000 to 1.000 and is the same for both NBO diagrams. Therefore, comparisons of the charge distribution of the two cations can be compared.

NBO charges of atoms
[N(CH3)3(CH2OH)]+ [N(CH3)3(CH2CN)]+
Central N atom -0.322 Central N atom -0.289
Methyl C atom (x3) -0.494, -0.491, -0.492 Methyl C atom (x3) -0.489
Methyl H atom (x9) 0.262-0.282 Methyl H atom (x9) 0.269-0.282
Methylene C atom 0.088 Methylene C atom -0.358
Methylene H atom (x2) 0.237, 0.249 Methylene H atom (x2) 0.309
Hydroxyl O -0.725 Nitrile C 0.209
Hydroxyl H 0.521 Nitrile N -0.186


"OH is an electron-donating group and CN is an electron-withdrawing group."

Both OH and CN donates and withdraws electron respectively via inductive effects. The oxygen atom in OH is an electronegative atom containing two lone pairs of electrons. The OH group increases electron density in the system, whilst the CN group decreases electron density of the system. EDGs can help to stabilise cations, whereas EWGs can help to stabilise anions.

Therefore, if the above statement is true, it would be expected that in general, the electron density in [N(CH3)3(CH2OH)]+ would be increased with the C atom attached to the OH group more partially negative. However, the result does not support the statement as the negative charge is still highly concentrated on the O atom (O atom bearing a highly negative NBO charge) and the adjacent C atom is rather green in colour i.e. it bears a partial positive charge. Although the methyl C atoms are red, i.e. electronegative, this could be due to the central N atom which is very electronegative and not the inductive electron-donating effect of the OH group.

If the CN group is indeed electron-withdrawing as stated, the methylene C would be expected to appear green as the electron density is removed in the electron-withdrawing effect of the CN group. Furthermore, the fact that the methylene C is attached to the electronegative N atom, this C atom should bear a high partial positive charge, and thus bright green in colour. However, the result does not support the hypothesis as the methylene C atom is rather red in colour (NBO charge of -0.358) and even if it does, the fact that the CN group is electron-withdrawing in this case cannot be assured as the methylene C is also attached to the central N atom which is very electronegative and strongly pulls electron density towards itself.

References

  1. ↑ 1.0 1.1 CRC Handbook of Chemistry and Physics, ed. W. M. Haynes and D. R. Lide, CRC Press, Boca Raton, 92nd edn., 2011.
  2. ↑ IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). DOI:10.1351/goldbook
  3. ↑ S. Mebs, R. Kalinowski, S Grabowsky, D. Forster, R. Kickbusch, E. Justus, W. Morgenroth, C. Paulmann, P. Luger. D. Gabel and D. Lents, J. Phys. Chem. A., 2011, 115, 1385-1395.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:nl411&oldid=820354"