Rep:Mod:nk747

Module 2: Bonding (Ab initio and density functional molecular orbital)

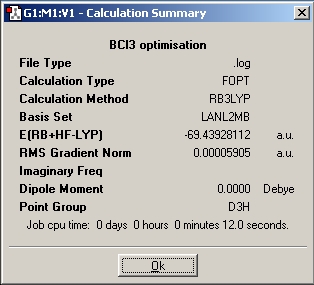
Boron trichloride, BCl₃

Optimised bond length: 1.86592Å

Optimised bond angle: 120°

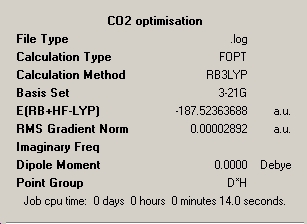
Carbon dioxide, CO₂

Optimised bond length: 1.18278Å

Optimised bond angle : 180°

xyz-coordinates

---------------------------------------------------------------------
Center     Atomic     Atomic              Coordinates (Angstroms)
Number     Number      Type              X           Y           Z
---------------------------------------------------------------------
   1          6             0        0.000000    0.000000    0.000000
   2          8             0        0.000000    0.000000    1.182781
   3          8             0        0.000000    0.000000   -1.182781
---------------------------------------------------------------------

Published optimised structure DOI:10042/to-1256

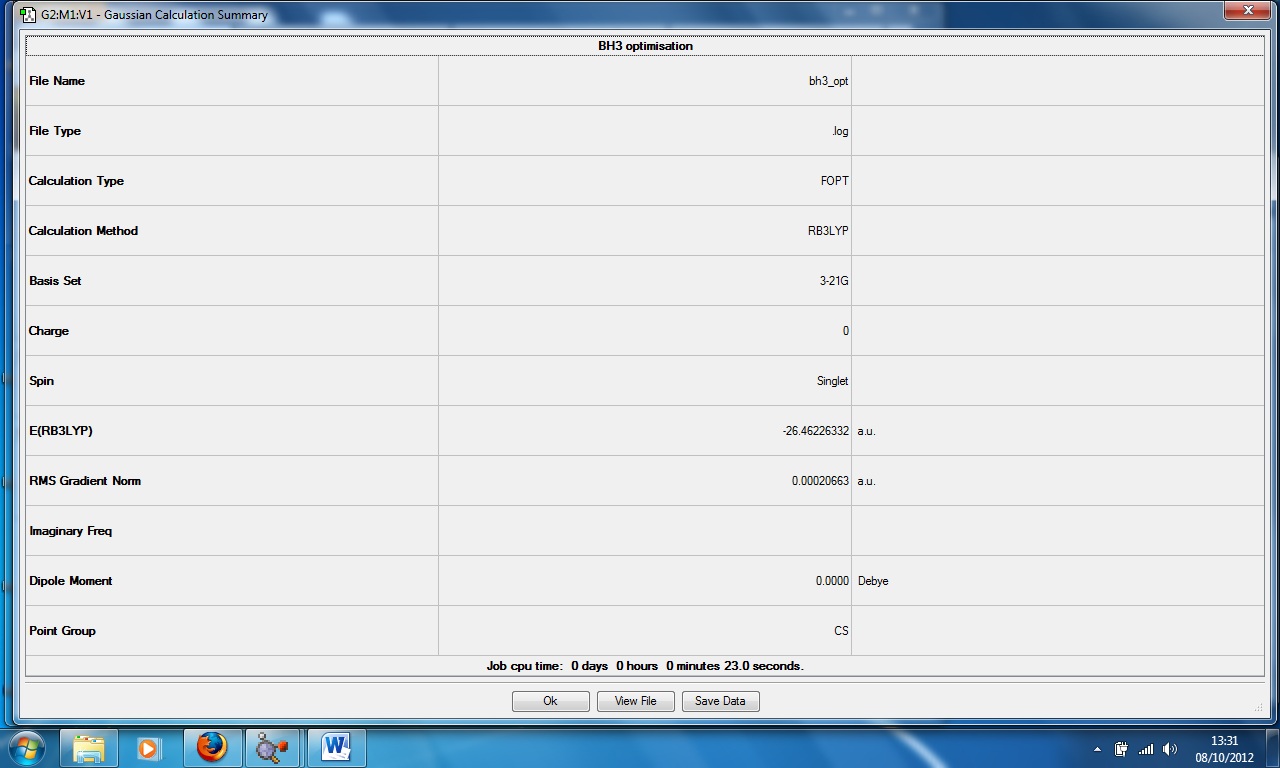
Borane, BH₃

Optimised bond length: 1.19435Å

Optimised bond angle: 120°

Vibrations

Form of vibration	Frequency/cm-1	Intensity	Symmetry
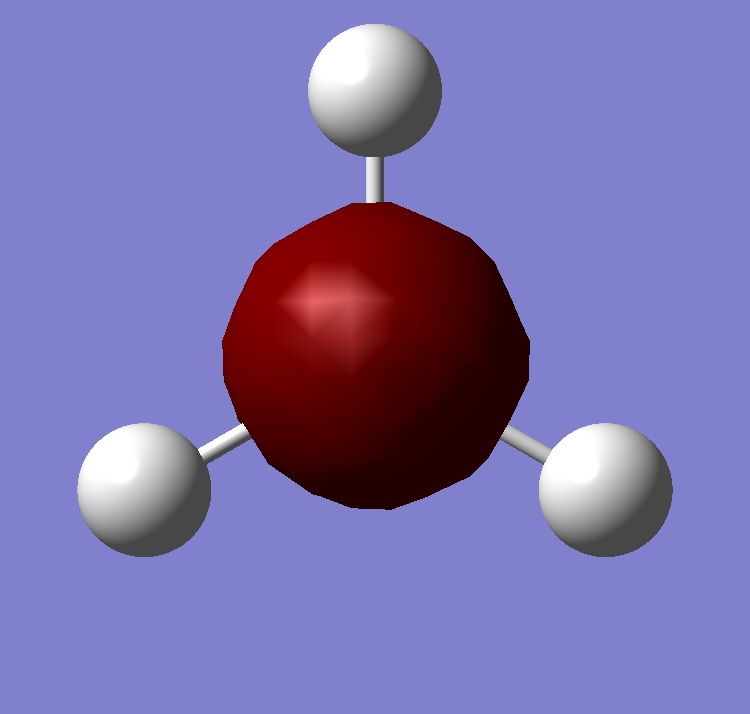	1145.71	92.6991	A2’’
	1204.66	12.3789	E’
	1204.66	12.3814	E’
	2592.79	0	A1’
	2731.31	103.837	E’
	2731.31	103.83	E’

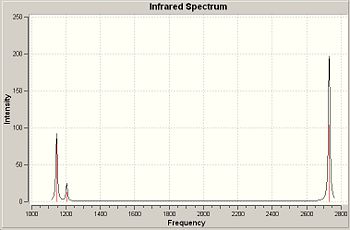
IR spectrum

Only 3 peaks are seen because one of the frequencies has an intensity of 0 while vibrations 2 and 3, and vibrations 5 and 6, have the same intensity.

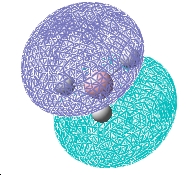
Molecular Orbitals

2a1	1e	1a2

The computed and qualitative molecular orbitals match each other well suggesting that molecular orbital theory is good at generating "guess" molecular orbitals.

Ammonia, NH₃

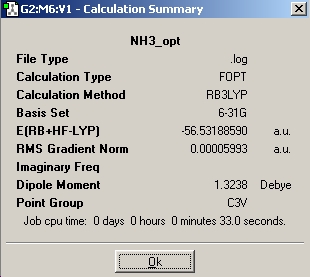
B3LYP optimisation

	C1	C3v	D3h
Calculation Summary
Energy (kJ/mol)	-148424.34	-148424.33	-148423.43

During an optimisation, the program will always try to keep the symmetry of the initial molecule the same, therefore more symmetrical molecules have shorter optimisation times because there are less ways to move the atoms. However, this does not occur when the ignore symmetry box is ticked hence the C1 molecule takes the longest to optimise followed by the C3v and then D3h. C1 is the lowest energy geometry; 0.01kJ/mol lower than C3v and 0.908kJ/mol lower than D3h.

Second order Jahn-Teller effects stabilises the more symmetrical molecules by distorting their geometries to lower symmetries which allows molecular orbital mixing to occur. As the D3h is the most symmetrical molecule, the least molecular orbital mixing occurs here (compared to the C1 molecule, which is the least symmetrical) resulting in it having the highest energy. This explains the order of the energies between the different symmetries.

MP2 optimisation

	C3v	D3h
Calculation Summary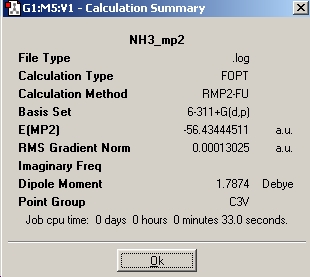
Energy (kJ/mol)	-148424.34	-148424.33

The higher level MP2 optimisations take longer than the lower level ones because the new optimisation produces a more accurate ammonia molecule.

The barrier height to inversion of ammonia is the difference in energy between the D3h molecule and the C3v molecule which equals 20.47kJ/mol for the MP2 optimisations but equals 0.908kJ/mol for the B3LYP optimisations. The experimentally determined value of the inversion is 24.3kJ/mol which tells us that a MP2 method much more reliable than a B3LYP method for optimising structures.

Ammonia is known to invert at room temperature even though there is only 2.48kJ/mol of thermal energy present at 298.15K (E=RT). The inversion occurs without the required 24.3kJ/mol because the hydrogens undergo quantum tunneling during the inversion mechanism.

Vibrational Analysis of C3v

Vibrational spectrum of C3v

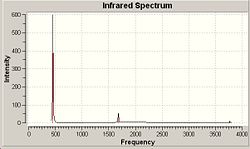
Number	Frequency/cm-1	Intensity	Symmetry
1	452.302	599.472	A1
2	1680.47	41.7256	E
3	1680.47	41.7245	E
4	3575.43	0.0683	A1
5	3775.76	7.0892	E
6	3775.76	7.0884	E

Vibrational Analysis of D3h

Vibrational spectrum of D3h

Number	Frequency/cm-1	Intensity	Symmetry
1	-381.051	849.113	A2
2	1640.59	55.9828	E'
3	1640.59	55.9805	E'
4	3635.71	0	A1'
5	3845.27	19.5951	E'
6	3845.27	19.5963	E'

The vibrational modes in the C3v and D3h molecules which have the same character of motion are vibrations 1, 2, 3 and 4. The vibrations which have different character of motion are 5 and 6.

The C3v molecule has all positive frequencies while the D3h molecule has one negative frequency, -318.051cm^-1. The negative frequency is present because the D3h molecule is the transition state of the inversion reaction path.

The only vibration in both molecules that follows the inversion path is vibration 1.

Frequency/cm-1	Literature Frequency/cm-1
452.302	932
1680.47	1626
1680.47	1626
3575.43	3337
3775.76	3444
3775.76	3444

All the frequencies match the literature frequencies well except for the first frequency. Previously, I found that the barrier height to inversion of ammonia in the B3LYP optimisation was only 0.908kJ/mol which was much lower than the experimental. Vibration 1 is also associated with the inversion of ammonia and is also much lower than its literature value. By considering these two points, I can conclude that the lower computed frequency of vibration 1 is due to the B3LYP method not optimising the ammonia well enough.

Isomers of Mo(CO)₄L₂

Published optimised cis-isomer: DOI:10042/to-1213

Published optimised trans-isomer: DOI:10042/to-1212

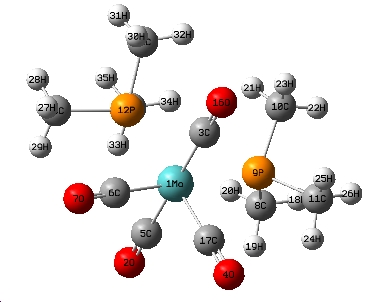
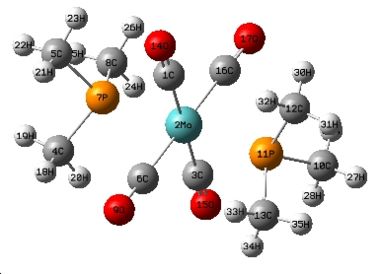
Cis-isomer geometry parameters

	Bond Length/Å	Literature Values/Å
Mo-P(9)	2.64775	2.522
Mo-P(12)	2.6482	2.522
Mo-C(6)	1.98217	1.966
Mo-C(17)	1.9819	1.975
Mo-C(5)	2.03251	2.022
Mo-C(3)	2.03265	2.042

Trans-isomer geometry parameters

	Bond Length/Å	Literature Values/Å
Mo-P(7)	2.57222	2.5
Mo-P(11)	2.57193	2.5
Mo-C(1)	2.02959	2.016
Mo-C(3)	2.02831	2.016
Mo-C(16)	2.02891	2.0005
Mo-C(6)	2.02762	2.005

In the cis isomer, the Mo-C bonds which are trans to the phosphine ligands are noticably shorter than the Mo-C bonds which are trans to the other carbonyl ligand. This is due to the carbonyl ligand having a larger trans effect than the phosphine ligand therefore the carbonyl ligand pulls electrons from the Mo-P bond, weakening the Mo-P bond and strenghtening the Mo-C bond. The weakened Mo-P bond is longer in the cis than in the trans isomer because there is no trans effect observed in the trans isomer. As the phosphine ligands are closer to each other in the cis isomer, there is a large amount of steric strain therefore the Mo-P bond is elongated in order reduce this. This elongation is not needed in the trans isomer because the phosphines are far apart.

	Cis	Trans
Computed bond angle	92.893°	178.042°
Literature bond angle	97.54°	180°

The bond angles and bond lengths are similar to the literature values therefore B3LYP/LANL2DZ was a good method of optimising the structures.

IR Frequencies

Published frequency calculation of cis-isomer: DOI:10042/to-1219

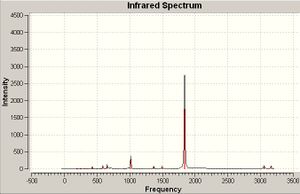
Cis isomer

Number	Frequency/cm-1	Literature Freq/cm-1	Intensity
78	1849.79	1886.8	1093.31
79	1850.94	1898.5	1948.78
80	1870.45	1913.7	653.212
81	1960.75	2012.4	336.45

Published frequency calculation of trans-isomer: DOI:10042/to-1220

Trans isomer

Number	Frequency/cm-1	Literature Freq/cm-1	Intensity
78	1839.55	1885.4	2002.81
79	1839.6	1885.4	2000.17
80	1883.15	1933.9	4.1744
81	1955.06	2050.4	1.918

The psuedo-symmetry of the cis and trans isomers are C2v and D4h respectively, therefore the cis isomer should have 4 carbonyl peaks whereas the trans isomer will have 3 carbonyl peaks. In the trans isomer, vibrations 78 and 79 have identical character of motion and share almost identical frequencies therefore they can be seen as degenerate vibrations, hence there are 3 carbonyl peaks for the trans isomer.

Total Energy of the Isomers

Cis	Trans
-2030455.20kJ/mol	-2030447.54kJ/mol

The trans isomer is more thermodynamically stable by 7.66kJ/mol, which matches the trend given in literature. This is most likely due to the large amounts of steric strain between the large phosphine groups in the cis-isomer causing an increase in its total energy. The phosphine groups in the trans isomer do not experience any steric strain.

Mini Project: Ammonia borane

Staggered and Eclipsed Conformers of Ammonia Borane and Ethane

Both the eclipsed and staggered conformers of ammonia borane were optimised in three stages, firstly using the B3LYP/3-21G method, then with 6-31G(d) basis set (at B3LYP level) and finally a MP2/6-311G(d,p) optimisation. From these calculations, the staggered conformation was found to be lower in energy due to less torsional strain. In order to produce the eclipsed structures, redundant coordinates were used to freeze the dihedral angle to zero degrees.

	Staggered	Eclipsed
jmol	Pentahelicene	Pentahelicene
Summary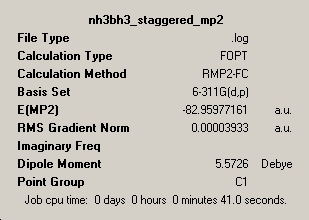
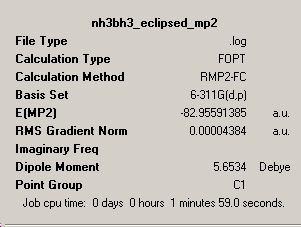
Energy (kJ/mol)	-217800.6	-217810.7

The eclipsed and staggered conformers of ethane were also optimised using the same methods as ammonia borane and the energies of both molecules compared.

	Staggered	Eclipsed
jmol	Pentahelicene	Pentahelicene
Summary
Energy (kJ/mol)	-208913.2	-208899.8

The energy difference between the staggered and eclipsed conformers of ammonia borane is 10.1285kJ/mol while for ethane it is 13.382kJ/mol. To explain this energy difference, the N-B and C-C bond lengths in ammonia borane and ethane respectively were observed:

	Ammonia borane		Ethane
	Staggered	Eclipsed	Staggered	Eclipsed
Bond length/Å	1.65389	1.68169	1.52859	1.54192
Literature bond lengths/Å	1.67225	-	1.5400	-

The shorter bond length in ethane is most likely due to better overlap between same sized orbitals of both carbon atoms. When a staggered conformer changes to an eclipsed one, the energy difference between each conformer is dependent on the change in bond length for each conformer; a larger difference in bond length gives a smaller difference in energy. This is because there is less torsional strain in the eclipsed structure when the distance between the eclipsing groups is large. In ammonia borane, the bond length difference between the staggered and eclipsed conformers is larger than the bond length difference in ethane so there is a smaller energy difference between the ammonia borane conformers. The N-B and C-C bond lengths match well with the literature values.

Bonding Analysis

MO in ammonia borane showing the empty p orbital on the boron interacting with the lone pair on nitrogen. MO in ethane showing the two sp3 orbitals of carbon interacting with each other.

Cartoon of bonding nature in ammonia borane and ethane.

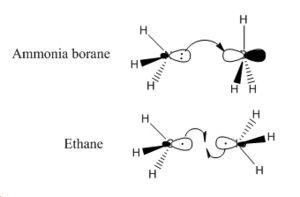
Whilst the type of bonding in ammonia borane and ethane are both covalent, they are different in that the N-B bond is formed via a lewis acid/base reaction and the C-C bond is formed by the sharing of electrons contributed by both carbons. The MO picture of ammonia borane shows the molecular orbital produced by the interaction of the lone pair of nitrogen with the empty p orbital of BH3; and the MO picture of ethane shows the molecular orbital produced when the unbonded, singly occupied sp3 orbitals from both CH₃ fragments interact.

Energy Analysis

The energies of NH₃BH₃ and each individual reacting substituent ie NH3 and BH3 were compared and a value for ΔE = E(product) - E(reactants) was obtained.

	NH3BH3	NH3	BH3
Energies (kJ/mol)	-217800.6	-148424.33	-69476.66

Therefore, ΔE = +100.39kJ/mol. The positive value of enthalpy means that the formation of ammonia borane from these substituents is an endothermic process, requiring the input of thermal energy into the system. As ammonia borane is not spontaneously formed, ammonia and BH₃ cannot be used to synthesise it therefore a different reaction is needed. From literature, a suitable synthesis is via a reaction between NH₄Cl and NaBH₄ to produce NH₄BH₄ followed by decomposition to give NH₃BH₃ and H₂.

Derivatives of Ammonia Borane

The next part of the project involved substituting the hydrogens on B and N with chlorine atoms, and running frequency, molecular orbital and charge distribution calculations on the optimised structure in order to compare the new compounds and seeing the effects of substituting hydrogens for chlorine.

	NCl3BH3	NH3BH3	NH3BCl3
jmol	Pentahelicene	Pentahelicene	Pentahelicene
NBO
Molecular orbitals
Vibration freq of N-B bond/cm-1	577.134	683.494	783.565

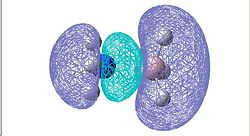
The vibration frequencies of the N-B bond in each of the three compounds were recorded and the corresponding MO picture showing the N-B bonding included in the table. Both NCl₃BH₃ and NH₃BCl₃ are compared to NH₃BH₃.

For NCl₃BH₃, the MO picture shows that there is an interaction between the Cl p-orbitals and the N lone pair orbital. Since chlorine is more electronegative than nitrogen, the nitrogen lone pair is pulled slightly towards the chlorine atoms and becomes more difficult to donate into the empty p-orbital of the boron. This reduction in electron density on the nitrogen atom is proved by the decrease in NBO charge compared to the NBO charge of NH₃BH₃. Due to the lone pair being less readily donated, the N-B bond weakens and hence the vibrational frequency is smaller.

In NH₃BCl₃, the electronegative chlorine pulls electrons from nitrogen via the N-B bond therefore boron has a more negative NBO charge than in NH₃BH₃. This results in the N-B bond containing a larger concentration of electrons, hence the N-B bond is stronger and the vibrational frequency larger.