Rep:Mod:nk1016
Intro to Molecular Modelling 2
Ammonia Molecule
Molecule: NH3
Optimisation
Gaussian is used to optimise the structure and it does this by measuring the energy of the molecule with the nuclei at different positions until it can't find a set of positions of a lower energy. This works best when there is only one minimum in potential energy.
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -56.55776873 au
RMS Gradient: 0.00000485 au
Point Group: C3V
Optimised N-H Bond Length: 1.01798 angstroms
Optimised H-N-H Bond Angle: 105.741 degrees
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
File:NKAILAYAPILLAI NH3 OPT POP.LOG
Ammonia |
Vibrations
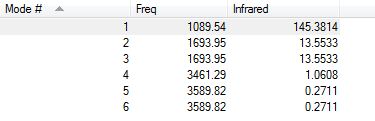
Below is the vibration information for ammonia
With the 3n-6 rule,(n=4), 6 different modes are expected.
Modes 2 and 3 are degenerate and modes 5 and 6 are degenerate (they have the same infrared values.
Modes 1,2 and 3 are bending and modes 4,5 and 6 are stretching.
Mode 4 is highly symmetric.
Mode 1 is the umbrella mode.
4 bands would be expected to be seen from an experimental spectrum of gaseous ammonia. The bands are caused by shifts in the dipole of the molecule during the various vibrations. There are 4 because the degenerate modes would appear as the same band and, as the shape of ammonia is trigonal pyramidal and not trigonal planar, the symmetric mode still causes a shift in dipole.
Charges
N-atom Charge: -1.125
H-atom Charge: 0.375
I would expect nitrogen to be negative and hydrogen to be positive as nitrogen is more electronegative than hydrogen so the bonding electrons should be closer to the nitrogen atom making it more negative and the hydrogen atoms more positive.
Making Ammonia
Nitrogen
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -109.52412868 au
RMS Gradient: 0.00000060
Point Group: D*H
Optimised N-N bond lenght: 1.10550 angstroms
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Below is the vibration information for nitrogen
Hydrogen
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -1.17853936 au
RMS Gradient: 0.00000017 au
Point Group: D*H
Optimised H-H bond length: 0.74279 angstroms
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Below is the vibration information for hydrogen
Reaction
In the Haber-Bosch process, 1 mole of nitrogen gas reacts with 3 moles of hydrogen gas to produce 2 moles of ammonia. Using the energy of the optimised forms of the molecules, the change in energy of the reaction can be worked out.
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
DeltaE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907
Energy for converting hydrogen and nitrogen gas into ammonia gas: -146.4784829 kJ/mol. The ammonia product is more stable than the gaseous reactants. The value found can be compared to a literature one of -50kJ/mol[1] This value is quite lower than the value calculated but this can be down to different conditions behind the 2 values.
Hydrogen Fluoride
Molecule: HF
Optimisation
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -100.42746153 au
RMS Gradient: 0.00001092 au
Point Group: C*V
Optimised H-F bond length: 0.92540 angstroms
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.000016 0.001800 YES RMS Displacement 0.000022 0.001200 YES
The Optimised Molecule |
Vibrations
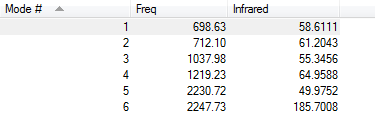
Below is the vibration information for HF
The mode is a reflexive stretch.
Charges
F-atom charge: -0.543
H-atom charge: 0.543
This result is expected as fluorine is more electronegative than hydrogen so would attract the electrons in the bond towards it, making it slightly negative and the hydrogen atom slightly positive.
Molecular Orbitals
This is an occupied non-bonding sigma molecular orbital made from solely the 2s atomic orbital of fluorine. It is deep in energy
This is an occupied bonding sigma molecular orbital made from the 1s atomic orbital from hydrogen and the 2pz atomic orbital from fluorine. It is relatively deep in energy
This is an unoccupied antibonding sigma* molecular orbital made from the same orbitals as above.
These are the occupied non-bonding pi molecular orbitals made from only the 2py and 2px atomic orbitals from fluorine. The above 3 molecular orbitals are in the HOMO/LUMO region.
H2SiO (Extra)
Molecule: H2SiO
Optimisation
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -365.90001403 au
RMS Gradient: 0.00000941 au
Point Group: CS
Optimised Si-H bond length: 1.48652 angstroms
Optimised Si-O bond length: 1.53172 angstroms
Optimised O-Si-H angle: 124.158 degrees
Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000023 0.001800 YES RMS Displacement 0.000017 0.001200 YES
The Optimised Molecule |
Vibrations
Below is the vibration information for H2SiO
With the 3n-6 rule (n=4), 6 modes are expected. The above set of information shows that there are no degenerate vibrations but some are relatively close in energy.
Charges
Si-atom charge: 1.472
O-atom charge: -1.001
H-atom charge: -0.236
These results are expected as oxygen is more electronegative than silicon and hydrogen so would make silicon slightly positive and, because of this, hydrogen would be slightly negative.
- ↑ V.Chaban, Vitaly; V.Prezhdo, Oleg (June 2016). "Haber Process Made Efficient by Hydroxylated Graphene: Ab Initio Thermochemistry and Reactive Molecular Dynamics". J. Phys. Chem. Lett. 7 (13). DOI: 10.1021/acs.jpclett.6b01178