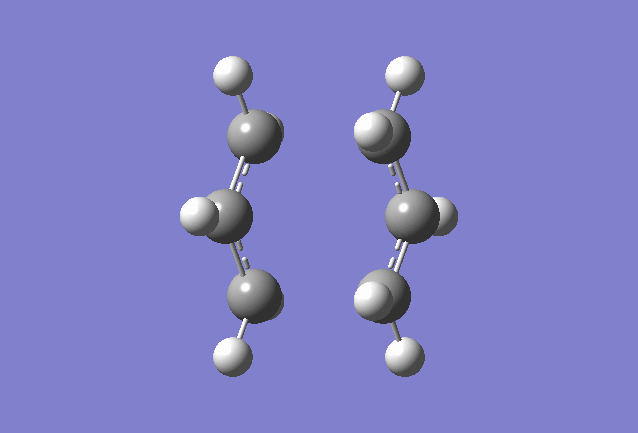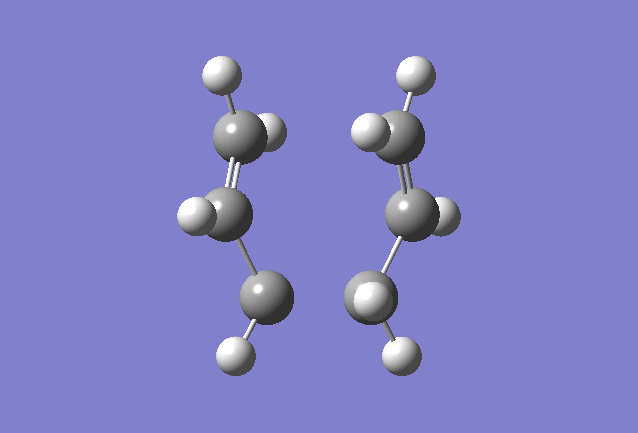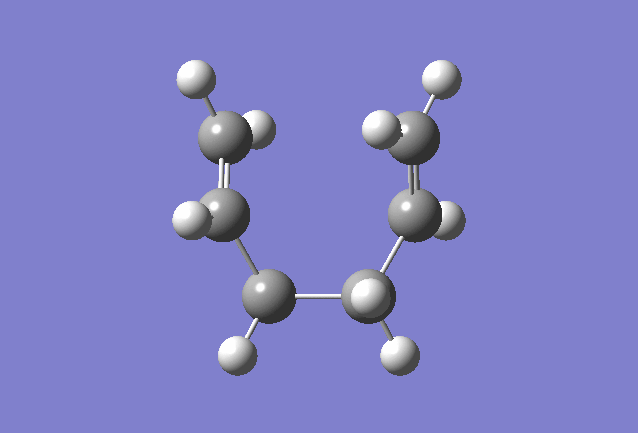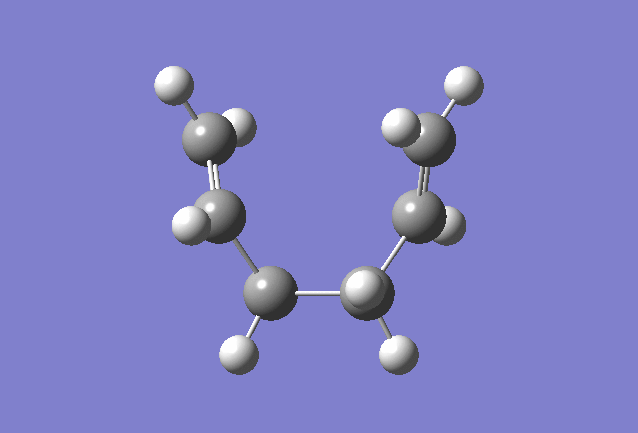Rep:Mod:nht10mod3
This computational laboratory (Modue 3 - Transition states and reactivity.) utilizes Gaussian to study the transition structures of the Cope rearrangement and the Diels Alder cycloaddition reaction.
Cope Rearrangement
Optimizing the products and reactants
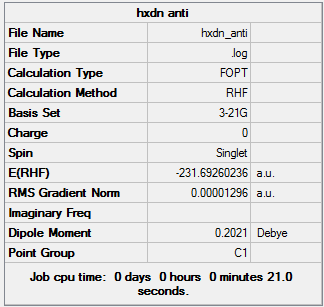
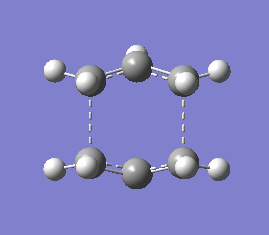
1,5 Hexadiene with "anti" linkage
1,5 Hexadiene with "anti" linkage was first optimized using the 3-21G basis set
1,5 Hexadiene with "anti" linkage |
Summary:
Using the symmetrize option, the point group of 1,5 Hexadiene with "anti" linkage was found to be Ci/C1
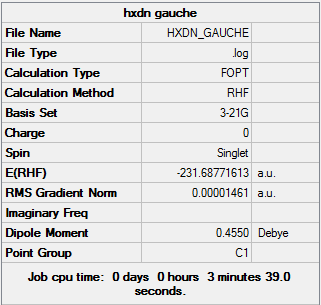
1,5 Hexadiene with "gauche" linkage
1,5 Hexadiene with "gauche" linkage was optimized with the 3-21G basis set
1,5 Hexadiene with "gauche" linkage |
Summary:
1,5 Hexadiene with "gauche" linkage belongs to the C2/C1 point group
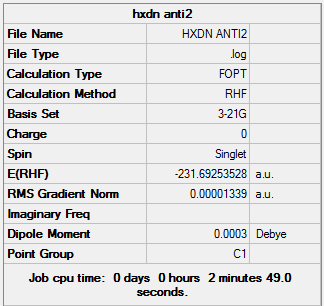
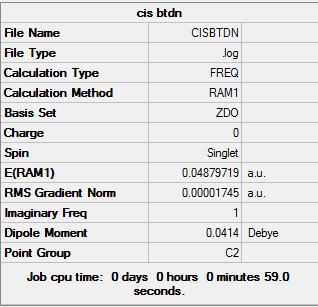
1,5 Hexadiene with Ci anti2 linkage
1,5 Hexadiene with "anti2" linkage was optimized using the 3-21G basis set
1,5 Hexadiene with "anti2" linkage |
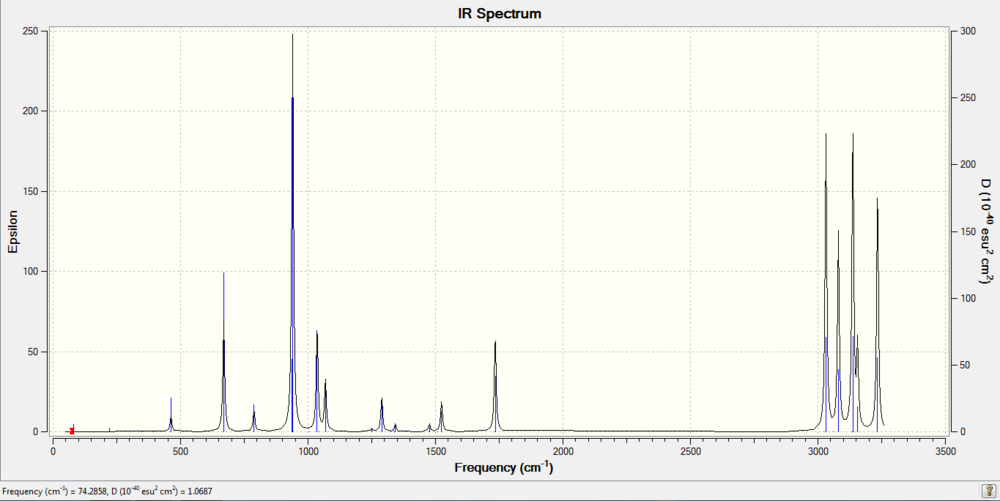
Frequency calculation:
Summary:
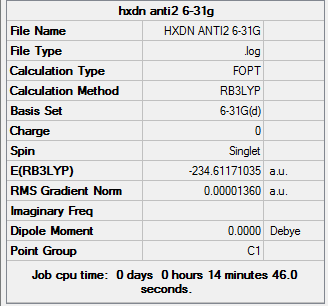
Further Optimisation using the 6-31G basis set
1,5 Hexadiene with "anti2" linkage |
Summary:
A frequency calculation was taken, and this gives the IR spectrum of the molecule
Optimizing the "Chair" and "Boat" Transition" Structures
After optimizing the reactants and products, now the transition states can be computed and optimized.
Optimisation of the Allyl Fragment
To start, the allyl fragment CH2CHCH2 was first optimized using the 3-21G basis set
Allyl Fragment |
Summary:
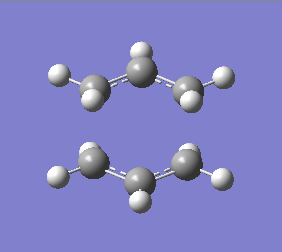
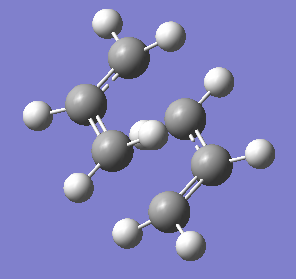
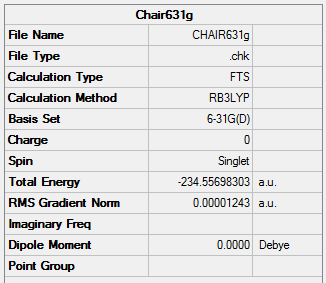
Optimisation of the "Chair" Transition State
The optimized allyl fragment was used to create a chair transition structure, which was then optimised using 2 seperate methods, Method 1 is to compute the force constant matrix (Hessian), Method 2 is to generate the transition structure by freezing the reaction coordinate, and optimize the unfrozen transition state structure once the molecule is fully relaxed.
Method 1
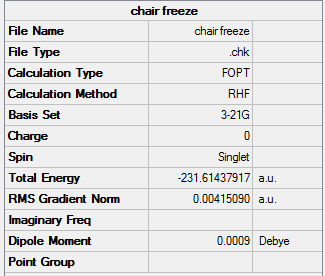
Chair |
Summary:
Transition State:
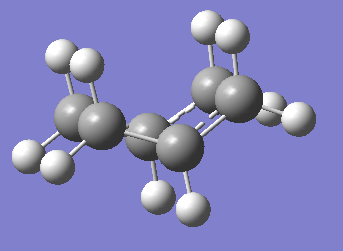
Method 2
Firstly the reaction coordinate was frozen and the molecule was optimized:
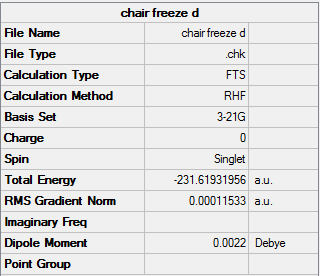
Chair(Frozen Coordinate) |
Summary:
Then the reaction coordinate was unfrozen and optimized:
Chair (Optimised) |
Summary:
Transition State:
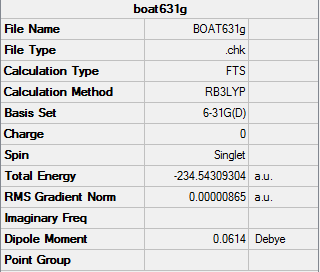
Optimization of the "Boat" Transition State
The "Boat" Transition Structure was optimized using the QST2 method. The previously optimized anti2 1,5 hexadiene molecule was used in this part of the optimisation. The central C-C-C-C dihedral angle and the C2-C3-C4/C3-C4-C5 angle were modified to give a "Boat" like structure, by further optimising using the QST2 calculation, the transition state can be computed.
Boat |
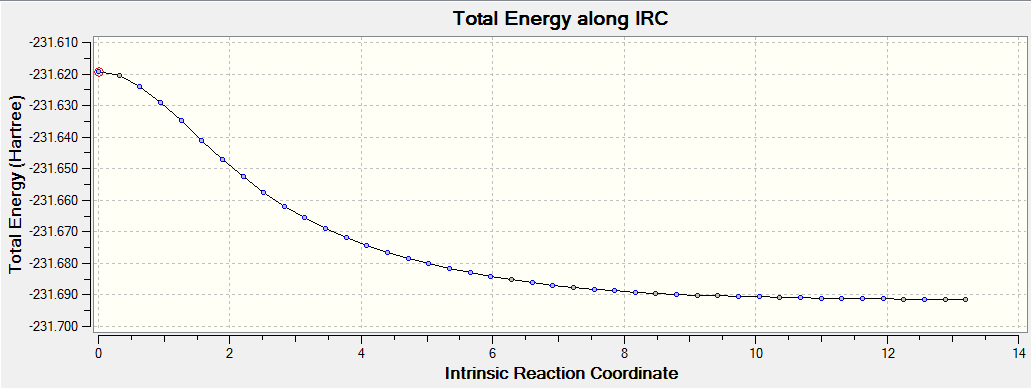
Intrinsic Reaction Coordinate of the "Boat" Transition State
The Intrinsic Reaction Coordinate (IRC) computes the conformer that the transition state will lead to, and it was used on the "Boat" transition state.
The force constants in this calculation was calculated once
Summary:
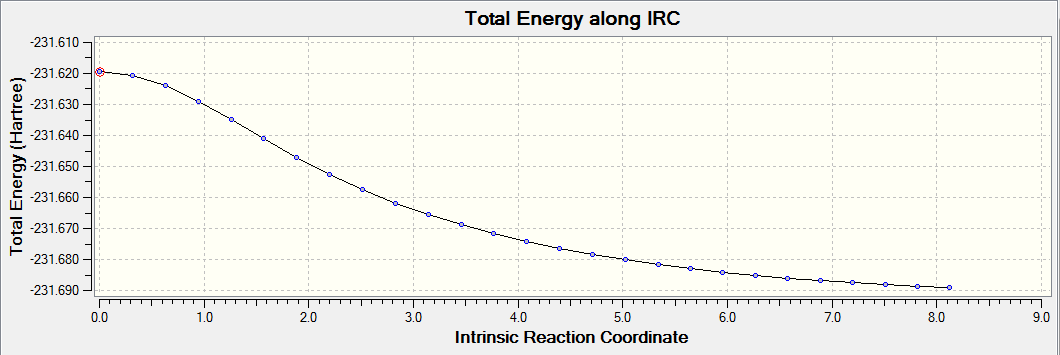
IRC with Force Constant Calculated at Every Step
To determine the minimum geometry, the force constants were calculated at every step to give the following reaction path and final structure
The energy pathway of the reaction after 50 points taken (force constant calculated at every step):
The IRC with force constant calculated at every step has a lower energy minimum than the IRC with force constant calculated only once. Hence it was assumed that the former has the minimum geometry
Further Optimization of the "Chair" and "Boat" Transition States
The chair and boat structures were further optimized at the B3LYP/6-31G* level
Chair Transition State
The chair transition state belongs to the C2h point group
Chair |
Summary:
Frequency calculation:
Boat Transition State
The boat transition state belongs to the C2v point group
Boat |
Summary:
Frequency calculation:
Summarizing the Energies of the Reactants and Transition States
By inspecting the .log output files, the sum of electronic and zero-point energies Eelec+ZPE at 0K, and the sum of electronic and thermal energies Eelec+Ether at 298.15K can be found. Comparing the energies of the "Chair" and "Boat" transition states with the lowest energy conformer of 1,5 hexadiene anti2, the activation energy of the Cope rearrangement can be estimated.
Chair Transition State
| HF/3-21G | HF/3-21G | B3LYP/6-31G(d) | B3LYP/6-31G(d) | |
|---|---|---|---|---|
| Eelec+ZPE (0K) | Eelec+Ether (298.15K) | Eelec+ZPE (0K) | Eelec+Ether (298.15K) | |
| anti2/a.u. | -231.539540 | -231.532566 | -234.469204 | -234.461857 |
| Chair TS/a.u. | -231.466696 | -231.461337 | -234.414929 | -234.409008 |
| Eact/a.u. | 0.072844 | 0.071229 | 0.054275 | 0.052849 |
| Eact/kcal mol-1 | 45.71 | 44.70 | 34.06 | 33.16 |
Boat Transition State
| HF/3-21G | HF/3-21G | B3LYP/6-31G(d) | B3LYP/6-31G(d) | |
|---|---|---|---|---|
| Eelec+ZPE (0K) | Eelec+Ether (298.15K) | Eelec+ZPE (0K) | Eelec+Ether (298.15K) | |
| anti2/a.u. | -231.539540 | -231.532566 | -234.469204 | -234.461857 |
| Boat TS/a.u. | -231.450930 | -231.445302 | -234.402339 | -234.396005 |
| Eact/a.u. | 0.08861 | 0.087264 | 0.066865 | 0.065852 |
| Eact/kcal mol-1 | 55.60 | 54.76 | 41.96 | 41.32 |
Comparing with Experimental Values
Comparing the calculated activation energies with the experimental energies of 33.5 ± 0.5 kcal mol-1 for chair and 44.7 ± 2.0 kcal mol-1 for boat at 0K.[1]
The HF/3-21G theory showed deviation from the experimental values but the more complicated B3LYP/6-31G(d) showed agreement with the experimental values. This suggests the 6-31G(d) basis set gives a better estimation of the actual structure of the molecule.
The Diels Alder Cycloaddition
This exercise looks into the properties of the Diels Alder pericyclic reaction. Same as the Cope rearrangement, the transition state and the reactant was first optimized. Every calculation carried out in this section was computed using the semi-empirical/AM1 theory.
Firstly, the Diels Alder reaction between cis-butadiene and ethene was analysed, and then the reaction between cyclohexa-1,3-diene and maleic anhydride was studied.
Optimization of the Reactants
Cis-butadiene
An Optimization+Frequency calculation was performed on cis-butadiene
Summary:
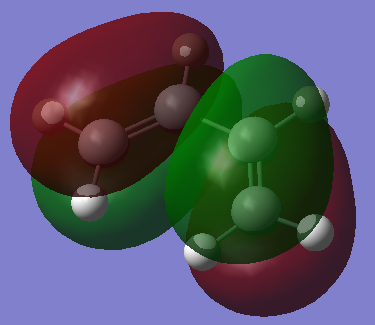
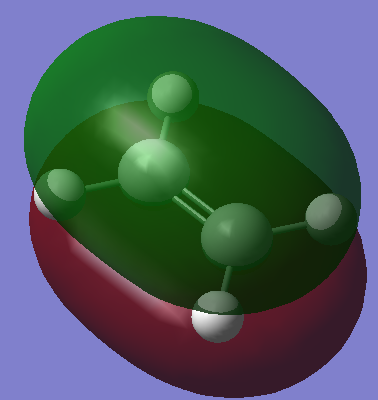
The HOMO and LUMO was also calculated:
HOMO
The HOMO of cis-butadiene is anti symmetric with respect to plane
LUMO
The LUMO of cis-butadiene is symmetric with respect to plane
Ethene
The other reactant ethene was optimized using the same level of theory:
Summary:
HOMO of ethene is symmetric with respect to plane:
LUMO of ethene is anti symmetric with respect to plane:
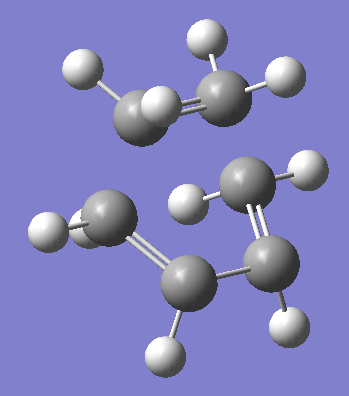
Optimisation of the Transition State
The guess structure of the cycloaddition reaction was obtained from a bicyclo system, having a -CH2CH2- removed and several double bonds added.
Guess structure:
By optimising the guess structure using the keywords
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity
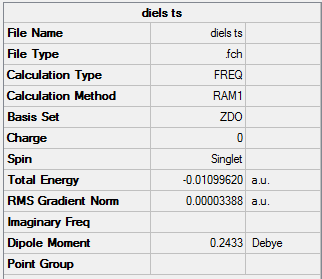
The transition state structure was obtained:
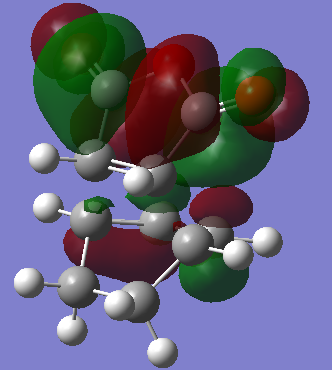
Diels Alder Reaction TS |
Summary:
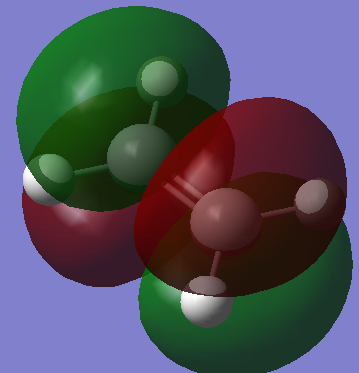
By animating the vibration with negative frequency (-52.69cm-1)in the .chk file, the formation mechanism of 2 bonds can be estimated, in this case the formation of the 2 bonds is happening asynchronously since the vibration is vibrating asymmterically. Comparing the negative frequency to the smallest positive frequency, the smallest frequency is a symmetric vibration (152.31cm-1) with less intensity.
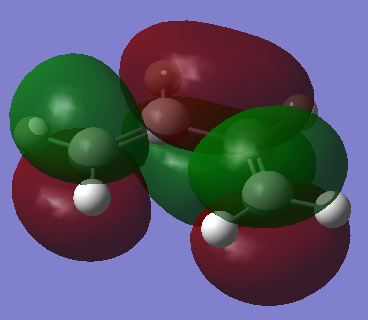
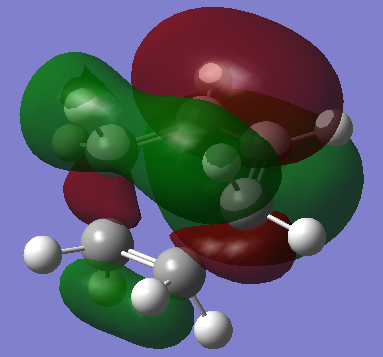
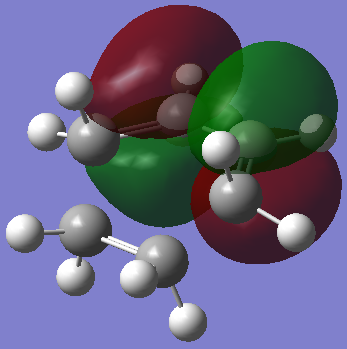
Transition State Molecular Orbitals
HOMO:
The HOMO of the transition state is symmetric with respect to plane
By oberving the HOMO/LUMO of cis-butadiene and ethene, the HOMO of the transition state is assumed to be formed by the ethene HOMO and the cis-butadiene LUMO. This reaction is allowed because HOMO cannot interact with another HOMO, there must be electron transfer (i.e. HOMO donating electron to another molecule's LUMO), and the HOMO can only interact with a LUMO with the same symmetry. In this case, the s (symmetric) HOMO interacts with the s LUMO.
LUMO:
The LUMO of the transition state is anti symmetric with respect to plane
Regioselectivity of the Diels Alder Reaction - Reaction between Cyclohexa-1,3-diene and Maleic Anhydride
Reactant Optimisation
The reactants of the Diels Alder reaction between cyclohexa-1,3-diene and Maleic Anhydride was optimised.
Cyclohexa-1,3-diene
Cyclohexa-1,3-diene |
Maleic Anhydride
Maleic Anhydride |
Transition State Optimisation
By orientating the reactants differently, 2 conformers of the transition state: exo- and endo- can be formed and computed. The transition states were calculated using the freeze coordinate method.
Exo-
The 4 carbons that were involved in the pericyclic reaction was frozen in coordinate on the estimate structure (estimated bond lengths were 1.61Å and 1.60Å respectively), and the rest of the molecule was optimized to a minimum:
Exo- Frozen |
Summary:
Then the molecule was unfrozen and optimized to a TS(berny):
Exo- unfrozen |
Summary:
The resulting bond lengths on the previously frozen carbons are 1.59Å and 1.60Å respectively.
Molecular Orbitals of the Exo- Transition State
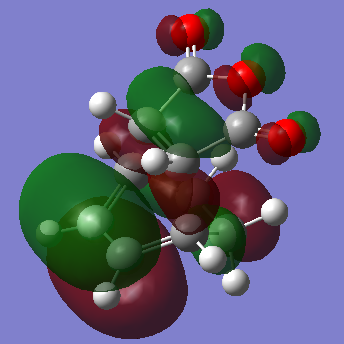
HOMO of the Exo- TS is symmetric with respect to plane
LUMO of the Exo- TS is anti symmetric with respect to plane
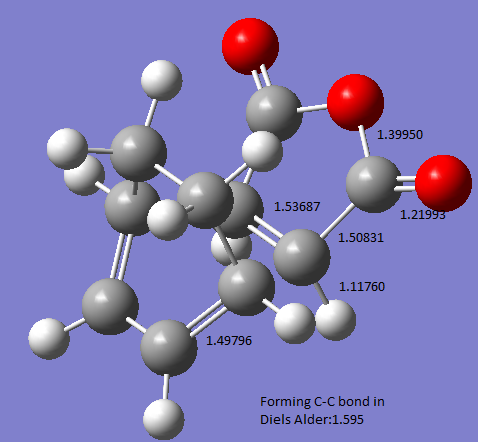
The picture below shows the important bond lengths in the Exo- structure (Å)
Endo-
The same method to the Exo- transition state was used on the Endo- transition state:
Endo- adduct with frozen carbon coordinates (estimate bond lengths being 1.60Å and 1.61Å):
Endo- Frozen |
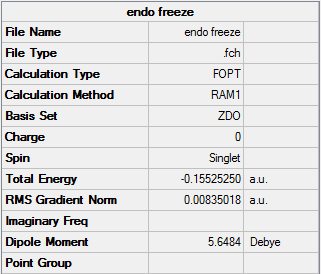
Summary:
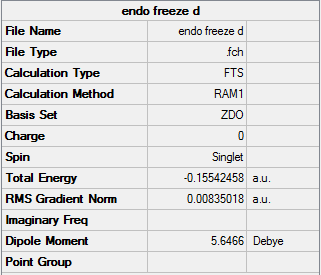
Transition state after unfreezing the carbons:
Endo- unfrozen |
Summary:
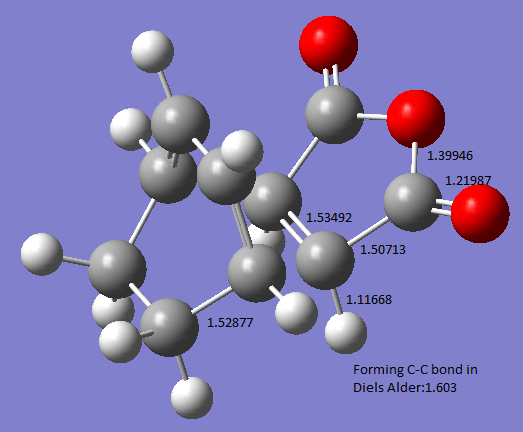
The resulting structure have 1.60Å and 1.61Å in bond length for the 4 previously frozen carbons.
The picture below shows the important bond lengths in the Endo- structure (Å)
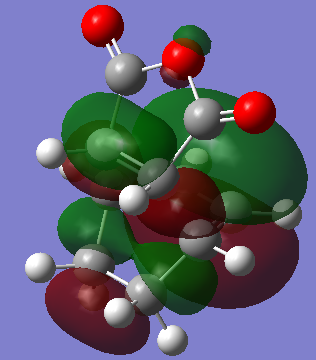
Molecular Orbitals of the Endo- Transition State
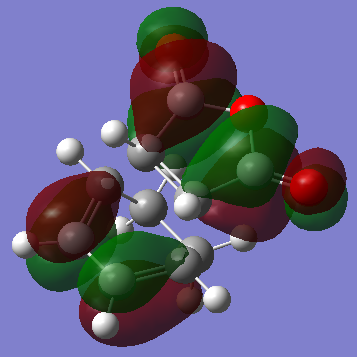
The HOMO of the Endo Transition State is symmetric with respect to plane:
The LUMO of the Endo Transition State is anti symmetric with respect to plane:
Bond Length
A typical sp3 hybridised C-C bond has a bond length of 1.54Å, and a typical sp2 C-C bond length is 1.34Å.[2] The partly formed C-C bond in the transition state has a bond length of around 1.60Å, this indicates that the partly formed C-C has a bond order slightly less than 1.
Comparison between the Exo- and Endo Adduct
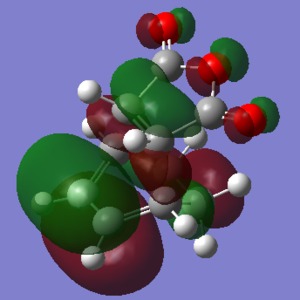
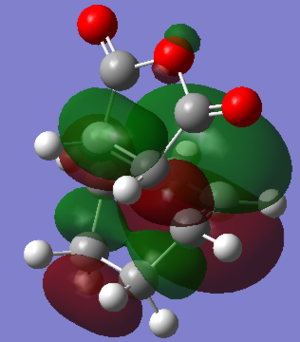
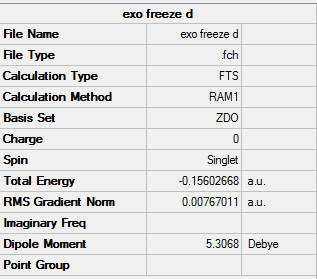
From the calculations that had been done, the Exo- form (-0.15602668a.u.) of the transition state has a lower energy than the Endo- form (-0.15542458a.u.), this is assumed to be due to steric effect, since the Exo- form has the sp3 carbons facing away from the -(C=O)-O-(C=O)- fragment.
Although the Exo- form is lower in electronic energy, the Endo- form is favoured over the Exo- form during the Diels Alder Reaction, this is known to be caused by the effect "secondary orbital overlap effect". If one look at the HOMO of the Endo- TS and Exo- TS, the Endo- TS HOMO has less electron density located on the oxygen atoms on maleic anhydride and has more electron density located on the diene, compared to the Exo- form. This overlap of electron density between the oxygen π system and the dienophile π system stabilizes the overall structure, hence the Endo- form should be having lower energy if considering the π overlapping effect, in these calculation the electronic effect may have not been considered, hence the Exo- form appears lower in energy.[3]
The Endo- form compromises a good balance between the steric effect and the secondary orbital overlap effect, hence the Endo- form is favoured during the cycloaddition reaction.
References
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Results_Table
- ↑ http://ocw.mit.edu/courses/chemistry/5-12-organic-chemistry-i-spring-2003/lecture-handouts/04.pdf
- ↑ Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies, J. Org. Chem., 1987, 52 (8), pp 1469–1474