Module 3 Physical; Experiment 3: The Transition State

Tutorial: The Cope Rearrangement

Optimising the Reactants and Products

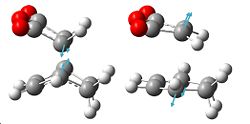
HF/3-21G opt of anti	Showing anti bond	HF/3-21G opt of gauche	showing gauche bond

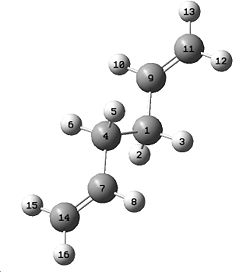
A molecule of 1,5-Hexadiene was created in Gaussview, with an "anti" linkage for the 4 central carbon atoms, by setting the dihedral angle to 180°. The clean function was used on the molecule, followed by a HF/3-21G energy optimisation. This resulted in the molecule shown to the right, with energy -231.69260235a.u.. It initially had no symmetry with C₁ point group, but the symmetrize option was then selected which gave the molecule C₂ symmetry.

Another molecule of 1,5-hexadiene was then drawn in Gaussview with a "gauche" linkage for the 4 central carbons, by making the central dihedral angle 60°, follwed by using the clean function. The HF/3-21G optimisation was then carried out as before, giving the total energy of this conformation to be -231.69153034a.u. Using the symmetrize options again, we obtained a symmetry of C₂.

These two calculations suggest that the anti-conformation is the most stable of the two as it has the lowest total energy. This can be explained by thinking about steric hindrance of the two C=C groups which are brought closer together in the gauche conformation and thus these two groups cause strain in the molecule, increasing the energy. In the anti-, the groups are as far away from each other as possible, lowering the energy of the molecule. However, it has actually been suggested that the gauche conformation should be the lowest in energy due to the fact that in the gauche orientation, the C=C bond is able to eclipse the C-H bond of the methylene group. ^[1] This favourable overlap decreases the energy of the molecule, making the gauche the more energeitcally stable.

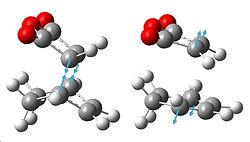
Gauche re-try HF/3-21G optimisation	showing gauche bond

Therefore, it has been decided to try and investigate whether a lower energy gauche conformation is possible, to agree with the C=C / C-H overlap theory. The molecule shown below was created in Gaussview, the geometry cleaned, and the HF/3-21G optimisation carried out. It did give a lower energy of -231.69166702a.u., and again symmetry C₂ after "symmetrize", but this is still not lower than the anti- conformation already found.

The sturctures obtained and their energies were compared to those provided in Appendix 1 Mod:phys3. It can be seen that the anti conformation that was made above was ANTI 1, with a relative energy to the lowest possible conformation of 1,5-hexadiene being 0.04kcal/mol, which is pretty close. The first gauche conformation above was found to be GAUCHE 4, which had a relative energy of 0.71kcal/mol, and the previous gauche was found to be GAUCHE 2, which is closer to the lowest possible conformation with a relative energy of 0.62kcal/mol. However this is still not the lowest energy conformation which is GAUCHE 3 shown in the appendix table. On comparison of the energies obtained and those in the table, it has been shown that the calculations were accurate.

Anti2 HF/3-21G optimisation	showing anti bond

The C_i ANTI2 conformation of 1,5-hexadiene was then created in Gaussview and a HF/3-21G optimisation carried out once the molecule had been "cleaned", which gave a total energy of -231.69253511a.u. and symmetry C_i, which agrees with the data in the appendix table. This was then re-optimised using the B3-LYP/6-31G(d) optimisation, which gave an energy of -234.61172185a.u., which is lower energy than the previous calculation. In order to compare the geometries obtained from these two optimisations we can look at the bond lengths and angles.

bond or angle	HF/3-21G	B3LYP/6-31G(d)
C=C	1.31617Å	1.33451Å
C₄-C₇ (& C₉-C₁ )	1.50882Å	1.50408Å
C₁-C₄	1.55315Å	1.54814Å
Central dihedral C-C-C-C	-114.653°	-118.490°
C₁₄-C₇-C₄	124.801°	125.297°

This has shown that the B3LYP-6-31G(d) method has made the C=C double bond shorter and the C-C bonds longer in comparison to the HF/3-21G method. This may have reduced the energy of the conformation, as it has made the two side groups including the smaller C=C bond spacially further away from each other, reducing the degree of steric hindrance and thus reducing the energy of the molecule. We can also see that the B3-LYP/6.31G(d) has made the dihedral angle larger and thus made the two groups further away from each other, whilst still keeping the C=C to C-H overlap.

An IR frequency was then carried out on the B3LYP/6-31G(d) resulting in the following IR, with no imaginary frequencies:

Using the output file under the section thermochemistry the following was obtained:

Sum of electronic and zero-point Energies=           -234.469182
Sum of electronic and thermal Energies=              -234.461844
Sum of electronic and thermal Enthalpies=            -234.460900
Sum of electronic and thermal Free Energies=         -234.500730

Sum	Explanation
i) electronic and zero-point energies	E at 0K inc. 0 point vib E (E = Eelec + ZPE)
ii) electronic and thermal energies	E at 298.15K and 1atm inc translational, rotational and vibrational energy modes (E = E + Evib + Erot + Etrans)
iii) electronic and thermal enthalpies	additional correction for RT (H = E + RT)
iv) electronic and thermal free energies	entropic contribution to the free energy (G = H - TS)

Optimizing the "Chair" and "Boat" Transition Structures

Chair

An allyl fragment (CH₂CHCH₂) was drawn in Gaussview and optimised using the HF/3-21G optimisation. This is shown to the left, with an optimised total energy of -115.823a.u.

This fragment was then copied and pasted into a new window twice, and the two allyl fragments were orientated so that they looked like a chair transition state (shown below). The distances between the two terminal carbons on each allyl fragment were set to 2.2Å using Gaussview. This "guess" of the transition state was then copied into a new window, and a new optimisation and frequency calculation of this transition state was carried out. The optimisation was HF/3-21G set to a TS(Berny), the force contants were to be calculated once, and Opt=NoEigen was added to the Additional keyword box at the bottom. This gave the following script:

    # opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity

"Guess" of Chair TS (bond = 2.2Å)	TS after optimisation (bond = 2.024Å)	Vibration at Imaginary Frequency after TS Optimisation

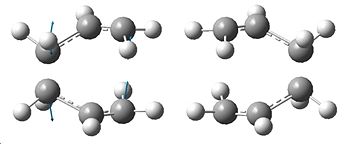
The optimised TS can be seen to the right, with a total energy of -231.61932232a.u. and symmetry C_2h. The frequency calculation gave one imaginary frequency at -818.127cm^-1, the vibration of which corresponds to the Cope rearrangement, and is shown. We can see that the optimisation has decreased the distance between the two terminal carbons on the allyl fragments.

The "guess" structure was once again taken and pasted into a new window. The Redundant Coord Editor was selected and the highlighted file icon selected to create a new coordinate. The two terminal carbons were selected followed by selecting bond then freeze coordinate in the redundant coord editor box. The bond lengths were set to 2.2Å. This was repeated with the other two terminal carbons which form/break a bond during the rearrangement. A minimum optimisation was then carried out using the script shown:

  # opt=modredundant hf/3-21g geom=connectivity

This resulted in a structure similar to that previously, but the bond lengths between the terminal carbons were exactly 2.2Å, and the energy was -231.61518538a.u..

The Redundant Coord Editor was opened again, and this time the bonds were set to bond and derivative. From this, a TS HF/3-21G optimisation was carried out, but this time not calculating the force constants. The script is shown below:

  # opt=(ts,modredundant,noeigen) rhf/3-21g geom=connectivity

NoEigen was included to ensure there was only one imaginary frequency, and Gaussview seemed to crash when this was not included. The results of this optimisation can be shown below. The energy was calculated to be -231.61932239a.u. and the distances between the terminal carbons are 2.02074Å and 2.02069Å. These are shorter distances when comparing to the previous TS optimisation above, which had lengths of 2.02412Å. Also, we now have the exisitance of 2 different distances between the two sets of terminal carbons, which had not been observed before. This shows bias toawrds the shorter distance being the one that forms a bond, and the longer is the one which has broken.

Final optimised Chair Transition state

Boat

Reactant

Product

The boat transition state was then investigated, with the structure to be optimised using the QST2 method, which allows us to specify the reactants and products for thr reaction. However, to ensure this works correctly, the atom numbers must match up (i.e. atoms numbers must stay the same between the reactant the the rearranged product), and so the atom labels had to be altered to those shown to the left. This was done by opening up the previous optimised .chk file fo the ANTI2 molecule, and copying it to a new window. Then, this was added to the window again using Add to MolGroup which gave two of the same molecule, the reactant and product, allowing us to see them simultaneously in the Gaussview window. The atom labels were then changed to correspond with the cope rearrangement (shown right).

Failed Boat TS

Using these newly labelled molecules, a TS (QST2) HF/3-21G Optimisation and Frequency was carried out using the following script:

  # opt=qst2 freq hf/3-21g geom=connectivity

This job failed, giving the error message "Severe Error Message #2070 - The Processing of the last link ended abnormally. All processing has been aborted". The .chk file was opened which showed the structure shown to the right, which is obvously wrong, as it has become more like the chair TS, showing it to be impossible to generate the boat TS from this initial structure.

Therefore, to improve this and gain the boat TS we have to modify the starting structures so that they are closer to the boat transition state. This was done first on the reactant molecule by making the central dihedral angle 0°, and the inside angles (C2-C3-C4 and C3-C4-C5) 100°. This was then repeated on the product molecule, giving the structures shown below:

Reactant

Product

The QST2 calculation was set up again, which resulted in the boat TS structure shown below. There was also one imaginary frequency at -839.167cm^-1, which is also shown. The C-C distance was found to be 2.13974Å for both terminal pairs of carbons, and it has symmetry C_2V

TS after optimisation	Vibration at Imaginary Frequency after TS Optimisation

It is not possible to determine which conformer the transition states have come from. To do this we have to use the Intrinsic Reaction Coordinate (IRC) Method, as this allows us to follow the minimum energy path from the TS down to its minimum energy. i.e. the starting conformation.

The .chk file for the optimised chair TS was opened and copied into a new window. A Guassian calculation was started, selecting IRC and choosing to compute the reaction coordinate in just the forward direction due to our molecule being symmetrical. The force constant was also chosen to be calculated only once, and the number of points changed to 50. This gave the following command:

 # irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity

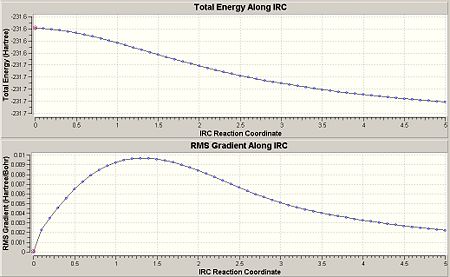
This gave the following results shown as the graph below, including the 1st, 30th and 51st geometries of the molecule to show the change as the IRC calculation progresses. The min energy here was given to be -231.68041689a.u.

IRC Graph	Step 1	Step 30	Step 51

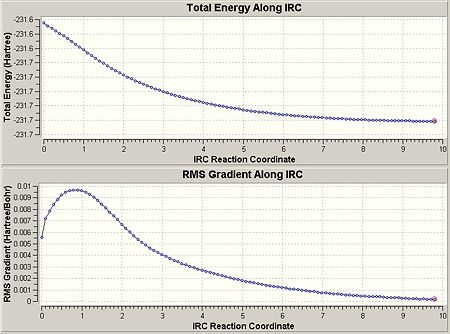
As we can see, it has not reached the minimum energy yet, so this was repeated using 100 steps, as this larger number of points allowed it to reach the minimum, shown by the graph below. This gave a final energy as -231.69074482 and symmetry C₂:

IRC Graph	Step 1	Step 101

The mininum energy geometry from the first IRC calculation was also taken and a normal minimum optimisation carried out, giving the same geomety as shown above, but a lower energy of -231.69166702a.u. and symmetry C₂.

There was not sufficient time to carry out the 3rd option which was to calculate the force constant at each step.

From carrying out this IRC method we have been able to distinguish which is the most likely conformation that the chair is derived from, which we can conclude to be the GAUCHE 2 conformer, due to it being close in energy and of the same symmetry and geometry.

Activation Energies

B3-LYP/6-31G optimisations and frequency calculations were carried out on the chair and boat transition structures, using the previously optimised HF/3-21G structures. comparing these to the previous reactant molecules we can find the activation energy:

Chair TS B3-LYP/6-31G

Sum of electronic and zero-point Energies=           -234.414920
Sum of electronic and thermal Energies=              -234.409001
Sum of electronic and thermal Enthalpies=            -234.408057
Sum of electronic and thermal Free Energies=         -234.443803

	HF/3-21G optimisation energy (Hartree)	B3-LYP/6-31G optimisation energy (Hartree)
C_i ANTI 2	-231.69253511	-234.61172185
Chair TS	-231.61932239	-234.55698273
Boat TS	-231.60280143	-234.54309295

Boat TS B3-LYP/6-31G

Sum of electronic and zero-point Energies=           -234.402342
Sum of electronic and thermal Energies=              -234.396005
Sum of electronic and thermal Enthalpies=            -234.395061
Sum of electronic and thermal Free Energies=         -234.431100

As we can see above, the HF/3-21G method has calculated all 3 energies to be higher and less energetically stable than the B3-LYP/6-31G calculation, and this difference of approximately 3 Hartree is relatively large. This is quite surprising that the magnitude of the difference is this large, due to the geometries of the molecules stay pretty much the same. For example the distance between the terminal carbons in the chair conformation is 2.02069Å for the HF/3-21G, and for the B3-LYP/6-31G(d) it has only changed slightly to a length of 1.96588Å. This allows us to conclude that it is best to do a low level calculation first to generate the optimised structure of the molecule, but a higher level calculation such as B3-LYP/6-31G(d) is required to gain an accurate energy.

Knowing the thermochemical data for both the reactant and both the TS for the B3-LYP/6-31G optimisation it is possible to calculate the Activation Energy for both the chair and boat conformations at 0K. This is found by taking away the energy of the sum of the electronic and zero point energy for the reactant away from that of the transition state:

A_E for Chair TS = (-234.414920) - (-234.469182) = 0.054262 Hartree = 34.0499264 kcal/mol

A_E for Boat TS = (-234.402342) - (-234.469182) = 0.06684 Hartree = 41.9427422 kcal/mol

The experimental activation energies were found to be 33.5 ± 0.5 kcal/mol for going via the chair TS, and 44.7 ± 2.0 kcal/mol for the boat, at 0K. This shows that both of the calculated activation energies are relatively close to those experimentally, and that the chair ts state is the lowest energy transition state. This can also be calculated for 298.15K using the Sum of electronic and thermal Enthalpies sum:

A_E for Chair TS = (-234.408057) - (-234.460900) = 0.052843 Hartree = 33.15949022 kcal/mol

A_E for Boat TS = (-234.395061) - (-234.460900) = 0.065839 Hartree = 41.31460508 kcal/mol

The Diels Alder Cycloaddition

The next part of this project involves looking at the Diels Alder cycloaddition of ethylene and cis-butadiene, followed by the regioselective Diels Alder of cyclohexa-1,3-diene and maleic anhydride.

Ethylene and cis-Butadiene

The reaction of ethylene and cis-butadiene is a [4s+2s] cycloaddition reaction, shown to the right, involving both the HOMO and LUMO orbitals of both molecules (where the HOMO & LUMO of ethlyene is the π & п* orbitals). It is an allowed reaction due to it being a (4n+2) thermal process. We can start by looking at the molecular orbitals of both reactants.

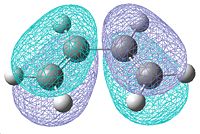
A molecule of cis-butadiene was drawn in Gaussview and optimised using the AM1 semi-empirical molecular orbital method. This allowed us to visualise the molecular orbitals, as shown below:

Optimised cis-Butadiene molecule	HOMO	LUMO

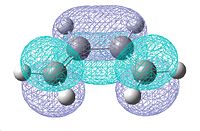
Drawn MOs with plane of symmetry
Symmetry with respect to plane	Anti-symmetric (a)	Symmetric (s)

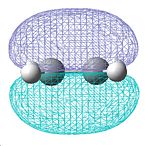
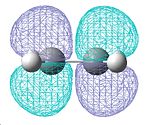
A molecule of ethylene was then created and optimised in Gaussview, allowing us to see its HOMO and LUMO(π & п* orbitals), and again determine their symmetry:

Optimised ethylene molecule	HOMO	LUMO

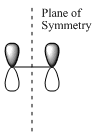
Drawn MOs with plane of symmetry
Symmetry with respect to plane	Symmetric (s)	Anti-symmetric (a)

The next step was to then create the transition state which has an envelope type structure which allows optimum overlap of the orbitals. This was carried out by drawing a bicyclo system and removing the -CH₂CH₂- as suggested, and making sure there was the correct number of hydrigens present on the molecule. This was known as the "guess" structure. From here, the "bond forming" C-C bonds were lengthened to 2.2Å, as this length has worked well previously. The structure was then optimised using the AM1 semi-empirical optimisation and the "freeze bond" then "derivative bond" method. The bonds were first frozen to 2.2Å using the Redundant Coord editor, and the optimisation carried out using the following script:

 # opt=modredundant freq am1 geom=connectivity

From this optimisation, the redundant Coord Editor was re-opened and this time the "bond forming" C-C lengths were selected and changed to "bond - derivative". A TS optimisation with AM1 simi-empirical was carried out including the Opt=NoEigen in the Additional Keywords box:

 # opt=(ts,modredundant,noeigen) freq ram1 geom=connectivity

This gave the structure shown below with an energy of 0.11162916a.u. and symmetry C₁ It also had an imaginary frequency at -956.367cm^-1 which corresponds to the transition state, and shows sinchronous formation of the two bonds. Looking at the first positive frequency vibtration at 146.872cm^-1, we can see no relation to the transition state formation, as none of the vibrations show the forming of a bond between the terminal carbonds. Instead all wee see is an asymmetric orck of the ethylene over the butadiene.

Guess TS structure	Structure after Freeze Opt	Final TS Structure	Imaginary Freqency Vibration

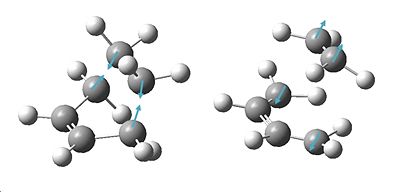
In the final TS structure there is a C-C bond distance of the partly formed δ bond of 2.11888/2.11894 Å. This can be compared to normal sp³C-C, sp² C-C and the Van der Waals radii for C:

sp³C-C: 154pm = 1.54Å website
sp²C-C: 134pm = 1.34Å website
Van der Waals Radii C: 170pm = 1.7Å ^[2]

As we can see, the C-C bond distance of the partly formed δ bond is longer than both a C-C sngle and double done, suggesting that there is no bond yet. However, this distance is shorter than 2 of the Van der Waals radii (3.4Å) showing that there is an attraction between the two atoms, and they are being brought close together; there is just not sufficient bonding yet.

Using this optimised transition state structure, we were able to visulise the HOMO & LUMO molecular orbitals:

HOMO	LUMO

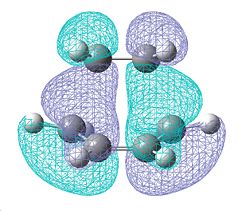Symmetry = Anti-symmetric (a)	Symmetry = Symmetric (s)
Created from HOMO of Butadiene and LUMO of ethylene	Created from LUMO of Butadiene and HOMO of ethylene

As previously said, it is an allowed reaction due to it being a (4n+2) thermal process. We can see this in the molecular orbitals as the HOMO of the butadiene can interact with the LUMO of the ethylene and are in phase with each toher, giving constructive suprafacial overlap. Thus the reaction is allowed.

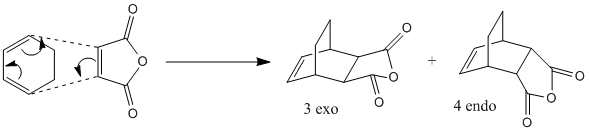
Cyclohexa-1,3-diene and Maleic Anhydride

The above reaction involves the Diels Alder [4πs+2πs] cycloaddition of cyclohexa-1,3-diene and maleic anhydride. The endo product is the major adduct of the kinetically controlled reaction, showing that the exo transition state is higher in energy i.e. has less stabilisation. This was investigated by creating the transition states of both the endo and exo conformations and investigating their energies.

The endo transition state was first made in gaussview, by orientating the C=O-O-C=O of the maleic anhydride over the C=C double bond of the cyclohexa-1,3-dinene. The bond forming C-C distances were then set to 2.2Å. The "freeze bond" method was then chosen for the optimisation, setting the bond first to 2.2Å, and optimising using the AM1 semi-empirical method, shown with the script below. Following this, the bond labelling was changed to "bond - derivative" and a TS optimisation carried out, using the second script shown:

# opt=modredundant freq am1

# opt=(ts,modredundant,noeigen) freq ram1 geom=connectivity

This method was then repeated again for the exo adduct, but this time the "guess" of the transition state structure had the C=O-O-C=O of the maleic anhydride over the C-C single bond of the cyclohexa-1,3-dinene. This gave the following two exo and endo TS structures shown below:

Adduct

Geometry

Energy

Imaginary
Frequency (cm^-1)

Vibration of Imaginary Frequency

C-C forming bond
distance

Endo

Pentahelicene

-0.05159430a.u.

-805.631

2.16245/2.16238Å

Exo

Pentahelicene

-0.05050320a.u.

-811.333

2.17036/2.17050Å

As shown, we can conclude that at this level of calculation, the endo TS has the lower energy, and thus that is why it is the major product under the kinetically controlled reaction. It has also been shown by observation of the imaginary frequencies that it has synchronous bond forming for both the exo and endo, but the endo imaginary frequency is at a lower energy. Lastly, we can see that the bond forming C-C distance on the endo is slightly shorter than that on the exo, showing it to be preferring to form a bond with this conformation.

Other bond lengths and distances of the exo and endo can be seen below:

Endo

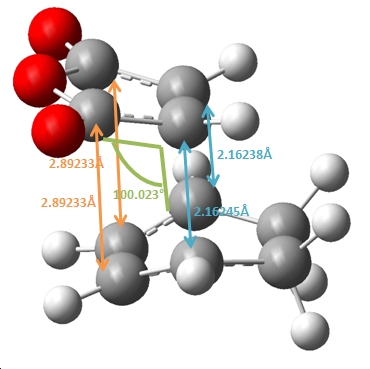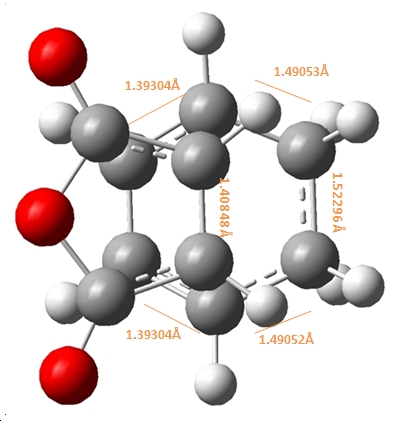
Exo

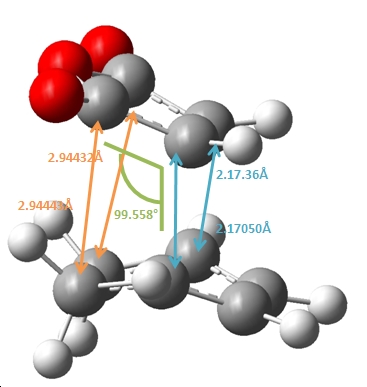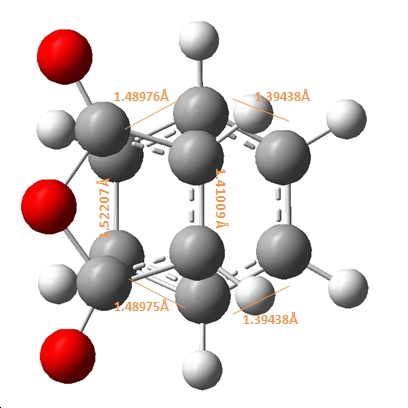
As shown above, the endo product shows the partly formed σ C-C bonds to be ~2.16Å, in comparison to the exo σ C-C bonds which has a longer 2.17Å distance. This suggests that the endo formation has a stonger C-C interaction and partial bond in the transition state. This can be attributed to the steric repulsions through space between the C=O-CO-C=O- of maleic anhydirde and the “opposite” -CH2-CH2- on the ring for the exo, as the additional H atoms on the exo compared to the endo at this point (which has a corresponding -CH=CH- ) effictively push the maleic anhydride ring away making this through space distance 2.944Å for the exo, in comparison to 2.892Å for the endo.

website

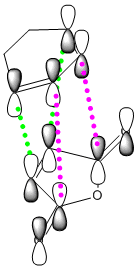
We can also account for the shorter σ C-C partially formed bonds of the endo by taking into account the addiitional secondary orbital overlap interaction. As shown in the diagram of the HOMO of the diene (cyclohexa-1,3-diene) and the LUMO of the dienophile, the endo conformation allows both the formation of the σ C-C bond, shown here in green, but also an additional non-bonding but still favourable secondary orbital overlap shown in pink. Due to the approach of the exo conformation for the TS, this secondary orbital overlap does not occur, and thus is less favoured.

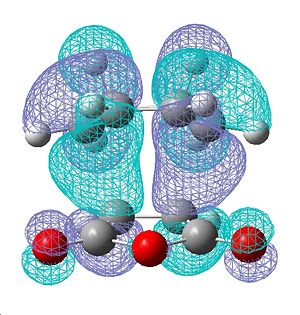
Endo HOMO	Exo HOMO

Above we can see the HOMO for both the endo and exo transition states. Interestingly, whilst we can see obvious lobes for showing electron density being around the area formign the σ C-C bond, for both the endo and exo, we see a lack of electron density and lobes in the area between the -C=O-CO-C=O- of the maleic anhydride and the -CH=CH-, suggesting a lack of secondary orbital interaction. However, interations present in other MOs of this transition state may have some suggestion of secondary orbital overlap, accounting for the additional stabilisation of the endo.

References

↑ Journal of Molecular Structure; Vol 346, 1995;63-69 DOI:10.1016/0022-2860(94)09007-C
↑ J. Phys. Chem., 1964, 68 (3), 441-451 DOI:10.1021/j100785a001

[gauche-1] Journal of Molecular Structure; Vol 346, 1995;63-69 DOI:10.1016/0022-2860(94)09007-C

[2] J. Phys. Chem., 1964, 68 (3), 441-451 DOI:10.1021/j100785a001

[1]

[2]