Rep:Mod:nads878

The Basic Techniques of Molecular Mechanics and Semi-Empirical Molecular Orbital Methods for Structural and Spectroscopic Evaluations

The Hydrogenation of the Cyclopentadiene Dimer

The following molecules were made using ChemBio3D and the conformations optimised using the MM2 optimisation:

Exo	Endo	Dihydro derivative (no.3)	Dihydro derivative (no.4)	Fully Hydrogenated
Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene

Comparing Exo with Endo

	Exo	Endo
Stretch:	1.2923	1.2454
Bend:	20.5870	20.8603
Stretch-Bend:	-0.8413	-0.8320
Torsion:	7.6715	9.5039
Non-1,4 VDW:	-1.4358	-1.5083
1,4 VDW:	4.2320	4.3012
Dipole/Dipole:	0.3778	0.4448
Total Energy:	31.8834 kcal/mol	34.0153 kcal/mol

The cyclopentadiene dimer is formed by a diels-alder (4+2)-cycloaddition reaction. There are two possible structures of the dimer, the endo and the exo. Calculating the energy of the 2, it has been shown that the exo form of the dimer has the lowest energy conformation, 31.8834mcal/mol, in comparison to the endo with energy 34.0153kcal/mol. An explanation for this lower energy is seen when looking at the energy values obtained (above left) for the torsion from the calculation. The exo dimer has a much lower value than the endo, 7.6715kcal/mol versus 9.5039kcal/mol respectively. This is due to the closer proximity of the 2 rings in the endo form than the rings in the exo. The exo dimer is the more energetically stable, and thus would be the thermodynamic product of the reaction.

However, it is known that the endo dimer is the major product of the dimerisation, which shows that it is not the Thermodynamic product that is formed, but the Kinetic. This is experimentally proven when the dimerisation can occur at room temperature overnight.

Endo attack	Exo Attack

Comparing Hydrogenation products

	No. 3	No.4
Stretch:	1.2324	1.0963
Bend:	18.8641	14.5074
Stretch-Bend:	-0.7625	-0.5493
Torsion:	12.2469	12.4972
Non-1,4 VDW:	-1.5627	-1.0507
1,4 VDW:	5.7523	4.5124
Dipole/Dipole:	0.1631	0.1407
Total Energy:	35.9337 kcal/mol	31.1540 kcal/mol

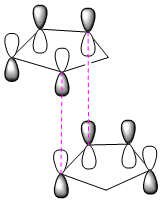
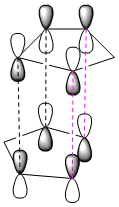
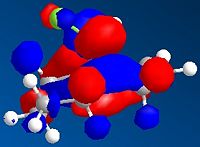
The production of the endo dimer can be explained by looking at the frontier orbitals (HOMO & LUMO) for cyclopentadiene. When the two rings approach each other they can either approach via endo attack, or exo attack. As we can see in the diagrams below, during endo attack the HOMO and LUMO of the two rings have favourable overlap due to the correct symmetry of all the 4 orbitals. Thus, we gain primary orbital overlap from 2 pars of orbitals (pink dotted line), forming 2 new δ bonds, along with 2 other pairs of orbitals which have enough favourable interaction across the space to give the dimer its endo shape (secondary orbtal overlap).

From looking at the exo dimer, the exo approach only allows for the interaction of the 2 pairs of bonding orbitals, and is thus less favoured kinetically. The orbital interaction from the endo attack gives the endo product a lower energy of formation (Activation Energy), which is why it is the major product of the kinetically controlled reaction.

When looking at the products of hydrogenation, we can see that the No.3 product has the highest total energy, 35.9337kcal/mol, compared to the lower energy No.4 product which has just 31.1540kcal/mol. No.4 has a lower stretch and bend energy, which is due to the position of the double bond in the molecule. The Torsion and Van der Waals (VDW) for both are relatively similar. However, this lower total energy for no.4 shows that this conformation would be the thermodynamic product of the hydrogenation.

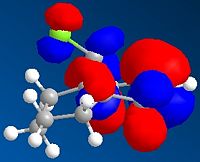
Stereochemistry of Nucleophilic Addition to a Pyridinium Ring (NAD⁺ analogue)

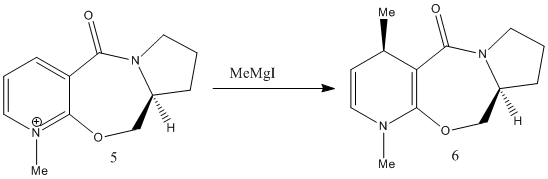
This first reaction involves the reaction of a pyridinium ring compound, no.5,with the Grignard Reagent, to give the product no.6. In the ChemBio3D programme it was not possible to include the MgI in the calculations of the energy of the molecule no.6 as it came up with the error "No atom type was assigned to the selected atom" due to the presence of the Mg in the formula.

The structures of both the reactant and product can be seen below.

No.5	No.6
Pentahelicene	Pentahelicene

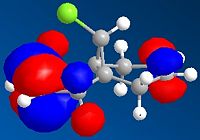
Molecule no.5 was found to have a total energy of 26.3085kcal/mol. The origin of this energy is mainly from the bend energy of 11.3321kcal/mol and the 1,4-Van der Waals energy of 11.9kcal/mol. If we look at the molecule from the perspective of the aromatic ring to the left side, we can see that the oxygen is coming out of the plane, with a dihedral angle of 21.4°.It was tried on ChemBio3D to change the dihedral angle of the oxygen, but all other conformations proved to be higher energies. For example, oxygen into the plane, at a dihedral angle of -119.1° gave an energy of 157.5241kcal/mol, which is significantly higher. This is majorly due to the 166.7238kcal/mol bend energy created by moving the oxygen.

The orientation of the C=O group with respect to the aromitic ring is seen to not change during the reaction. This is because the Grignard, MeMgI, can co-ordinate to the amide oxygen atom, forming a 6 membered ring transition state. Thus, the Me is attached to the same face of the molecule as the oxygen atom, allowing it to say in the same orientation.

The magnitude of the dihedral angle, however, decreases in the product (no.6) to a dihedral angle of 10.9°. This decrease is due to the introduction of the Me group which is also orientated out of the plane, and thus would interact with the oxygen atom, causing it to move in slightly. The product is also higher energy, 28.8745kcal/mol, compared to the reactant, and this is again mainly contributed by the 1,4-VDW and bending energies.

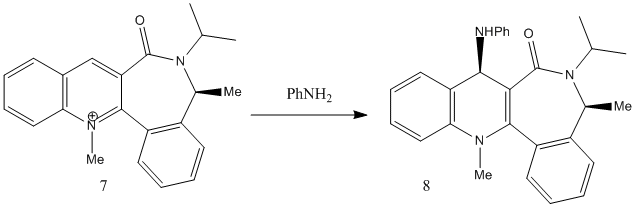
The next reaction can be seen below, involving an axially chiral quinolium salt, no.7, reacting with aniline to give no.8, known as an "amide transferring agent". :

Reaction	No.7
	Pentahelicene

MM2 optimisation of no.7 gave a total energy of 15.2340kcal/mol and a dihedral angle with the oxygen of -43.3°. This shows the oxygen to be out of the plane in the opposite direction than that on molecule no.5. It was tried to move to position of the oxygen, but all other conformations were of significantly higher energy e.g. dihedral angle of -126.2° had a total energy of 144.3651kcal/mol, which was mainly due to the high bending energy of 111.8386kcal/mol.

Unlike the previous reaction, the aniline attacks the molecule on the opposite face to the oxygen, and attaches to the top face. This is due to the fact that the oxygen is not involved in the reaction i.e. not in the transition state, and so it is most likely the repulsion between the lone pairs of the oxygen and the lone pairs on the N of aniline that repel each other sufficiently to hinder the attack of the aniline on the same face of the oxygen.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

No.10	No.11
Pentahelicene	Pentahelicene

The 2 molecules shown below and to the right are a key intermediate in the synthesis of Taxol. They are known as atropisomers, due to the fact that the energy of bond rotation is so high due to hindrance, that 2 isolated conformers can exist. In this case, the carbonyl oxygen can point up (no.10) or point down (no.11)

no.10 no.10 no.11 no.11

The energies were calculated using the MM2 optimisation and were found to be 52.5861kcal/mol and 44.9883kcal/mol for no.10 and 11 respectively, showing no.11 with the carbonyl pointing down to be the most energetically stable isomer, with lower torsion and stretch energies.

The alkene will react slowly due to the fact that the atropisomers are known as hyperstable alkenes. Generally, it is said that a cycloalkane is more energetically stable than the corresponding cycloalkene, as the strain energy of the cycloalkene is higher. The cycloalkene therefore has a positive Olefin Strain Energy. In the case of hyperstable alkenes, the Olefin Strain Energy is a negative value, showing that hydrogenation to the alkane is unfavoured, and would result in a slow rate of alkene hydrogenation. Thus, the cycloalkene is shown to be more stable due to an increase in vicinal and transannular hydrogen interations in the cycloalkene.

Inducing Room Temperature Hydrolysis of a Peptide

13a - Cis-H & Axial N-substituent	13b - Cis-H & Equatorial N-substituent	14a - Trans-H & Axial N-substituent	14b - Trans-H & Equatorial N-substituent
Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
19.7992kcal/mol	13.1633kcal/mol	12.0228kcal/mol	9.0130kcal/mol

Peptide Reaction (4 = isomer 13, 5 = isomer 14)

The energies and conformations of the above isomers were calculated using ChemBio3D and the MM2 optimisation. It was observed that the lowest energy conformations were obtained when the OH group was orientated towards the carbonyl group attached to the other ring. This is due to the possibility of Hydrogen bonding when the two groups are in close proximity. An example of this can be shown with isomer 13b, as the first conformation of this molecule was created with the OH away from the carbonyl group, giving a total energy of 17.1748kcal/mol. However, as soon as the OH was orientated towards the carbonyl group, a much lower energy of 13.1633kcal/mol was achieved.

With isomer 13, the hydrogens are cis- to each other on the ring, and the difference between 13a and 13b is the orientation of the N-substituent, either axial or equatorial in the ring. It is shown that the equatorial isomer has the lowest total energy and therefore is the most stable of the 2. This is due to the presence of 1,3-diaxial compressions in the axial isomer between the ethylamido group and the axial H on the ring.

With isomer 14, where the H are trans- in the ring, it is also the equatorial conformation which is the most energetically stable, and thus the preferred isomer, again due to 1,3-diaxial compressions with the axial conformation. This is shown by 14b having energy 9.0130kcal/mol, whilst 14a has the higher 12.0228kcal/mol. Additionally, isomer 14(both a and b) has a lower energy that isomer 13, showing the trans-H to be the more stable isomer.

Peptide Reaction (4 = isomer 13, 5 = isomer 14)

The fact that the hydrolysis of the peptide bond occurs at a much faster rate than others (which can take up to 500 years to complete) is not due to issues of strain. These isomers were in fact chosen due to the lack of strain in the amide functionality and in the steric compession between it and the hydroxyl group. This can be shown e.g. by the low stretch energies which are all approximately around 1.6kcal/mol. This faster rate is in fact due to the close proximity of the OH and the ethylamido group, which brings about favoured peptide hydrolysis. This is reinforced due to the fact that acylase enzymes are thought to bring about very rapid cleavage due to the "juxtaposition of the catylitic serine residue with the amide bond" i.e. it brings the reacting groups close together, allowing rapid cleavage of the peptide bond. Additionally, the fact that this reaction is intramolecular in contrast to other peptide cleavages which usually involve 2 molecules, means that we have a reduced rate, as the components of the reaction are all in one place. We do not have to wait for 2 molecule to come into close enough proximity.

This reaction also shows that isomer 13 carries out the hydrolysis at a much faster rate than 14. The reason for this can be seen in the diagram to the left, which shows that it is only isomer 13 which is able to undergo the intramolecular nucleophilic attack in the equatorial conformation. The lower energy conformer, and thus the major product is the isomer which undergoes the amide cleavage. In contrast, for isomer 14, the ethylamido group first has to convert to the higher energy conformer (axial position), which is the minor product, before the amide cleave can take place. This reaction with isomer 14 therefore requires energy to convert to the less energetically stable isomer before the reaction occurs, thus decreasing the rate of reaction.

Regioselective Addition of Dichlorocarbene

MM2 Optimisation Structure	Product of Hydrogenation (MM2)
Pentahelicene	Pentahelicene
Total E = 17.9004kcal/mol	Total E = 23.5844kcal/mol

The compound shown to the left (compound 12 = 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene) was first created in ChemBio3D and the molecular mechanics MM2 optimisation carried out to give the structure shown and a total energy calculated to be 17.9004kcal/mol.

Following this MM2, the HF/STO-3G self-consistent-field molecular orbital optimisation method was carried out in ChemBio3D which gave an approximation of the valence-electron molecular wavefunction. This allowed us to show the molecular orbitals on the compound, as shown in the MO table below. (HOMO-1, HOMO, LUMO, LUMO+1 & LUMO+2) A more accurate density-functional B3LYP/6-31G(d) optimisation was carried out by sending the data to scan, which also gave molecular orbitals for the compound.

The compound 12 can be hydrogenated by an electrophilic species such as dichlorocarbene or peracid. In the table to the left we can see the product of the hydrogenation in which the double C=C bond anti to the Cl (exo) has been hydrogenated, and optimised using MM2. The energy of this compound was calculated to be 23.5844kcal/mol.

Once again, the HF/STO-3G method was carried out followed by the more accurate B3LYP/6-31G(d), producing the molecular orbitals seen below:

	HF/STO-3G Optimisation of 12	B3LYP/6-31G(d)Optimisation of 12	HF/STO-3G Optimisation of product	B3LYP/6-31G(d)Optimisation of product
LUMO+2
	E = 9.736eV		12.094eV
LUMO+1
	E = 8.980eV		9.710eV
LUMO
	E = 8.572eV		8.634eV
HOMO
	E = -8.144eV		-8,398eV
HOMO-1
	E = -8.449eV		-9.387eV

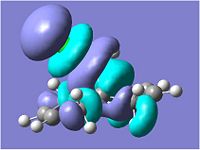
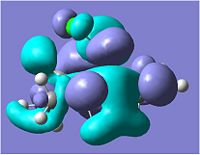
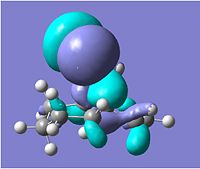
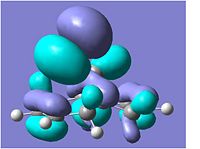
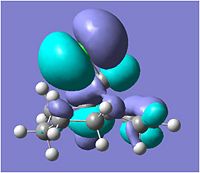
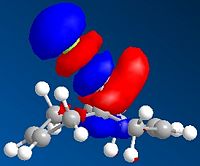
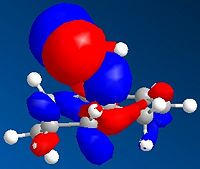
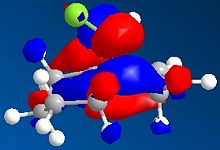
Looking at the molecular orbitals above we can see how the MOs of compound 12 affect its reactivity. Specifically, looking at the LUMO+2, HOMO and HOMO-1 molecular orbitals of compound 12, we can account for the endo regioselectivity that occurs when reacted with an electrophilic species.

This is due to the presence of stabilising anti-periplanar (app) interations between the δ^* C-Cl orbital (LUMO+2) and the C=C π bonding orbital (HOMO-1), shown on the HF/STO-3G optimisation MOs as an overlap of the red phase of the π area in HOMO-1, and the red phase of the LUMO+2 near this. Electron density can move from the bonding π C=C into the δ^* C-Cl orbital, reducing the amount of electron density in the exo C=C. Thus, this results in the exo C=C orbital HOMO-1 being stabilised in energy and being lower energy than the endo C=C MO which is the HOMO.

On hydrolysis of the exo C=C on compound 12 we can see from the orbitals that this stabilising app interaction between the δ^* C-Cl orbital (LUMO+2) and the C=C π bonding orbital (HOMO-1) is lost. There is an increase in the energy of the LUMO+2 from 9.736eV in compound 12 to 12.094eV in the hydrogenated exo C=C product.

The calculated vibrations of compound 12 and the product agree with this theory, and are shown below.

C=C vibration (exo)	C=C vibration (exo)	C=C vibration (endo)	C=C vibration (endo)	C-Cl vibration	C-Cl vibration
Freq: 1760.91cm-1	Intensity: 3.9037	Freq: 1740.76cm-1	Intensity: 4.1444	Freq: 772.634cm-1	Intensity: 25.2414

The endo C=C vibration had a frequency of 1740.76cm^-1 in contrast to the exo C=C vibration which had a frequency of 1760.91cm^-1, showing the endo C=C to be of a higher energy. This is due to the interaction of the HOMO-1 and the LUMO+2 on compound 12, which results in less vibrational energy with the exo C=C bond. With the hydrogenation product the vibrations (below)of the endo C=C stays the same on the removal of the HOMO-1 and LUMO+2 interactions. The C-Cl bond vibration also increases in energy on removal of the exo C=C bond.

C=C vibration (endo)	C=C vibration (endo)	C-Cl vibration	C-Cl vibration
Freq: 1740.58cm-1	Intensity: 3.1975	Freq: 757.729cm-1	Intensity: 27.4042

However, from looking at the B3LYP/6-31G(d) we gain an error which disagrees with the theory. Whilst the orbitals look very similar to those previously calculated, we have a problem with the fact that the MO sections of overlap of the LUMO+2 and the HOMO-1 are out of phase with each other. Thus, from looking at these orbitals we it suggests that there is no favourable overlap and thus no stabilisation. Whilst we could attribute the regioselectivity to the geometrical distorsion of the two rings, which results in overlap of the π endo C=C with the pseudo π of the cyclopropyl, the interaction is thought to be too weak to bring about the regioselective endo attack. Therefore we have to conclude that the more accurate density-functional B3LYP/6-31G(d) optimisation was not a good model for this compound, and it was in fact a more molecular mechanics model which accounted for the regioselectivity.

From observation of the journal it is suggested that there should be favourable overlap of the δ^* C-Cl bond with the π C=C of the exo double bond. (HOMO-1 with LUMO+2)This suggests that the more accurate density-functional B3LYP/6-31G(d)method's MOs are inaccurate, and it is in fact the poorer apprximation of HF/STO-3G which provided us with the more accurate representation of the orbitals. It was thought to try the PM3 method to calculate the MOs as this was carried out in the journal. The results are shown below:

no.12 HOMO-1 using PM3	no.12 LUMO+2 using PM3	Product HOMO-1 using PM3	Product LUMO+2 using PM3

Once again we can see the possibility of good overlap with the HOMO-1 and LUMO+2, along with the fact that the orbitals are in the correct phases (good overlap of the same phase - shown as red in diagrams) We can also see the loss of this overlap in the hydrogenated exo product. This allows us to conclude that a less quantum approximation is needed when calculating and oserving MOs for particular molecules, and the less accurate HF/STO-3G and PM3 methods showed the MOs in the expected phases, whilst the most accurate B3LYP/6-31G(d) gave us the orbital overlap with the wrong phases.

Structure based Mini project using DFT-based Molecular orbital methods

Assigning regioisomers in "Click Chemistry"

Reaction	General Mechanism

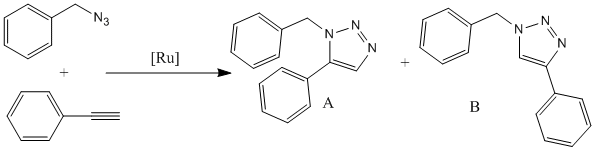
The reaction shown to the right is a Ru-catalyzed cycloaddition of benzyl azide with phenylacetylene.

There are two possible regioisomeric products of this reaction, with the major product dependent on the type of catalyst used for the cycloaddition. For example, A is the major product (100%) with the catalyst Cp^*RuCl(PPh₃)₂, whilst B is the major with catalyst Ru(OAc)₂(PPh₃)₂, and is also known to be the major product with the use of Cu catalysists, such as Cu/AlO(OH) which gave product B as the major with 94% yield.

The general mechanism can also be seen, which shows the catalyst, in this case Ru, co-ordinating to the N of the N₃ group and the alkyne carbon-carbon triple bond. This bond undergoes hydrolysis followed by the addition of the third N onto the carbon-carbon double bond. The two groups then detach from the catalyst to form the ring. The orientation of the double bond when co-ordinating to the catalyst will determine the position of the R group, in this case the phenyl group, as the N can attach to the carbon with or without the R group attached. This therefore gives the observed 2 possible products.

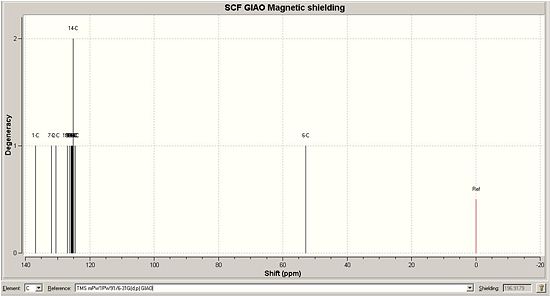
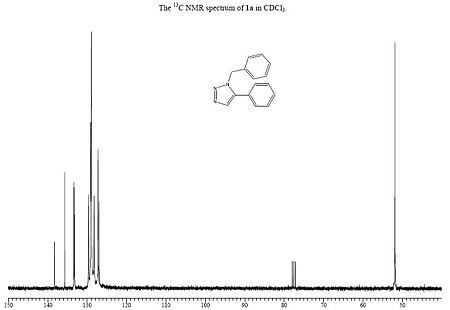
Below are the calculated ¹³C NMR for the two products A and B, along with the images of the real ¹³C NMR spectra:

Calculated 13C NMR for A DOI:10042/to-1165	Real 13C NMR spectra for A
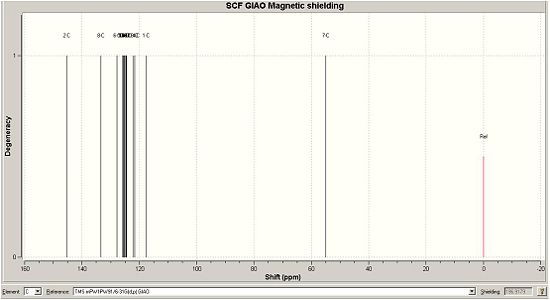
Calculated 13C NMR for B DOI:10042/to-1169	Real 13C NMR spectra for B

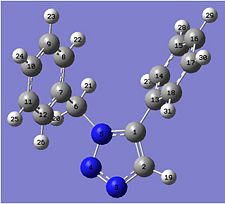
Below is a representation of both A and B, with the atoms numbered, corresponding to the labels of the calculated NMRs:

A	B

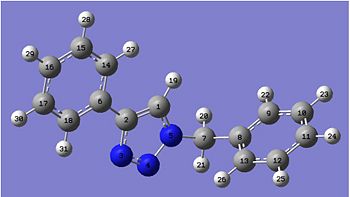
When looking at the NMR values for both calculated A and B, we can see some significant differences between the two spectra. The first of these is the C of the methylene group, which is shown as C6 for compound A and C7 for compound B. This peak has a relatively low ppm, 52.77ppm for A and 54.96ppm for B, showing A to best match the peak on the given NMR in the journal provided. Another difference between the two can be seen by the range of many peaks being slighty different. For A, there are 11 peaks very close to each other in the range of 124ppm - 130ppm, whilst B has 10 peaks in a smaller range of 121ppm - 127ppm. These peaks correspond to the aromatic carbon atoms, and also shows that B has a general lower ppm than A for these values. An NMR for compound B was found in the Cu catalysed journal and this is shown below. It can be seen that this is a better match to compound B than the previous NMR values, expecially due to the presence of the shift around 145-148ppm, which is a smaller value around 135ppm for the given and calculated NMR for A. There is inaccuracies in both of the calculated values, as most are wrong by about a factor of 1-3ppm.

A greater number of shifts were calculated in comparison to the real NMR, but this is due to the fact that the calculation doesnt take into account the resolution of the NMR and so on the real one, the fewer peaks is due to peaks merging. Also, the calculation does not take into account coupling, so this is not observed on the spectra. However, this method of calculating ¹³C NMR shifts is sufficient to determine the isomer obtained, as there are suffienient differences in the position of the peaks on the two NMRs to make a clear distinction between them.

Literature 13C NMR shift for A (ppm)	Calculated 13C NMR shift for A (ppm)		Literature 13C NMR shift for B (ppm)	Calculated 13C NMR shift for B (ppm)
51.85	52.770		54.681	54.9622
126.93; 127.22; 128.22; 128.92; 129.08; 129.64; 133.26; 133.34	124.445; 124.816; 125.1430; 125.171; 125.415; 125.544; 125.646; 125.808; 126.283; 126.977; 130.527		120.93	117.683
135.66	131.953		126.223; 128.562; 128.688; 129.269; 129.351; 129.658; 131.112	121.650; 122.210; 124.710; 124.813; 125.188; 125.257; 125.381; 125.585; 125.893; 127.771
138.26	136.867		135.291	133.401
			148.689	145.340

References

NMRs are present in supplementary information of references 6 and 7.