Rep:Mod:mwc14 y3c LS

General Comments: This is really good and written to a high standard. Although, you didn't quite conclude/use the right timestep you had the right idea throughout. Mark 78/100 Liquid Simulations

Submitted by Michael W. H. Cheung (mwc14)

Theory

Numerical Integration

TASK: Open the file HO.xls. In it, the velocity-Verlet algorithm is used to model the behaviour of a classical harmonic oscillator. Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY": "ANALYTICAL" should contain the value of the classical solution for the position at time $t$, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution (i.e. ERROR should always be positive -- make sure you leave the half step rows blank!), and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$ (the values of $A$, $\omega$, and $\varphi$ are worked out for you in the sheet).

Ans: The data generated for "ANALYTICAL", "ERROR", and "ENERGY" can be found here.

Position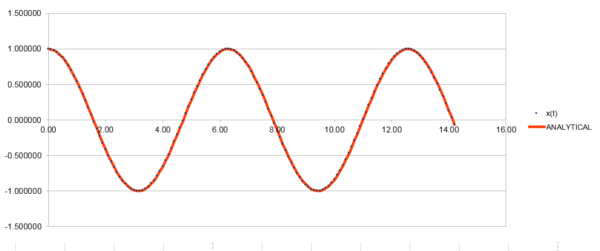
Error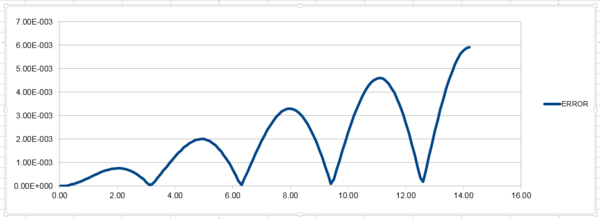
Energy

TASK: For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

Ans: The following graph shows the local maxima of the error versus time, and the trend line plotted.

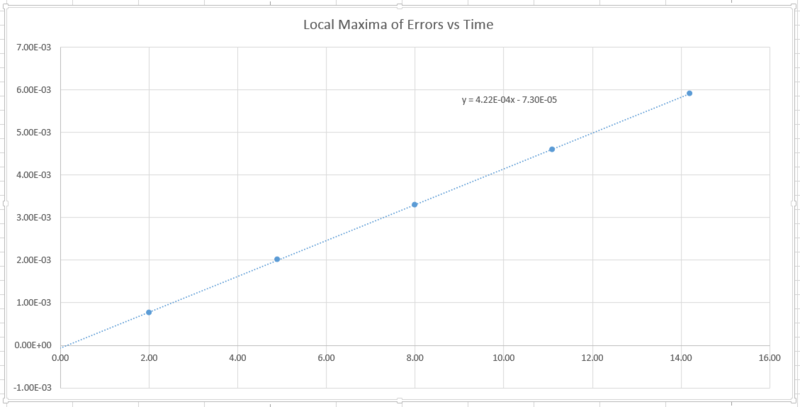
TASK: Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?

Ans: An decrease in timestep reduces the variation of the total energy, while an increase in timestep increases the variation. When the timestep is larger than 0.2, the total energy varies more than 1%; therefore, the timestep should be $\le 0.2$. Tick

It is important to monitor the total energy, because according to the first law of thermodynamics, energy is conserved in a isolated system. Therefore, the total energy in a physical system should be constant. When modelling its behaviour, it is thus essential to ensure that the total energy is constant.

Atomic Forces

TASK: For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$.

Ans: The separation, $r_0$, at which the potential energy is zero, is equal to $\sigma$.Tick
Using the equation, $F=-\frac{dU}{dr}=-\frac{d}{dr}\varphi (r)$,

$F=-\frac{d}{dr}4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})=-4ϵ(-12\frac{{\sigma }^{12}}{r^{13}}+6\frac{{\sigma }^6}{r^7})=4ϵ(12\frac{{\sigma }^{12}}{r^{13}}-6\frac{{\sigma }^6}{r^7})$

When $r=\sigma$,

$F=4ϵ(12\frac{{\sigma }^{12}}{{\sigma }^{13}}-6\frac{{\sigma }^6}{{\sigma }^7})=4ϵ(\frac{12}{\sigma }-\frac{6}{\sigma })=4ϵ\left(\frac{6}{\sigma }\right)=\frac{24ϵ}{\sigma }$

Tick

Therefore, the force at this separation is $\frac{24ϵ}{\sigma }$.
The equilibrium separation, $r_{eq}$, is calculated at which $\frac{d}{dr}\varphi (r)=0$. Using the equation above, $\frac{d}{dr}\varphi (r)=4ϵ(-12\frac{{\sigma }^{12}}{r^{13}}+6\frac{{\sigma }^6}{r^7})$,

$4ϵ(-12\frac{{\sigma }^{12}}{{r_{eq}}^{13}}+6\frac{{\sigma }^6}{{r_{eq}}^7})=0$

$-12\frac{{\sigma }^{12}}{{r_{eq}}^{13}}+6\frac{{\sigma }^6}{{r_{eq}}^7}=0$

$\frac{-2{\sigma }^{12}}{{r_{eq}}^{13}}+\frac{{\sigma }^6}{{r_{eq}}^7}=0$

$\frac{-2{\sigma }^{12}+{\sigma }^6{r_{eq}}^6}{{r_{eq}}^{13}}=0$

Since $$\begin{gathered} r_{eq}\ne 0, \\ -2{\sigma }^{12}+{\sigma }^6{r_{eq}}^6=0 \end{gathered}$$

Dividing by${\sigma }^6,{r_{eq}}^6-2{\sigma }^6=0$

${r_{eq}}^6=2{\sigma }^6$

$r_{eq}=\sqrt[6]{2}\sigma$

Tick

Therefore, $\varphi \left(r_{eq}\right)=4ϵ(\frac{{\sigma }^{12}}{{r_{eq}}^{12}}-\frac{{\sigma }^6}{{r_{eq}}^6})=4ϵ(\frac{{\sigma }^{12}}{{\left(\sqrt[6]{2}\sigma \right)}^{12}}-\frac{{\sigma }^6}{{\left(\sqrt[6]{2}\sigma \right)}^6})=4ϵ(\frac{{\sigma }^{12}}{4{\sigma }^{12}}-\frac{{\sigma }^6}{2{\sigma }^6})$

$=4ϵ(\frac{1}{4}-\frac{1}{2})=4ϵ(-\frac{1}{4})=-ϵ$

Tick

Thus, $\varphi (r_{eq})=-ϵ$.

Evaluating the integrals, $\underset{a}{\overset{b}{\int }}\varphi \left(r\right)\mathrm{d}r$, where $\sigma =ϵ=1.0,$

$\underset{a}{\overset{b}{\int }}\varphi (r)dr=\underset{a}{\overset{b}{\int }}4(\frac{1}{r^{12}}-\frac{1}{r^6})dr={\left[4(-\frac{1}{11r^{11}}+\frac{1}{5r^5})\right]}_a^b$

When $a=2,b=\mathrm{\infty },\underset{2}{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr={\left[4(-\frac{1}{11r^{11}}+\frac{1}{5r^5})\right]}_2^{\mathrm{\infty }}=0-(-\frac{4}{11\times 2^{11}}+\frac{4}{5\times 5^{11}})=-0.0248$Tick

When $a=2.5,b=\mathrm{\infty },\underset{2.5}{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr={\left[4(-\frac{1}{11r^{11}}+\frac{1}{5r^5})\right]}_{2.5}^{\mathrm{\infty }}=0-(-\frac{4}{11\times {2.5}^{11}}+\frac{4}{5\times {2.5}^{11}})=-0.0082$Tick

When $a=3,b=\mathrm{\infty },\underset{3}{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr={\left[4(-\frac{1}{11r^{11}}+\frac{1}{5r^5})\right]}_3^{\mathrm{\infty }}=0-(-\frac{4}{11\times 3^{11}}+\frac{4}{5\times 3^{11}})=-0.0033$Tick

Periodic Boundary Conditions

TASK: Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of $10000$ water molecules under standard conditions.

Ans: The density of water is 1 g cm^-3, so 1 mL of water contains 1 g of water molecules. The molar mass of water is 18.01528 g mol^-1, so 1 g of water is equal to 0.0555 mol of water, that is $3.34\times 10^{22}$ water molecules. Tick

10000 water molecules equal to $1.66\times 10^{-22}$ mol of water, which is $2.99\times 10^{-19}$g. Since the density of water is 1 g cm^-3, the volume of 10000 water molecules is $2.99\times 10^{-19}$ cm ^-3. Tick

TASK: Consider an atom at position $(0.5,0.5,0.5)$ in a cubic simulation box which runs from $(0,0,0)$ to $(1,1,1)$. In a single timestep, it moves along the vector $(0.7,0.6,0.2)$. At what point does it end up, after the periodic boundary conditions have been applied?.

Ans: The atom ends up at position $(0.2,0.1,0.7)$.Tick

Reduced Units

TASK: The Lennard-Jones parameters for argon are $$\begin{gathered} \sigma =0.34\mathrm{n}\mathrm{m},ϵ \\ / \\ {k}_B=120\mathrm{K} \end{gathered}$$. If the LJ cutoff is $r^{*}=3.2$, what is it in real units? What is the well depth in $$\begin{gathered} {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$? What is the reduced temperature $T^{*}=1.5$ in real units?

Ans: Rearranging the formula $r^{*}=\frac{r}{\sigma }$, $r=\sigma r^{*}=3.2\times 0.34\times {10}^{-9}=1.088\times {10}^{-9}m$. Tick

The well depth is $$\begin{gathered} ϵ=120\mathrm{K}\times k_B=0.996 \\ {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$. Tick

Rearranging the formula $T^{*}=\frac{k_{B}T}{ϵ}$, $T=T^{*}\frac{ϵ}{k_B}=1.5\times 120=180\mathrm{K}$.Tick

Equilibration

Creating the simulation box

TASK: Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

Ans: If atoms are given random starting coordinates, such that in case two atoms are generated too close together, they might overlap and cause interatomic energies and large values of forces. This is unrealistic and will cause the simulation to be inaccurate. Tick and we would need to use an excessively small timestep

TASK: Satisfy yourself that this lattice spacing corresponds to a number density of lattice points of $0.8$. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?

Ans: The volume of the cell is $$\begin{gathered} \frac{number \\ of \\ atoms}{lattice \\ point \\ density} \end{gathered}$$. As it is a cubic cell, the side length of the unit cell is the cube root of the volume. For the 0.8 case, since there is 1 atom, and the side length is 1.07722, the density is thus $\frac{1}{{1.07722}^3}=\frac{1}{1.25}=0.8$ For a cubic cell with a lattice point number density of 1.2, the side length is $\sqrt[3]{\frac{4}{1.2}}=1.4938$.Tick

TASK: Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?

Ans: For a simple cubic lattice, 1000 atoms were created, because a box of $10\times 10\times 10$ was defined. A simple cubic lattice has 1 atom per cell, therefore 1000 atoms were created. A face-centered cubic lattice has 4 atoms per cell, so if that lattice was defined, 4000 atoms would be created. Tick

Setting the properties of the atoms

TASK: Using the LAMMPS manual, find the purpose of the following commands in the input script:

mass 1 1.0
pair_style lj/cut 3.0
pair_coeff * * 1.0 1.0

Ans: mass 1 1.0 defines the mass of the atoms, such that the first number 1 defines which type of atoms to define, and the second 1.0 defines the mass of those types of atoms.

The command pair_style tells LAMMPS to calculate pairwise interactions using which formulae. In this case, pair_style lj/cut 3.0, it tells LAMMPS to calculate the Lennard-Jones potential, $E=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, where 3.0 is the cutoff value. pair_coeff defines the coefficients $ϵ,\sigma$ cutoff value 1 and cutoff value 2 respectively.Tick

TASK: Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?

Ans: The velocity-Verlet algorithm will be used. Tick

Running the simulation

TASK: Look at the lines below.

### SPECIFY TIMESTEP ###
variable timestep equal 0.001
variable n_steps equal floor(100/${timestep})
variable n_steps equal floor(100/0.001)
timestep ${timestep}
timestep 0.001

### RUN SIMULATION ###
run ${n_steps}
run 100000

The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write:

timestep 0.001
run 100000

Ask the demonstrator if you need help.

Ans: By writing the SPECIFY TIMESTEP lines, the amount of time each simulation runs is constant, i.e. 100, even under variable timesteps. This is achieved by telling the computer Not the most scientific of language! to compute how many runs are necessary for the specific simulation, instead of computing the number of runs manually when the timestep is changed. This makes the simulations with different timesteps easily comparable. Tick, general principles of variable definition

Checking equilibration

TASK: make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

Ans: Below shows the graphs plotted from the data of the 0.001 timestep.

The simulation reaches equilibrium at about time 0.5.

The table below shows the plots of energy versus time of different timesteps.

Timestep	Plot
0.001
0.0025
0.0075
0.01
0.015

As is shown, the energy for all simulations except for timestep 0.015 reaches an equilibrium. Therefore, timestep 0.001 is the largest to give acceptable results, and timestep 0.015 is a particularly bad choice, because the system simulated does not have energy conservation, which is unrealistic.Not quite right. 0.0025 is the largest timestep to provide a converged total energy... You would be able to see this if you plotted all the total energies for different timesteps on the same plot

Running simulations under specific conditions

Thermostats and Barostats

TASK: We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations:

$\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$

$\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2=\frac{3}{2}N{k}_B\mathfrak{𝔗}$

Solve these to determine $\gamma$.

Ans: Dividing equation 2 by equation 1,

$\frac{\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2}{\frac{1}{2}\sum _i{m}_i{v}_i^2}=\frac{\frac{3}{2}N{k}_B\mathfrak{𝔗}}{\frac{3}{2}N{k}_{B}T}$

${\gamma }^2=\frac{\mathfrak{𝔗}}{T}$

$\gamma =\pm \sqrt{\frac{\mathfrak{𝔗}}{T}}$

Tick

Examining the Input Script

TASK: Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate?

Ans: When 100 1000 100000 is input in the script, the values of temperature, etc., will be averaged every 100000 timesteps. The average is computed by averaging 1000 previous measurements, with a step of 100 timesteps. If timestep 0.001 was chosen, the values of timestep 0, 100, 200, 300, ... , 99700, 99800, 99900 and 100000 is averaged to give the average on timestep 100000. 1000 measurements contribute to the average. The simulation will be run for 100000 timesteps, in this case, $100000\times 0.01=100$. For your computationally expensive timestep, this is true..

Plotting the Equations of State

TASK: When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

Ans: Below shows the plots of density versus temperature at different pressures.

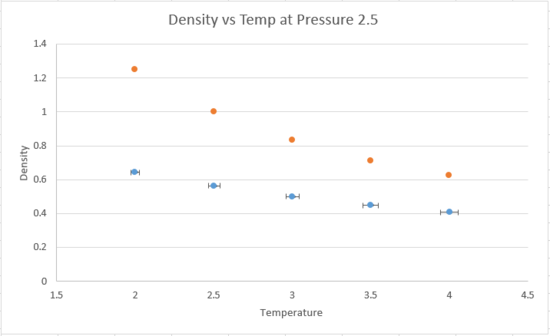
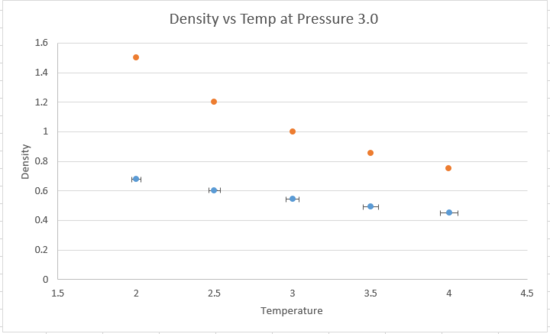
The blue points are the simulated density values, while the orange points are the density values predicted by the ideal gas law. The simulated density is lower than the predicted ones, because the ideal gas law makes many assumptions, for example in an ideal gas, atoms next to each other do not interact, thus ignoring repulsion between atoms, thereby generating a higher density value than the simulated ones. The simulated density values were computed using Lennard-Jones potential, which gives rise to interacting energy between atoms. The discrepancy increases with increasing pressure, shown below. Tick

	Difference between simulated density and predicted density
Temperature	At pressure 2.5	At pressure 3.0
2.0	0.605880726	0.821275217
2.5	0.435715223	0.595782337
3.0	0.332991083	0.457166088
3.5	0.265663811	0.365007887
4.0	0.218209322	0.300144938

Calculating heat capacities using statistical physics

TASK: As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at $0.2$ and $0.8$, and the temperature range is $2.0,2.2,2.4,2.6,2.8$. Plot $C_V/V$ as a function of temperature, where $V$ is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.

Ans: Below is the graph.

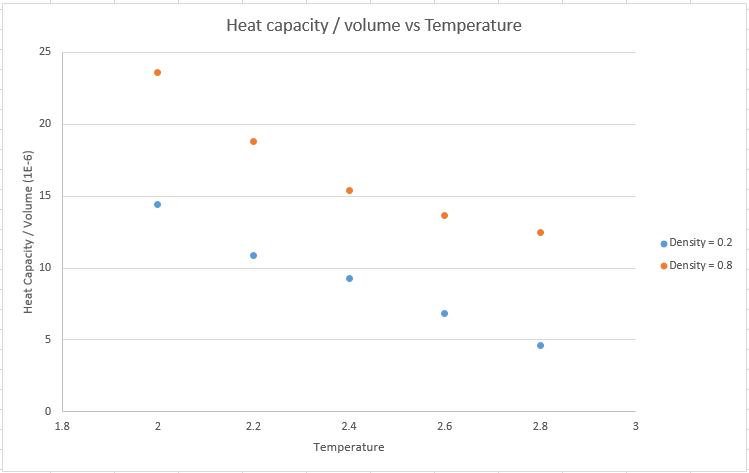
From the graph, there is an negative trend between heat capacity and temperature, with a higher heat capacity with higher density. Since heat capacity is the ability of a material to excite electrons into higher energy levels. With increased temperature, more energy levels become populated, thus reducing the ability of other electrons exciting to higher energy levels, thus a lower heat capacity at increased temperature. The total energy of the solid also increases with increasing temperature, which indicates that higher energy levels are occupied, providing evidence to the argument. Hmm in terms of internal energy, how would this manifest?

The heat capacity for density 0.8 is higher than that for density 0.2. Since the NVT ensemble is simulated, the volume is kept constant. Therefore, an increase in density means an increase in mass. Because of the increased mass, there are more accessible energy levels, which allows more electrons to be excited to a higher energy level at the same temperature, thus the increased values for heat capacity.

One of the input script of the simulation is attached below. This is the input script for density 0.8, temperature 2.0.

### DEFINE SIMULATION BOX GEOMETRY ###
lattice sc 0.8
region box block 0 15 0 15 0 15
create_box 1 box
create_atoms 1 box

### DEFINE PHYSICAL PROPERTIES OF ATOMS ###
mass 1 1.0
pair_style lj/cut/opt 3.0
pair_coeff 1 1 1.0 1.0
neighbor 2.0 bin

### SPECIFY THE REQUIRED THERMODYNAMIC STATE ###
variable T equal 2.0
variable timestep equal 0.001

### ASSIGN ATOMIC VELOCITIES ###
velocity all create ${T} 12345 dist gaussian rot yes mom yes

### SPECIFY ENSEMBLE ###
timestep ${timestep}
fix nve all nve

### THERMODYNAMIC OUTPUT CONTROL ###
thermo_style custom time etotal temp press
thermo 10

### RECORD TRAJECTORY ###
dump traj all custom 1000 output-1 id x y z

### SPECIFY TIMESTEP ###

### RUN SIMULATION TO MELT CRYSTAL ###
run 10000
unfix nve
reset_timestep 0

### BRING SYSTEM TO REQUIRED STATE ###
variable tdamp equal ${timestep}*100
fix nvt all nvt temp ${T} ${T} ${tdamp}
run 10000
reset_timestep 0
unfix nvt
fix nve all nve 

### MEASURE SYSTEM STATE ###
thermo_style custom step etotal temp press density atoms
variable dens equal density
variable dens2 equal density*density
variable temp equal temp
variable temp2 equal temp*temp
variable press equal press
variable press2 equal press*press
variable etotal equal etotal
variable etotal2 equal etotal*etotal
variable atoms equal atoms
fix aves all ave/time 100 1000 100000 v_dens v_temp v_press v_dens2 v_temp2 v_press2 v_etotal v_etotal2
run 100000

variable avedens equal f_aves[1]
variable avetemp equal f_aves[2]
variable ave_t2 equal ${avetemp}*${avetemp}
variable avepress equal f_aves[3]
variable ave_esq equal f_aves[7]*f_aves[7]
variable ave_e2 equal f_aves[8]
variable errdens equal sqrt(f_aves[4]-f_aves[1]*f_aves[1])
variable errtemp equal sqrt(f_aves[5]-f_aves[2]*f_aves[2])
variable errpress equal sqrt(f_aves[6]-f_aves[3]*f_aves[3])

variable hcap equal ${atoms}*${atoms}*(${ave_e2}-${ave_esq})/${ave_t2}

print "Averages"
print "--------"
print "Density: ${avedens}"
print "Stderr: ${errdens}"
print "Temperature: ${avetemp}"
print "Stderr: ${errtemp}"
print "Pressure: ${avepress}"
print "Stderr: ${errpress}"
print "Heat Cap: ${hcap}"

Structural properties and the radial distribution function

TASK: Perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate $g(r)$ and $\int g(r)\mathrm{d}r$. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

Ans: Below shows the graphs $g(r)$ and $\int g(r)$ versus r.

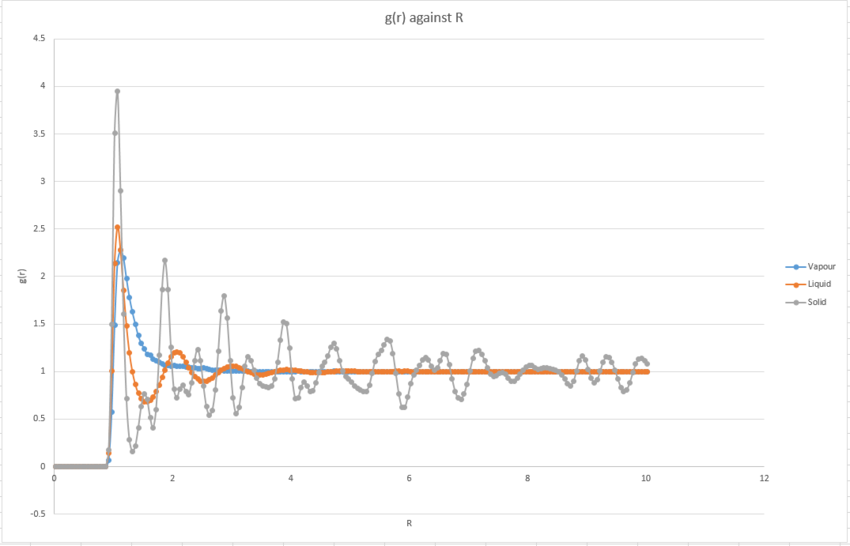
The radial distribution function (RDF) is a measure of how probable it is to find the next atom at a given radius from the measured atom. In the vapour phase, the curve converges to 1 shortly after reaching a peak at about R=1. This is evidence that the fluid in the vapour phase is very disordered, especially after 1 radius length. In the liquid phase, there exist a few peaks, before again converging to 1. This shows that in the liquid phase the fluid has more order than the vapour phase, but lacks long-ranged order ultimately. In the solid phase, there are evident peaks on the plot, which still exist even after R=10. This shows that the solid phase is very ordered and the position of these peaks tells the position of the next atom. However, compared to the vapour and liquid plots, the solid phase plot shows many fluctuations. This could be explained by the constrained nature of the atoms in the solid phase, where atoms are more rigid than in the liquid and vapour phase, thus creating such a rough plot. Tick

The first three peaks, (1.075, 3.951), (1.525, 0.767) and (1.875, 2.166) correspond to atoms 1, 2 and 3 respectively, with the red atom as the reference atom. The lattice spacing corresponds to the distance between the red atom and atom 2, which is 1.525. The coordination number for these peaks are 12, 6 and 24.Tick

Dynamical properties and the diffusion coefficient

Simulations in this Section

TASK: In the D subfolder, there is a file liq.in that will run a simulation at specified density and temperature to calculate the mean squared displacement and velocity autocorrelation function of your system. Run one of these simulations for a vapour, liquid, and solid. You have also been given some simulated data from much larger systems (approximately one million atoms). You will need these files later.

Mean Squared Displacement

TASK: make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate $D$ in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

Ans: The following table shows the plots of MSD in different phases and different number of atoms.

MSD for	Solid	Liquid	Vapour
8000 atoms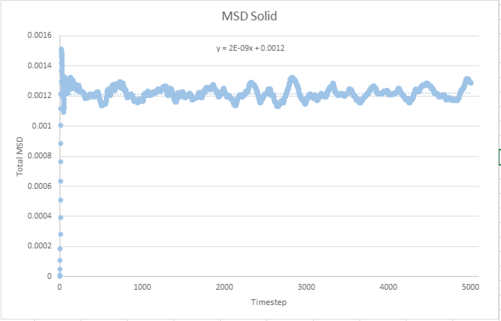
1 million atoms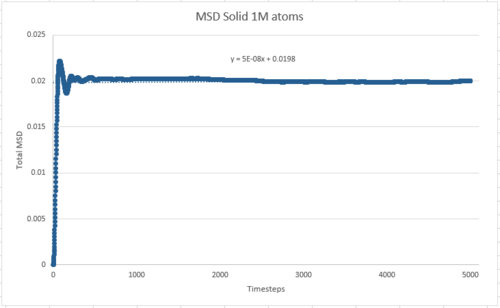

Using the formula, $D=\frac{1}{6}\frac{\partial ⟨r^2\left(t\right)⟩}{\partial t}$, where the gradient gives $r^2(t)and<math>\partial t$ being 0.002, the timestep used in these simulations, the diffusion coefficients are calculated as follows.

Diffusion coefficient using MSD
Atoms	Solid	Liquid	Vapour
8000	1.67×10-7	0.0833	2.53
1 million	4.17×10-6	0.0833	2.54

From the table, the diffusion coefficient increases as the phase changes from solid to liquid to vapour. It is the expected trend, since the atoms in solid phase are constrained and cannot move around easily, which indicates a low diffusion rate and therefore a low diffusion coefficient. In the liquid phase, the atoms are able to move around more freely than in the solid phase, but not as freely as in the vapour phase. In the vapour phase, atoms are completely disordered; therefore, the atoms are free to diffuse anywhere, and thus explains the highest diffusion coefficient among three phases.Tick

From the values of diffusion coefficient, the simulations with either 8000 atoms or 1 million atoms do not differ greatly. Even if the solid phase diffusion coefficients differ by 1 magnitude, it is efficiently small enough to provide evidence such that the diffusion for a solid is significantly lower than that in a liquid or a vapour. Moreover, the shapes of the plots are similar between simulations, with the 8000-atom solid-phase simulation fluctuating in latter timesteps. This could be explained by the averaging technique of the simulation, where the averaging is less accurate in 8000 atoms than in 1 million atoms.Tick

Velocity Autocorrelation Function

TASK: In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!):

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

Ans: From the theoretical section, $x\left(t\right)=A\cos (\omega t+\varphi )$ and $v(t)=\frac{dx(t)}{dt}$.

Therefore,

$v(t)=-\omega A\sin (\omega t+\varphi )$

Substituting this into the equation, $C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$,

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

$=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(-\omega A\sin (\omega t+\varphi ))(-\omega A\sin (\omega (t+\tau )+\varphi ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(-\omega A\sin (\omega t+\varphi ){)}^2\mathrm{d}t}$

$=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\omega A\sin (\omega t+\varphi ))(\omega A\sin (\omega t+\varphi +\omega \tau ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\omega }^2{A}^2{\sin }^2(\omega t+\varphi ))\mathrm{d}t}$

$=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\omega A\sin (\omega t+\varphi ))(\omega A\sin (\omega t+\varphi )\cos (\omega \tau )+\cos (\omega t+\varphi )\sin (\omega \tau ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\omega }^2{A}^2{\sin }^2(\omega t+\varphi ))\mathrm{d}t}$

$=\frac{{\omega }^2{A}^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\sin (\omega t+\varphi ))(\sin (\omega t+\varphi )\cos (\omega \tau )+\cos (\omega t+\varphi )\sin (\omega \tau ))\mathrm{d}t}{{\omega }^2{A}^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\sin }^2(\omega t+\varphi ))\mathrm{d}t}$

$=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\sin }^2(\omega t+\varphi )\cos (\omega \tau )+\sin (\omega t+\varphi )\cos (\omega t+\varphi )\sin (\omega \tau ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\sin }^2(\omega t+\varphi ))\mathrm{d}t}$

$=\cos (\omega \tau )+\frac{\sin (\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\sin (\omega t+\varphi )\cos (\omega t+\varphi ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}({\sin }^2(\omega t+\varphi ))\mathrm{d}t}$

$=\cos (\omega \tau )$

Tick

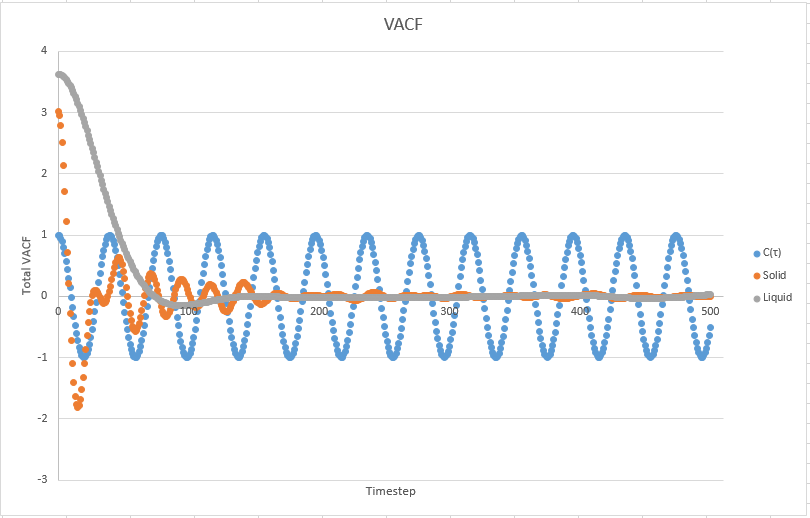
Below is a plot of the VACF of $C(\tau )$, solid and liquid against time.

The VACF graph shows the change of velocity at a specific timestep, such that if the atoms in the system do not have any interactions, the plot will be completely horizontal. However, this is not the case in all of three plots. In the solid system, the plot oscillates even when it reaches time 500. In the liquid system, the plot reaches a minima near time 80 and then remains horizontal. These minima represent the atoms' movement to find an energentically stable state, where the direction and the magnitude of the movement are represented in the VACF values. Tick

In the solid system, the interatomic forces are large, and the atoms are not able to diffuse easily. Therefore, the solid system oscillates for a large amount of time to find the most energetically stable state, and thus the occurence of so many minima in the solid system. In the liquid system, the atoms are no longer fixed at regular positions, therefore, it only reaches one minima, and continues to be horizontal as it finds its equilibrium at VACF = 0. This symbolizes that atoms no longer attain velocity at those times. To an extent, yes! Think about the time at which all the particles have first collided

The harmonic oscillator VACF is significantly different, because it does not hold account to the attractive and repulsive forces among atoms, which is taken account in a Lennard-Jones simulation. As such, the atoms in such a system oscillates indefinitely, because of the lack of force simulation.Tick

Integral of VACF

TASK: Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate $D$ in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

Ans: Below are the plots of the integral of VACF against timestep.

Integral of VACF for	Solid	Liquid	Vapour
8000 atoms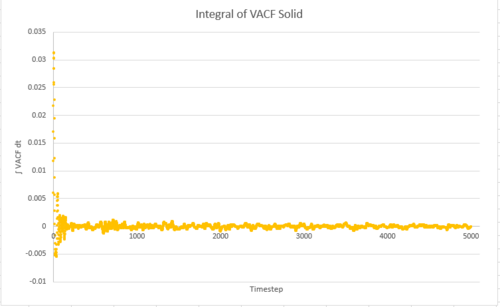
1 million atoms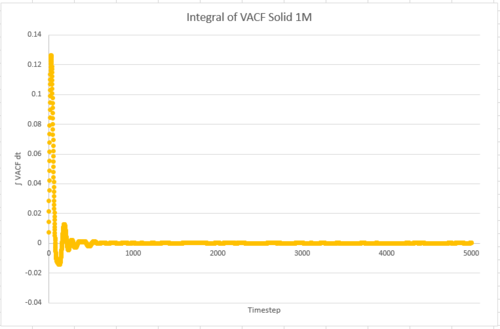

Using the formula, $D=\frac{1}{3}\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}\tau ⟨\mathbf{v}\left(0\right)\cdot \mathbf{v}\left(\tau \right)⟩$, the diffusion coefficients are calculated.

Diffusion coefficient using VACF
Atoms	Solid	Liquid	Gas
8000	4.73×10-5	0.0978	3.29
1 million	4.55×10-5	0.0901	3.27

Comparing the values of D calculated by VACF to that calculated by MSD, all values calculated by VACF are slightly higher than the values calculated by MSD. The increasing D from solid to gas is expected, as outlined previously in the MSD section. There is also only a slight difference between the simulation of 8000 atoms and 1 million atoms, which is less than the difference calculated using MSD. Thus, using MSD and VACF, two distinct methods, the diffusion coefficient in different systems can be calculated, yielding satisfying and similar results in both cases. Tick

The largest source of error occurs in the method of calculation in computing the integral of VACF. Here, the trapezium rule is used, which regards curves as straight segments and estimates the area under the curve. In the case of a large curvature, the trapezium rule will likely give erroneous results, because it approximates a curve into a line. As the running integral is a sum of the previous integrals, the error carries forward into the final result. This means that a small error in each of the trapezium would turn into a huge error at the end. To solve this problem, longer timesteps can be used to split the curve into finer pieces, which then the error will possibly be minimized, with the cost of running the simulation in a longer period of time. Moreover, the simulation itself contributes to error, with the inclusion of averaging within the system, and random error arising from the atoms in the simulation.Tick, good