Rep:Mod:mw1409module1

Modelling using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Caption

When cyclopentadiene dimerises there are two possible outcomes, the exo product 1 and the endo product 2. The endo dimer is the major product. When this is hydrogenated two possible dihydro products can form, dihydro derivatives 3 and 4.

ChemBio 3D was used to define the dimers 1 and 2 and their geometries were optimised using the MM2 force field. The results (see table below) show that overall the endo dimer 2 is the highest in energy of the two with a total energy of 142.25kJmol^-1 compared with 133.37kJmol^-1 for the exo dimer 1. This means that the endo dimer is thermodynamically less stable than the exo dimer and would be less favoured if the reaction was thermodynamically controlled. The reaction is in fact selective for the endo dimer. This shows that the reaction occurs under kinetic control. The transition state for the formation of the endo product is more stabilised that that for the exo product so the endo route is mechanistically preferred. Comparing the relative energies of the dihydro derivatives 3 and 4 it can be seen that 4 is lower in energy. This shows that it is the most stable isomer and therefore would be expected to be the major product if the reaction proceeds under thermodynamic control. The relative contributions of the different energy terms can be compared to analyse the cause of this reduction in total energy. The most significant term observed is that for the bending energy contribution. For molecules 1, 2, and 3 the contributions are 86.10kJmol^-1, 87.23kJmol^-1 and 83.13kJmol^-1 respectively. These are all fairly similar with a slight drop in energy for the dihydro derivative 3 due to the release of angle strain allowed by the opening of the C=C bond. For the dihydro derivative 4 however there is a drop of over 20kJmol^-1 in the energy of the bending energy contribution to just 60.77kJmol^-1. This can be rationalised by comparing the structures of 3 and 4. In the dihydro derivative 3 the unsaturated bond that is hydrogenated is the one located in the cyclopentene ring whereas in derivative 4 the unsaturated bond is located in the 6-membered cyclohexene ring. A cyclohexane ring is a lower energy conformation than a cyclopentane ring as the bond angles are not as restricted. The energy reduction on going from a cyclopentene to a cyclopentane is therefore smaller than that achieved in going from a cyclohexene to a cyclohexane.

Energy Contributions / kJ mol-1	Exo Dimer 1	Endo Dimer 2	Dihydro Derivative 3	Dihydro Derivative 4
Stretch	5.38	5.23	5.35	4.59
Bend	86.10	87.23	83.13	60.77
Stretch-Bend	-3.51	-3.50	-3.49	-2.30
Torsion	32.04	39.79	45.20	52.29
Non-1,4 VDW	-5.93	-6.46	-5.13	-4.48
1,4 VDW	17.71	18.07	23.57	18.88
Dipole/Dipole	1.58	1.87	0.68	0.59
Total Energy	133.37	142.25	149.31	130.34

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Caption

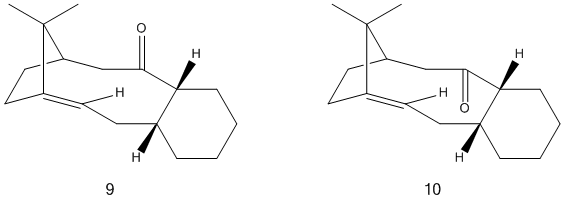
The oxy-Cope rearrangement is a valuable tool in organic synthesis. Used as a key step in the synthesis of Taxol it can result in the formation of two atropisomers, intermediates 9 and 10, that differ in the orientation of the carbonyl group on the ring. In inetrmediate 9, the carbonyl group points up and in intermediate 10 the carbonyl group point down. A molecular mechanics MM2 force field was used to minimise the energies of both conformations. From this the total energy of intermediate 9 was determined to be 200.2kJmol^-1 and that for intermediate 10 was determined to be 178.6kJmol^-1. Following this initial minimisation, attempts were made to manipulate the structures of both conformations and further minimise the total energy. However both structures have the cyclohexane ring in a chair conformation which is the lowest energy for that part of the molecule and further changes to other parts did not result in a lowering of the overall energy. The minimised structures of 9 and 10 are shown below, with an image intermediate 10 shown with the chair conformation of the cyclohexane ring clearly highlighted.

Intermediate 9	Intermediate 10	Intermediate 10 with chair conformation of cyclohexane ring highlighted

Since intermediate 10 was determined to be the lowest energy conformation, it can be concluded that upon standing the mixture of products slowly isomerises to give a pure sample of 10. This means that 10 is the most stable isomer and hence the thermodynamic product. The functionalisation of the C=C bond in 10 is a slower reaction than would be expected for a bridgehead olefin.Generally C=C bonds tend to avoid ring junctions as there is more limited conformational flexibility and the bond as a result tends to be more strained. However in some cases a bridgehead olefin can be less strained than the corresponding cycloalkane and are therefore very stable. These are unreactive as the double bond confers greater stability than they would have if the bond was to be opened. This is the case for ring systems with a trans double bond. When the MMFF94 force field is used to minimise the energy, the vastly different values of 295.1kJmol^-1 and 253.3kJmol^-1 are obtained for 9 and 10 respectively. These values differ as the force fields are designed for different applications. however they both agree that the intermediate 10 is the thermodynamically most stable.

Modelling Using Semi-Empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Caption

Computational methods can be used to predict the outcome of reactions under orbital control as the orbital energy can be calculated and the form of the molecular orbitals displayed. Compound 12 is a diene that can undergo reactions with electrophilic reagents. Looking at the molecular orbitals of the compound can give an idea of the reactivity by showing the most nucleophilic C=C. Initially the MM2 force field is used to clean up the geometry of compound 12.

Orbitals generated using MOPAC/PM6 method

HOMO

HOMO-1

LUMO

LUMO+1

LUMO+2

Orbitals generated using MOPAC/RM1 method

HOMO

HOMO-1

LUMO

LUMO+1

LUMO+2

The MOPAC/PM6 method was then applied to provide an approximate representation of the valence-electron molecular wavefunction. The orbitals generated are pictured to the left. The HOMO is expected to be the most susceptible to electrophilic attack as it is the highest energy molecular orbital that contains electrons. It would be expected for the orbitals generated to be symmetrical as the molecule itself has a high degree of symmetry. However the orbitals generated from the MOPAC/PM6 method do not represent this. The MOPAC/RM1 method was therefore also to used to see if it resulted in any improvement. The molecular orbitals generated from this method are pictured to the right. From the images it can be seen that these are much more symmetrical than the MOPAC/PM6 generated orbitals and therefore more useful in this discussion. Comparing the corresponding MOs generated by each method there appears to be a good resemblance between most. The most obvious difference is between the LUMO and LUMO+1 MOs for each method. The LUMO from the RM1 method closely resembles the LUMO+1 from the PM6 method and vice versa. However, since the HOMO is the most important orbital for determining susceptibility to nucleophilic attack these differences are not relevant. Both HOMOs generated agree that the double bond closest to the Cl (syn) is the most nucleophilic as it can be seen that it has the most electron density in the HOMO.

Compound 12 and its dihydro derivative 13 were both subjected to the B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation. This enabled the main Cl-C stretching frequency to be identified as well as the C=C bond stretching frequencies.

For Compound 12 these were:

C-Cl bond stretch 771cm^-1

C=C bond (anti) stretch 1737cm^-1

C=C bond (syn) stretch 1757cm^-1

For the dihydro derivative 13 these were:

C-Cl bond stretch 775cm^-1

C=C bond (syn)stretch 1758cm^-1

The C=C bond close (syn) to the Cl group has a significantly higher stretching frequency than the C=C bond anti to the Cl. In the monoalkene, the C-Cl bond stretch is at a higher frequency indicating a stronger C-Cl bond with greater electron density.

Monosaccharide Chemistry: Glycosidation

Caption

In a glycosidation reaction neighbouring group effects can be crucial in determining which anomer is formed. In Cation A, R=H the acetyl group is pointing down from the plane of the ring, whereas in Cation B, R=H it is pointing down.

These conformations were minimised in energy using both the MM2 force field and the MOPAC/PM6 method. Of these the MOPAC/PM6 method is expected to give a better result as it takes into account the orbital interactions whereas MM2 is unable to do this. It is a semi-empirical method. This is important for working with biological molecules as orbital interactions can define the ways in which the molecules react. In sugars such as those examined here, the anomeric effect is crucial to deciding the diastereospecificity of glycosidation reactions. In this investigation the energies of molecules A and B were minimised with both MM2 and MOPAC/PM6 and two different conformers found. The energies were investigated when R=H and R=Me. Cation A, R=H and Cation B, R=H have the acetyl group orientated with the carbonyl pointed towards the oxonium oxygen while Cation A', R=H and Cation B', R=H have the acetyl carbonyl pointing away from the oxonium oxygen. From both MM2 and MOPAC the energy of A and B are found to be lower than those of A' and B' with both R=H and R=Me (see table below). This is expected as there is a stabilising interaction between a lone pair on the carbonyl oxygen and the empty orbital on the oxonium oxygen in the cases of A and B which is absent in A' and B'.

	R=H			R=Me
	MM2 / kJmol-1	MOPAC/PM6 / kJmol-1	Difference in energy between conformers / kJmol-1 MOPAC/PM6	MM2 / kJmol-1	MOPAC/PM6 / kJmol-1	Difference in energy between conformers / kJmol-1 MOPAC/PM6
A	15.02	-401.54	52.76	132.93	-383.51	100.25
A'	63.76	-348.78		159.91	-283.26
B	37.36	-394.13	98.87	129.20	-383.42	97.95
B'	63.72	-295.26		140.83	-285.47
C	52.26	-411.29	97.03	-	-	-
C'	111.50	-314.26		-	-
D	60.96	-394.13	95.77	-	-	-
D'	108.03	-298.36		-	-

Intermediate cations C and D are obtained by the attack of the carbonyl oxygen in A and B on the oxonium ion. This results in a joined 5-membered and 6-membered ring structure. Again there are two possible isomers of C and D. When the carbonyl from cation A attacks, it will approach from the bottom face of the ring and therefore form a structure where the 5-membered ring is perpendicular to the 6-membered ring. This is . When the carbonyl from cation A' attacks it attacks from the top face resulting in a twisted structure with the 5-and 6-membered rings in a similar plane forming . A similar mechanism starting from B and B' results in and respectively.

Looking at the table above, again it can be seen that C' and D' are both higher in energy than C and D. The energies of A and C compared, gives the stabilisation energy due to the neighbouring group effect. This can be calculated to be 9.75kJmol^-1. Similarly it should be possible to do the same for B and D however, from the energy calculations I obtained it seems that they both had the same energy. This is not expected however it did not seem possible to further minimise the energy for cation D.

	MM2		MOPAC/PM6		MM2		MOPAC/PM6
	C-C-O	O-C-O	C-C-O	O-C-O	C-O	C-O	C-O	C-O
C	109o	115o	106o	106o	1.4A	1.4A|align="center"	1.5A	1.6A
C'	121o	121o	121o	112o	1.4A	1.4A	1.5A	1.5A
D	110o	117o	105o	106o	1.4A	1.4A	1.5A	1.6A
D'	122o	123o	123o	112o	1.4A	1.4A	1.5A	1.5A

The resulting bond angles and bond lengths obtained from the MM" force field and the MOPAC/PM6 method were recorded (see table), and compared. The MM2 method generally resulted in larger bond angles between the 6-membered and 5-membered ring. It also gave C-O bond lengths of 1.4A that were consistent throughout all four isomers. This also highlights the deficiencies of the MM2 method, as it is designed to fit the geometry of the molecules to known parameters for bond length and angle.

Structure Based Mini Project Using DFT-Based Molecular Orbital Methods

Stereoselective dissolving metal reductions

Caption

In a recent synthesis of (-)-4-epiaxinyssamine

, cycloketone 5 was reduced with complete stereoselectivity to give alcohol 6.

Caption

In theory a reductuion could have resulted in two products as was the case in this NaBH₄ of the same cycloketone. So why is the dissolving metal reduction stereospecific?

The structures were initially optimised by the MM2 force field then optimised using the DFT=MPW1PW91 method. Following the MM2 minimisation, the initial cycloketone 5 was found to have an energy of 110.5kJmol^-1 while 6 had energy of 109.0kJmol^-1 and 7 had an energy of 96.4kJmol^-1.

Product 6

Product 7

The ¹³C NMR spectra f both 6 (DOI:10042/to-9508 ) and 7 (DOI:10042/to-9507 ) were calculated after energy minimisation. These are shown in the table below and compared with the literature values. The C-atoms are numbered according to the results of the geometry optimisation calculations.

Compound 6					Compound 7
Calculated δ(ppm)	Literature 1 δ(ppm)	Literature 2 δ(ppm)	C assignment of δ		Calculated δ(ppm)	Literature 1 δ(ppm)	Literature 2 δ(ppm)	C assignment of δ
CDCl3	Bruker Avance 500 spectrometer 125MHz CDCl3	Varian Gemini-200 spectrometer 50MHz CDCl3			CDCl3	Bruker Avance 500 spectrometer 125MHz CDCl3	Varian Gemini-200 spectrometer 50MHz CDCl3
152.9	147.11	147.03	C-12		144.91	-	146.95	C-12
110.9	110.67	110.61	C-13		110.75	-	110.77	C-13
75.2	76.86	76.77	C-2		71.74	-	72.29	C-2
44.9	43.22	43.17	C-4		41.86	-	39.17	C-8
41.3	39.93	39.89	C-3		39.61	-	37.62	C-4
40.9	39.19	39.13	C-8		37.96	-	37.23	C-10
40.8	38.88	38.84	C-6		37.02	-	35.5	C-3
38.9	37.1	37.06	C-10		36.95	-	35.27	C-6
36.5	33.78	33.71	C-7		35.79	-	34.04	C-5
35.3	30.92	30.87	C-5		30.45	-	29.01	C-1
30.7	26.05	26.01	C-1		28.23	-	25.9	C-7
26.6	23.08	23.04	C-16		25.15	-	23.28	C-9
24.4	22.82	22.77	C-9		24.65	-	22.81	C-16
19.2	16.68	16.63	C-15		18.64	-	15.85	C-14
15.9	14.87	14.83	C-14		17.47	-	15.76	C-15

In general the values calculated corresponded well with those values found in the literature. Since none of the calculated values were out by more that 5ppm, it can be concluded that the structures obtained for 6 and 7 are correct.

The ¹H NMR ³J coupling constants were also inspected for both 6 and 7.

¹H NMR for compound 6:

	Literature 1 Bruker Avance 500 spectrometer 500MHz CDCl3				Literature 2 Varian Gemini-200 spectrometer 200MHz CDCl3
	δ(ppm)	Integral	Multiplicity	J / Hz	δ(ppm)	Integral	Multiplicity	J / Hz	H assignment of δ
	0.91	1H	m	-	-	-	-	-	-
	0.92	3H	s	-	0.9	3H	s	-	He
	1	3H	d	6.5	0.97	3H	d	6.2	Ha (J calc= 6.5Hz)
	1.19	1H	m	-	-	-	-	-	-
	1.23	1H	m	-	-	-	-	-	-
	1.26	1H	m	-	-	-	-	-	-
	1.27	1H	m	-	-	-	-	-	-
	1.38	1H	ddd	13.2, 3.7, 3.7	-	-	-	-	Hg (J calc = 12.25, 3.55, 2.95Hz)
	1.48	1H	br s	-	-	-	-	-	-
	1.57	1H	m	-	-	-	-	-	-
	1.74	1H	m	-	-	-	-	-	-
	1.75	3H	s	-	1.73	3H	s	-	Hd
	1.8	1H	m	-	-	-	-	-	-
	1.8	1H	m	-	-	-	-	-	-
	1.95	1H	ddd	14.0, 2.3	-	-	-	-	-
	2.37	1H	m	-	2.33	1H	m	-	-
	3.12	1H	m	-	3.1	1H	ddd	11.0, 9.5, 5.1	Hf (J calc = 11.22, 9.78, 4.32Hz)
	4.82	1H	br s	-	4.8	1H	m		Hb/Hc
	4.92	1H	br s	-	4.9	1H	m		Hb/Hc

¹H NMR for compound 7:

Literature 2 Varian Gemini-200 spectrometer 200MHz CDCl3	'	'	'	'
δ(ppm)	Integral	Multiplicity	J / Hz	H assignment of δ
0.89	3H	s	-	He
0.93	3H	d	6.3	Ha (J calc= 6.4Hz)
1.73	3H	s	-	Hd
2.34	1H	m	-	-
3.76	1H	m	-	Hf
4.83	1H	m	-	Hb/Hc
4.90	1H	m	-	Hb/Hc

Literature 2 only gives the most significant H NMR peaks as most are simply cyclohexane ring H with no relevance to the different stereoisomers. The three methyl peaks are obvious as they were the only ones with an integral of 3H. The two olefin H have slightly different chemical shifts as they are in different chemical environments with no free rotation possible around the C=C bond. There seems to be very little difference in the chemical shift values for the two stereoisomers. The largest difference is in the value that is assigned to Hf, which neighbours the -OH group. This seems reasonable as it is the only one that is in a different position between the two isomers. Also, in compound 6 the peak is reported in literature to be ddd while in compound 7 it is a multiplet.

The IR spectra of both stereoisomers were also calculated and compared to the literature. The most characteristic stretches for these molecules are the C=C double bond stretch and the O-H stretch. The literature values for compound 6 gave the C=C stretch as 1640cm^-1 and the O-H stretch as 3620.6cm^-1. The computed values found were 1717cm^-1 for C=C and 3834cm^-1 for O-H. In both cases the computed values were significantly higher. For compound 7 the literature values were 3416cm^-1 for O-H and 1642cm^-1 for C=C. The calculated values were 3816cm^-1 and 1720cm^-1 respectively. This deviation from the experimental result may be due to systematic errors generated from the method used to do the calculation. The deviations are between 4 and 11% of the experimental values, although they are expected to be around 8% out in general.

The IR calculations also gives a value for the free energies of the two molecules. For 6 and 7 these proved to be almost identical being -662.161 and -662.160 Hartrees. This shows there is very little difference between the molecules.

The only method really suitable for telling the two apart is the optical rotation, as the two molecules differ only in the geometry at one chiral centre, and as already seen the IR and NMR spectra are very similar. The literature value for 6 is given as [α]<sup2D=+19.7^o and that for 7 is [α]<sup2D=-16.3^o. The two values are opposite in sign as they rotate light in opposite directions. The computed values obtained were [α]<sup2D=+141.6^o for 6 and [α]<sup2D=-65.9^o for 7. Although the values do not agree, the signs do which clearly indicates the direction of light rotation.