Rep:Mod:mtr09mod1
3rd Year Computational Chemistry Project - Matthew Reynolds
Module 1: Structure and Spectroscopy
The Hydrogenation of Cyclopentadiene Dimer
Dimerisation
Cyclopentadiene can undergo a dimerisation reaction at room temperature. This dimerisation is a [4+2] cycloaddition (Diels-Alder) reaction between two cyclopentadiene units. The reaction can proceed via one of two transition states to produce a mixture of two conformational isomers, the Exo- and the Endo- form.
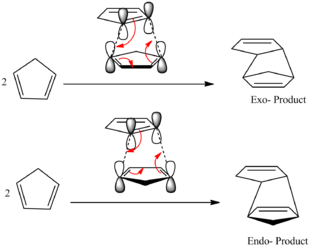
The mechanism of the reaction for both isomers is shown to the left.
In determination of the predominant form of the product, the kinetics and thermodynamics of this reaction must be considered.
Both molecules were produced on ChemBio3D, and their energies minimised through geometry optimisation by running Allinger MM2 force field calculations over their structure. The Molecular Mechanics code employed works by considering the energies of five interactions (diatomic bond stretches, triatomic bond angles, tetra-atomic bond torsions, electrostatic attractions and Van der Waals repulsions) and calculating the sum of these interactions to produce a value for 'Total Energy'.
It should be noted that the resultant parameter of 'Total Energy', when taken on it's own, is meaningless. (A comparison of this quantity can be drawn between values of 1NMR shifts when not compared against a TMS standard). Instead, we can use the difference in these values between the two isomers to obtain quantifiable results. We are able to take the difference in values of total energy between the isomers, as they were both run on the same program.
Below is a table summarising the the results from the energy minimisation for each parameter.
| Energy Type | Exo- Form (kcal mol-1) | Endo- Form (kcal mol-1) | Difference (Exo-Endo) (kcal mol-1) |
|---|---|---|---|
| Stretch | 1.29 | 1.25 | 0.04 |
| Bend | 20.58 | 20.85 | -0.27 |
| Stretch-Bend | -0.84 | -0.84 | 0.00 |
| Torsion | 7.67 | 9.51 | -1.84 |
| Non-1,4 VDW | -1.42 | -1.54 | 0.12 |
| 1,4 VDW | 4.23 | 4.32 | -0.09 |
| Dipole/Dipole | 0.38 | 0.45 | -0.07 |
| Total Energy | 31.88 | 34.00 | -2.12 |
From these calculations, it can be seen that the thermodynamic product is the Exo- form of the dimer, as it has a lower value of total energy in comparison to the Endo- form (ΔE = -2.12kcal mol-1). However, the literature[1] claims that the Endo- form is the predominant isomer found from this reaction at room temperature. Furthermore, Lenz et al. claim that when the temperature of the reaction is raised to between 425K and about 475K both isomers are formed almost equally. This would strongly indicate that the reaction is under kinetic control. It was shown by Woodward and Hoffmann (1969)[2] that analysis of the transition state would show a favourable orbital interaction between the two rings in the Endo- form, not present in the Exo- form. This would result in a lower energy transition state for the Endo- form, which would imply that more of the Endo- product forms at a greater rate.
The calculations that have been performed make the assumption that no further Diels Alder reactions take place on either the Endo- or the Exo- form of dicyclopentadiene to form tricyclopentadiene or higher molecules. It is stated by A. Turnbull and H. Hull (1968)[3] that the expected products of these further cycloadditions are thermodynamically more stable than either the Endo- or the Exo- isomer of dicyclopentadiene, however, due to kinetic factors these products are not formed with appreciable yields, and can be discounted as reaction products.
The largest difference in energy between both the isomers is in the torsional strain. The Exo- isomer has a more favourable staggered conformation along the newly formed C-C bond in comparison to the Endo- form. This results in a lack of stearic clash between the hydrogens, therefore producing a lower value of energy from the MM2 calculations, which leads it to being classed as the thermodynamic product.
However, these calculations provide no information regarding the relative energies of the transition states, therefore the kinetics of these reactions cannot be analysed using this method.
Hydrogenation
The hydrogenation of dimerised cyclopentadiene yields two possible products, Product 3 and Product 4 depending on which C=C bond is hydrogenated.

MM2 calculations were run, as before, on both the products of hydrogenation to determine which is the most likely to form. The results of these calculations are shown below:
| Energy Type | Product C (kcal mol-1) | Product D (kcal mol-1) | Difference (C-D) (kcal mol-1) |
|---|---|---|---|
| Stretch | 1.28 | 1.10 | 0.18 |
| Bend | 19.86 | 14.52 | 5.34 |
| Stretch-Bend | -0.84 | -0.55 | -0.29 |
| Torsion | 10.81 | 12.50 | -1.69 |
| Non-1,4 VDW | -1.23 | -1.07 | -0.16 |
| 1,4 VDW | 5.63 | 4.51 | 1.12 |
| Dipole/Dipole | 0.16 | 0.14 | 0.02 |
| Total Energy | 35.69 | 31.15 | 4.54 |
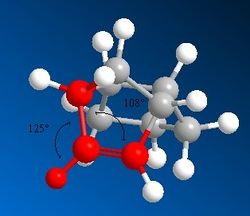
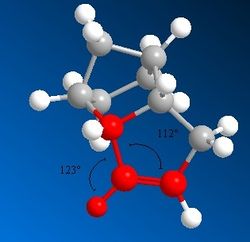
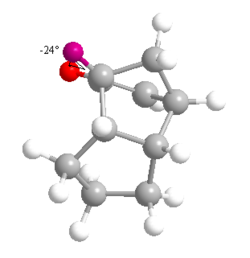
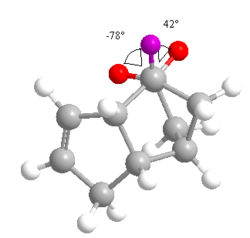
From these results, it can clearly be seen that Product 4 is lower in 'Total Energy' than Product 3, making it the thermodynamic product. Product 4 is the result of the hydrogenation of the C=C bond within the same 5-membered ring as the hydrocarbon bridge. The difference in values of energy for the bending and torsional motions and the 1,4 Van der Waals contacts in particular are quite significant. Product 4 is under less stearic strain than Product 3, as shown from the measurement of the dihedral angle shown to the left and right. It should be noted that these unfavourable stearic clashes also occur on the other side of the molecule.
There is also a large discrepancy in the bending strain between the two molecules. Molecule 4 has the lower bending energy, this can be rationalised by looking at the bond angles between the alkene bond, the attached hydrogen and the attached C-C bond (shown in Figure 3 and Figure 4). The ideal bond angle around this sp2 carbon centre is 120o, deviations from this value cause an increase in energy. Molecule 4 has less deviation [123o, 112o] from the ideal bond angle than Molecule 3 [125o, 108o].
Please note that the images of both products are viewed along the C-C bond connecting the three carbon bridge and the the site of unsaturation in the Endo- isomer of dimerised cyclopentadiene.
The conformation of the hydrogens about this bond is clearly far more staggered for Product 4 (θ = 78o and 42o) than for Product 3 (θ = 24o). This results in an energetically more favourable situation, as there is less of a stearic clash between the two adjacent hydrogens. It should be noted that Product 3 has no way of alleviating the strained hydrogen arrangement. The nature of the bridgehead and the alkene force the hydrogens to remain in this unfavourable position.
However, hydrogenating at the C=C bond opposite the bridge would release the strain within the molecule (as this =C-H bond is conformationally locked with respect to the other =C-H bond further away from the three carbon bridge).
The conformation about the C=C bond in Molecule 4 (the C=C bond that is hydrogenated to form Molecule 3) is not as unfavourable as the conformation about the C=C bond in Molecule 3, as the hydrogens connected to the C=C bond in Molecule 4 are conformationally locked in a favourable staggered position with the hydrogen attached to the molecule by a wedged bond.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Taxol is a vital drug in the treatment of Kaposi's sarcoma[4] A key intermediate in the synthesis of this natural product has two different conformers, shown below. Molecule 9 has the carbonyl group pointing up, with respect to the cyclohexane ring, whilst Molecule 10 has the carbonyl group pointing down with respect to the cyclohexane ring. 3D representations of the intermediates are provided by clicking on the names of each molecule.
ChemDraw structures of both the intermediates are shown below:
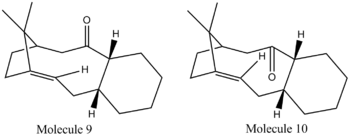
As before, both molecules were produced on ChemBio3D, and their energies minimised through geometry optimisation by running Allinger MM2 force field calculations over their structure. These calculations were to be used to determine the most thermodynamically stable intermediate.
Care was taken to ensure that the cyclohexane part of the intermediates were drawn in chair conformation. It is reported[5] that there is a difference in energy of about 5.5 kcal mol-1 between the chair and the boat form of cyclohexane.
The results of the energy minimisation are shown below:
| Energy Type | Molecule 9 (kcal mol-1) | Molecule 10 (kcal mol-1) | Difference (9-10) (kcal mol-1) |
|---|---|---|---|
| Stretch | 2.78 | 2.62 | 0.16 |
| Bend | 16.54 | 11.34 | 5.20 |
| Stretch-Bend | 0.43 | 0.34 | 0.09 |
| Torsion | 18.25 | 19.67 | -1.42 |
| Non-1,4 VDW | -1.55 | -2.16 | 0.61 |
| 1,4 VDW | 13.11 | 12.87 | 0.24 |
| Dipole/Dipole | -1.72 | -2.00 | 0.28 |
| Total Energy | 47.84 | 42.68 | 5.16 |
Merck Molecular Force Field 94 (MMFF94) calculations were also run on both of these structures, to produce alternate values of 'Total Energy'. MMFF94 calculations are generally more sophisticated than the corresponding MM2 calculations. The most important difference between MMFF94 and the MM2 occurs in the analysis of non-bonded interactions[6]. The MMFF94 calculations treats intermolecular and intramolecular interactions in the same electrostatic way. MM2, on the other hand, would treat hydrogen bonds as a mere defined stabilisation of energy using the Van der Waals contact equation.
| Energy Type | Molecule 9 (kcal mol-1) | Molecule 10 (kcal mol-1) | Difference (9-10) (kcal mol-1) |
|---|---|---|---|
| Total Energy | 70.53 | 60.54 | 9.99 |
Performing the MMFF94 calculation did not drastically alter the geometry of the intermediate (as will be seen when optimisation is performed using semi-empirical methods such as MOPAC/PF6 in Questions 3 and 4), which has been optimised by the MM2 calculation prior to this. This shows that, although MMFF94 takes more interactions into account, MM2 calculations suffice in providing a reasonably accurate geometrical optimisation.
From both sets of data it can clearly be seen that Molecule 10, the intermediate in which the carbonyl group is pointing downwards, is the more thermodynamically stable conformer. There are multiple factors affecting the stability of the two intermediates. From the MM2 calculations, it is evident that the difference in triatomic bending motions is the largest factor in determining the thermodynamic stability of the two intermediates. From assessment of the 3D structures, it can be seen that in Molecule 10, the carbonyl group is in an antiperiplanar arrangement with respect to two of the adjacent three hydrogens. For Molecule 9, this antiperiplanar relation is lost, and replaced by a highly unfavourable synperiplanar arrangement. The unfavourable nature of these interactions causes Molecule 9 to undergo isomerisation to form Molecule 10.[7]
This intermediate also provides a good example of a hyperstable alkene. This phenomena is observed when a molecule has an unsaturated C=C bond to a bridgehead carbon. As the ring size decreases, the strain involved in the C=C bridgehead bond becomes greater. This strain is relieved with increasing ring size (very large rings effectively have allyic alkene bonds). However, for intermediate ring sizes the C=C bridgehead bond becomes incredibly stable. Due to this increased stability, the C=C bond would be expected to react slowly to hydrogenation/halogenation reactions. J-S Kim (1996) reports that this phenomena is not due to stearic hinderance nor the energy of the p-bonds.[8]
An MM2 energy minimisation has been performed on the product of the hydrogenation reaction of Molecule 10, with the results shown below:
| Energy Type | Hydrogenation Product (kcal mol-1) |
|---|---|
| Stretch | 2.71 |
| Bend | 18.84 |
| Stretch-Bend | 0.59 |
| Torsion | 20.23 |
| Non-1,4 VDW | -2.18 |
| 1,4 VDW | 16.19 |
| Dipole/Dipole | -1.75 |
| Total Energy | 54.63 |
The value of total energy is lower for the hydrogenated product than for the its alkene precursor (Molecule 10). This is in agreement with the literature, which stated that the hydrogentation reaction across the hyperstable double bond would be slow. The 'new' hydrogen inserted onto the cyclopentane ring is locked, by virtue of the carbon bridge, into a synperiplanar conformation with respect to one of the methyl groups on the top of the cyclopentane ring. This would explain the far larger value of energy for the bending energy in the hydrogenated product when compared to the unsaturated form, which would explain why there is such a drastic increase in 'Total Energy'.
An MMFF94 calculation was also performed on this structure, after optimisation with the MM2 Force Field option. This yielded a total energy of 77.39kcalmol-1.
Regioselective Addition of Dichlorocarbene
The aim of this section is to show the alternate uses of computational analysis, in particular, the computing of Molecular Orbitals (MO's) on molecules, and using the results to predict the reactivity of certain molecules. In this example, the Molecular Orbitals of Molecule 12 have been calculated in an attempt to predict the site of reactivity upon electrophillic attack from dichlorocarbene.
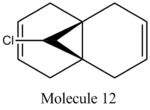
Prior to this, the energy of the system was minimised using MM2 calculations, with the results shown below:
| Energy Type | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Dipole/Dipole | Total Energy |
|---|---|---|---|---|---|---|---|---|
| Molecule 12 (kcal mol-1) | 0.62 | 4.74 | 0.04 | 7.65 | -1.07 | 5.79 | 0.11 | 17.89 |
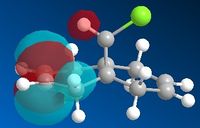
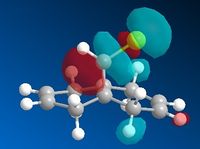
The molecular orbitals were subsequently calculated for Molecule 12 using the MOPAC/PM6 MO method provided by the ChemBio3D software. This method approximates the valence electron wavefunctions for the molecule under consideration.[9] The five most relevant Molecular orbitals (HOMO -1, HOMO, LUMO, LUMO + 1 and LUMO + 2) to the aforementioned reaction are shown below.
Upon inspection, most of the molecular orbitals are in agreement with the molecular point group of the molecule, Cs [Symmetry Elements: E, σh]. There seems to be a general plane of symmetry bisecting the centre of each MO, which would be in agreement with the molecular point group. However, this is only a general observation, the MO's are not strictly symmetrical.
Furthermore, it can also be seen that the number of stronger, bonding interactions decreases as you move from the HOMO -1 MO to the LUMO +2 MO. Both of the C=C bonds have strongly bonding MO's situated on them at the HOMO -1 level. Whereas, at the LUMO + 2 level, the Endo- C=C bond has a strongly antibonding orbital situated on it, whilst a non-bonding interaction is observed on the Exo- C=C bond. This is also in agreement with the general trend that, as you increase in energy, you increase the number of antibonding interactions.
When considering the reactivity of the diene towards electrophiles, it is obvious that the Highest Occupied Molecular Orbital (HOMO) should be the primary orbital considered (as the electrons situated within this MO will attack the electrophillic chlorocarbene species). Upon inspection of the HOMO, it can be seen that a large amount of electron density is situated on the C=C bond, which is in the Endo- position with respect to the Cl atom on the bridge. This observation is in agreement with the article by Rzepa et al. (1992), in which it was found that the Endo- C=C bond was rendered more nucleophillic due to a stabilising antiperiplanar interaction between the Cl-C σ* orbital and the Exo- π-orbital.[10]
The second part of this question requires the prediction of the Infrared spectra of both Molecule 12 and its mono-hydrogenated product using Gaussview 5.0 software.
The geometries of both Molecule 12 and its monohydrogenation product (henceforth known as Molecule 13, shown to the left) were optimised using MM2 and MOPAC/PM6 calculations. The results of the MM2 calculations for Molecule 12 has already been reported. The MOPAC/PM6 calculation determined the heat of formation for Molecule 12 to be 19.74kcal mol-1.
The results of the geometry optimisations are shown below:
| Energy Type | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Dipole/Dipole | Total Energy |
|---|---|---|---|---|---|---|---|---|
| Molecule 13 (kcal mol-1) | 0.90 | 4.69 | 0.01 | 10.76 | -1.07 | 6.97 | 0.07 | 22.34 |

The MOPAC/PM6 calculation determined the heat of formation to be -2.43kcalmol-1. Upon optimisation, it was noted that the saturated ring became slightly more bent, in comparison to the geometry that was observed when the MM2 Force Field calculations were run.
It was suggested previously that the Endo- C=C bond was more nucleophillic than the Exo- C=C due to stablising interaction between the Cl-C σ* antibonding orbital and the Exo- π orbital. If this were to be the case, it would be expected that the frequency of vibration for the Exo- C=C bond would be lower than that of the Endo- C=C vibration, due to the weakening of the Exo- C=C bond from the donation of electron density from the π system into the C-Cl antibonding orbital.
The relationship between bond strength and vibrational frequency is given by the Simple Harmonic Oscillator equation: ν = (1/2π)*(k/μ)0.5, which indicates frequency decreases with decreasing bond strength (represented by the force constant, k).
The IR spectrum obtained for Molecule 12 is shown below[11]:

The following stretching modes were found using the Gaussview software: Exo-C=C: 1737.1cm-1 Endo-C=C: 1757.4cm-1 C-Cl Stretch: 770.9cm-1. It is clear from the frequencies of vibration for the C=C bonds that the Exo- bond is weaker than its Endo- equivalent. This is in agreement with the expected results stated previously.
The IR spectrum obtained from the SCAN system calculations for Molecule 13 is shown below[12]:

The following stretching modes were found using the Gaussview software: Endo-C=C: 1758.1cm-1, C-Cl Stretch: 774.9cm-1. The most obvious difference between both the IR spectra is the lack of a second C=C stretching mode (corresponding to the Exo- C=C stretch). However, the most informative of piece of data obtained from these spectra is the shift in the C-Cl stretching frequency for the Mono-alkene product. This stretching mode occurs at a higher frequency in the mono-alkene product than for the di-alkene precursor. In Molecule 13 there is no donation of electron density into the C-Cl σ* orbital, meaning the bond order is not reduced, signifying a stronger bond is formed.
Monosaccharide Chemistry: Glycosidation
The aim of this section is to demonstrate how computational chemistry can be used to rationalise the effect of neighbouring group participation during a glycosidation reaction. A glycoside is typically formed when a leaving group, in this case 'X', is substituted by an incoming nucleophile, 'Nu-'. However, this glycoside can occur as one of two possible conformers, depending on the orientation of the acetyl group adjacent to the anomeric centre. This is all dependent on the stablisation of the intermediate oxonium ion through electron donation by the adjacent acetyl group. If the acetyl group is in an axial position, then the α- anomer, in which the glycosidic bond is also axial, is almost exclusively formed. However, if the acetyl group is in an equatorial position, then the β- anomer is normally observed.[13] This observation is summarised by the figure below:

The oxonium intermediate will be analysed using both MM2 and MOPAC/PM6 methods to rationalise the stereospecific nature of the glycoside formation.
MM2 analysis is used beforehand to perform a crude energy minimisation, and also to optimise the geometry of the molecule. Once this is complete, the MOPAC/PM6 program can perform a further energy minimisation, as this code takes into account more interactions within the molecule, in particular orbital interactions (as stated in the previous section). The disparity between methods is evident for larger systems, such as the ones we are currently analysing, as there are far more intramolecular interactions to be considered.
Prior to calculation, however, a suitable 'R' group must be chosen for all the non-Acetyl alcohol groups. This 'R' group cannot be too big, otherwise local minima, as opposed to global minima would be more likely to be found as a result of the energy minimisation, as there would be far more bond rotations to consider. Furthermore, increasing the size of the group, or introducing a heteroatom would increase the number of energy interactions within the molecule for the MM2/MOPAC code to take into account. The simplest possible 'R' group to chose for this system is therefore a methyl group.
Representations of the two oxonium ions under consideration are shown below:
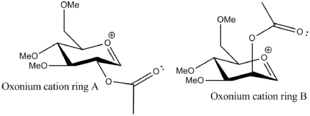
As mentioned prior to this, the acetyl group can attack from an equatorial position above the ring (A), an equatorial position below the ring (A'), an axial position above the ring (B) or an axial position below the ring (B'). The MM2 calculation was performed to optimise the geometry of four different conformations of the oxonium ion.
The results of the geometry optimisation using the MM2 Force Field calculation is shown below, only the value for 'total energy' is shown:
| Energy Type | Attack from above (A) (kcal mol-1) | Attack from below (A') (kcal mol-1) | Difference (A-A') (kcal mol-1) |
|---|---|---|---|
| Total Energy | 33.34 | 20.02 | 13.32 |
| Energy Type | Attack from above (B) (kcal mol-1) | Attack from below (B') (kcal mol-1) | Difference (B-B') (kcal mol-1) |
|---|---|---|---|
| Total Energy | 24.24 | 32.31 | -8.07 |
The preliminary MM2 Force Field calculations strongly suggest that, for the equatorial conformer, attack from below the plane of the ring is energetically more favourable. On the other hand, for the axial conformer, attack from above the plane of the ring is energetically more favourable.
MOPAC calculations were then run on all four conformers, to further optimise the geometry by taking into account orbital interactions. This software also determines the heat of formation/kcal mol-1 for each of the conformers. between The resultant opitmised structures are shown in the links below:
MOPAC-optimised structure of conformer A | MOPAC-optimised structure of conformer A' | MOPAC-optimised structure of conformer B | MOPAC-optimised structure of conformer B'
The determined parameter 'heat of formation', which is a far more accurate description of 'total energy' within the system, for each conformer is shown in Table 11 below:
| Energy Type | Attack from above (axial) (B) | Attack from below (axial) (B') | Attack from above (equatorial) (A) | Attack from below (equatorial) (A') |
|---|---|---|---|---|
| Heat of Formation (kcal mol-1) | -90.51 | -91.58* | -85.00* | -89.24 |
Note: Upon optimisation of B' and A, it was noted that the MOPAC/PM6 program distorted the geometry of these structures to such a extent that, for B', the final conformation was almost indistinguishable from that of B, hence the apparent 'closeness' in energy of formation. For conformer A, the carbonyl group was rotated about the C-C bond to the other side of the six membered ring, so that it was pointing away from the oxonium cation, this is shown more clearly when the interatomic distances between the carbonyl oxygen and the oxonium carbon are determined (see Table 12). This conformation can no longer be classed as 'attacking the ion from above the plane of the ring in an equatorial position'.
However, these 'anomalous' results have demonstrated exactly how unfavourable these two conformations (A and B') are, with respect to A' and B. The values of 'heat of formation' for both of the conformations which were determined energetically favourable by the MM2 Force Field calculations were large and negative, which is in agreement with the results of further analysis into intramolecular interactions within these conformers by the MOPAC/PM6 method, where both conformations remain the energetically more favourable mode of attack. This is an example of diastereospecificity.
However, it was noted that the MOPAC optimisation forced the attacking oxygen atom closer to the oxonium δ+ carbon atom. The post-optimisation interatomic distances between the oxygen atom of the attacking carbonyl group and the δ+ carbon atom of the oxonium group were determined for each structure. The results of these distance determinations are illustrated in Table 12, (below):
A very important observation relating to the optimisation method has be shown in these results. Disregarding the result for conformer A, the interatomic distances between the carbonyl oxygen atom and the oxonium carbon atom are lower than the sum of the Van der Waals radii of oxygen and carbon (1.52A + 1.70A = 3.32A)[14]. This phenomenon can be explained by considering how the MOPAC/PM6 calculation performs geometry optimisation.
When optimising with the MM2 Force Field software, the stereochemistry around each individual atom is preserved as drawn. However, the MOPAC optimisation program disregards the rigid bonds drawn on the ChemBio3D program, and can, in effect, produce its own implicit bonds during geometrical optimisation. It is likely that the optimisation software has produced the aforementioned 'implicit bonds' between these two atoms.
It is also interesting to note that the angle between the carbonyl oxygen and the oxonium ion seems to be in the region of 110o > θ > 100o, (Note: ChemBio3D cannot determine the angles between 'non-bonded' atoms) which is close to the Bürgi-Dunitz trajectory [the angle at which maximum orbital overlap with the π* system is achieved, but the repulsion from the filled π orbital is minimised] for Nucleophillic attack on carbonyls.[15]
This implicit 'bond' that the MOPAC/PM6 method has determined to be present during energy minimisation will be studied further through analysis of the intermediates of the glycosidation reaction, where the two atoms in question are connected by a rigid bond. The same procedure of energy minimisation as before was employed on these structures, shown below.

Not present in the above diagram are the structures of C' and D', which are formed by the attack of the carbonyl group from below the plane of the ring by species A' and B' respectively. MM2 Force Field calculations were performed on the molecules to optimise their geometries, the results of which can be seen by following the links provided:
MM2 structure of intermediate C | MM2 structure of intermediate C' | MM2 structure of intermediate D | MM2 structure of intermediate D'
As with the previous four conformations of A and B, the tabulated values of total energy for all four conformations of intermediates C and D are shown below:
| Energy Type | Attack from above (C) (kcal mol-1) | Attack from below (C') (kcal mol-1) | Difference (C-C') (kcal mol-1) |
|---|---|---|---|
| Total Energy | 48.02 | 41.24 | 6.78 |
| Energy Type | Attack from above (D) (kcal mol-1) | Attack from below (D') (kcal mol-1) | Difference (D-D') (kcal mol-1) |
|---|---|---|---|
| Total Energy | 40.11 | 44.98 | -4.87 |
The four intermediates were subsequently optimised using the MOPAC/PM6 method. The following structures were obtained:
MOPAC structure of intermediate C | MOPAC structure of intermediate C' | MOPAC structure of intermediate D | MOPAC structure of intermediate D'
The energy of formation values for each of the intermediates are tabulated below:
| Energy Type | Attack from above (axial) (D) (kcal mol-1) | Attack from below (axial) (D') (kcal mol-1) | Attack from above (equatorial) (C) (kcal mol-1) | Attack from below (equatorial) (C') (kcal mol-1) |
|---|---|---|---|---|
| Heat of Formation | -90.51 | -66.48 | -66.87 | -91.66 |
These results clearly indicate that C' and D are the more favourable conformations of the intermediates in the glycosidation. The large discrepancy in 'heats of formation' between the conformations is a further demonstration of the diastereospecificity of this reaction. The results of the MOPAC/PM6 calculations on these intermediates is also in agreement with the results of the same calculations on the oxonium precursors, which determined that conformations A' and B (the respective precursors to C' and D) are more favourable than A and B'.
Upon closer analysis, it can be seen that values of heat of formation for C' and D are almost identical to those for the their precursor conformers, A' and B respectively. This similarity in energy can be rationalised by determining the bond lengths between the Neighbouring Group oxygen and the anomeric carbon, shown below:
As mentioned previously, the MOPAC/PM6 optimisation calculation is able to create its own 'implicit' bond between the carbonyl and the oxonium carbon by taking into account the orbital contribution of each atom. A comparison of the bond lengths between the Neighbouring Group oxygen and the anomeric carbon in the intermediates C', D and D'(which are bound by a rigid bond) with the interatomic distance between the carbonyl and the oxonium carbon in the precursors A', B and B' (which can only interact in space) respectively will reveal that both distances are almost identical (1.5A for the bond, 1.6A for the interatomic distance).
It is therefore clear that the MOPAC optimisation method treats conformers A', B and B' as possessing the same structure as intermediates C', D and D' respectively.
The diastereospecificity of the glycosidation reaction can be rationalised further by determining the relative abundances of the each pair of conformers (D and D', C and C') which is done by calculating the Boltzmann distribution of each conformation. It is expected, from the large disparity in energy, that the probability of finding conformers C' and D will be far greater than that of C and D' respectively.
The equation for the Boltzmann distribution is as follows:
Ni = exp(-εi/kb*T)
Where Ni is the relative population of a particular state, with εi as its corresponding energy, kb is the Boltzmann constant (in kcal, as opposed to kJ) (3.298 x 10-27 kcal K-1) and T is the temperature at which the simulation was set (298.15 K).
The calculated relative populations of each state are shown below in Table 17 (C/C') and Table 18 (D/D'), with the relative energy for the conformer in the i = 1 state being the difference in the value of Heat of Formation between each pair of conformers, as determined by the MOPAC/PM6 software.
| Conformer + Energy state i | Relative Energy of state εi (kcal mol-1) | Relative Population of State Ni |
|---|---|---|
| C (i = 1) | 24.79 | exp(-2.5*1025) ~ 0 |
| C' (i = 0) | 0 | 1 |
| Conformer + Energy state i | Relative Energy of state εi (kcal mol-1) | Relative Population of State Ni |
|---|---|---|
| D (i = 0) | 0 | 1 |
| D' (i = i) | 24.03 | exp(-2.4*1025) ~ 0 |
The Boltzmann distribution confirms that the two most energetically favourable intermediates, C' and D, are effectively 100% abundant. This confirms the observation that the glycosidation reaction, under the regime of Neighbouring Group participation, is highly diastereospecific.
This question has shown the inherent flaw in relying solely upon Allinger MM2 calculations to optimise the geometry of larger molecules that contain several heteroatoms. By not taking electronic orbital interactions into account, the MM2 calculation only provides a basic indication as to the selective nature of the glycosidation reaction. It is only when the MOPAC/PM6 method is employed, can meaningful energies and structures be produced (Note the difference in orientation of the neighbouring acetyl group between the MM2- and the MOPAC- optimised structures).
Structure Based Mini-Project: Investigating the regioselectivity of the Baeyer-Villiger reaction
The aim of this mini project is to investigate the use of different computational techniques to characterise the regioisomeric products of the Baeyer-Villiger oxidation reaction shown in Figure 20. The Baeyer-Viliger reaction is of great use to synthetic chemists, in that it can convert a ketone group into either an ester or a lactone (from cyclic ketones). This occurs through addition of a peroxy- acid, such as mCPBA (meta- chloroperoxybenzoic acid), to the ketone which forms a species known as the 'Crigee intermediate'[16] (labelled 'Intermediate X' in the mechanism). The subsequent fragmentation of the intermediate leads to the formation of the ester/lactone product and carboxylate ion side product.
The Baeyer-Villiger reaction in question one step in the formation of acetoxyazetidinone, as described by Laurent, et al. (2004)[17]. It was found that the Baeyer Villiger oxidation of (3S, 4S, 5R)-3-(1'-Hydroxyethyl)-4-(2'-methyl-1'-oxopropyl)-azetidin-2-one [Molecule 10, in the reaction scheme below, with R = iPr] resulted in two observable products being formed, in an almost equimolar relation. (3S, 4S, 5R)-3-(1'-Hydroxyethyl)-4-(iso-Propyl oxo-methyloxy)-azetidin-2-one [Molecule 11, R = iPr] was formed from the fragmentation of Intermediate X in which the C-C bond between the azetidinone moiety and the carbonyl group undergoes a migration, whereas (3S, 4S, 5R)-3-(1'-Hydroxyethyl)-4-(iso-propyloxy-oxomethyl)-azetidin-2-one [Molecule 12, R = iPr] is formed from the same fragmentation reaction, however unlike the Molecule 11 fragmentation, the C-C bond to the iso-Propyl group is that which undergoes migration. This can rationalised by assessing the stereoelectronics of the reaction. For the fragmentation to occur the orbitals of three substituents must be in the appropriate antiperiplanar relation with each other. These antiperiplanar relations are: One of the lone pairs in the p orbital of the oxygen atom (nO) with the antibonding orbital C-C bond that is to undergo migration (σ*C-C) and the bonding orbital of the migrating C-C bond ((σC-C) with the antibonding orbital of the (weak) O-O peracid bond (σ*O-O).[18] Being that there are two possible C-C bonds that can undergo migration, a mixture of products is expected.

It was found[19] that altering the R- group attached to the carbonyl on Molecule 10 changes the selectivity of the Baeyer-Villiger reaction. The selectivites for four groups are shown below:
| R- group | Ratio 11:12 |
|---|---|
| R = Ph (b) | 100:0 |
| R = tBu (c) | 0:100 |
| R = iPr (d) | 52:48 |
| R = cPr (e) | 100:0 |
Rationalisation for the preference between Products 11 and 12 for each different R- group
As shown in Table 19 (above), the predominant configuration of the product formed from the Baeyer-Villiger oxidation is highly dependent on the attached R- group. This can be explained by discussing the migratory aptitude of each R- substituent.
Substituents which can accommodate partial positive charges are far more likely to undergo migration during the fragmentation stage of the reaction. The ability of a group to accommodate partial charge is dependent upon several factors, such as hybridisation of the carbon centre and hyperconjugation from adjacent groups. The factors affecting the regiospecificity of the four cases found in the literature are discussed below:
For the case R = Ph: The product of the Baeyer-Villiger reaction with the R- group being a Phenyl ring was exclusively regioisomer 11. During the fragmentation of Intermediate X into this regioisomer, it is the azetidinone ring which undergoes migration to form the Product molecule. The group that undergoes migration (either R- or the azetidinone ring) is the that which can best accommodate partial positive charge. In this particular case, the carbon on the Phenyl ring is sp2 hybridised, whereas the carbon on the azetidinone ring is sp3 hybridised. An increase in 's' character on a carbon centre results the contraction of the orbital radius, thereby making that carbon centre slightly more positively charged than the sp3 carbon on the azetidinone ring. It would therefore be far less energetically favourable to situate a positive charge on the sp2 carbon centre as opposed to the sp3 carbon centre. This results in 100% regioselectivity for the product that requires the migration of the sp3 carbon centre (11).
For the case R = tBu: To rationalise why the product that involves the migration of the R- group is formed almost exclusively, we must invoke the argument of hyperconjugation. The tBu tertiary carbon is more substituted than the carbon atom situated on the azetidinone ring. As a result, there are more σ bonds to methyl groups on the tBu carbon centre. The electron donating ability of these bonds results in greater stabilisation of partial positive charge for the tertiary carbon centre than for the secondary, resulting in a 100% preference for the product that requires the migration of the R- group (12).
For the case R = iPr: We can invoke the argument of hyperconjugation again to explain why there is an approximate equimolar mix of regioisomeric products. Both the carbon on the R- group and the carbon on the azetidinone ring are secondary carbons. This results in no overall preference between which group undergoes migration, hence a 50:50 mix of products is observed.
For the case R = cPr: The cyclic propyl group cannot perform hyperconjugation as effectively as the iso propyl group discussed previously, due to the locking of the three propyl carbons in a ring system. This results in a reduction of the bond angle between the three carbon atoms in the ring, thereby reducing the sp3 character of the carbon atom which would be expected to accommodate the partial positive charge. As with the Phenyl group before, this is less favourable than the sp3 azetidinone carbon accommodating the partial positive charge. This results in 100% regioselectivity for the product that requires the migration of the fully sp3 hybridised carbon centre (11).
Determining the most effective way of spectroscopically distinguishing between the two regioisomers Molecule 11 and Molecule 12
Two extremes of selectivity in this reaction (R = Phenyl and tert-Butyl) along with the product which is formed in an equimolar ratio (R = iso-Propyl) will subsequently be investigated for the determination of the most informative way to distinguish between Products 11 and 12. This is to ensure that the conclusions drawn from this analysis are applicable to more than just one individual reaction.
During this investigation, six different products of this reaction will be characterised by 13C, 15N and IR spectroscopy, subsequent analysis will determine which method is best for differentiating between the two regioisomers. 3D images of the Gaussian DFT-optimised geometry of each Product molecule are provided in the table below;
| R- group | Product Molecule 11 | Product Molecule 12 |
|---|---|---|
| R = Ph | Molecule 11b [20] | Molecule 12b [21] |
| R = tBu | Molecule 11c [22] | Molecule 12c [23] |
| R = iPr | Molecule 11d [24] | Molecule 12d [25] |
Each molecule has undergone prior energy minimisation through geometrical optimisation using both the Allinger MM2 and MOPAC/AM1 software. The results of this energy minimisation are shown below:
| Molecule | MM2 'Total Energy'/kcalmol-1 | MOPAC/AM1 'Heat of Formation'/kcalmol-1 |
|---|---|---|
| 11b | 53.69 | -111.86 |
| 11c | 50.55 | -159.26 |
| 11d | 52.52 | -152.34 |
| 12b | 48.44 | -106.73 |
| 12c | 47.51 | -159.23 |
| 12d | 46.88 | -157.40 |
Differentiating between the two regioisomers using 13C NMR Spectroscopy
The first of the three methods used to attempt to distinguish between the two regioisomers (Molecules 11 and 12) was the use of 13C NMR spectroscopy. A prediction of the 13C NMR spectrum of each compound was performed on the SCAN server using the Quantum mechanical DFT Gaussian GIAO method devised by D. Braddock & H. Rzepa (2008)[26], after optimisation of the structure with the MM2, MOPAC/AM1 and Gaussian mpw1pw91 methods.
There is an inherent issue within this method of 13C NMR predicition, though. The accuracy of the method employed is reasonably low, and that NMR shifts calculated using this method are only accurate to within 1-3ppm.[27] Furthermore, the method used is particularly inaccurate when predicting the shifts of carbonyl carbons. The predicted values of δ tend to be out by approximately 5ppm. When discussing the 13C NMR predicitions, a correction calculation has been performed on the shifts of the relevant carbons.
The carbonyl shift correction calculation is given by: δ(corr)/ppm = 0.96δ(calc) + 12.2
The accuracy of the method will be tested by comparing the calculated chemical shifts with those given in the literature for Molecules 11d and 12d. For the spectra following this, only the peaks relevant to assessing the regiospecificity of the Baeyer-Villiger reaction will be consdiered.
The predicted 13C NMR spectra for all six molecules are shown below (Figures 22 through 27).
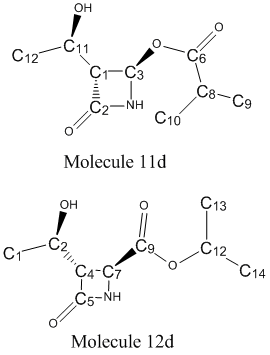
The 13C NMR for Molecule 11d is shown below, with the characterisation table shown below that [28]:

| Carbon Atom | δ(calc)/ppm | δ(corr)/ppm | δ(lit)/ppm | Difference between δ(corr) and δ(lit)/ppm |
|---|---|---|---|---|
| C1 | 67.5 | N/A | 65.2 | 2.3 |
| C2 | 157.4 | 163.3 | 167.2 | -3.9 |
| C3 | 80.2 | N/A | 75.9 | 4.3 |
| C6 | 170.4 | 175.8 | 177.6 | -1.8 |
| C8 | 32.8 | N/A | 34.0 | -1.2 |
| C9 | 20.3 | N/A | 18.9 | 1.4 |
| C10 | 19.8 | N/A | 18.8 | 1.0 |
| C11 | 66.2 | N/A | 63.9 | 2.3 |
| C12 | 22.8 | N/A | 21.3 | 1.5 |
From these results, it can be seen that the 13C NMR predicition by the GIAO Gaussian method is concordant with the values of chemical shift reported in the literature to within about 1-3ppm.[29] Even though this is within the stated error limits, this is not perfectly accurate, and suggests that this method should only be used as a general guideline in the predicition of 13C NMR shifts. This spectrum can be compared to the predicted 13C NMR spectrum of product 12d (the regioisomer of 11d), in order to identify specific carbons which differ in chemical shift by a large amount between the two regioisomeric products. These observations can then be directly compared with the results obtained from performing the same analysis on regioisomers 11b/12b and 11c/12c, in order to find a general trend for differentiating between the two product molecules 11 and 12, for any chosen R- group.
The 13C NMR for Molecule 12d is shown below, with the characterisation in corresponding table[30]:
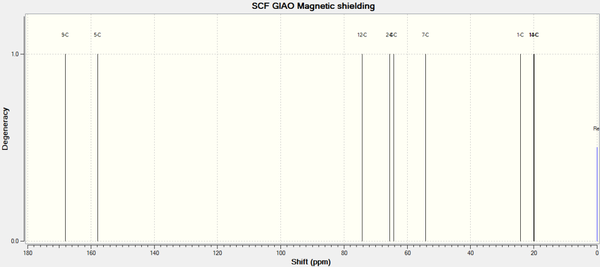
| Carbon Atom | δ(calc)/ppm | δ(corr)/ppm | δ(lit)/ppm | Difference between δ(corr) and δ(lit) /ppm |
|---|---|---|---|---|
| C1 | 24.2 | N/A | 21.9 | 2.3 |
| C2 | 65.5 | N/A | 64.5 | 1.0 |
| C4 | 64.3 | N/A | 64.0 | 0.3 |
| C5 | 157.8 | 163.7 | 168.3 | -4.6 |
| C7 | 54.3 | N/A | 50.0 | 4.3 |
| C9 | 168.1 | 173.6 | 170.8 | 2.8 |
| C12 | 74.3 | N/A | 69.7 | 4.6 |
| C13 | 19.8 | N/A | 21.3 | -1.5 |
| C14 | 20.1 | N/A | 21.8 | -1.7 |
As with the literature comparison before, the majority of the predicted shifts are within the expected error range of 1-3ppm. This demonstrates that the GIAO DFT Gaussian method is able to predict the relative positions of 13C chemical shifts for small molecules to a reasonable degree of accuracy.
Upon comparison of the 13C NMR spectra of molecules 11d and 12d, four particular carbon atoms appear to alter in chemical shift between the two regioisomers, to such a degree that their shifts could allow you to determine which one of the two regioisomers you had present as the result of the Baeyer-Villiger reaction. The carbons of interest are labelled C1, C3, C6 and C8 in Molecule 11 and C4, C7, C9 and C12 in Molecule 12. As a way to determine if this observation is applicable to the same Products 11 and 12, but with different R- groups (Ph ("b"), tBu ("c")), the 13C NMR spectra of all four of these Products (11b, 12b, 11c and 12c) has been predicted using the same method as with 11d and 12d.
The rest of the 13C NMR spectra are shown below, with the tabulated data for the relevant Carbon atoms (C1, C3, C6 and C8 for Molecule 11 and C4, C7, C9 and C12 for Molecule 12) shown below the last of the four spectra.
Predicted 13C NMR Spectrum for Molecule 11b - R- = Ph [31]
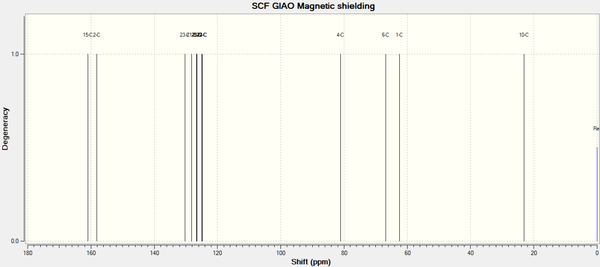
Predicted 13C NMR Spectrum for Molecule 11c - R- = tBu [32]

Predicted 13C NMR Spectrum for Molecule 12b - R- = Ph [33]
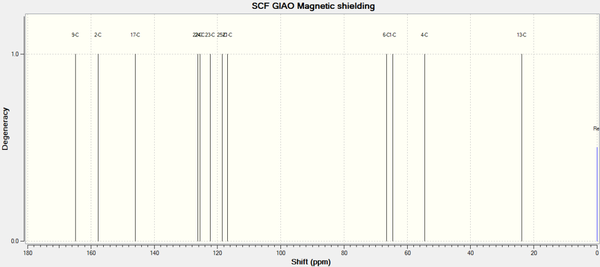
Predicted 13C NMR Spectrum for Molecule 12c - R- = tBu [34]

Please Note: The carbon numbers for Products b and c have been normalised so that they conform with the carbon numbering in Figure 21 to allow direct comparisons with Products 11d and 12d. This means that the carbon numbers presented in the following tables do not correspond exactly to those depicted on the NMR spectra above. Furthermore, carbon 8 (Molecule 11) and carbon 12 (Molecule 12) have different functionality between products b-d, so less meaningful conclusions can be drawn between species on these positions (i.e you can only directly compare carbon 8 on Molecule 11c to carbon 12 on Molecule 12c, and not to either Product groups b or d).
| Carbon Number (Molecule 11) | Corrected Chemical Shift (R=tBu)/ppm | Carbon Number (Molecule 12) | Corrected Chemical Shift (R=tBu)/ppm |
|---|---|---|---|
| C1 | 62.2 | C4 | 64.4 |
| C3 | 80.6 | C7 | 54.5 |
| C6 | 178.6 | C9 | 173.4 |
| C8 | 40.9 | C12 | 80.4 |
| Carbon Number (Molecule 11) | Corrected Chemical Shift (R= Ph)/ppm | Carbon Number (Molecule 12) | Corrected Chemical Shift (R=Ph)/ppm |
|---|---|---|---|
| C1 | 62.4 | C4 | 64.5 |
| C3 | 81.1 | C7 | 54.5 |
| C6 | 166.7 | C9 | 170.5 |
| C8 | 126.5 | C12 | 146.0 |
Immediately apparent is the large difference in chemical shift between carbon 3 and carbon 7 for both molecule groups b and c. This corresponds to the carbon situated directly above the Nitrogen atom, which is either attached to the carbonyl- end of the ester (in Molecule 11) or the oxy- end of the ester (in Molecule 12). This peak has also be shown to not vary in chemical shift all that much upon R- group substitution, meaning it can be easily identified in any 13C NMR spectrum of these products. Similar large differences are experienced by the carbon on the other side of the ester -COO- moiety C8 (in Molecule 11) and C12 (in Molecule 12). The issue with relying on this particular carbon shift to determine which of the two regioisomers is present has already been alluded to. This particular shift can appear anywhere on the 13C NMR spectrum. A perfect example of this is shown in the spectra for b and c, in which this particular carbon is found at a far higher value of chemical shift for the R- = Phenyl species, than for the R- = tBu species. This can be explained by invoking the idea of ring currents deshielding aromatic carbons. As this carbon is part of the R- group, and therefore could be attached to anything, it does not have a defined chemical shift, thereby making it ineffective as the differentiating factor when determining which regioisomer is present. Both of the other two pairs of carbon shifts do not produce a wide enough variation in the value of chemical shift to be considered effective as the deteriming factor.
Differentiating between the two regioisomers using 15N NMR Spectroscopy
Although 13C NMR spectroscopy has provided a reasonably conclusive method of differentiating between each regioisomer, it was considered that 15N NMR spectroscopy could provide an alternative pathway to differentiating between regioisomers. The main advantage of using 15N NMR spectroscopy over 13C NMR spectroscopy is the simplicity of the produced spectrum, with only one shift present, there is no possiblity of incorrectly assigning a peak. 15N NMR data obtained for each molecule is shown in the Table below. Note that, due to the difficulty in running 15N NMR spectroscopy, no literature values could be obtained to reference these results against. This does not disregard these results entirely, though, as general observations can be noted about the difference in the chemical shift of the nitrogen atom between Molecule 11 and Molecule 12.
The actual spectra themselves will not be shown as they are do not provide much insight into the nature of the molecule on their own (one singlet was observed on each spectra, as expected). Only the differences between values of chemical shift allow conclusions regarding the chemical environment of each nitrogen atom to be drawn.
The chemical standard chosen for this NMR was NH3.
| Molecule | Molecule 11 Chemical Shift /ppm | Molecule 12 Chemical Shift /ppm |
|---|---|---|
| d (iPr) | 135.2 | 123.7 |
| c (tBu) | 136.5 | 124.1 |
| b (Ph) | 136.2 | 124.1 |
This data clearly shows that the nitrogen atom is more deshielded in Molecule 11 than in Molecule 12. Furthermore, the chemical shifts predicted for each molecule are all within 1.3ppm of one another, with no apparent effect from altering the R- group. This makes 15N NMR ideal for distinguishing between the formation of Molecule 11 type products [oxygen connected to the azetidinone moiety], which should have a chemical shift in the range of (~135.8 ± 0.7)ppm and Molecule 12 type products [carbonyl connected to the azetidinone moeity], which should have a chemcial shift in the range of (~123.9 ± 0.2)ppm.
A particular reason for why this nitrogen atom is particularly more deshielded in Molecule 11-type products could not be determined. It was orginally considered that the N-H group formed part of a six membered ring (with hydrogen bonding between the ester carbonyl and the N-H group), however, the optimised geometry of the structure confirmed this was not the case, as the carbonyl group was not in the same plane as the N-H bond.
As mentioned before, the main disadvantage of this method is the low isotopic abundance of 15N nuclei (Natural abundance = 0.37%)[35].
Differentiating between the two regioisomers using IR Spectroscopy
The final method to differentiate between the two regioisomers 11 and 12 was through the use of Infrared spectroscopy. Unlike NMR, IR spectroscopy cannot give accurate data to distinguish between the chemical environments of different atoms. However, IR spectroscopy is by far the quickest and easiest of the three suggested techniques to be used. It was expected that the ester C=O Stretch would alter in stretching frequency, depending on its connectivity to other groups in the Product Molecules, thus providing a third method of determining the identity of an unknown regioisomer from the Baeyer-Villiger reaction.
The predicted IR spectra (Predicted by Gaussian, after optimisation) for all six product molecules are shown below, with the important characteristics tabulated below:
Predicted IR Spectrum for Molecule 11d - R- = i [36]Pr

Predicted IR Spectrum for Molecule 11c - R- = tBu [37]
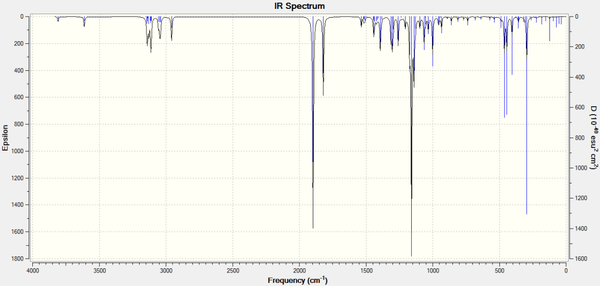
Predicted IR Spectrum for Molecule 11b - R- = Ph [38]
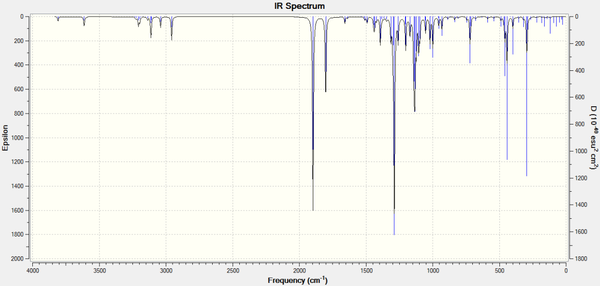
Predicted IR Spectrum for Molecule 12d - R- = iPr [39]

Predicted IR Spectrum for Molecule 12c - R- = tBu [40]

Predicted IR Spectrum for Molecule 12b - R- = Ph [41]

| Characterisation | 11d (R = iPr) | 12d (R = iPr) | 11c (R = tBu) | 12c (R = tBu) | 11b (R = Ph) | 12b (R = Ph) |
|---|---|---|---|---|---|---|
| C=O Stretch (in ring)/cm-1 | 1898.4 | 1892.8 | 1897.2 | 1892.3 | 1897.5 | 1892.2 |
| Ester C=O Stretch/cm-1 | 1845.3 | 1787.9 | 1820.2 | 1783.7 | 1802.3 | 1828.3 |
| (Non-carbonyl C)-O Stretch/cm-1 | 1075.7 | 1291.1 | 1064.6 | 1318.3 | 1020.5 | 1254.5 |
| N-H Bend/cm-1 | 455.4 | 446.4 | 444.2 | 444.5 | 443.1 | 442.8 |
From these results, several inferences can be made:
i) The N-H bend does not aid the determination of the type of regioisomer being characterised, indicating that is not caught up in a six membered ring for Molecule 12 (in which it hydrogen bonds to the carbonyl on the ester group).
ii) The C=O Stretch from the carbonyl in the azetidinone is not affected by regioisomerism, nor by R- group substitution.
iii) The (Non-carbonyl C)-O Stretch is the most indicative character in determining the regioisomer present. The bond between the azetidinone carbon and the ester oxygen in Molecule 11 produces a fairly reproducible frequency of stretching in the region of 1000-1100cm-1. When the ester oxygen is connected to the carbon of the R- group, as in Molecules 12b-d, on average a far higher frequency stretch is observed at ~1300cm-1.
What is by far the most interesting result, is that of the difference between the the ester carbonyl C=O stretches of Molecules 11b-d and 12b-d. For the R ≠ Ph product molecules, it is observed that the ester C=O group has a lower stretching frequency when directly attached to the azetidinone moiety. The origin of this difference in stretching frequency is not apparent. It is possible the proximity of the ester carbonyl group to the nitrogen atom in the four membered ring is directly related to this observation, this could provide the basis for a further experiment into the vibrational spectra of these sorts of compounds. The charge distribution on both of the oxygen atoms in the ester group, along with the carbonyl atom in the four membered ring for comparison, was determined on the Gaussian optimised structures of all six product molecules.
The results of this charge distribution determination is shown below:
| Molecule | Carbonyl within the ring | Ester Carbonyl | Ester Oxygen |
|---|---|---|---|
| 11d (iPr) | -0.474 | -0.445 | -0.481 |
| 12d (iPr) | -0.476 | -0.491 | -0.480 |
| 11c (tBu) | -0.479 | -0.474 | -0.499 |
| 12c (tBu) | -0.477 | -0.495 | -0.492 |
| 11b (Ph) | -0.479 | -0.481 | -0.508 |
| 12b (Ph) | -0.477 | -0.458 | -0.519 |
An image of a typical Mulliken charge distribution produced by the Gaussian software is shown below:
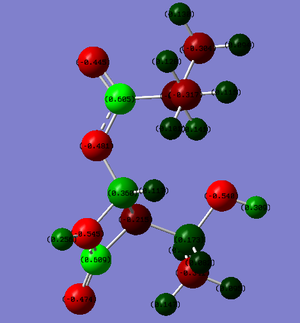
These results clearly show that the charge on the carbonyl oxygen situated within the ring (the carbonyl adjacent to the nitrogen atom, used for general comparison) does not fluctuate between any of the six products under consideration. Whereas, for the ester carbonyl group, there is a clear difference in charge distribution between Molecules 11 and 12. More negative charge seems to be situated on the carbonyl oxygen in Molecule 12 than in Molecule 11. This results in a greater charge disparity between the C atom and the O atom of the carbonyl group, which is indicative of a weaker bond between these two atoms. This situation is reversed for the R = Ph group (as with the IR spectral data), in which the ester carbonyl oxygen of Molecule 12 has less negative charge when compared to the ester carbonyl oxygen of Molecule 11. This information can be used to back up the predicted IR spectra. It is interesting to note that the charge distribution for the singly bonded oxygen on the ester group =(CO)-O-R or -O-(CO)-R does not alter significantly between Molecules 11 and 12. This is interesting, in that it suggests the the charge on the oxygen is almost entirely independent of whether it bonds to the azetidinone moiety or the R- group, for a particular R- group (i.e. the charge distribution on this oxygen changes with different R- groups, but not between different product molecules 11 and 12).
A possible further experiment has arisen as a result of these calculations. It would be interesting to run an IR spectrum on different molecules with the functionality shown in Figure 35(below).

The data from this experiment suggests that the Molecule 11-type species have a higher stretching frequency than the Molecule 12-type species, due to the increased strength of the carbonyl bond in 11-type species. It is possible that the presence of the Nitrogen atom in the ring has some form of bond strengthening effect. This can either be confirmed or disregarding by running an IR spectra on a series of these molecules, with variation in the R- group.
Overall, this mini-project has shown the effectiveness of Computatational methods in predicting the 13C NMR spectra for reasonably complex molecules. The results obtained from the NMR predicition agreed well with the literature values. Furthermore, through the prediction of specific IR vibrational modes, the basis for a new investigation into the stretching frequency of ester carbonyl atoms when situated in close proximity to a nitrogen atom has been set. Due to timing constraints, initial results for this further investigation could not be obtained.
References
- ↑ T. G. Lenz, J. D. Vaughn, J. Phys. Chem., 1989, 93, pp. 1592-1596, doi: 10.1021/j100341a081
- ↑ R. Woodward, R. Hoffmann, Agnew Chem., 1969, 8, pp. 781-853
- ↑ A. Turnbull, H. Hull, Aust. J. Chem., 1968, 21, pp. 1789-1797
- ↑ M. Saville et al., Lancet, 346, pp. 26-28
- ↑ W. Johnson et al., J. Am. Chem. Soc., 1961, 83, pp. 606-614, doi: 10.1021/ja01464a027
- ↑ T. A. Halgren, J. Comp. Chem., 1996, 17, pp. 491-519
- ↑ 3rd Year Computational Laboratory wiki, Module 1, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic
- ↑ J-S Kim, Bull. Korean Chem. Soc., 1997, 18, pp. 488-495
- ↑ 3rd Year Computational Laboratory wiki, Module 1, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic
- ↑ H. Rzepa et al., J. Chem. Soc. Perkin. Trans. 2., 1992, pp. 447-448
- ↑ http://hdl.handle.net/10042/to-10373
- ↑ http://hdl.handle.net/10042/to-10372
- ↑ E. Tate, 2nd Year Bio-Organic Chemistry Course, Lecture 5, 2011, p. 7
- ↑ Ü. Muller, Inorganic Strucutral Chemistry, Wiley, 1993, p.31
- ↑ S. Gibson, 1st Year Carbonyl Chemistry Course, Lecture 1, 2010 p. 4
- ↑ K. Faber, Biotransformations in Organic Chemistry, Springer, 2011, pp.192-197
- ↑ M. Laurent, et al., J. Org. Chem., 2004, 69, pp.3194-3197
- ↑ A. Spivey, 3rd Year Stereoelectronics Course, Lecture 5, 2011 p. 6
- ↑ M. Laurent, et al., J. Org. Chem., 2004, 69, pp.3194-3197
- ↑ http://hdl.handle.net/10042/to-10450
- ↑ http://hdl.handle.net/10042/to-10451
- ↑ http://hdl.handle.net/10042/to-10448
- ↑ http://hdl.handle.net/10042/to-10449
- ↑ http://hdl.handle.net/10042/to-10446
- ↑ http://hdl.handle.net/10042/to-10447
- ↑ D. Braddock, H. Rzepa, J. Nat. Prod., 2008, 71, pp. 728-730
- ↑ 3rd Year Computational Laboratory wiki, Module 1, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic
- ↑ http://hdl.handle.net/10042/to-10452
- ↑ 3rd Year Computational Laboratory wiki, Module 1, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic
- ↑ http://hdl.handle.net/10042/to-10453
- ↑ http://hdl.handle.net/10042/to-10459
- ↑ http://hdl.handle.net/10042/to-10454
- ↑ http://hdl.handle.net/10042/to-10463
- ↑ http://hdl.handle.net/10042/to-10455
- ↑ P. Lickiss, 2nd Year NMR and EPR Spectroscopy Course, NMR data tables, 2010, p.1
- ↑ http://hdl.handle.net/10042/to-10466
- ↑ http://hdl.handle.net/10042/to-10468
- ↑ http://hdl.handle.net/10042/to-10470
- ↑ http://hdl.handle.net/10042/to-10467
- ↑ http://hdl.handle.net/10042/to-10469
- ↑ http://hdl.handle.net/10042/to-10471