Rep:Mod:ms mod3
Module 3: Transition state and reactivity
The Cope Rearrangement
Sigmatropic rearrangements are a class of pericyclic reactions controlled by orbital symmetry. During the rearrangement one σ bond is made while another is broken in a concerted mechanism. It also involves migration of an atom or group from one point in a conjugated system to another. Sigmatropic rearrangements are classified by a double numbering system that refers to the relative position of the atom or group involved in the migration. [1]
An example of a [3,3] sigmatropic rearrangement is The Cope rearrangement shown below.
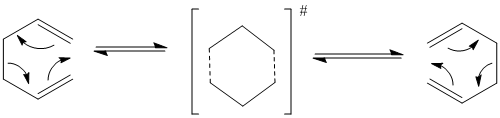
This rearrangement passes through a transition state that can either exist as the chair or boat form.

In this section, the transition state through which this reaction goes through will be investigated. However, initially the reactant/product will be analysed to find the minimum energy confirmation.
Optimising the Reactants and Products
To find the lowest conformation of 1,5 hexadiene different conformations are investigated. There are 2 possible conformations; the gauche and anti, when looking down the bond between carbon 3 and carbon 4. This is shown below.
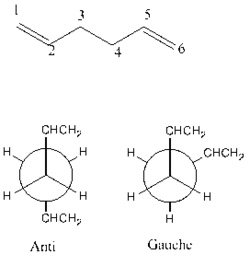
Depending on the positions of the -CHCH2 group there are a number of different conformations within anti and gauche. The structures were optimised in Gaussview using the Hartree-Fock method and a basis set of 3-21G. The method determines apporoximations used when solving the Schrodinger equation, and the basis sets determines orbitals used to approximate real orbitals.
Below are the results for the optimisations.
| 1,5 hexadiene conformation | Picture/Jmol | Energy (Hartrees) | Point group | Link to file |
| anti1 |  |
-231.69260 | C2 | DOI:10042/to-10036 |
| gauche4 |  |
-231.69153 | C2 | DOI:10042/to-10037 |
| gauche3 | 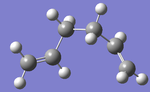 |
-231.69266 | C1 | DOI:10042/to-10038 |
| anti2 | 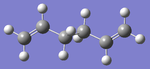 |
-231.69254 | Ci | DOI:10042/to-10040 |
The structures were compared to Appendix 1 and named accordingly.
It can be seen that the lowest energy conformation of 1,5 hexadiene is a gauche conformation (Gauche3). This is an unexpected result as in gauche conformation there are steric interactions between the 2 larger groups next to each other resulting in a higher energy. This steric clash is not present in the anti conformation since the groups are opposite each other.
This can be explained due to electronic interactions. In the gauche conformation the 2 pi orbitals are in an orientation such that they overlap. This interaction decreases the energy more than steric clash increases it making gauche3 most stable. This overlap is not present in the anti conformations. This is because the alkenes are orientated in such a way that they are too far away for any pi interaction to take place. An NBO analysis would help analyse molecular orbitals and confirm this explanation.
Optimisation of Ci with HF and DFT methods
The anti2 conformation of 1,5 Hexadiene with Ci symmetry was optimised with HF/3-21G (above). It was reoptimised with B3LYP/6-31G(d). The summary of the optimisation is shown below. DOI:10042/to-10173
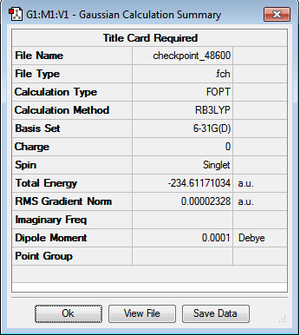
The DFT method results in a much lower energy conformation i.e by 3 a.u. This is because it uses a higher level of theory. However energies are not directly comparable using different methods and basis sets. Therefore further parameters need to be investigated and compared. Below is a table summarising these.
| Structural parameter | HF/3-21G | B3LYP/6-31G(d) | Literature[2] |
| C=C bond length | 1.316 | 1.333 | 1.326 |
| -C-C bond length | 1.553 | 1.548 | 1.524 |
| =C-C bond length | 1.509 | 1.504 | - |
| C-H bond length | 1.086 | 1.098 | 1.099 |
Both methods give structural data that is very similar to that seen experimentally. However the B3LYP/6-31G(d) gives a slightly better approximation when compared to the literature values. This is because it is a more complex method than the Hartree-Fock/3-21G method.
Frequency calculation
Frequency calculations can also be performed to get data comparable to what is seen experimentally. This includes the sum of electronic and zero point energies (Electronic energies and vibrational energies at 0K), sum of electronic and thermal energies (electronic and vibrational energies at 298K), Sum of electronic and thermal Enthalpies (sum of electronic and thermal energies with enthalpy correction) and sum of electronic and free energies (sum of electronic and thermal energies with entropy correction). Below is a summary of these quantities carried out with B3LYP/6-31G(d) method. Media:ms_anti2_freq.out
| Contribution | Energy (Hartree) |
| Sum of electronic and zero-point Energies | -234.469212 |
| Sum of electronic and thermal Energies | -234.461856 |
| Sum of electronic and thermal Enthalpies | -234.460912 |
| Sum of electronic and thermal Free Energies | -234.500821 |
These values can be used to give predictions of energy changes for a reaction and can be compared with experiments
Optimisation of 'chair' and 'boat' transition structures
The Cope Rearrangement can either go through a 'Chair' transition state ot a 'boat' transition state. In order to find out which of the two possible transition states the Cope rearrangement proceeds by the energies of the two transition states have to be found and compared. There are a number of methods by which transition states are optimised, some of which are used below.
Chair
There were 2 possible methods used for optimising the chair transition state.
Method 1: DOI:10042/to-10174 The structure is built approximately like the predicted transition state, and then it is optimised (as a transition state) The force constants are calculated once, knowing that a transition state has one imaginary frequency. For the chair transition state the allyl fragment was drawn and optimised using the HF/3-21G method and basis set. This optimised structure was copied into new window, and a second molecule appended into the same. Fragments were arranged so as the distnace between the terminal carbons of the allyl fragments were approximately 2.2A. A gaussian optimisation for a transition state was set up, selecting Opt+Freq as the job type and Optimisation as TS (Berny). The HF/3-21G method and basis set were used and additional keywords of Opt=NoEigen were put in, which stops calculations from failing if a second negative frequency is calculated for a particular conformation.
The optimised structure gave a frequency calculation of -818 cm-1. This vibration is shown below and clearly corresponds to the concerted fashion in which one sigma bond is breaking and one sigma bond forming.
Method 2: DOI:10042/to-10175 The other method used was the 'freeze coordinate' method. The approximate structure of the transition state was used for the optimisation however instead of calculating force constants to optimise the chair tranisition state to the lowest energy conformation the distance between the 2 pairs of terminal carbons were frozen. The structure was then optimised using the Hartree-Fock method and a basis set of 3-21G. Apart from the bond forming and that breaking the resulting structure is fully optimised. By performing an optimisation of this structure using TS(Berny) the 2 bond lengths were calculated and normal guess Hessian was used to gain information about the positions of the terminal carbons.
The resulting imaginary frequency calculated using this method is also -818cm-1. This corresponds to the bond forming and breaking in the transition state.
Below are images comparing bond lengths for the 2 methods.
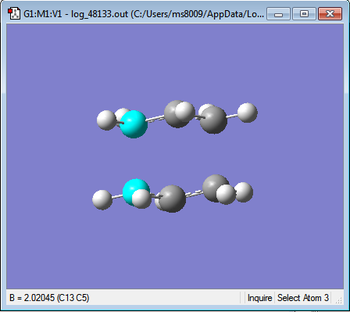 |
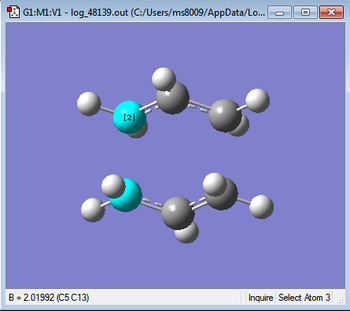 |
As can be seen the bond lengths are the same to 2 d.p and hence are valid
| Force Constant Method | Freeze Coordinate Method | |
| Energy (Hartrees) | -231.6193 | -231.6193 |
| Gradient on the Energy Surface (Hartrees) | 0.00001603 | 0.00005412 |
| Sum of Electronic and Zero Point Energies (0K) | -231.4667 | -231.4667 |
| Sum of Electronic and Thermal Energies (298K) | -231.4613 | -231.4613 |
From the gradient it can be seen that a minimum was in fact reached. It can also be seen that the data obtained from both methods is exactly the same and so it can be said that both methods are valid and reproduce reasonable results.
Boat
The boat transition state was found by using the QST2 method. In this method the reactant and product are given and the calculation finds the transition point between the two molecules. To ensure a successful computation, the reactants and products must be numbered in the same way. Hence these numbers were manually changed to correspond to each otnher. Below are the reactant and product for the Cope rearrangement based on the anti2 conformation of 1,5 Hexadiene.
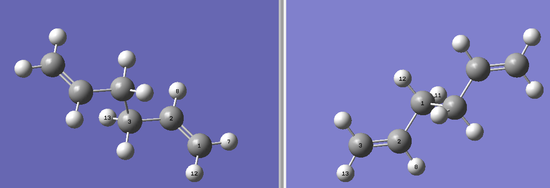
A QST2 transition state opt+freq calculation was then run, using HF/3-21G. The resulting transition state is shown below. DOI:10042/to-10172
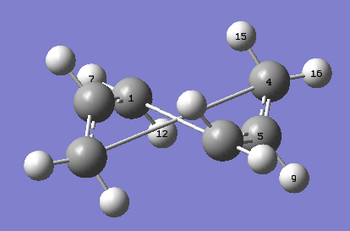
It can be seen that the optimisation failed, and instead of the boat transition state a more dissociated chair like transition state was obtained. This is because when the calculation interpolated between the 2 structures, it simply translated the top allyl fragment and did not consider the possibility of rotation around the central bonds. Hence the QST2 method cannot locate the transition structure for this rearrangement.
QST2 optimisation calculation was carried out again but the reactant and product conformation were changed by changing the central C-C-C-C (C2-C3-C4-C5) dihedral angle to 0o and the side C-C-C (C2-C3-C4 and C3-C4-C5) angle to 100o. Once again it was ensured that the atom numbers corresponded exactly to each other.

On optimisation the calculation failed. This calculation was repeated several times and atom numbers checked over but the calculation was just not successful. Looking at the log file it was seen that the structure just did not optimise. Hence several things were tried e.g using higher level of theory (B3LYP/6-31G(d) and increasing the number of cycles. These did not help. The demenstrator finally suggested using the DFT optimised anti2 conformation as the reactant and produce, and this calculation was finally successful. DOI:10042/to-10176 The geometry converged and only one imaginary frequency of -840cm-1 was obtained and is shown below. The final boat transition structure obtained is also shown below.
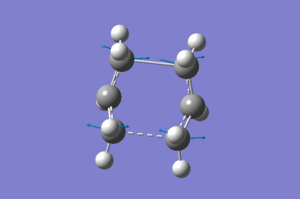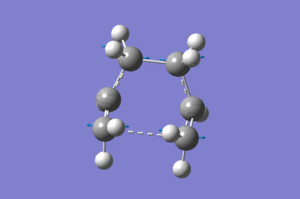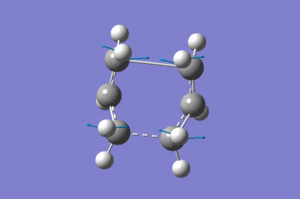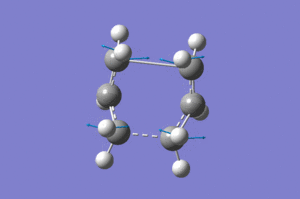 |
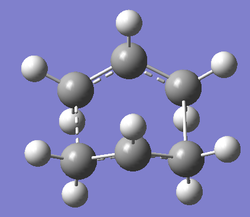 |
The vibration mode corresponds to the concerted formation and cleavage of sigma bond involved in the cope rearrangement. Although QST2 method has some advantages, it can often fail if the reactants and products are not close to the transition structure.
Below is a table of energies and bond lenghths obtained from the QST2 method.
| QST2 | |
| Energy (Hartrees) | -231.6028 |
| Gradient on the Energy Surface (Hartrees) | 0.00016358 |
| Sum of Electronic and Zero Point Energies (0K) | -231.4509 |
| Sum of Electronic and Thermal Energies (298K) | -231.4453 |
| C-C bond length for sigma bond forming/breaking (A) | 2.14 |
From the gradient it can be seen that a minimum was in fact reached.
If the energies of the boat transition state is compared to that of the chair TS it can be seen that the chair TS is more stable.
IRC calculations
Although the two transition states have been found it is unknown which of the conformations of 1,5 Hexadiene is required for a cope rearrangement to occur to reach one of these 2 transition states. As mentioned it is predicted that anti2 is the conformation that does this. This needs to be proved.
An Intrinsic Reaction Coordinate (IRC) calculation is carried out for both transition states. The IRC was only calculated in one direction since the reaction was symmetrical (the reactants and products are the same). The results of these calculations are shown below.
Chair
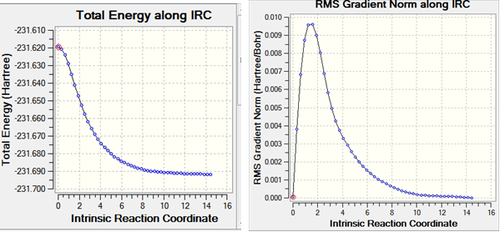
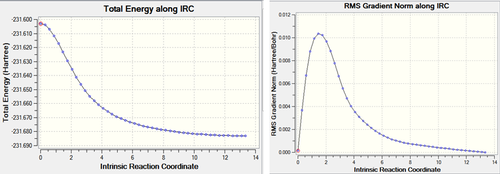
After the IRC calculation, the resulting file had 21 intermediate geometries. Below is the resulting graph and animation showing the 21 intermediates.Media:ms_chair_IRC.log
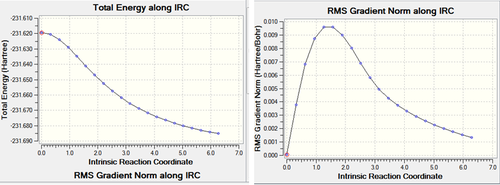
As can be seen from the graphs above the calculation has not completed to give a minimum energy comformation. This is suggested by the fact that on the IRC graph does not reach a minimum (energy) point and the grandient on the IRC does not reach zero (and the gradient at a minimum (energy) point is always zero).
Therefore, two methods were tried in order to try to find the minimum energy conformations.
Method 1: The last comformation of 1,5 Hexadiene given on the IRC was optimised to its lowest energy comformation using the Hartree-Fock calculation method and the 3-21G basic set. Below are the graphs, images and jmols comparing the initial and minimised structures. Media:chair_IRC_method1.log
 |
 |
Method 2: The second method employed was running the IRC calculation again and calculating the force constants at every step (not just once) in order to find the lowest energy conformation for the chair TS. Below are the graphs and images.Media:chair_IRC_method2.log
As can be seen from above both these method gave very similar structures. From the graphs it can be seen the structures did infact minimise.
Note: Another possible method to reach minimisation is specifying a larger number of points until a minimum is reached. This was not carried out because initially the number of points was edited to 50, and if only 21 structures were computed then 50 is more than enough.
| Parameter | IRC | Method 1 | Method 2 | |
| Energy (Hartrees) | -231.68514 | -231.69167 | -231.69167 | |
| Gradient (Hartrees) | 0.00133735 | 0.00000596 | 0.00001172 | |
| Bond length (A) | C=C | 1.32 | 1.33 | 1.32 |
| C-C | 1.51 | 1.51 | 1.51 | |
| C-C breaking | 3.07 | 4.51 | 4.36 | |
| C-C forming | 1.57 | 1.54 | 1.55 | |
| C-H | 1.08 | 1.1 | 1.09 |
As can be seen from the gradient, the initial IRC did not reach a minimum. This results in different bond lengths from the other 2 methods employed. From the energy above it can be seen the the chair TS corresponds to the gauche2 conformer (cf appendix 2).
Boat
IRC calculation carried out on boat optimised transition structure yielded 26 intermediate geometries. Below are the graphs and the animation showing the transition from each geometry calculated.Media:ms_boat_IRC.log
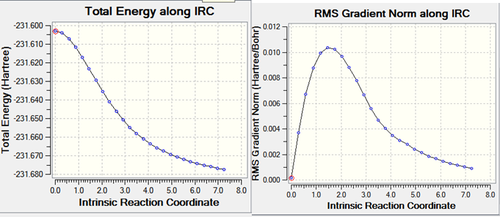 |
 |
 |
As can be seen from the graphs above the calculation has not completed to give a minimum energy comformation. This is suggested by the fact that on the IRC graph does not reach a minimum (energy) point and the grandient on the IRC does not reach zero (and the gradient at a minimum (energy) point is always zero).
The methods described above for the Chair TS were carried out to ensure minimisation occurs.
Results from method 1: Media:ms_boat_IRC_method1.log
Results from method 2: Media:ms_boat_IRC_method2.log
47 intermediate geometries were calculated
From the graphs it can be seen the structures did minimise. It can also be seen that the structures obtained by both methods are very similar.
| Parameter | IRC | Method 1 | Method 2 | |
| Energy (Hartrees) | -231.6772638 | -231.6830255 | -231.6830253 | |
| Gradient (Hartrees) | 0.00091436 | 0.00001764 | 0.00000563 | |
| Bond length (A) | C=C | 1.32 | 1.32 | 1.32 |
| C-C | 1.51 | 1.51 | 1.51 | |
| C-C breaking | 1.59 | 1.58 | 1.58 | |
| C-C forming | 3.32 | 4.35 | 4.34 | |
| C-H | 1.08 | 1.09 | 1.08 |
As can be seen from the gradient, the initial IRC did not reach a minimum. This results in different bond lengths from the other 2 methods employed. However the energy obtained from method 1 or method 2 does not correspond to a conformer in appendix 2.
Activation energies
As well as identifying the transition states, the vibrational analyses carried out above can give useful information about the energies of the transition states, as was seen for the reactants in the first part. To gain this information in an accurate way, the final structures of the transition states gained at the HFT/3-21G level of theory were re-optimised and the vibrational analysis carried out at the higher B3LYP/6-31G* level of theory.
The tables below compare the thermochemistry data obtained from the two methods for the boat transition state and the chair transition state.
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.6193 | -231.4667 | -231.4613 | -234.5570 | -234.4149 | -234.4090 |
| Boat TS | -231.6028 | -231.4509 | -231.4453 | -234.5431 | -234.4023 | -234.3960 |
| Reactant (anti2) | -231.6926 | -231.5395 | -231.5325 | -234.6117 | -234.4692 | -234.4619 |
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.68 | 44.68 | 34.07 | 33.20 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.71 | 41.98 | 41.35 | 44.7 ± 2.0 |
Note: 1 Hartree = 627.509 kcal/mol. HF reference to the the Hartree-Fock calculation method. Energy difference found between Reactant(anti2) and Sum of Electronic and Zero-point Energies for 0K, and Reactant (anti2) the Sum Electronic and Thermal Energies for 298K
It can be seen that the energy difference is less between the reactant and the Chair TS compared to the reactant and the Boat TS, suggesting that the Cope rearragement goes though a Chair Transition state. It can also be seen that the calculations and the resulting energy difference for the more complex B3LYP 6-31G d calculation/basic set combination are closer to what is seen experimentally[3] compared to the Hartree-Fock 3-21G calculation/basic set combination.
The Diels Alder Cycloaddition
The reaction between cis-butadiene and ethene
The prototypical Diels Alder cycloaddition is between ethylene and butadiene, with butadiene as the diene and ethylene as the dieneophile.
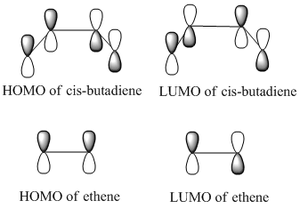
Since butadiene is in the cis conformation it belongs to the C2v point group, and ethylene belongs to the D2h point group. Therefore both are symmetric about a σv plane of symmetry. The frontier orbitals of these reactants will be symmetric (s) or antisymmetric (a). These orbitals can be predicted qualitatively by the linear combination of atomic orbitals (LCAO) method. In this case, the frontier orbitals will be created by combining p-orbitals to create MOs with either π or π* symmetry. As can be seen, the predicted HOMO of cis-butadiene is antisymmetric with respect to this plane of symmetry, whilst its LUMO is symmetric. On the other hand, the HOMO of ethylene is symmetric whilst its LUMO is antisymmetric. This suggests that either the HOMO of cis-butadiene interacts with the LUMO of ethylene, or the HOMO of ethylene with the LUMO of cis-butadiene.
 |
 |
The molecular orbitals of the reactants were found by first optimising the structures and then calculating the energy. Both were done using the semi empirical AM1 method. The resulting orbitals are shown below.
 |
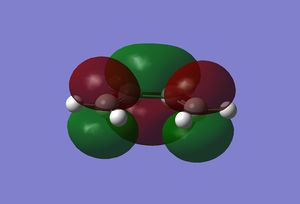 |
 |
 |
As can be seen, the symmetry of the frontier orbitals predicted was in fact correct. Furthermore, it can be seen that the HOMO and LUMO of butadiene are formed by the combination of the π and π* orbitals of ethylene, and that the qualitative LCAO method used above is actually quite accurate in predicting the shape of the resultant MOs in this case. However, to test which HOMO interacts with which LUMO, the transition state of the cycloaddition must be computed, as was done for the cope rearrangement above.
This was done by guessing a structure for the transition state based upon an envelope geometry. This was optimised using the redundant coordinate editor as before to freeze the reaction coordinate. An optimisation and frequency analysis was then carried out on this optimised structure to gain the optimised transition state, and ensure that it is in fact the transition state.
The transition state was indeed found, as indicated by the presence of an imaginary frequency at -938cm-1 in the vibrational analysis.Media:ms_cisbutadiene_frozencoord_AM1.log
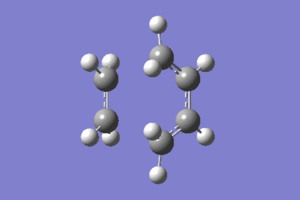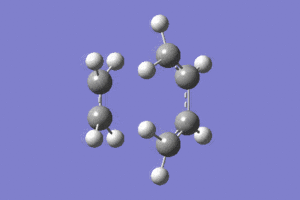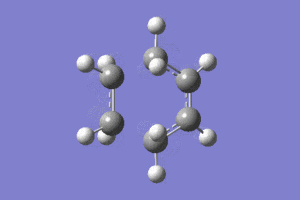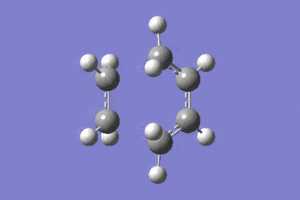 |
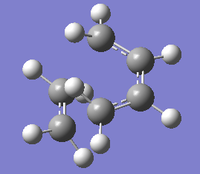 |
The imaginary frequency shown above confirms that this is the transition state for the cycloaddition, as the movement indicates the formation of a bond between the terminal cis-butadiene carbons and the ethylene carbons. These also indicate that the formation of these two bonds is synchronous, supporting the observation that the Diels Alder cycloaddition occurs in a concerted fashion.
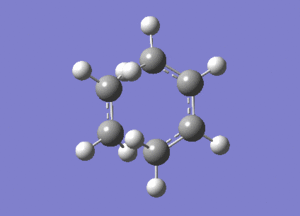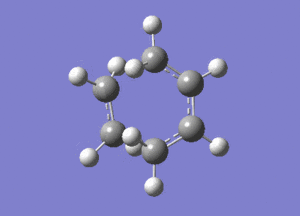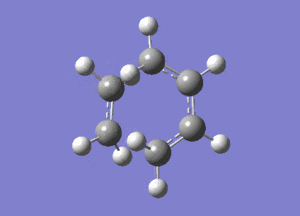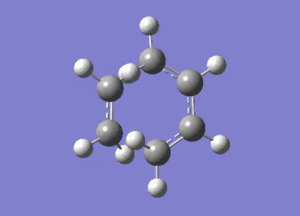
The lowest positive frequency for the transition state at 147cm-1 is shown above.This does not correspond to any bond forming or breaking.
It can seen when comparing the two vibrations, the bond forming vibration is symmetric (hence why the bonds form synchronous) compared to the lowest positive frequency vibration which corresponds to the wagging of the ethylene molecule in relation to the cis-butadiene molecule, and is antisymmetric.Media:ms_cisbutadiene_ethene_MO.log
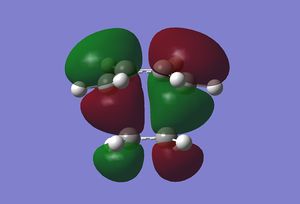 |
 |
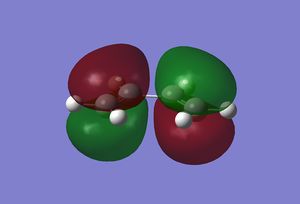
The HOMO of the transition state shows the formation of two σ-bonds by the overlap of the antisymmetric HOMO orbital of cis-butadiene with the antisymmetric LUMO of ethylene. The LUMO however can be seen to be the overlap of the symmetric HOMO of ethylene with the symmetric LUMO of cis-butadiene. Overall both the molecular orbitals are antisymmetric with respect the plane described above. The overlap of these orbitals is allowed as they have the same symmetry with respect to the mirror plane described above.
The two partly formed C-C σ-bonds are both 2.12 A long. The C-C(ethylene) bond length is 1.38 A, as is the length of the two terminal C-C bonds in the cis-butadiene molecule. The middle C-C bond in the cis-butadiene molecule is 1.40 A. The literature values found were 1.34 A[4] for the average sp2 C-C bond, and 1.54 A[5] for the average sp3 C-C bond. Thus, the two partly formed σ-bonds are significantly longer than a normal sp3 C-C bond but shorter than twice the carbon atom Van Der Waals radius(1.7A), showing that it is in fact a transition state. Furthermore, all of the other C-C bonds are somewhere in between the two literature values, showing that the π-bonding of the reactants is being disrupted and the hybridisation of the carbons is changing.
The reaction between Cyclohexa-1,3-diene and Maleic Anhydride
For the reaction between cyclohexa-1,3-diene and Maleic Anhydride there are 2 possible products as shown below.
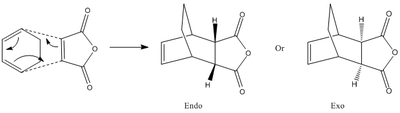
When the reactants are both cyclic, regiostereochemical implications develop. In such cycloadditions, either the exo or endo product can be formed. In some cases a preference for the exo product has been observed, which has been explained by the formation of secondary orbital interactions.[6]
The overlap of orbitals that are not involved in the formation of the 2 new sigma bonds result in secondary orbital interactions. As can be seen, this is only possible when the reactants approach each other to form the endo-product rather than the exo.
Thus, where SOIs occur, the endo-transition state is stabilised, thus lowering the kinetic barrier to the formation of the endo-product.
In this section this reaction will be investigated using the semi empirical AM1 method. The structure was optimised to TS Berny using the 'Frozen Coordinate' method and calculating the force constants once. However this calculation did not work, and failed every time. The force constants were then calculated at every point (always) and the calculation succeeded.
Below are the results for the Exo TS and Endo TS.
Exo Transition State
As normal, the transitions state was checked to be in the correct comformation by checking it had one negative frequency and that it had a motion relating to the bonds forming in the reaction. This was seen at -812cm-1 for the exo tranisition state as shown below Media:ms_DA_exo_froxencoord.log
 |
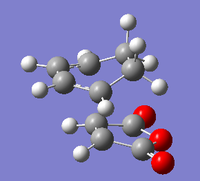 |
Below are the molecular orbitals obtained from the calculations. Media:ms_DA_exo_MO.log
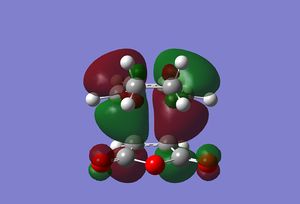 |
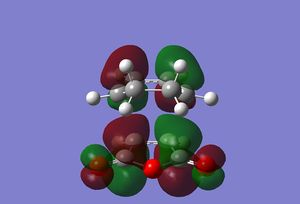 |
Endo Transition State
An imaginary frequency at -806 cm-1 was obtained confirming that a transition state was calculated. The motion of this imaginary frequency is shown below, representing the bonds forming in the reaction.Media:ms_DA_endo_frozencoord.log
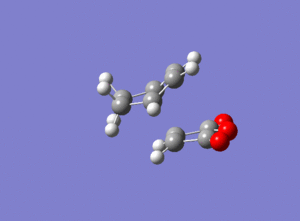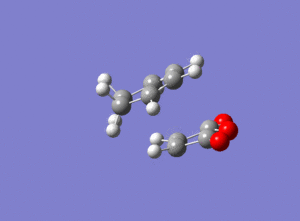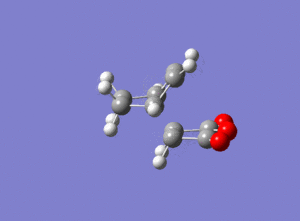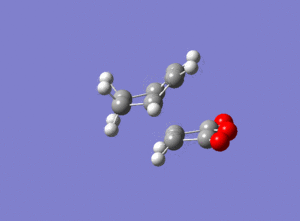 |
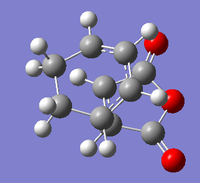 |
The structure obtained from the optimisation above was sent for an MO calculation. Below are the results. Media:ms_DA_endo_MO.log
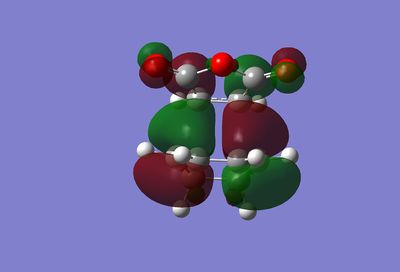 |
 |
As a result of being formed from the antisymmetric orbitals of the reactants, all the above orbitals are antisymmetric with respect to the mirror plane described before. In the HOMOs of both transition states, the partially formed σ-bonds can be seen. If any secondary orbital interaction was present in these molecular orbitals, a region of delocalised electron density would be expected between the carbonyl carbon and the cyclohexa-1,3-diene π-orbitals on each side of the transition state. However, as can be seen, in the HOMO of each this delocalisation is not present at all.
This suggests that there is no stabilisation due to secondary orbital interactions. Although this may well be the case, it could also be a result of the low-level of theory used. Furthermore, the size of the interactions may be too small to visualise.
| Exo | Endo | ||||
| Parameters | Freeze Coordination method | Final TS | Freeze Coordination method | Final TS | |
| Total Energy (Hartrees) | -0.05433 | -0.05042 | -0.05468 | -0.0515 | |
| RMS gradient (Hartrees) | 0.00682854 | 0.00000008 | 0.00637018 | 0.00000007 | |
| Bond lengths (A) | C=C | 1.42 | 1.42 | 1.42 | 1.39 |
| C-C | 1.52 | 1.52 | 1.52 | 1.52 | |
| C-H | 1.13 | 1.13 | 1.13 | 1.13 | |
| C=O | 1.22 | 1.22 | 1.22 | 1.22 | |
| C-O | 1.41 | 1.41 | 1.41 | 1.41 | |
| C-C forming | 2.1 | 2.17 | 2.1 | 2.16 |
As can be seen the bond lengths are very similar and hence it can be concluded that the mechanism for this reaction is a concerted one and can therefore be classified as a synchronous bond formation. The endo is more stable since it has a lower overall energy.
Conclusion
The use of computational methods can be justified to predict the transition states and corresponding activation energies. The results are in good agreement with experimental values. This is especially true for the B3LYP/6-31G(d) method of optimisation. Using this higher level of theory compared to the HF/3-21G shows a clear improvement in accuracy for energies and bond lengths.
References
- ↑ J. Singh in Photochemistry And Pericyclic Reactions,New Age International,2nd edn.,2005,97-98
- ↑ Handbook of Chemistry & Physics 2011-2012, 92nd Edition, 9-6
- ↑ Wiest, O.; Black, K.A.; Houk, K.N., J. Am. Chem. Soc., 1994, 116, 10336-10337DOI:10.1021/ja00101a078
- ↑ Stoicheff, B.P., Tetrahedron, 1962, 17, 135-145DOI:10.1016/S0040-4020(01)99013-1
- ↑ Bartell, L.S., J. Am. Chem. Soc., 1959, 81 (14), 3497-3498 DOI:10.1021/ja01523a002
- ↑ Clayden, Greeves, Warren, Wothers, Organic Chemistry, 2001, Oxford University Press, Oxford, pp916-7