Rep:Mod:ms mod2
Module 2: Bonding (Ab initio and density functional molecular orbital)
Introduction
For this module, to acquire an understanding of the structure and bonding of inorganic complexes quantum mechanical calculations are carried out. The Ab Initio ("from first principles") technique calculates molecules based on solutions of Schroedinger's equation and the wavefunction used. No empirical data is used. Throughout this lab DFT calculations with the B3LYP method is used. The B3LYP establishes the type of approximations that are made in solving the Schroedinger equation.
BH3
Geometry Optimisation
During this process a rough geometric approximation is made and then computationally made as exact as possible. A series of iterations are carried out on the molecule until the energy of the molecule has reached a minimum. BH3 was optimised using DFT calculations with B3lYP functional and 3-21G as the basis set. Although this basis set has a low accuracy the calculations are carried out very quickly making it an ideal basis set.
Basis set: Group of constants used in wavefunctions. Named by number and type of wavefunctions used to represent an atom, and is specific to an atom.[1]
Below is the image and Jmol of the optimised structure.
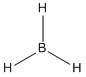
The summary of calculations are shown below.
All bond angles: 120
All bond lengths: 1.19A
| BH3 optimisation | ||
| File Name | bh3_opt | |
| File Type | .log | |
| Calculation Type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -26.462 +/- 3.808x10-3 | a.u. |
| RMS Gradient Norm | 0.000 +/- 3.808x10-3 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 0.00 +/- 0.005 | Debye |
| Point Group | D3H | |
| Job Time | 26.0 | Seconds |
The resulting log file was checked to ensure the optimisation had converged. This is shown below. As can be seen all parameters had converged and hence it is definite that the job has completed successfully.
Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES Predicted change in Energy=-1.071764D-06 Optimization completed. -- Stationary point found.
The optimisation went through 4 iterations. Below are the corresponding images.
For us to understand the optimisation procedure it is important to look at the Born Oppenheimer approximation. This approximation states that electrons move alot faster than the relatively slow nuclei. Although the wavefunction of the electrons still depends on the positions of the nuclei (due to Coulomic attraction, it does no depend on the momenta of nuclei.
During optimisation, by solving the Schrodinger equation under the Born Oppenheimer approximation the energy of the system is calculated. This is done for a given set of nuclear positions.
Nuclear positions are represented by R, hence the energy calculated by solving the Schrodinger equation at these positions is E(R). Forces of the interactions between electrons and nuclei are calculated at R. Then, the nuclear positions are altered (R changed to R’). Energy E(R’) and forces at R’ are calculated too. The rate of change E(R) with R is calculated for every iteration. This is the Root Mean Squared Gradient.
The structure of the lowest energy is the ‘optimised’ structure; a minima on the potential energy surface. The procedure of reaching the minima from a starting point is ‘optimisation’. The root mean squared gradient at the optimised structure is 0 since minima is a stationary point. The procedure of energy calculation, gradient calculation and nuclear position adjustment is repeated iteratively until a stationary point is reached.
The figures below show the optimisation for BH3.
Although a stationary point has been found, it is not definite that the job converged to a minimum and the right minimum if it actually has. Vibrational analysis is needed to confirm this.
At a minima, movemement of atoms (and hence electrons) relative to others would result in a higher energy state, energy would have to be put in for this to happen. At a maxima however, any change would result in a decrease in E(R) and therefore energy would be released.
This helps differentiate between convergence to maxima or minima. Maxima will have one negative vibrational frequency and hence a stationary point would not have been found. Minima will have entirely positive vibrational frequencies.
Vibrational Analysis
DFT-B3LYP was used with 3-21G as the basis set for calculating vibrational frequencies of the optimised structure of BH3.
The same calculation type and basis set is necessary as the optimised structure in only a minima calculated using these specific directives. It wouldn’t necessarily be a minima on the Potential Energy Surface calculated by other methods. Hence it is importnant to note that calculations are accurate only to the level of theory and basis set used.
The summary for the frequency calculation is shown below.
| BH3 frequency | ||
| File Type | .chk | |
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| Total Energy | -26.462+/- 3.808x10-3 | a.u. |
| RMS Gradient Norm | 0.000+/- 3.808x10-3 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 0.00 +/- 0.005 | Debye |
| Point Group | D3H |
As can be seen the total energy was found to be the same as that recorded for the optimisation. Hence it confirms that the optimisation converged at a minima.
The results of the frequency analysis is shown below.
| Stretching mode number | Form of vibration | Description | Image | Frequency/cm-1 | Intensity | Symmetry D3h point group |
| 1 | Out of plane wagging | Boron moves in the opposite direction from the 3 hydrogens at all times. The 3 hydrogens move together in the z direction. Centre of mass does not change. |  |
1144.2 | 93 | A2'' |
| 2 | Scissoring (bending motion) | The two hydrogens moving down are offset by boron and the remaining hydrogen moving upwards. 2 H-B-H angles are stretched while one H-B-H is constricted. Centre of mass does not change. |  |
1203.6 | 12 | E' |
| 3 | Rocking (bending motion) | One H-B-H angle is constricted, the other expanded and the third held constant. A large movement of hydrogen changes 2 H-B-H angles and is offset by smaller movements of the rest of the atoms so as to preserve centre of mass. |  |
1203.6 | 12 | E' |
| 4 | Symmetric stretching | B-H bonds symmetrical stretch at the same time. Boron does not move throughout the vibration. Symmetrical vibration ensures Centre of Mass is preserved. |  |
2598.4 | 0 | A1' |
| 5 | Asymmetric stretching | Two B-H bonds lengthen and shorten asymmetrical. One B-H bond stays constant. |  |
2737.4 | 104 | E' |
| 6 | Asymmetric stretching | 2 B-H bonds stretch symmetrically whereas the third stretches asymmetrically. 2 B-H bonds lengthen while the third shortens, boron will move upwards so there is no change in the centre of mass over the vibration. |  |
2737.4 | 104 | E' |
It can be seen that no negative stretching frequencies were calculated showing that the optimised structure is at an energy minimum. A comparison to experimental data is made to be certain that the structure is correctly optimised. This is done by comparing bond lengths and bond angles.
The H-B-H angles were all measured as 1200+/- 0.050. The B-H bond lengths were all measured at 1.19A +/- 0.005 which is in exact agreement with the literature value of 1.19A.[2] This confirms that the structure is optimised successfully.
Below is the calculated IR spectrum.
We have calculated 6 vibrations however in the IR spectrum there are only 3 peaks observed.
For an absorption to occur there must be a non-zero transition dipole moment. And in order to see a peak in an IR the light absorbed must be in the IR frequency range.
From the table above it can be seen that for Stretching mode number 4 there is no change in dipole moment. The stretching is totally symmetric and therefore the band would be IR inactive.
It can also be seen that the Stretching mode numbers 2 and 3 are degenerate-since they both have the E’ label. They are of the same energy and therefore occur at the same frequency. Stretching modes 5 and 6 are also degenerate, occurring at 2737.4 cm-1.
Thus 3 peaks are observed; 1 vibration is totally symmetric and therefore not seen, 2 vibrations correspond to IR active degenerate pairs if vibrations and the IR active vibration at 1203.6 cm-1.
Molecular Orbitals
Population analysis was carried out with the DFT-B3LYP method and a basis set of 3-21G as well as full NBO. The molecular orbitals from this analysis are seen below. From this it can be seen that the 3a' MO is higher in energy than the 2e' MO. This can change with a change in basis set and calculation type used.
As can be seen the calculated molecular orbitals match up very closely with the qualitative LCAO molecular orbitals.
Although qualitative molecular orbital theory is a quick way of understanding the reactivity of compounds and even though it is accurate and quick, computational molecular orbital theory is more useful for complex systems.
NBO analysis
NBO analysis takes a delocalised MO picture and returns a 2 electron-2 centre picture of bonding.
A summary of Natural Population Analysis was found in the log file. This shows charges and the population of core orbitals. The summary is shown below:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.27845 1.99954 2.72201 0.00000 4.72155
H 2 -0.09282 0.00000 1.09266 0.00015 1.09282
H 3 -0.09282 0.00000 1.09266 0.00015 1.09282
H 4 -0.09282 0.00000 1.09266 0.00015 1.09282
=======================================================================
* Total * 0.00000 1.99954 6.00000 0.00046 8.00000
Below is a image representing the natural charges of the molecule. The red denotes negative charge, and green positive.
Based on the Lewis structure of the compound boron is expected to be electron deficient. This can be seen on the image, as expected.
On further examination of the log file the bonding in the compound can be determined. This is in terms of hybridisation. This is shown in the table below.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99856) BD ( 1) B 1 - H 2
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 2 s(100.00%)
1.0000 0.0001
2. (1.99856) BD ( 1) B 1 - H 3
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 3 s(100.00%)
1.0000 0.0001
3. (1.99856) BD ( 1) B 1 - H 4
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
Numbers 1-3 represent Natural Bond Orbitals between Boron and hydrogen. Boron orbitals contribute 45.36% towards the bond. These boron orbitals are 33.33% s character and 66.67% p character-and therefore is sp2 hybridised. 100% s charcter hydrogen orbitals contribute 54.64% towards the bond.
The 4th Natural Bond Orbital is 100% s character centered on boron. This is the 1s orbital that does not participate in bonding.
The 5th Natural Bond Orbital shows an s orbital on the boron atom. An empty p orbital would be expected in this case. This anomalous result may be due to the use of a low basis set.
"Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis" outlines mixing of molecular orbitals. However mixing is not significant in BH3 and therefore not alot of information is shown (below).
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
4. CR ( 1) B 1 / 10. RY*( 1) H 2 0.70 7.42 0.064
4. CR ( 1) B 1 / 11. RY*( 1) H 3 0.70 7.42 0.064
4. CR ( 1) B 1 / 12. RY*( 1) H 4 0.70 7.42 0.064
Below is a summary of the occupancy of the NBOs of BH3.
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99856 -0.43346
2. BD ( 1) B 1 - H 3 1.99856 -0.43346
3. BD ( 1) B 1 - H 4 1.99856 -0.43346
4. CR ( 1) B 1 1.99954 -6.68342 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.53893
6. RY*( 1) B 1 0.00000 0.37501
7. RY*( 2) B 1 0.00000 0.37501
8. RY*( 3) B 1 0.00000 -0.04051
9. RY*( 4) B 1 0.00000 0.41499
10. RY*( 1) H 2 0.00015 0.73289
11. RY*( 1) H 3 0.00015 0.73289
12. RY*( 1) H 4 0.00015 0.73289
13. BD*( 1) B 1 - H 2 0.00144 0.42262
14. BD*( 1) B 1 - H 3 0.00144 0.42262
15. BD*( 1) B 1 - H 4 0.00144 0.42262
-------------------------------
Total Lewis 7.99523 ( 99.9404%)
Valence non-Lewis 0.00431 ( 0.0538%)
Rydberg non-Lewis 0.00046 ( 0.0058%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
From the table above it can be seen that for each B-H bond there are 2 electrons. There are also 2 electrons in the Borons 1s orbital.
TlBr3
Calculating wavefunctions for each orbital of a compound such as TlBr3, with so many electrons, would be computationally expensive. Thus a pseudo potential is used. This is a potential used to model the core orbitals of an atom. This is because we know the core orbitals are not involved in chemical bonding.
The 3-21G basis set used previously would not suffice here-both atoms in this molecule are beyond the first row of the periodic table, making the system much more complex. Hence LANL2DZ was used to optimise TlBr3.
Optimisation
The structure was optimised using DFT-B3LYP method and LANL2DZ basis set. Its point was also constrained to D3h to ensure the right minima was reached.
Below is a summary of the optimisation.
| TlBr3 optimisation | |
| File Name | tlbr3_optimisation |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.218 +/-3.808x10-3 a.u. |
| RMS Gradient Norm | 0.000+/-3.808x10-3a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.00 Debye |
| Point Group | D3H |
Frequency Analysis
A confirmation that the minima has been reached is needed and frequency analysis does this. Frequency analysis was carried out on the optimised structure using the DFT-B3LYP and LANL2DZ basis set. It is important that the same method and basis set is used so that the results are comparable. The summary of the calculation is shown below.
| TlBr3 frequency | |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.218 +/-3.808x10-3 a.u. |
| RMS Gradient Norm | 0.000 +/-3.808x10-3 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 22.6 seconds. |
The low frequencies of TlBr3 were calculated as -3.4, 0.0, 0.0, 0.0, 3.9, 3.9
The lowest 'real' mode was found at 46.4cm-1.
Vibrational frequencies are shown below.
| Stretching mode number | Frequency(cm-1) | Intensity |
| 1 | 46 | 4 |
| 2 | 46 | 4 |
| 3 | 52 | 6 |
| 4 | 165 | 0 |
| 5 | 211 | 25 |
| 6 | 211 | 25 |
As can be seen from above no negative frequencies were recorded. This confirms that a minimum was reached.
The Br-Tl-Br bond angle was measured at 120.0o +/- 0.05o and The Tl-Br bond distance was measured as 2.65A +/- 0.005. This agrees well with the literature value of 2.6182A[3] showing that the optimised structure is reasonable and successful.
What is a bond?
Often Gaussview does not draw in bonds in certain structures. This is because it uses the relative distance of atoms compared to standard bond lengths. If the atoms are too far (cf to standard bond lengths) then the bonds are not shown.
A bond can be defined as electron density between atoms. This is a result of attractive forces between nuclei.[4] Gaussview does not consider this and is a major limitation. It may not draw the bonds but they are still there.
Cis and Trans Isomerisation of Mo(CO)4L2
In a second year experiment Mo(CO)4(PPh3)2 were synthesised. It was observed that the cis isomer showed 4 carbonyl absorption bands whereas the trans isomer showed only one. Computational chemistry would be ideal to explain this however using PPh3 as L is computationally too expensive since PPh3 is very bulky.
Hence a computationally less demanding ligand is substituted for the Ph3. For this lab it is substituted with chlorine since it exhibits similar bonding to triphenylphosphine and it is also just as sterically large. Below is the procedure of optimisation of cis and trans Mo(CO)4(PCl3)2.
Optimisation
The starting geometries used for the optimisation are shown below.
To get an initial, rough optimisation the DFT-B3LYP method was used with LANL2MB basis set. This ensures that the next optimisation occurs much more quickly.
The summary of the optimisation is shown below.
| Cis optimisation | Trans optimisation | |
| File Name | cis_output | trans_output |
| File Type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2MB | LANL2MB |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RB3LYP) | -617.53 +/-3.808x10-3a.u | -617.52+/-3.808x10-3a.u |
| RMS Gradient Norm | 0.000 +/-3.808x10-3 a.u | 0.000 +/-3.808x10-3 a.u |
| Imaginary Freq | ||
| Dipole Moment | 8.5 Debye | 0.0 Debye |
| Point Group | C1 | CI |
| Job cpu time | 13 minutes 11.5 seconds | 4 minutes 4.9 seconds |
Since the difference between the two geomteries is 2.7kJmol-1, within the error of +/-10kJmol-1 it is impossible to tell which isomer is more stable than the other.
Using DFT-B3LYP method and a more accurate basis set of LANL2DZ, the rough optimisation was made more accurate. This basis set will describe the valence atomic orbitals as well as the bonding more accurately. The summary of this calculation is shown below.
| Cis optimisation final | Trans optimisation final | |
| File Name | cis opt output | trans opt output |
| File Type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RB3LYP) | -623.58 a.u | -623.58 a.u |
| RMS Gradient Norm | 0.000 a.u | 0.000 a.u |
| Imaginary Freq | ||
| Dipole Moment | 1.31 Debye | 0.30 Debye |
| Point Group | C1 | C1 |
| Job cpu time | 17.8 seconds | 47 minutes 47.9 seconds. |
It can be seen that the 2 isomers have the same energy. However phosphorus d orbitals are not taken into account.
Frequency analysis
To ensure that both isomers were optimised to a minimum frequency analysis was carried out on them both. Below is the summary.
| Cis frequency | Trans frequency | |
| File Name | Cis frequency | Trans frequency |
| File Type | .log | .log |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RB3LYP) | -623.58 a.u | -623.58 a.u |
| RMS Gradient Norm | 0.000 a.u | 0.000 a.u |
| Imaginary Freq | 0 | 0 |
| Dipole Moment | 1.31 Debye | 0.30 Debye |
| Point Group | C1 | C1 |
| Job cpu time | 29 minutes 43.2 seconds | 31 minutes 8.8 seconds |
The energies obtained from frequency analysis are the same as the optimised energies. This confirms that the optimised structure is at a minima.
Vibrations
The results of Cis and trans vibrations (low frequencies) are shown below.
Cis isomer
| Stretching Mode number | Frequency/cm-1 | Intensity | Animation |
| 1 | 11 | 0.0 |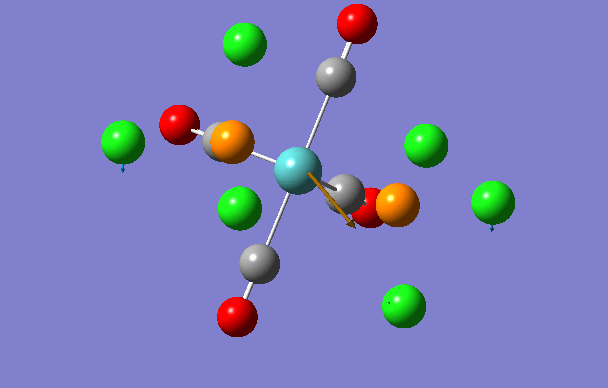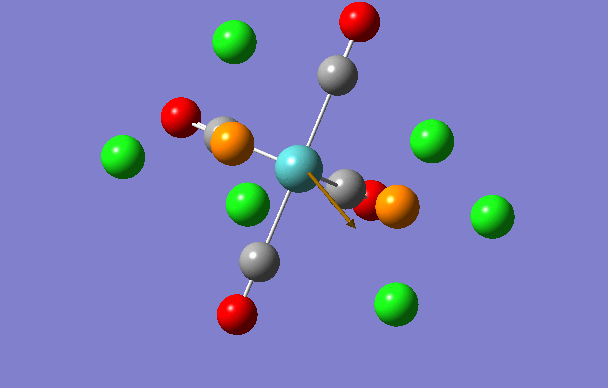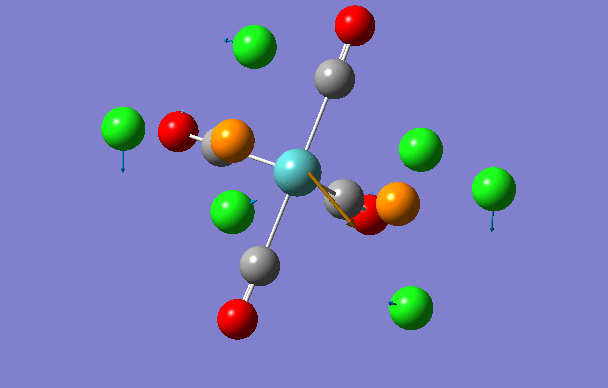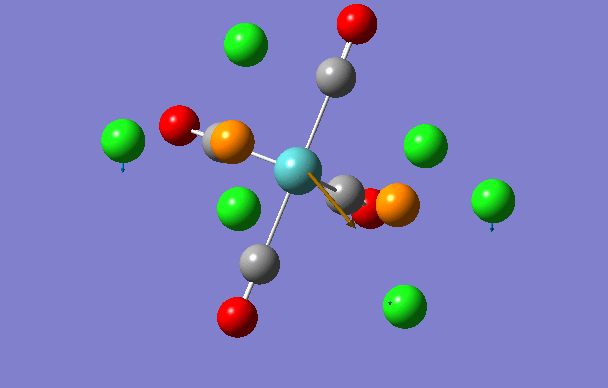 
|
| 2 | 18 | 0.0 |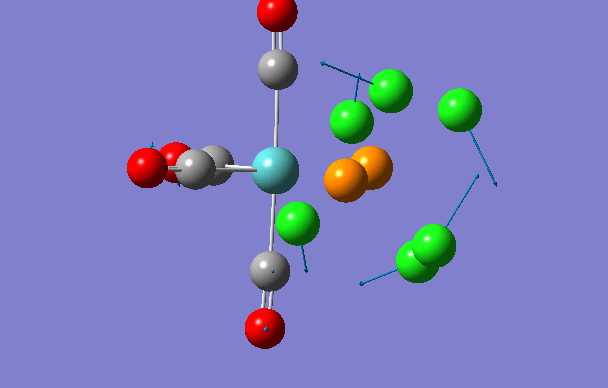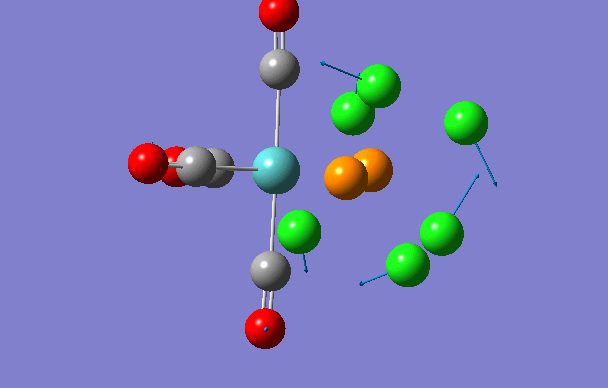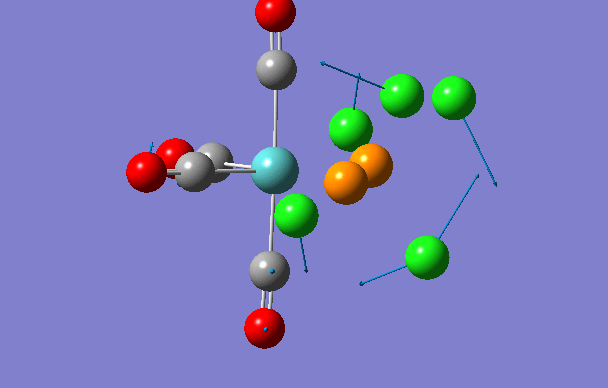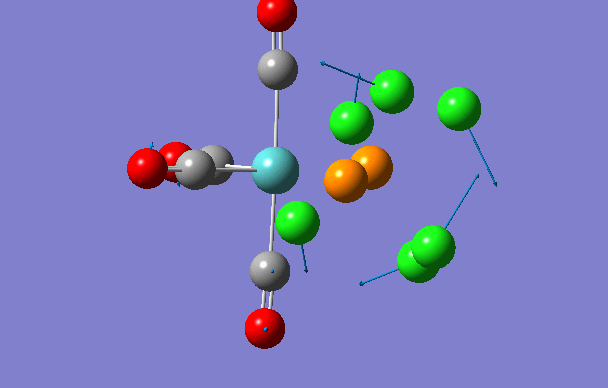 
|
| 3 | 42 | 0.0 | 
|
Trans isomer
| Stretching Mode number | Frequency/cm-1 | Intensity | Animation |
| 1 | 5 | 0.1 |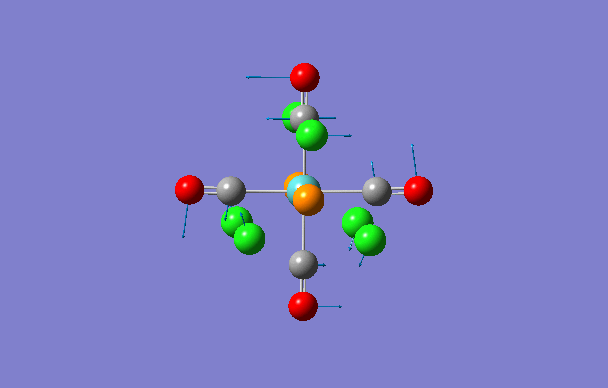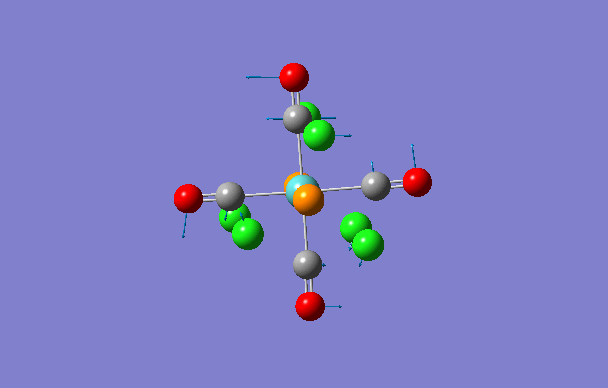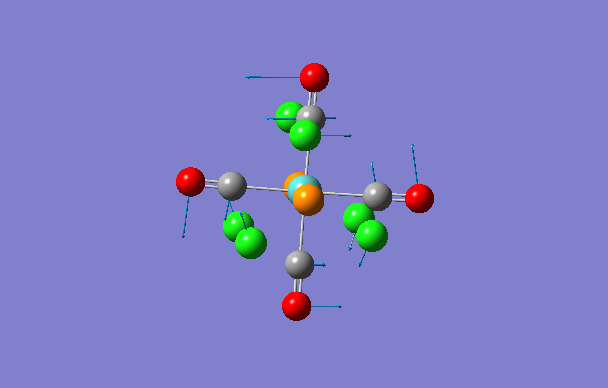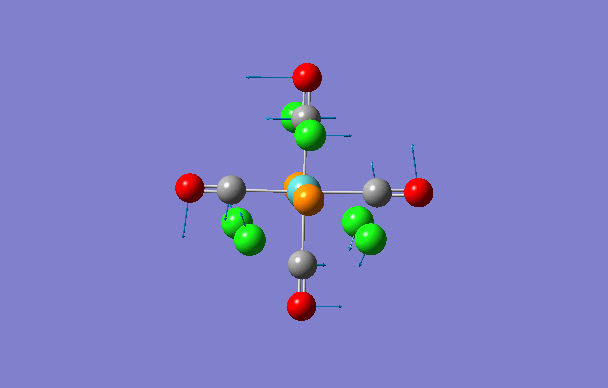 
|
| 2 | 6 | 0.0 |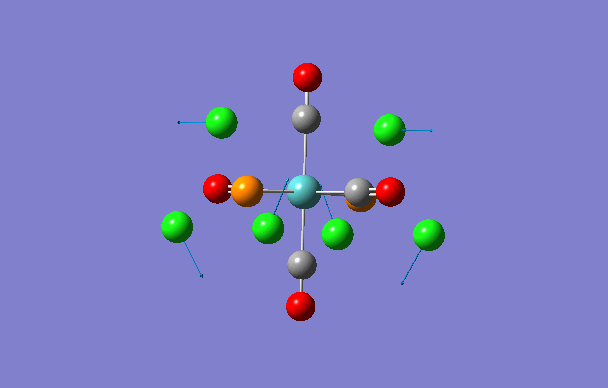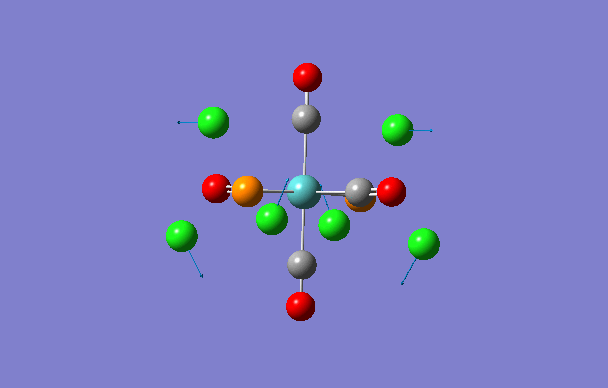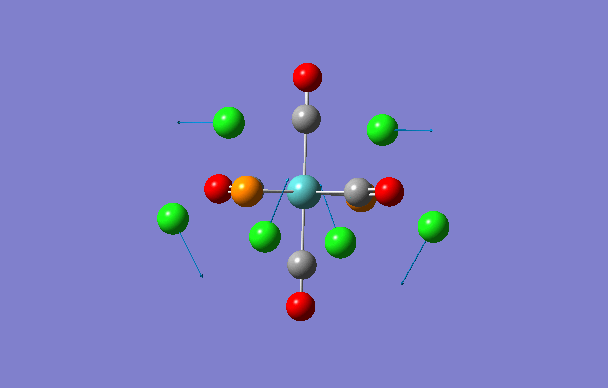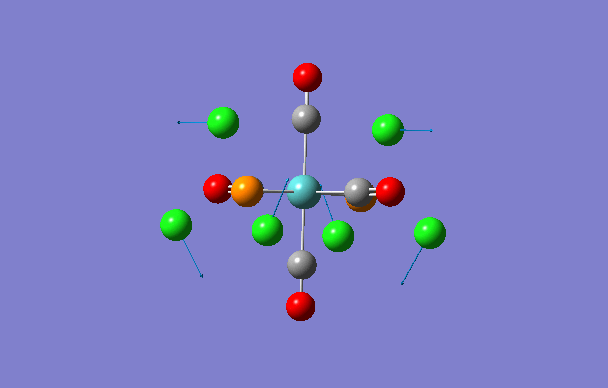 
|
| 3 | 37 | 0.4 |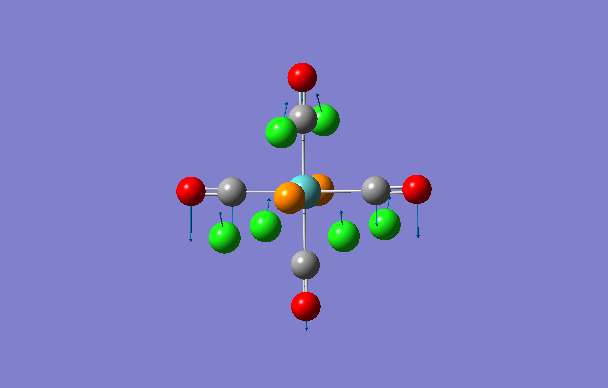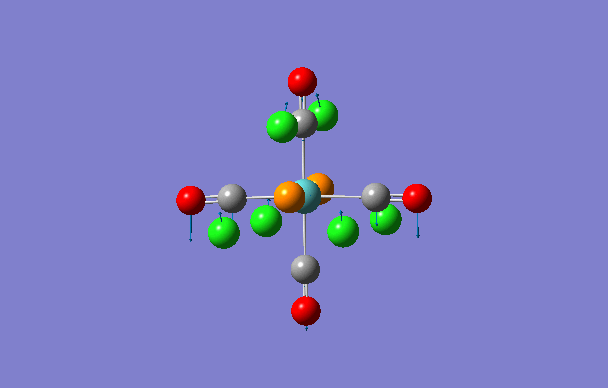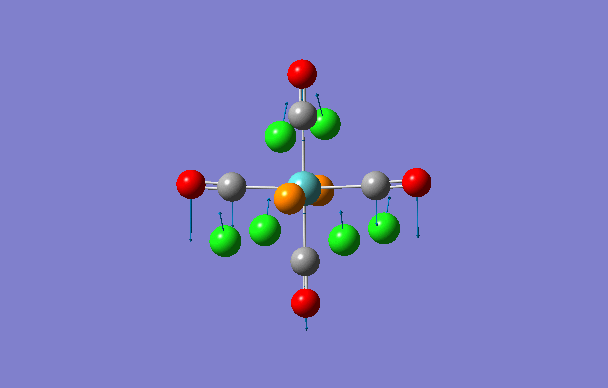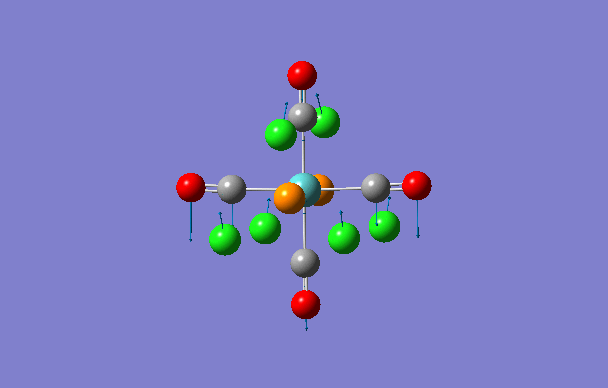 
|
Carbonyl IR stretches
Cis isomer
| Stretching Mode number | Frequency/cm-1 | Literature frequency/cm-1[5] | Intensity | Symmetry |
| 42 | 1945 | 1941 | 763 | B2 |
| 43 | 1949 | 1948 | 1498 | B1 |
| 44 | 1958 | 1965 | 633 | A1 |
| 45 | 2023 | 2049 | 598 | A1 |
Trans isomer
| Stretching Mode number | Frequency/cm-1 | Literature frequency/cm-1[5] | Intensity | Symmetry |
| 42 | 1950 | 1475 | Eu | |
| 43 | 1951 | 1467 | 1943 | Eu |
| 44 | 1977 | 1985 | 0.64 | B1g |
| 45 | 2031 | 2054 | 3.77 | A1g |
No negative frequencies were observed, confirming that the optimised structure did in fact reach a minima.
As can be seen from above 4 calculated vibrational modes are seen. However the A1g and B1g vibrational modes are of very low intensity. This because the molecule has deviations from ideal bond angles described below. It also recorded that the C-Mo-C bond angles were not measured to be the expected 90° leadig to a change in dipole moment. The EU vibrations are degenerate and thus would give one peak in the IR spectrum.
Bond angles and bond lengths
The bond lengths and angles of the cis isomer were measured and compared to literature values of cis-Mo(CO)4(PPh3)2.This comparision ensures a reasonable structure has been reached. Below are the results.
| Bond Length | Measured values for cis-Mo(CO)4(PCl3)2/A | Literature values for cis-Mo(CO)4(PPh3)2/A[6] |
| Mo-P | 2.51 | 2.58 |
| Mo-C (equatorial C) | 2.01 | 1.97 |
| Mo-C (axial C) | 2.06 | 2.02 |
| C-O (equatorial) | 1.18 | 1.13 |
| C-O (axial) | 1.17 | 1.15 |
| Bond Angle | Measured values for cis-Mo(CO)4(PCl3)2/o | Literature values for cis-Mo(CO)4(PPh3)2/o[6] |
| C-Mo-C (trans) | 178.3 | 174.1 |
| C-Mo-C (cis) | 89.7 | 90.1 |
| P-Mo-C (CO cis) | 91.9 | 91.7 |
| P-Mo-C (CO trans) | 176.1 | 173.2 |
Although comparision is not to the same structure the bond lengths and angles are reasonable for this set of literature data. It can therefore be concluded that the optimised molecule has a reasonable structure.
Steric and electronic contribution to stability. If such a small energy difference is seen there is a fine blalnce bewtween these 2 contributions.
The cis isomer would experience more steric strain which is less in the trans-complex. So steric strain favours trans-complex. However attractive interactions between ligands would favour the cis isomer.
As an electronic component the cis isomer has trans effect. This may be due to some interaction between the phosphorus lone pair and the the pi* of trans carbonyl ligand. The orbital containing the lone pair is stabilised and that of the unfilled pi* is destabilised. Overall the complex is electronically stabilised.
To access each structural isomer the magnitude of the steric and electronic components should be changed.
Mini project
Square planar vs tetrahedral
Four co-ordinate complexes of the type ML4 can adapt two geometries; square planar or tetrahedral.When ligands are brought up to the metal the relative energies of its metal orbitals change according to the symmetry of the ligand arrangement.
For d8 four coordinate complexes, square planar geometry is sometimes favoured- so long as the ligands are not so bulky as to force the complex into a tetrahedral geometry. The splitting of the d orbitals for the two geometries is very different and is shown in the image below.
For this project 2 complexes, Ni(Cl)2(PPh3)2 and Pt(Cl)2(PPh3)2 were to be computationally analysed to see which geometry was preferred. However since Ph3 are computationally demanding substituents the calculations were carried out using chlorines(shown below).
The structures were initially optimised using the DFT-B3LYP method and 3-21G basis set. This was just a rough optimisation-another optimisation, with a better basis set would be required. It is important to note that for this project it was important to constrain the symmetry and this was done for all the complexes. For the purpose of this lab we will concentrate on [NiCl4]2- in the tetrahedral conformation.
This initial optimisation for [NiCL4]2- was successful and a look at the output file showed that it converged.
The second optimisation used the DFT-B3LYP method with LANL2DZ basis set. However a look at the output file showed that it did not converge. DOI:10042/to-9967 This happened for all the structures. Although several trials were made changing various things (eg trying without constraining the symmetry) the calculation did not work. Below are some links to a few of these:
If these calculations were successful the energies would have been compared to see which geometry is more stable. These energies would also be compared to those obtained by frequency analysis to ensure a 'minima' has been reached. The molecular orbitals would have been calculated and analysis of these may explain more in depth of the preference of one geometry compared to the other. It would also have been interesting to see the results between Ni and Pt, because although they are in the same group the geometry preferences may be very different.
Dr Hunt managed to look at my files and came to the conclusion that a more in depth investigation would be required in order to understand what went wrong. It was therefore decided on Monday afternoon at 02:30pm that a new project should be looked at.
Cisplatin
Cisplatin is an anticancer drug discovered in the 1980s. Once cisplatin enters the body it undergoes hydrolysis due to the low concentration of chloride ions. This complex reacts more readily with the targets. [7] For this project the stability of cisplatin is analysed compared to trans-DDP. The hydrolysis product is also analysed.
Using the DFT-B3LYP method and LanL2DZ for Pt and Cl, 6-311G(d,p) for N and H as the basis sets. The pseudo-potential needs to be used since they are heavier atoms.
The optimisation was carried out successfully for all 4 structures, they all converged.
Frequency calculations for cisplatin were made and the same energies obtained. However, there were negative vibrations calculated. This means that on optimisation a minima was not reached. These calculations were made for trans-DDP too and here negative values were obtained too. Due to time constraints unfortunately no more analysis could be made. However, these vibrations could correspond to NH3 rocking/rotating motions.Further investigation would be needed to explain this.
References
- ↑ Frank Jensen in Introduction to computational chemistry 2007, John Wiley & Sons, 192-197
- ↑ Handbook of Chemistry & Physics 2011-2012, 92nd Edition, 9-21
- ↑ Handbook of Chemistry & Physics 2011-2012, 92nd Edition, 9-30
- ↑ Linus Pauling in The nature of the chemical bond and the structure of molecules and crystals,1960,Cornell University Press,6
- ↑ 5.0 5.1 Donald J. Darensbourg and Marcetta Y. Darensbourg,J. Chem. Educ., 1970, 47 (1), p 33. DOI:10.1021/ed047p33
- ↑ 6.0 6.1 F. Albert Cotton, Donald J. Darensbourg, Simonetta Klein, and Brian W. S. Kolthammer,Inorg. Chem., 21, (1982), p294-299. DOI:10.1021/ic00131a055
- ↑ Elizabeth R. Jamieson and Stephen J. Lippard,Chem. Rev., 1999, 99(9), pp 2467–2498 DOI:10.1021/cr980421n