Rep:Mod:ms mod1
Module 1: Modelling with molecular mechanics
Molecular Mechanics is a parametric method used as to estimate energies and their contributions by taking a weighted average of known functional values. It has very many limitations, where in its calculations it does take into account stereoelectronics, hyperconjucation, molecular orbitals, just to name a few.
The Hydrogenation Of Cyclopentadiene Dimer
Dimerisation Of Cyclopentadiene: Endo/Exo selectivity
Cyclopentadiene is a product of petroleum cracking. It has a wide array of uses in chemistry; from catalysts to hydrocarbon resins. Cyclopentadiene dimerises in a Diels-Alder reaction at room temperature. One molecule reacts as the diene and the other as a dienophile to form dicyclopentadiene. [1]
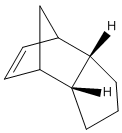
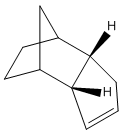
Two diastereoisomers can form from this dimerisation; the exo isomer (1) and the endo isomer (2).
Jmol for structure (1)
Jmol for structure (2)
One of these diastereoisomers is more preferable as the thermodynamic product of this reaction, while the other as a kinetic product. The thermodynamic product is the lowest energy product, while the kinetic product is the most easily formed product (most stable transition state). Conditions that give rise to thermodynamic and kinetic products are called thermodynamic control and kinetic control respectively.[2]
Thermodynamic control[3]: Equilibrium reached rapidly. Difference in activation energies for forward and reverse reactions is equal to change in energy from starting material to product.
Kinetic control [3]:Reverse reaction cannot occur (or is very slow). Product mixture is dependent upon the rates of the competing processes. Preference for one product over another is predisposed with relative heights of the activation energy barrier for the two processes, i.e the lowest transition state barrier.
Using the MM2 force field option the thermodynamic product was found by comparing molecular energies of geometrically optimized final product conformations (since the thermodynamic product is the lowest energy product). Below is a table comparing the values obtained for the respective contributions.
Exo-dimer(1) Endo-dimer (2) Stretch: 1.28 1.25 Bend: 20.58 20.85 Stretch-Bend: -0.84 -0.84 Torsion: 7.65 9.51 Non-1,4 VDW: -1.42 -1.54 1,4 VDW: 4.23 4.32 Dipole/Dipole: 0.38 0.45 Total Energy(kcal/mol): 31.88 34.00
From the above data it can be seen that the exo dimer (1) is thermodynamically more stable than the endo dimer (2) by 2.12 kcal/mol. This can be explained because of the torsional strain the endo dimer experiences. There is repuslion between atoms located in a 1,4 relationship in the endo isomer which is not present in the exo isomer. This strain is shown in Figure 1 below.
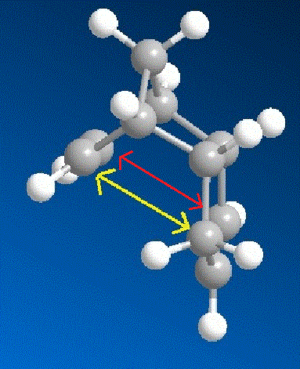
Although the endo dimer is thermodynamically less stable it is formed preferentially. [4] This tells us that the exo dimer is only the thermodynamic product; the endo isomer is the kinetic product and is converted to the exo isomer at higher temperatures. Hence the endo product has a low energy transition state. If transition state energies of two geometrically optimized transition conformations were caluclated this would have been evident.
To understand why the transition state of the endo isomer is lower in energy than that of the exo isomer frontier molecular orbitals need to be taken into account.
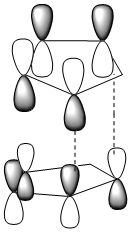
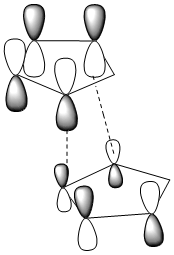
Note: Dotted lines represent sigma bond formation
It can be seen that the endo transition state has additional overlap (of the HOMO and LUMO) which is not present in the exo tranisition state. This additional overlap is the reason for stability of the endo transition state.
The Hydrogenation Of Endo Dimer Of Dicyclopentadiene
Since the endo dimer is the kinetic product, it will be the isomer that is hydrogenated. Initially dihydrodicyclopentadiene is formed, and then with further hydrogenation endo-tetradicyclopentadiene is obtained.[5] In the formation of dihydrodicyclopentadiene there are 2 possible alkenes that can be hydrogenated. Structure (3) and (4) below are the possible products after hydrogenation.
Jmol for structure (3)
Jmol for structure (4)
(3) (4) Stretch: 1.28 1.10 Bend: 19.87 14.53 Stretch-Bend: -0.83 -0.55 Torsion: 10.80 12.50 Non-1,4 VDW: -1.22 -1.07 1,4 VDW: 5.63 4.51 Dipole/Dipole: 0.16 0.14 Total Energy(kcal/mol): 35.69 31.15
From the table above it can be seen that structure (4) is more stable than structure (3) by 4.54 kcal/mol. This can be explained due to angular strain. This angle is between the double bond and a substituent of the alkene. This was measured as 109.81o for structure (3) and 112.80o for structure (4). Ideally the angle of an alkene should be 120o as the caron is SP2 hybridised. Any values that differ from this will cause angular strain and hence it can be said that structure (3) experiences larger angular strain than structure (4) as its deviation from the ideal bond angle is much larger.
Structure 4 is in fact the one formed preferentially [6] and is also the thermodynamic product. However, modelling of the transition state would be required to determine if the hydrogenation reaction is under thermodynamic or kinetic control. Molecular mechanics cannot do this-examination of orbitals involved is needed.
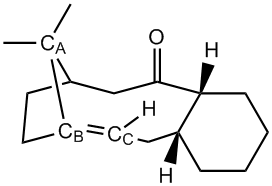
Stereochemistry and Reactivity of an intermediate in the synthesis of Taxol
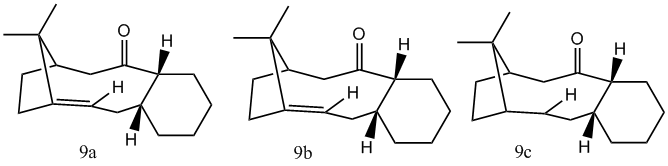
During the synthesis of Taxol, used in the treatment of cancer, a key intermediate is formed. In this intermediate the carbonyl group may point either up (9) or down (10). On standing, the compound isomerises to the alternative carbonyl isomer.[7] Hence it can be concluded that in the formation reaction of the key intermediate the kinteic product is initially formed which converts to the thermodynamic product. Performing molecular mechanic calculations will help us determine energies of the isomers and thus which isomer is the kinetic one and which is the thermodynamic.
Jmol for 9a-the intermediate in the synthesis of taxol with cyclohexyl ring in a chair conformation.
Jmol for 9b-the intermediate in the synthesis of taxol with cyclohexyl ring in a twist-boat conformation.
Jmol for 9c-the hydrogenation product of 9a
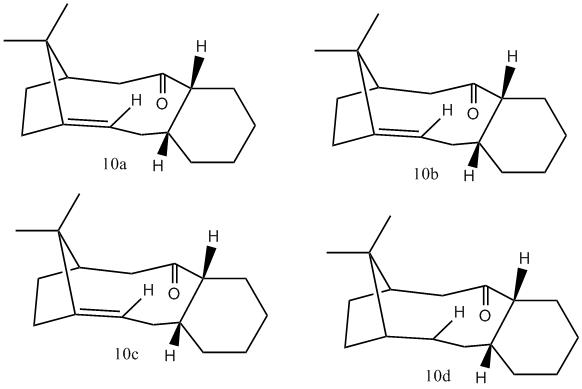
Jmol for 10a-the intermediate in the synthesis of taxol with cyclohexyl ring in a chair conformation. The carbon-carbon bond at the bridge pointing down.
Jmol for 10b-the intermediate in the synthesis of taxol with cyclohexyl ring in a chair conformation. The carbon-carbon bond at the bridge pointing up.
Jmol for 10c-the intermediate in the synthesis of taxol with cyclohexyl ring in a twist boat conformation.
Jmol for 10d-the hydrogenated intermediate of product 10a.
Below is a table of total energies calculated using MM2 and MMFF94 force field minimisation.
9a(Chair) 9b (Twist boat) 10a(C-C down) 10b(C-C up) 10c(twist boat) MM2(kcal/mol) 47.84 53.01 42.68 52.54 46.45 MMFF94 (kcal/mol) 70.55 75.93 60.55 74.79 66.80
Note: It was observed that the cyclohexyl ring had 2 possible conformations; the preferred chair and the twist boat.
From the table above it can be seen that the MMFF94 calculations have a similar trend in energies as the MM2 results. However the energies cannot be compared directly as the the 2 differ in their method of calculations (eg different parameters). It can also be seen that for intermediate 10 there are 2 chair conformations. From these 2 conformers 10a is the lowest energy conformer and hence the thermodynamic product. It is therefore possible that structure 9 is initially formed and converts to 10 upon standing.
The energy contributions to the total energy were analysed to help explain why the reaction of the alkene was slow. This was done for the intermediate 9a and 10a and their corresponding alkanes. This comparision seems reasonable for the further functionalisation as when an alkene reacts in an electrophilic addition reaction, hybridisation changes from sp2 to sp3. Below is the table summarising the energy contributions.
Energies (kcal/mol) 9A (chair) 9c(alkane chair) 10a(chair front down) 10d (alkane chair) Stretch 2.78 2.88 2.62 2.52 Bend 16.54 17.28 11.34 15.32 Stretch-Bend 0.43 0.47 0.34 0.62 Torsion 18.25 20.61 19.67 22.80 Van der Waals 13.11 14.38 12.87 16.51 Dipole-Dipole 0.13 0.05 -2.00 0.03 Total 47.84 53.01 42.68 52.52
From the above data it can be seen that 9a and 10a are more stable than their corresponding alkane (9c and 10d). To interpret this stability of bridgehead olefins, the olefinic strain energies are obtained. This is calculated as the difference between the total energy of the olefin in its most stable conformation and the total energy of the saturated hydrocarbon (alkane). [8] The olefin strain energies for 9 and 10 are calculated to be -5.17 kcal/mol and -9.84 kcal/mol respectively. Alkenes that have a negative olefin strain energies are classed as hyperstable olefins. [9]
From the table above it can be seen that Torsion and Van der Waals contributions are the main components of these olefin strain energies. Below is a a diagram of intermediate 9 to help explain these contributions.
Alkenes are sp2 hybridised and have an ideal bond angle of 1200. On the other hand alkanes are sp3 hybridised and have an ideal bond angle of 109.50. For the alkene and alkane the bond angles were measured as 1220 and 1180 respectively. The alkane shows largest deviation from the ideal bond angle and thus experiences more torsional strain.
Van der Waals interactions was the other major contribution to the olefin strain energy. This interaction was calculated using a Leonard Jones 6-12 potential. The potential shows us that for H-H interactions the function is repulsive at around 2.1Å and attractive around 2.4Å. The close contacts between atoms in the alkane and alkene structures was calculated. The alkene structure showed one less repulsive Van der Waals interation than the alkane. These interactions are shown in the diagram below.

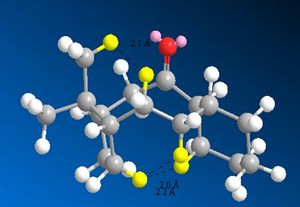
From these diagrams it can be concluded that H-H repuslive interactions (transannular strain) are also a reason for the hyperstability of the alkene. There is an additional repulsive term when going from an alkene to an alkane hence raising the latters energy. This, and increased angular strain, are the reason of the slow reactivity of the alkenes 9 and 10.
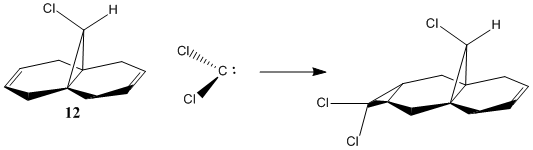
Regioselective Addition Of Dichlorocarbene
Orbital Control
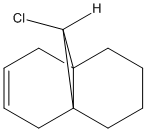
Chlorocarbenes have an electron deficient nature and thus are very reactive electrophilic reagents. They react with alkenes via a cycloaddition mechanism forming cyclopropanes. Dichlorocarbene reacts regioselectively with compound 12, proven experimentally.[10]
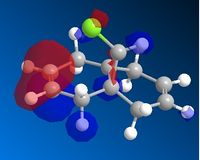
Compound 12's geometry was optimised using MM2. It was the optimised and molecular orbitals calculated with MOPAC using the PM6 method. This is because, as seen above, molecular mechanics cannot handle molecular orbitals or transition states. Below is a figure of the HOMO. It can be seen it is not symmetric.
AS the molecule has CS symmetry, the orbitals should show CS symmetry. As can be seen from the image above the PM6 method gives non symmetrical orbitals. Therefore the calculations were carried out using RM1. Below are the results.
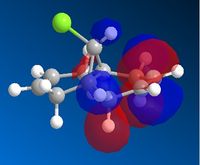

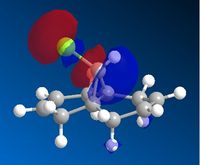
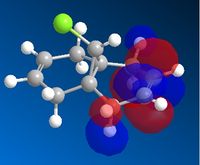
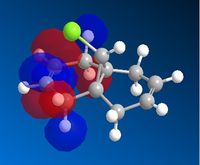
It can be seen that the HOMO lies on the alkene endo to the C-Cl bond. Regioselectivity is now apparent. It is usually assumed that two π orbitals are of similar energy and therefore equally nucleophilic. Experimentally however this is not seen. The π orbital exo to the C-Cl bond can overlap with the σ* orbital of the C-Cl bond.
This interaction stabilises the exo π orbital and is possible due to correct orientation and orbitals being similar in energy.The σ* of C-Cl bond is a low lying empty orbital (due to electronegativity of chlorine) and the pi orbital of the C-C bond is a high lying filled orbital. The exo pi orbital becomes energitically more stable and therefore less nucleophilic. Hence nucleophilic attack occurs from the endo pi orbital.
Vibrational Energies
The influence of the Cl-C bond on vibrational frequencies was analysed. This was done using MOPAC/RM1.The results are compared to the monohydrogenated derivative (structure 13). Below are the results.
Wavenumber/cm-1 Bond Structure 12 Structure 13 C-Cl 770.81 774.96 C=Cendo 1757.44 1758.06 C=Cexo 1737.07 N/A
Only one C=C stretch is observed for structure 13. This is due to the double bond endo to the C-Cl. This C=C cannot overlap with the C-Cl σ* (no secondary orbital overlap effects).
To analyse the IR of structure 12 it is best to compare the sretching energies with those of structure 13 .The C-Cl stretch occurs at a lower energy (770.81) compared to that of structure 13(774.96). This is due to donation into with the C-Cl σ* from the exo π orbital which is present in 12 and not 13. This donation leads to a more delocalised and diffuse orbital character between the 2 carbons resulting in a weaker bond. The endo C=C stretching energies are similar for both structures (1757.44 compared to 1758.06).
The endo C=C bond is more nucleophilic than the exo C=C bond because its π orbital is more localised and higher in energy. As previously explained this is due to overlap of the exo C=C π orbital with the σ* C-Cl orbital.
Monosaccharide Chemistry: Glycosidation
D-glucose is the most important monosaccharide; it is the building block of many other carbohydrates. The chemistry of D-glucose is similar to that of aldehydes/ketones and alcohols. Hence cyclisation occurs and D-glucopyranose is formed.
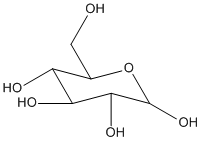
During monosaccharide chemistry, protecting groups are used to mask the reactivity of one or more functional gorups in the molecule whilst allowing the modification of another functional group in the same molecule.
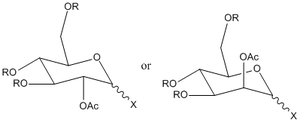
Figure 2 above shows the D-glucose derivative we will focus on in this section. The glycosidation, of this process where group X is replaced by a nucleophile Nu, will be analysed. The 2 sugars in Figure 2 above give different anomers during this process. This is dependent on the orientation of the OAc group (Figure 3 below) and is called the neighbouring group effect. The carbonyl on the acetyl stabilises the oxonium ion and hence blocks one face. The nucleophile attacks from the other face making the mechanism stereospecific.
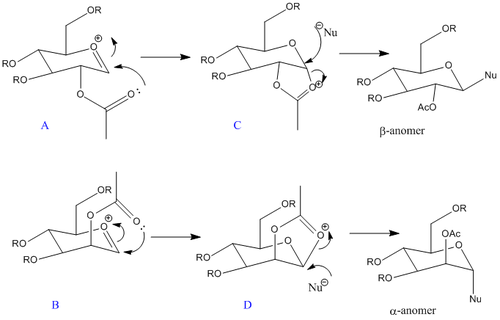
Using MM2 and the MOPAC/PM6 methods, these facial preferences (diastereospecificity) were analysed with respect to their energies. Although hydrogen as an R group would keep the computational demand lower it is actually not a protecting group and hence the chemistry of the molecule would be compromised. These calculations were tried with acetyl as the R group too however energies were higher and the computaional demand was quite high too. Hence methyl was deemed the suitable R group. A was compared to B and C to D. It was discovered that each of these structures had isomers. Hence A', B',C' and D' were also analysed. A' and B' correspond to the isomer where the oxygen on the acetyl group is out of the plane. Below are the optimization results.
A A' B B' Stretch: 2.52 2.33 2.37 2.42 Bend: 11.20 10.48 11.29 19.57 Stretch-Bend: 0.96 0.91 0.97 1.18 Torsion: 0.34 0.58 2.08 0.48 Non-1,4 VDW: -1.28 -2.77 -1.63 -1.50 1,4 VDW: 18.21 18.30 18.55 17.08 Charge/Dipole: -12.98 -4.44 -13.03 -2.80 Dipole/Dipole: 5.50 4.74 4.96 5.10 Total Energy(kcal/mol):24.47 30.13 25.54 41.52 MOPAC/PM6(kcal/mol): -91.73 -77.18 -88.73 -66.00
Jmol for A
Jmol for A'
Jmol for B
Jmol for B'
Using the MM2 calculations it can be seen from the data above that overall of A and A' are more stable than B and B' respectively. It can also be seen that A and B are more stable than their corresponding isomers A' and B'. This is because A' and B' have the carbonyl on the acetyl out of the plane, hence the oxonium ion is not stablised by the carbonyl. Therefore higher energy is seen for both.
The reason for A being more stable than B is again the interaction of the carbonyl on the acetyl with the oxonium ion. In A the carbonyl is in the right orientation for the interaction hence stabilises the oxonium ion, therefore lowering the energy of the molecule. This is not present in B since the carbonyl is not in the right orientation for this stabilisation effect to take place.
The MOPAC/PM6 results follow the same trend as the MM2 results since the energies of both isomers of A are lower in energy (more negative) than those for B. However the 2 methods are not comparable as they perform the calculations by taking different parameters into account. For this calculation MOPAC is in fact the better method as it takes molecular orbitals into account.
The same calculations were carried out for C, C', D and D'. Structure C' and D' can be described as the bonded structure of A' and B'. Below are the results.
Jmol for C
Jmol for C'
Jmol for D
Jmol for D
C C' D D'
cis-fused trans-fused cis-fused trans-fused
Stretch: 1.78 2.64 2.09 2.65
Bend: 14.59 17.52 14.60 16.94
Stretch-Bend: 0.65 0.82 0.70 0.75
Torsion: 7.24 8.12 9.36 7.65
Non-1,4 VDW: -4.03 -3.14 -3.33 -2.92
1,4 VDW: 17.97 19.42 18.34 19.36
Charge/Dipole: -3.13 -1.88 -7.95 3.10
Dipole/Dipole: 0.54 0.25 -0.54 -0.75
Total Energy(kcal/mol):28.63 43.74 33.28 46.78
MOPAC/PM6(kcal/mol): -91.66 -77.84 -88.54 -66.67
As above the results from MOPAC and MM2 are not comparable however they show a similar trend. Overall both isomers for C have lower energies than the isomers of D. This can be explained by the anomeric effect.
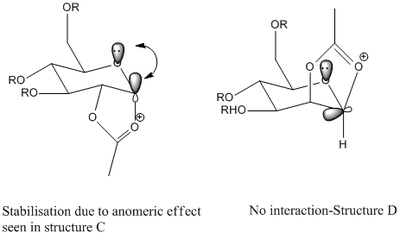
Anomeric effect: Stabilisation of axial substituent via donation into C-O σ* orbital by the lone pair on the oxygen in the ring(Figure 4 below). This is a form of hyperconjugation.
This effect is not present in B since the acetyl is bonded as an equatorial substituent.
Bond angles and bond lengths were analysed for the 2 methods for C and D. Below are the results:
MOPAC MM2
C C' D D' C C' D D'
Bond Length(A) 1.3 1.4 1.3 1.4 1.4 1.4 1.4 1.4
Bond Angle(0) 105 112 106 113 108 122 114 122
The bond angle was measured between the oxygen on the acetyl, and the oxygen in the ring. The bond length calculated was that between the oxygen in the ring and the adjacent carbon where the acetyl attaches. It can be seen that both methods give similar and consistent bond lengths but MOPAC minismises the angles considerably. This is why MOPAC is the preferred modeling method.
C' and D' are alot higher than C and D because they are trans-fused and therefore much more strained making them energetically less favourable. If C is the most stable isomer then why is the beta-anomer not the preferred one? The Curtin-Hammet principle can explain this. It states that 'the ratio of products is determined by relative heights of the highest energy barriers (difference in free energy of the transition state) going to each product, and not on the equilibrium constant between the intermediates'. [11] This, and the anomeric effect, explains the high diastereospecificty.
Structure based Mini project using DFT-based Molecular orbital methods
The total synthesis of (-)Cubebol[12]
(-)-Cubebol (1) is is a natural sesquiterpene found in cubebob oil. It was patented as a cooling and refreshing agent in 2001.

Cubebol |
Jmol for (-)-Cubebol (1)
In this section the spectroscopic properties reported in the paper are tested and a check that data is correctly assigned.
IR vibrations
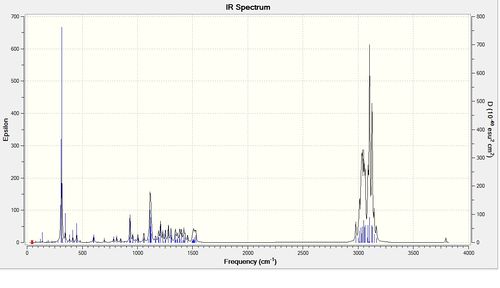
| IR frequencies | ||
| Bond | Cubebol | Literature |
| O-H stretch | 3794 | 3350 |
| C-H stretch | 2951 | 2977 |
| 1490 | 1494 | |
| C-C stretch | 1142 | 1162 |
The predicted wavenubers are systematically too high for stretches by around 8%. Taking this into account it can be seen that the modeled method agrees well with literature values.
13C NMR
| Carbon | Chemical Shift | ' | ' | ' |
| (-)-Cubebol (1) | Literature | 4-epi(1) | Lierature | |
| C-4 | 79.5 | 80.3 | 77.6 | 80.8 |
| C-7 | 42.5 | 44.1 | 41.58 | 44.6 |
| C-5 | 37.5 | 39 | 36.4 | 39.9 |
| C-3 | 38.1 | 36.3 | 37.3 | 36.6 |
| C-11 | 35.1 | 33.6 | 35 | 34.9 |
| C-1 | 34.0 | 33.4 | 33 | 31.8 |
| C-9 | 34.9 | 31.7 | 34.5 | 30.2 |
| C-10 | 32.9 | 30.8 | 32.9 | 29.7 |
| C-2 | 32.1 | 29.5 | 31.6 | 29.7 |
| C-15 | 27.5 | 27.9 | 29.8 | 27.1 |
| C-8 | 26.2 | 26.4 | 26.5 | 25.3 |
| C-6 | 26.8 | 22.6 | 25.2 | 25.0 |
| CMeMe | 21.8 | 20.1 | 21.6 | 20.1 |
| CMeMe | 22.6 | 19.6 | 21.1 | 19.2 |
| CHMe | 21.6 | 18.7 | 20.6 | n/a |
DOI:10042/to-9548 for cubebol and DOI:10042/to-9549 for its epimer.
As can be seen from the table above the data obtained from the DFT method matches reasonably well with literature. The calculated shifts are with the expected 2-5ppm deviation from literature. The largest deviation is about 4ppm for the isomer of cubebol. From the data above it can be seen that the paper does in fact have the right data and correct assignments. However this method is not accurate and reliable. This is due to the inability of the model to reflect equivalence via free rotation about sigma bonds. This results in carbons that should be equivalent being treated as inequivalent and the chemical shift is not averaged across both signals.
3JH-H couplings
There is only one coupling reported in the paper(d,J=1.0 Hz, 3 H, H-15). However, it states that this coupling occurs at at H-15. This cannot be true as the nearest hydrogen to couple to is 4 bonds away, and this coupling would not be seen. The only reasonable coupling of 3 hydrogens that would produce a doublet is for that at H-14. So it is assumed that the coupling value given in the paper corresponds to this. When calculated a coupling constant J=6.0Hz was obtained. This is very large and very different from the literature one. Hence it may be that this data is wrong all together.
References
- ↑ K. Weissermel, HJ Arpe in Industrial Organic Chemistry 2003, WILEY-VCH, 125-126
- ↑ F. A. Carey, R.J. Sundberg, Advanced Organic Chemistry: Structure and Mecahnisms 2007, Springer Science, 285-286
- ↑ 3.0 3.1 J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry 2001, Oxford University Press, 328-331
- ↑ J.E Baldwin, Journal of Organic Chemistry, 1966, 2441-2444, DOI:[https://doi.org/ 10.1021/jo01346a003 10.1021/jo01346a003 ]
- ↑ Guozhu Liu, Zhentao Mi, Li Wang and Xiangwen Zhang, Ind. Eng. Chem. Res., 2005, 3846-3851, DOI:[https://doi.org/10.1021/ie0487437 10.1021/ie0487437 ]
- ↑ F. Alonso and M.Yus, J.Org.Chem, 1986, 838-841, DOI:[https://doi.org/10.1021/jo00356a016 10.1021/jo00356a016 ]
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ Eric V. Anslyn, Dennis A. Dougherty in Modern Physical Organic Chemistry 2006, University Science Books, 139
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891. DOI:[ http://dx.doi.org/10.1021/ja00398a003 10.1021/ja00398a003]
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ D. Nasipuri, Stereochemistry of Organic Compounds: Principles and Applications 2005, New Age International, 348
- ↑ K. Mori, The Chemical Record, 2005, ii5, 1-16. DOI:10.1002/tcr.20030