Rep:Mod:ms7109 module2

Structure and Bonding of Inorganic Complexes

MO analysis of BH₃

---

Geometry Optimisation

The general method to optimise a molecule involves solving the Schrodinger equation for the electron density and energy at a given position of the nuclei (SCF). Under the Born-Oppenheimer approximation the momenta of the nuclei is neglected due to their slow speed relative to electrons, thus their position is repetitively changed and the process above repeated until the lowest energy geometry is identified, this will be the minimum on a potential energy surface curve.

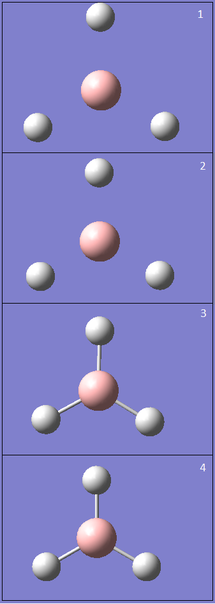
On gaussview the molecule is drawn and its geometry altered to B-H bond lengths of 150 pm. The optimisation calculation is set up to a B3LYP model, this determines the approximations in solving the Schrodinger equation, and a low accuracy but fast 3-21G basis set.

Figure 1 Confirmation of successful optimisation

Summary of Optimisation Results
B-H Bond Length	1.19Å
H-B-H Bond angle	120.0°
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	3-21G
Spin	singlet
Final Energy	-26.46 a.u.
Gradient	2.07 x 10-4 a.u.
Dipole Moment	0.00 D
Point Group	D3h
Time taken for calculation	7 s

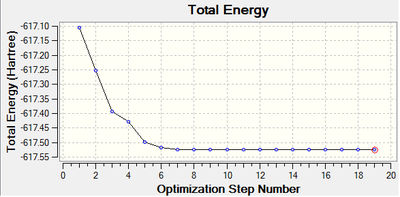
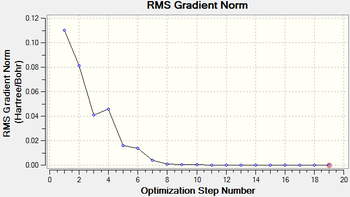
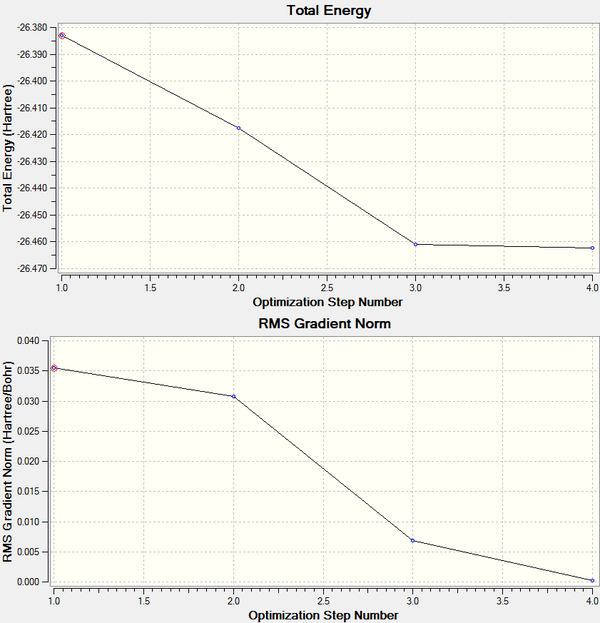
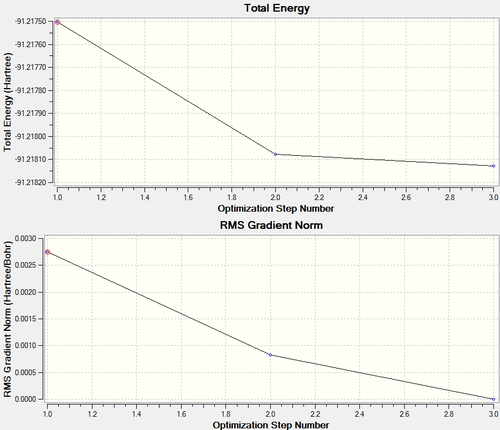
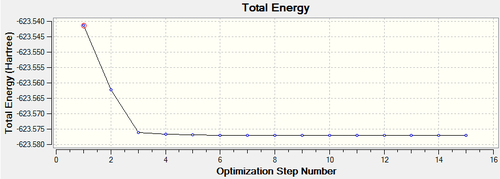
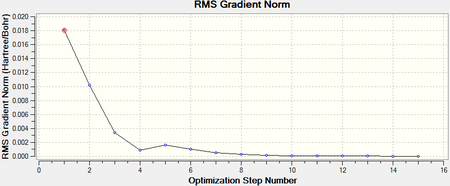
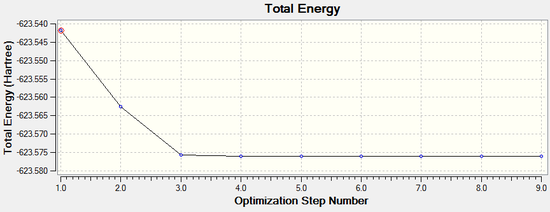
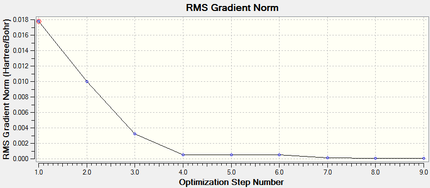
The root mean square gradient is the rate of change of total energy with respect to displacement of each atom in the x, y and z directions, in other words if the position of the nuclei is given as coordinate R and the energy as E(R), the gradient is equal to dE(R)/dR. To check that the optimization has successfully been completed the gradient should be tending to zero or at least be lower than 0.001, another way is to open the original text based .log file and assess the convergence of Forces and Displacements. Both confirm that the molecule has been optimised as the gradient < 0.001 and all convergence outcomes are YES (Fig. 1). Further analysis of the optimisation reveals that it underwent 4 iterations, starting from the least stable geometry of -26.382 a.u. and reaching what looks to be a minimum for the fourth optimisation step number (Fig. 2).

Figure 2 Total energy and RMS gradient norm optimisation curves

Figure 3 Optimised geometries of the four iterations

Nonetheless, the stationary point could still be a maximum, therefore there is a need to calculate the second derivative d²E(R)/dR² which is given by the sign in the vibrational frequencies.

---

Vibrational Analysis

To determine the vibrational modes of the BH₃ molecule a similiar calculation to that of the optimisation is carried out. B3LYP and 3-21G are used as the method and basis set respectively thus keeping the accuracy and energies analogous to the previous part.

Figure 4 IR spectrum of BH₃

Summary of Frequency Results
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	3-21G
Spin	singlet
Final Energy	-26.46 a.u.
Gradient	2.07 x 10-4 a.u.
Dipole Moment	0.00 D
Point Group	D3h
Time taken for calculation	15 s

Vibrational number	Frequency (cm-1)	Intensity	Vibrational mode	Form of vibration	Symmetry D3h point group
1	1144	92.9	Wagging, the H atoms move in a concerted motion in the positive z direction while the Boron atom moves in the opposite negative direction		A2
2	1204	12.3	Scissoring, two hydrogen atoms move up and down the xy plane making the H-B-H bond angle between them expand and contract in reverse to the other angles		E'
3	1204	12.3	Rocking, One H-B-H angle is constant making two hydrogen atoms rock while the third swings from one side to the other so as the remaining angles increase and decrease in turns		E'
4	2598	0.0	Symmetric Stretching, all B-H bonds increase simultaneously unvarying H-B-H angles and keeping the boron atom stationary.		A'1
5	2737	103.7	Asymmetric Stretching, two B-H bonds lengthen and shorten asymetrically while the third stays constant. Boron sways opposite to the most stretched H atom.		E'
6	2737	103.7	Asymmetric Stretching, two B-H bonds stretch and contract together while the third imitates them out of time. Again, boron moves slightly towards the least stretched H atoms.		E'

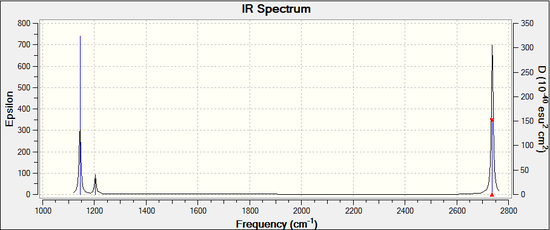
The summary for the frequency calculation shows that a D_3h point group (trigonal planar) is preserved and the final energy of the molecule is equivalent to the optimised one at -26.46 a.u. From the table above it is clear that all frequencies are positive and the stationary point during optimisation must be a minimum. All molecules have 3N-6 degrees of vibrational modes, in this case there are 4 atoms therefore BH₃ will have 3(4)-6 = 6 vibrational modes as calculated, however, one has to consider which are IR active. Only the modes associated with a change in the dipole will be detected by IR spectroscopy, as a result symmetric stretching (vibration number 4) will not come up in the spectrum due to a retention of symmetry. In addition, scissoring (2) and rocking (3) occur at identical energies in the same way as asymmetrical stretches, these are termed degenerate modes generating a single IR absorption. The spectrum in figure 4 demonstrates the presence of 3 peaks: a medium one at 1144.2 cm^-1 for wagging, a weak one at 1203.6 cm^-1 for the degenerate scissoring and rocking and a final strong peak at 2737.4 cm^-1 originating from asymmetric stretching. An advantage of using computational IR characterization is that it determines all vibrational modes whereas experimental spectroscopy gives you a less informative spectrum containing only IR active modes.

---

Molecular Orbital Diagram

A convenient outcome of computationally solving electron density is the resulting Molecular Orbitals. These are calculated quantitatively and can be compared to the approximate molecular orbitals by evaluating their corresponding MO diagrams. Once more the same B3LYP method and 3-21G basis set are used, this time running an energy calculation specifically asking for MO analysis and generating full NBO's. DOI:10042/to-10982

Figure 5 Energies of the calculated molecular orbitals, HOMO and LUMO are highlighted

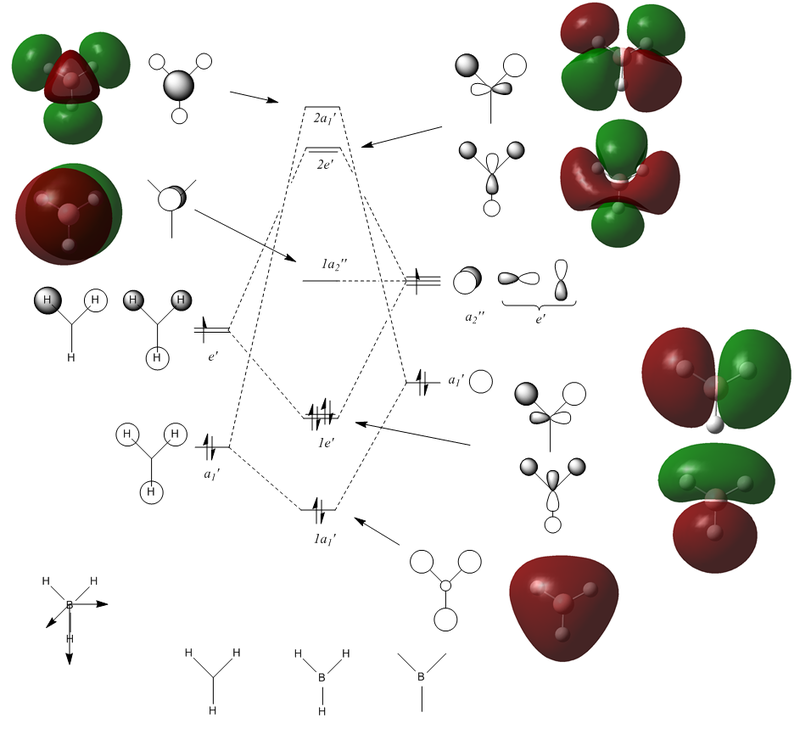Molecular orbital 1 in figure 5 is not shown in the diagram because its energy is too low whereas MO's 9 and above are also not shown since they are not significant in the bonding. Compared to the qualitative MO diagram there is one major difference, this is the position of the 2e' (6 and 7) and 2a₁' (8) orbitals which swap around when computed. Nonetheless, the graphical MO's match very well with the LCAO MO's suggesting that qualitative MO theory is very useful when describing simple molecules but would be too difficult for more complex ones.

---

Natural Bond Orbitals analysis

NBO's help to determine the most accurate Lewis structure of BH₃ or what is more commonly known as the 2c-2e bonding picture with the electron density localized on atoms and bonds. Gaussview can only give a graphical representation of charge distribution but the original .log file entails a lot more such as hybridization or orbital mixing.

Summary of Natural Population Analysis: Natural Population Natural ----------------------------------------------- Atom No Charge Core Valence Rydberg Total ----------------------------------------------------------------------- B 1 0.33161 1.99903 2.66935 0.00000 4.66839 H 2 -0.11054 0.00000 1.11021 0.00032 1.11054 H 3 -0.11054 0.00000 1.11021 0.00032 1.11054 H 4 -0.11054 0.00000 1.11021 0.00032 1.11054

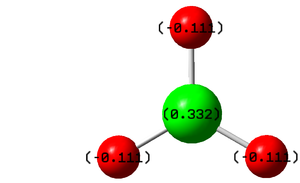
The diagram and the table above inform us about the charge distribution in BH₃, Boron is highly positively charged reflecting its Lewis deficient character whilst the hydrogen atoms are negatively charged holding a third of the charge each.

(Occupancy) Bond orbital/ Coefficients/ Hybrids --------------------------------------------------------------------------------- 1. (1.99853) BD ( 1) B 1 - H 2 ( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%) 0.0000 0.5774 0.0000 0.0000 0.0000 0.8165 0.0000 0.0000 0.0000 ( 55.52%) 0.7451* H 2 s(100.00%) 1.0000 0.0000 2. (1.99853) BD ( 1) B 1 - H 3 ( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%) 0.0000 0.5774 0.0000 0.7071 0.0000 -0.4082 0.0000 0.0000 0.0000 ( 55.52%) 0.7451* H 3 s(100.00%) 1.0000 0.0000 3. (1.99853) BD ( 1) B 1 - H 4 ( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%) 0.0000 0.5774 0.0000 -0.7071 0.0000 -0.4082 0.0000 0.0000 0.0000 ( 55.52%) 0.7451* H 4 s(100.00%) 1.0000 0.0000 4. (1.99903) CR ( 1) B 1 s(100.00%) 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 5. (0.00000) LP*( 1) B 1 s(100.00%)

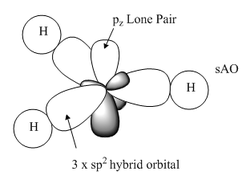
The hybridization of the molecule is clearly explained; each bond is described according to the contribution of boron and hydrogen together with the corresponding s and p character of their bonding orbitals. There are 3 hybrid sp² orbitals interacting with three hydrogen sAO's, a core 1sAO of boron and a lone pair which should be 100% p character but it has been calculated as 100% s character due to a lower accuracy basis set.

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis Threshold for printing: 0.50 kcal/mol E(2) E(j)-E(i) F(i,j) Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. ===================================================================== within unit 1 4. CR ( 1) B 1 / 10. RY*( 1) H 2 1.51 7.54 0.095 4. CR ( 1) B 1 / 11. RY*( 1) H 3 1.51 7.54 0.095 4. CR ( 1) B 1 / 12. RY*( 1) H 4 1.51 7.54 0.095

Natural Bond Orbitals (Summary): Principal Delocalizations NBO Occupancy Energy ============================================================ Molecular unit 1 (H3B) 1. BD ( 1) B 1 - H 2 1.99853 -0.43712 2. BD ( 1) B 1 - H 3 1.99853 -0.43712 3. BD ( 1) B 1 - H 4 1.99853 -0.43712 4. CR ( 1) B 1 1.99903 -6.64476 5. LP*( 1) B 1 0.00000 0.67666 6. RY*( 1) B 1 0.00000 0.37177 7. RY*( 2) B 1 0.00000 0.37177 8. RY*( 3) B 1 0.00000 -0.04532 9. RY*( 4) B 1 0.00000 0.43446 10. RY*( 1) H 2 0.00032 0.90016 11. RY*( 1) H 3 0.00032 0.90016 12. RY*( 1) H 4 0.00032 0.90016 13. BD*( 1) B 1 - H 2 0.00147 0.41201 14. BD*( 1) B 1 - H 3 0.00147 0.41201 15. BD*( 1) B 1 - H 4 0.00147 0.41201 ------------------------------- Total Lewis 7.99463 ( 99.9329%) Valence non-Lewis 0.00441 ( 0.0551%) Rydberg non-Lewis 0.00097 ( 0.0121%) ------------------------------- Total unit 1 8.00000 (100.0000%) Charge unit 1 0.00000

The first table predicts any possible mixing between molecular orbitals, however, it is only significant if its higher than 20 kcal mol^-1 which none are. The second summarises all the orbital occupancies and energies showing that all bonds are made up of two electrons as does the boron 1s non-bonding orbital.

---

---

Structural analysis of TlBr₃

---

Geometry Optimisation

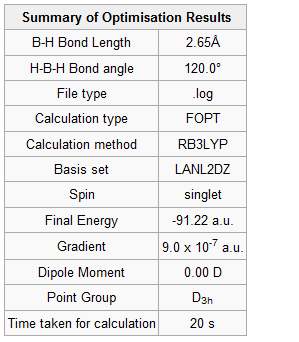
Both Thallium and Bromine atoms have many more electrons than relatively simple BH₃, this means calculating their electron density and energies would take too much time. As a result pseudo potentials are used to avoid solving the Schrodinger equation for the core electrons since they are not involved in bonding. Initially the molecule is constrained to a D_3h symmetry and then it is optimized with B3LYP and LANL2DZ; a medium accuracy basis set which employs Los Alamos ECP pseudo-potentials on heavier elements such as Thallium. DOI:10042/to-10973

Figure 6 Total energy and RMS gradient norm optimisation curves

Figure 7 Optimised geometries of the three iterations

Figure 6 and 7 show how the optimization occured, the molecule geometry underwent three iterations resulting in a very close to zero gradient at the third. As discussed for the previous example this stationary point could be a minimum or maximum and vibrational analysis is needed to prove which one it is.

---

Vibrational Analysis

To determine the vibrational modes of TlBr₃, DFT-B3LYP is still used as the method and LANL2DZ as the basis set just like in the optimisation above.

Figure 7 IR spectrum of TlBr₃

Summary of Frequency Results
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	LANL2DZ
Spin	singlet
Final Energy	-91.22 a.u.
Gradient	8.8 x 10-7 a.u.
Dipole Moment	0.00 D
Point Group	D3h
Time taken for calculation	21 s

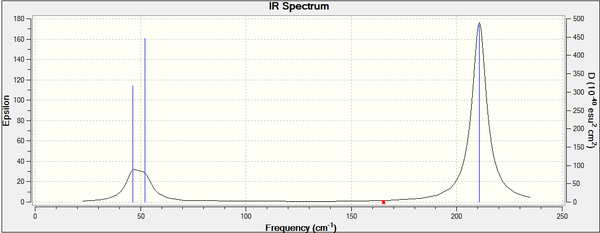
Values in the frequency calculation summary match those of the optimisation so it was completed successfully. The IR spectrum is similar to that of BH₃ with three peaks, two of which superimpose and broaden the overall peak, this is expected since both molecules have the D_3h point group. All vibrational modes are tabulated below and again their similarity to BH₃ is obvious, symmetric stretching is IR inactive and the two degenerate pairs are present too. The frequencies are lower in energy concurring with the longer bond lengths of 2.69Å (c.f. 1.93Å) and therefore weaker Tl-Br bonds .

Vibrational number	Frequency (cm-1)	Intensity	Vibrational mode	Symmetry D3h point group	Snapshot
1	46	3.7	Scissoring	E'
2	46	3.7	Rocking	E'
3	52	5.8	Wagging	A2
4	165	0.0	Symmetric Stretching	A'1
5	211	25.5	Asymmetric Stretching	E'
6	211	25.5	Asymmetric Stretching	E'

Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
Low frequencies ---   46.4289   46.4292   52.1449

The first line of low frequencies comes from the motion of the centre of mass and should be a lot lower than the "real" normal modes. In this case the largest "zero" frequency is close to 4 and the lowest "real" mode is 46.4 cm^-1, this is only a tenth but this low accuracy arises from the poor level of the method used. Nonetheless, all frequencies are positive confirming the minimum during optimisation.

A chemical bond is the sharing of electrons between two atoms leading to a molecule which is more stable than the individual atoms. A whole spectra of bond strengths exists depending on the stabilisation of the bonding orbital, this is proportional to the bond length. Gaussview has a predefined value for bond distance and when a bond is greater than this value it is not shown as for BH₃. Nonetheless a bond is better considered as localized electron density between two atoms thus the absence of a bond "line" makes no difference during MO/frequency calculations because electron density is taken into account.

---

---

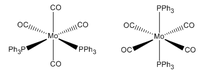
Cis and Trans Isomers of MO(CO)₄(PPh₃)₂

---

Geometry Optimisation

MO(CO)₄(PPh₃)₂ may have two triphenylphosphine groups in a cis or trans conformation. Since these complexes are too computationally demanding, the PPh₃ groups will be replaced by PCl₃ which are sterically just as large and contribute to bonding in a similar manner. Optimising the ground state structures begins by drawing the two complexes on gaussview and running an optimization with B3LYP and LANL2MB (minimal) basis set for each. Pseudo Potentials must be used again to model the core electrons and a loose convergence is established to get the rough geometry.DOI:10042/to-10976 and DOI:10042/to-10981

Summary of Optimisation Results
Isomer	Calculation type	Calculation method	Basis set	Spin	Final Energy (a.u.)	Gradient (a.u.)	Dipole Moment (D)	Point Group	Time taken for calculation	Structure
Cis	FOPT	RB3LYP	LANL2MB	Singlet	-617.5	1.9 x10-5	8.47	C1	19min 28s	Cis1

Trans	FOPT	RB3LYP	LANL2MB	singlet	-617.5	5.9 x10-5	0.00	C1	8min 10s	Trans1

Figure 8 Ideal orientation of PCl₃ groups in cis (left) and trans (right) isomers

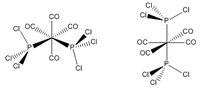
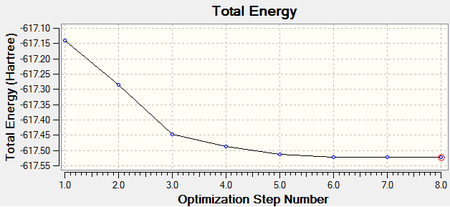
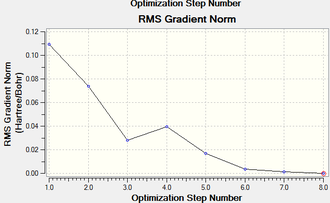
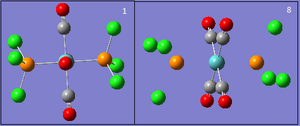
Both isomers reach the same final energy of -16.1 x 10⁶ kJ mol^-1. Cis has a dipole moment of 8.47D whereas Trans does not due to its high symmetry along the P-Mo-P plane. The energy curve shows 19 iterations for cis isomer, on the fourth an unstable geometry is isolated, however a stationary point is finally reached. For the trans isomer, optimization underwent only 8 iterations shown by a smooth curve and a resulting minimum. Since a low level method is used, unless the orientation of the PCl₃ groups is close to the ideal geometry, it will optimise until a zero gradient is obtained, however this could be a local minimum on the PES curve and a lower energy geometry might exist. The best orientation for PCl₃ in both isomers is shown in figure 8 and can be applied to the molecules in gaussview by altering torsional angles. For the cis conformer the Cl atoms in one group are rotated so that one points up parallel to the axial bond and on the other group the same is done but with a Cl pointing down. For the trans, PCl₃ are rotated until they eclipse and one Cl from each group lies on top of a C-O bond. After dihedral modification a more accurate optimization is carried out with a better pseudo-potential, basis set LANL2DZ and tighter convergence criteria. DOI:10042/to-10982 and DOI:10042/to-10986

Summary of Improved Optimisation Results
Isomer	Calculation type	Calculation method	Basis set	Spin	Final Energy (a.u.)	Gradient (a.u.)	Dipole Moment (D)	Point Group	Time taken for calculation	Structure
Cis	FOPT	RB3LYP	LANL2DZ	Singlet	-623.58	1.02 x10-5	1.31	C1	1hr 3min 49s	Cis2

Isomer	Calculation type	Calculation method	Basis set	Spin	Final Energy (a.u.)	Gradient (a.u.)	Dipole Moment (D)	Point Group	Time taken for calculation	Structure
Trans	FOPT	RB3LYP	LANL2DZ	singlet	-623.58	3.7 x10-5	0.31	C1	47min 38s	Trans2

The more accurate optimisation has resulted in a lower energy minimum for both isomers, a decrease of 15800 kJ mol^-1 and therefore a more stable geometry. Even the gradients are closer to zero confirming the tighter convergence of the calculation. Now it is time to verify the optimisation by analysing vibrational frequencies.

---

Vibrational Analysis

In this section I will analyze in more detail a) the structure, b) The relative energies and c) the vibrations of both the cis and trans isomers and relate this to their symmetry. Frequency calculation is carried out as shown below following the same parameters as the optimisation. A minimum is reached since final energy values stay constant. DOI:10042/to-10988 and DOI:10042/to-10989

Summary of Frequency Results
Isomer	Cis	Trans
Calculation type	FREQ	FREQ
Calculation method	RB3LYP	RB3LYP
Basis set	LANL2DZ	LANL2DZ
Final Energy (a.u.)	-623.577	-623.576
Gradient (a.u.)	1.03 x 10-5	3.73 x 10-5
Dipole Moment (D)	1.31	0.31
Point Group	C1	C1
Time taken for calculation	27min 13s	30min 37s

Structure

Geometric parameters of the isomers are tabulated below together with literature values to compare with. The cis isomer is compared with the bond lengths and angles determined from the crystal structure of the experimentally synthesised molecule. However, literature data for the trans isomer was not available so a similar structure with chromium replacing molybdenum was used to compare to the computed results. Cr and Mo are both in group 6, they have the same number of valence electrons and form analogous complexes.

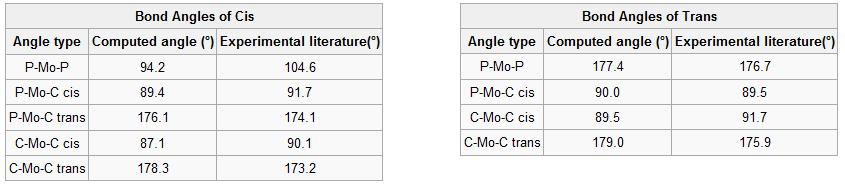
Bond lengths for Cis conformer are slightly different, they tend to be higher than reported values except for the Mo-P bond which is shorter, yet they are within a ±0.05Å error. Bond angles are similar too but P-Mo-P is 10° smaller because Cl atoms were used instead of phenyl groups thus leading to less steric strain between two cis PPh₃. For trans isomer the lengths are all longer with a greater error of ±0.1Å which is expected since chromium is the metal centre and being smaller than molybdenum it forms shorter Cr-P and Cr-C bonds. Nonetheless bond angles agree very well with literature. These geometric parameters confirm the structure and corresponding point groups of both complexes; C_2v and D_4h for the cis and trans forms respectively.

Relative Energies

There is a very small difference between the two isomers of 2.63 KJ mol^-1 and therefore no certain conclusion can be made on which isomer is more stable. This small preference for the cis isomer can be rationalized on the fact that two PPh₃ trans to each other will experience less steric repulsion, but the trans effect on cis stabilises this geometry.

Vibrations

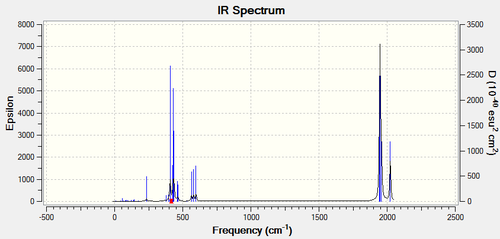
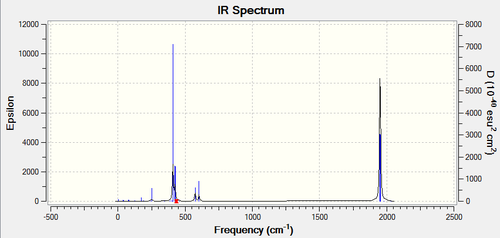
Both complexes have exactly 45 vibrational modes, most of them being IR inactive with low intensity. Looking at the IR spectra, the cis isomer has more peaks due to a lower symmetry and higher dipole moment of 1.31D. At very low frequencies below 20 cm^-1 two modes arise from the rotation of the Chlorine atoms away from their ideal orientation. These are low energy vibrations which are excited at room temperature and can be understood as oscillations at the minimum in the PES. All frequencies are positive thus a minima was reached during optimisation.

Cis Isomer				Trans Isomer
Figure 9 Infrared Spectrum of Cis isomer				Figure 10 Infrared Spectrum of Trans isomer
Mode number	Frequency (cm-1)	Intensity	Vibration	Mode number	Frequency(cm-1)	Intensity	Vibration
1	10.7	0.03		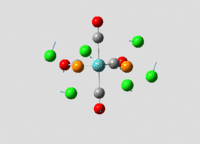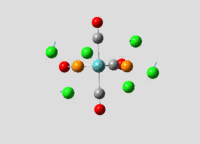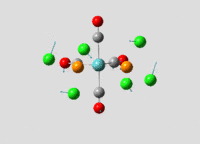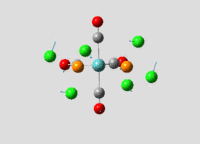1	4.9	0.09
2	17.6	0.01		2	6.1	0
C-O Vibrational modes
42	1945	763		42	1951	1475
43	1949	1499		43	1951	1467
44	1958	633		44	1977	0.64
45	2023	598		45	2031	3.77

The vibrational modes of the carbonyl stretches can help us verify the geometry of the molecule. For the cis isomer, the 4 C-O vibrations are IR active as they show high intensities in the spectrum, whereas for the trans isomer two are degenerate and yield a single peak and the other two are inactive with very low intensities. Since IR inactive vibrations force no change in the dipole moment of the molecule the symmetry has to be higher for the trans complex. Using the character table for the two point groups these modes can be assigned to a specific symmetry.

Molecular symmetry	Cis (C2v)				Trans (D4h)
Vibration Frequency cm-1	1945	1949	1958	2023	1951	1951	1977	2031
Literature Frequency cm-1	1941	1948	1965	2049	1943	1943	1985	2050
Stretch vectors
Stretch type	asymmetric cis	asymmetric trans	symmetric cis and trans (out of phase)	All symmetric	Asymmetric trans	Asymmetric Trans	Both symmetric (out of phase)	All symmetric
Vibration symmetry	B2	B1	A1	A1	Eu	Eu	B1g	A1g

Computed frequencies relate very well to the reported values even though P(OC₆H₅)₃ is used instead of triphenyl phosphine.

---

---

Miniproject: Sulphur Tetrafluoride

SF₄, the simplest known sulfurane, is a gas at room temperature and is used as a flourinating agent in the synthesis of organofluorine compounds. Sulphur is present in the +4 oxidation state with two electrons forming a lone pair. Having 10 electrons overall in its valence shell makes it hypervalent and therefore an interesting molecule to analyse both structurally and electronically.

---

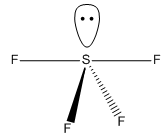
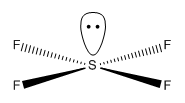
Geometry

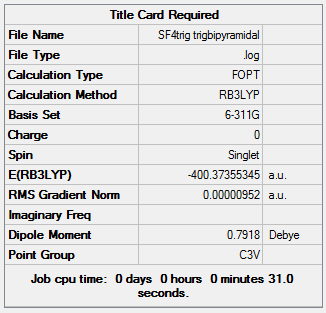
Its geometry is essentially described as trigonal bipyramidal with a lone pair occupying one of the equatorial sites. VSEPR theory predicts it to be pseudo see-saw shaped since the lone pair pushes the two equatorial and two axial fluorine atoms away reducing all F-S-F bond angles. Even though it is less likely that the lone pair occupies the axial position it is worth considering it as a possible structure. Lastly, it is known that SF₄ is isoelectronic with ClF₄⁺ so another option would be square pyramidal with the lone pair occupying the axial site. All these geometries can be optimized computationally using DFT-B3LYP as the method and a high accuracy 6-311G basis set. By not constraining the molecules to a specific point group the lowest energy configurations for all 3 geometries can be obtained, these are tabulated below: DOI:10042/to-10990 , DOI:10042/to-10991 and DOI:10042/to-10992

See-Saw	Trigonal bipyramidal	Square pyramidal

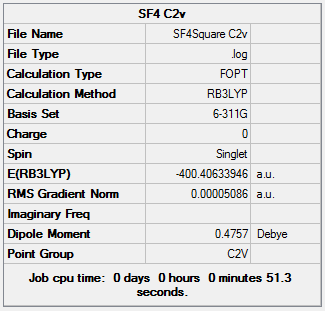
The see-saw geometry is by far the most stable having an energy 1.04 x 10⁶ kJ mol^-1 lower than the other two and nearly twice as stable. This is expected since the lone pair destabilises trigonal and square pyramidal by repelling fluorine atoms away from the equatorial plane. The geometric parameters below prove the discussion above, for example bond angle F_ax-S-F_eq in trigonal bipyramidal structure is 83° instead of being 90°.

S-F axial	1.82Å	S-F axial	1.36Å	S-F	1.46Å
S-F equatorial	1.75Å	S-F equatorial	1.70Å
F-S-F axial	165.9°	Fax-S-Feq	83.0°	F-S-F trans	162.8°
F-S-F equatorial	107.2°	F-S-F equatorial	119.3°	F-S-F cis	88.7°

Values for the see-saw geometry can be compared with literature, S-F axial and equatorial bonds are reported to be 1.73Å and 1.64Å respectively suggesting that the computed bond lengths are about 0.1Å higher, yet axial and equatorial lengths are different. The bond angles are quite similar with axial being 173° and equatorial 102°, again the basis set has overestimated the size of bond angles because it probably doesn't take into account how the lone pair affects the electron density around the molecule.

---

Vibrational analysis

By calculating the vibrational modes and the IR spectrum of SF₄ one can confirm to which point group the molecule belongs to. If the see-saw geometry (C_2v symmetry) is used for the calculation then the modes are given themselves a symmetry belonging to that particular point group. A mode which doesn't alter the dipole moment of the molecule has zero intensity in the spectrum, thus a comparison of the experimental spectrum with the computed one can confirm which geometry it has. Frequency calculation is carried out with identical method and basis set as the optimisation (B3LYP and 6-311G) and specifying a full population analysis. DOI:10042/to-10993

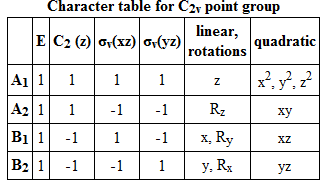
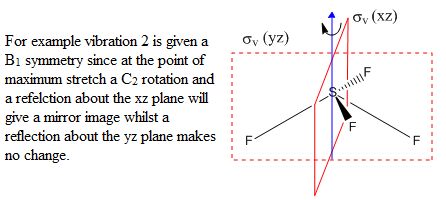
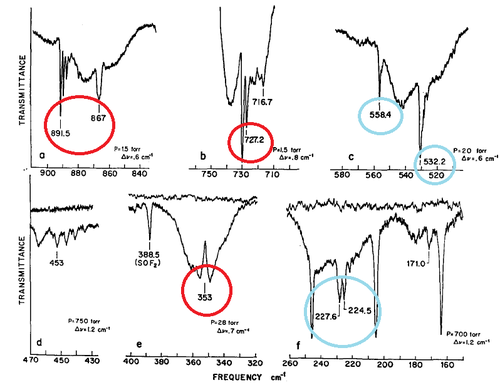
Vibrational number	Frequency (cm-1)	Intensity	Literature frequency (cm-1)	Vibrational mode	Form of vibration	Symmetry C2v point group
1	97	0.87	228	axial deformation		A1
2	254	16.64	353	axial deformation		B1
3	327	0.00	414	twist		A2
4	351	30.39	475	SF2eq deformation		A1
5	361	4.34	532	FSF2eq deformation		B2
6	498	2.11	558	Symmetric S-F stretch (axial fluorines)		A1
7	683	49.16	730	Symmetric S-F stretch (equatorial fluorines)		A1
8	697	98.94	867	Asymmetric S-F stretch (equatorial fluorines)		B1
9	737	323.43	892	Asymmetric S-F stretch (axial fluorines)		B2

The spectrum on the left is taken from the same paper as the reference values. Comparing computed frequencies with the literature shows that they are all lower than expected by approximately 100cm^-1. This systematic error may arise from insufficient accuracy of the calculation. Out of the nine vibrations only five come up in the spectrum on the right, the remaining four have intensities below 5 and are thus IR inactive. I have highlighted in red the peaks which show up in both spectra, these are vibrations 2,7,8 and 9. Vibration 4 should also be present in the reported spectrum at 475cm^-1. The peaks highlighted in blue are the ones which are IR inactive and are dubbed as weak.

Low frequencies ---  -21.6902   -0.0034   -0.0006    0.0019   14.1694   31.3250
Low frequencies ---   96.5510  254.2327  326.9733

An explanation for why the frequencies are off the reported values could be because the highest "zero" frequency of -22 cm^-1, originating from the motion of the center of mass, is very high relative to the lowest vibration of 97 cm^-1. All frequencies are positive so the minimization has converged to a minimum.

---

Molecular Orbital analysis

A molecular orbital diagram of sulfur tetrafluoride can be computationally prepared by calculating the energies of the molecular orbitals. Even graphic representations of these orbitals can be made and then compared with the LCAO'S. To work out the qualitative MO's the SF₄ molecule is split up into two fragments; SF₂ and F-·-F which represents the axial fluorine atoms. Bringing the orbitals of the same symmetry together can produce good approximates of the graphical MO's as done in this journal. The energy calculation is run with B3LYP and 6-311G basis set together with pop="full" and full NBO.DOI:10042/to-10994

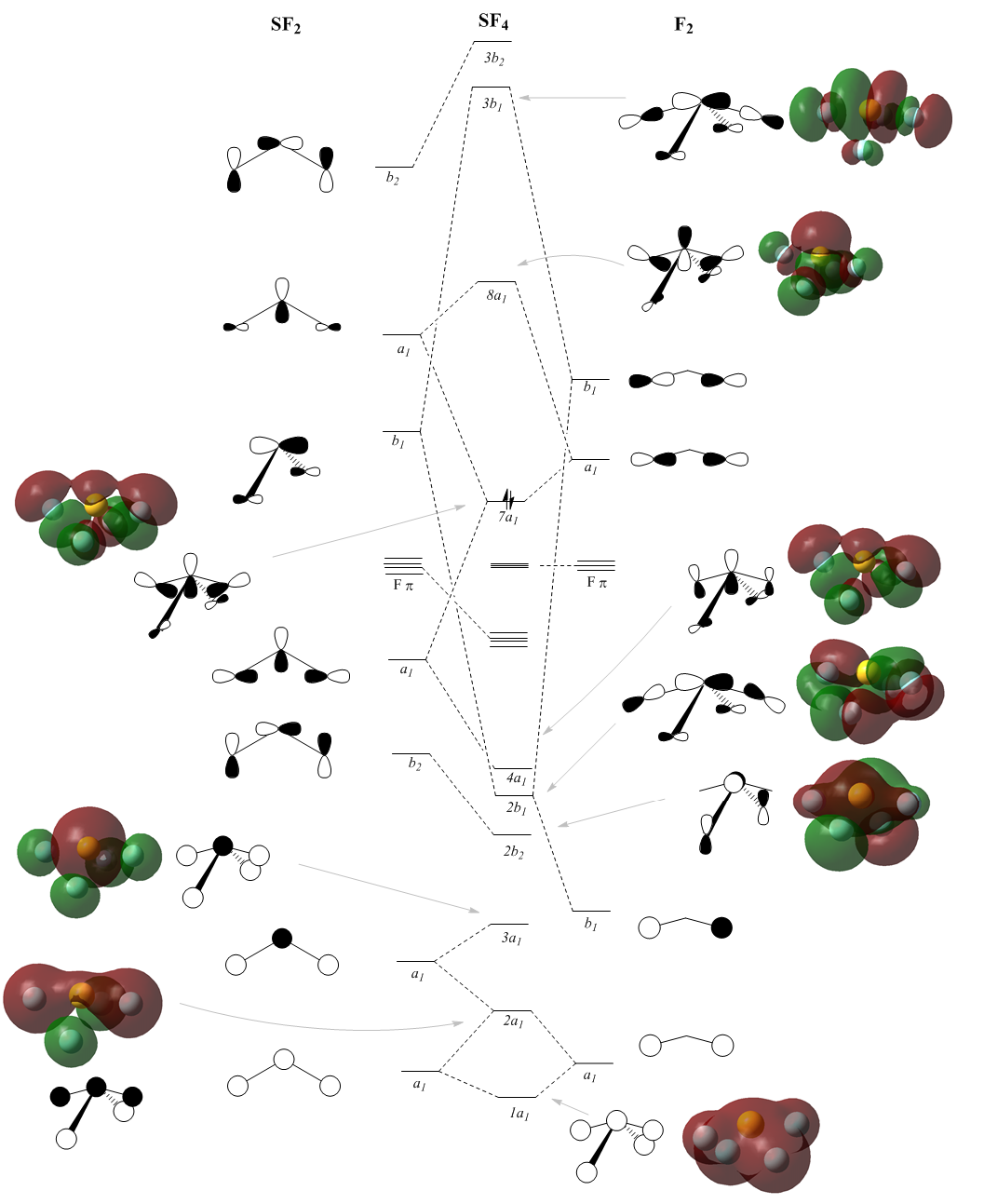
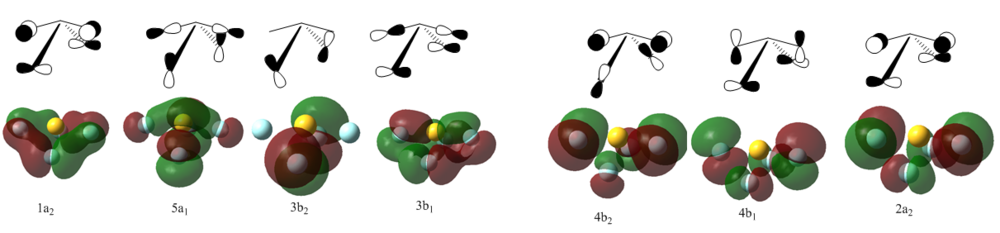
The calculation resulted in a total of 73 orbitals, most of them anti bonding and insignificant since the HOMO is the 26th. Out of the bonding orbitals the lowest energy ones are the s, p_x, p_y and p_z of the sulphur atom only, these range from -8.3 to -6.2. Then between -1.30 to -1.18 there are four orbitals: one with all atoms in full s character, two with S p and F s and the fourth with all s but axial antibonding. Consequently the fluorine atoms also adopt p character and explaining the MO's becomes very difficult. The diagram is a simplification as it excludes many of the confusing orbitals. For example Fπ orbitals whereby sulphur is non-bonding but fluorine atoms bond with their p orbitals are not included. The Fπ molecular orbitals are shown below. The HOMO (7a₁) agrees very well with the literature as do other computed MO's.

---

NBO analysis

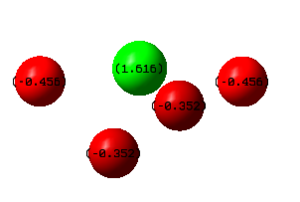
Running the energy calculation for MO analysis also gives us information on the natural bond orbitals of SF₄. The table below taken directly from the .log file shows how all of the positive charge is concentrated on the Sulphur atom. Negative charge is distributed unevenly between axial and equatorial fluorines, the former having a greater negative charge, which makes sense as S-F axial bond lengths are longer.

Summary of Natural Population Analysis: Natural Population Natural ----------------------------------------------- Atom No Charge Core Valence Rydberg Total ----------------------------------------------------------------------- S 1 1.61567 9.99995 4.35450 0.02989 14.38433 F 2 -0.45567 1.99999 7.45346 0.00222 9.45567 F 3 -0.35216 1.99999 7.34984 0.00233 9.35216 F 4 -0.45567 1.99999 7.45346 0.00222 9.45567 F 5 -0.35216 1.99999 7.34984 0.00233 9.35216

(Occupancy) Bond orbital/ Coefficients/ Hybrids --------------------------------------------------------------------------------- 1. (1.82959) BD ( 1) S 1 - F 2 ( 17.53%) 0.4186* S 1 s( 18.31%)p 4.46( 81.69%) 0.0000 0.0000 -0.1506 0.4003 -0.0105 -0.0006 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.7062 0.0362 0.0066 -0.0012 0.0000 0.2968 0.4750 0.0559 0.0120 ( 82.47%) 0.9082* F 2 s( 4.90%)p19.40( 95.10%) 0.0000 -0.2213 -0.0059 0.0005 0.0000 0.0000 0.0000 0.9738 0.0021 -0.0012 -0.0510 -0.0005 0.0005 2. (1.91229) BD ( 1) S 1 - F 3 ( 28.04%) 0.5296* S 1 s( 8.73%)p10.45( 91.27%) 0.0000 0.0000 0.2410 0.1709 -0.0062 -0.0004 0.0000 -0.7061 0.0378 0.0021 0.0013 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.5738 0.2870 0.0307 0.0080 ( 71.96%) 0.8483* F 3 s( 5.01%)p18.95( 94.99%) 0.0000 0.2239 -0.0002 -0.0006 0.7938 0.0006 -0.0010 0.0000 0.0000 0.0000 0.5655 0.0008 -0.0010 3. (1.82959) BD ( 1) S 1 - F 4 ( 17.53%) 0.4186* S 1 s( 18.31%)p 4.46( 81.69%) 0.0000 0.0000 0.1506 -0.4003 0.0105 0.0006 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.7062 0.0362 0.0066 -0.0012 0.0000 -0.2968 -0.4750 -0.0559 -0.0120 ( 82.47%) 0.9082* F 4 s( 4.90%)p19.40( 95.10%) 0.0000 0.2213 0.0059 -0.0005 0.0000 0.0000 0.0000 0.9738 0.0021 -0.0012 0.0510 0.0005 -0.0005 4. (1.91229) BD ( 1) S 1 - F 5 ( 28.04%) 0.5296* S 1 s( 8.73%)p10.45( 91.27%) 0.0000 0.0000 -0.2410 -0.1709 0.0062 0.0004 0.0000 -0.7061 0.0378 0.0021 0.0013 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.5738 -0.2870 -0.0307 -0.0080 ( 71.96%) 0.8483* F 5 s( 5.01%)p18.95( 94.99%) 0.0000 -0.2239 0.0002 0.0006 0.7938 0.0006 -0.0010 0.0000 0.0000 0.0000 -0.5655 -0.0008 0.0010 14. (1.99866) LP ( 1) S 1 s( 83.78%)p 0.19( 16.22%) 0.0000 0.0000 0.9152 0.0157 -0.0001 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.4020 0.0260 -0.0023

The axial S-F bonds seem to have less electron density that equatorial S-F bonds whereas the lone pair holds 2 electrons precisely. Fluorine atoms are highly electron withdrawing so that almost 75% of electron density is pulled towards them. The hybridization of the sulfur is hard to determine yet a qualitative way to approach it is to assume that see-saw geometry mimics trigonal bipyramidal and therefore sulfur is sp³d hybridized. However, it is important to avoid sulfur 3d orbital participation and better model would be a 3c-4e^- description of the axial F-S-F bond.

---

---