Rep:Mod:mpg15MgOreport

Marcin Giza MgO Report

Introduction

MgO forms a simple face centred cubic crystalline structure in its solid form. The properties and behaviour of this structure can be investigated with the use of computer simulations. In the case of this experiment, the software in use was DLVisualize, which ran GULP (General Utility Lattice Program) to perform the calculations necessary.

The experiment focused on the use of two different theoretical models of simulating the behaviour of atoms in a crystal - the quasi-harmonic approximation, and molecular dynamics. They are based on two fundamentally different approaches to the problem. The quasi-harmonic approximation is a quantum model of atomic bonding, treating all atoms within the crystal as simple harmonic oscillators. This idea is applied to a theoretical infinite crystal lattice, which has the effect of reducing the motion of atoms within the crystal to a series of discrete vibrations across the lattice. These modes of motion are phonons, and the study of phonons and their distribution allows us to determine the physical properties of the crystal lattice. The 'quasi' element of the quasi-harmonic approximation comes from a small adjustment to the simple harmonic model. The phonon frequencies are treated as being dependent on the volume of the cell. This allows us to extract thermodynamic data such as the thermal expansion coefficient, which would be impossible if the harmonic approximation was used. The second model in use is molecular dynamics. This is a Newtonian model of atomic bonding, which looks at the forces acting on a number of atoms within a finite cell. A simulation is performed by calculating the motion of atoms at incremental time steps, while constantly calculating the sum of the forces acting on each atom. Thermodynamic properties are determined by allowing the system to reach an equilibrium over a sufficient period of time.

The two models above were applied to determine the dependence of the cell volume and free energy on temperature, and to calculate the thermal expansion coefficient of MgO.

Results and Discussion

Part 1: Phonon DOS

The initial investigation focused on the use of the quasi-harmonic approximation to find the dependence of the Density of States of the system on the shrinking factor chosen for the system. The density of states is a mapping of the phonon frequencies of the system, showing which ones are dominant in the molecule.

11 different calculations were ran, using the following shrinking factors: 1,2,3,4,5,6,8,16,24,32 and 40.

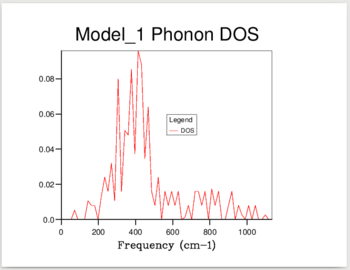
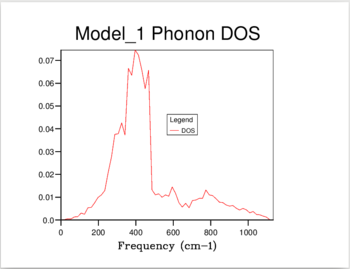
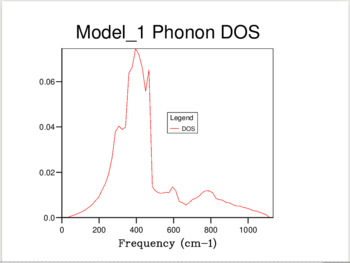
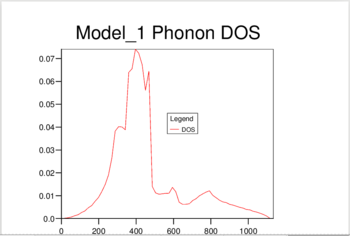
The increase in shrinking factor meant more k-points were sampled, giving a higher resolution for the calculated DoS. For the 1,1,1 shrinking factor, there was only one k-point sampled, at 0.5,0.5,0.5 - the center of the inverse space, which resulted in a DOS with only 4 peaks. When a shrinking factor of 40 was used, there were 32,000 point samples, and the DOS was a smooth continuum. The DOS showed essentially no change past a shrinking factor of 24, which was chosen as the optimum value to minimize calculation time.

Figure 1: DOS Calculations

Shrinking Factor 5	Shrinking Factor 16	Shrinking Factor 24	Shrinking Factor 40

As shown in Figure 1, at a shrinking factor of 24 we get a smooth DOS curve, without any of the jagged behavior which is visible in all previous shrinking factors. The DOS reflects the nature of the the Phonon dispersion curve for MgO. As it is formed by sampling the k-space at different intervals, a picture is built up of the number of vibrations present at each value of k. The curve of the density of states will then give us information about which regions in the Phonon dispersion curve have low gradients, and therefore many different k points with vibrations at that frequency. The large peak at 300-500 cm^-1 reflects the large horizontal band in the curve. (Figure 2)

Figure 2: Phonon Dispersion Curve

Part 2: Free Energies

To confirm the choice of a shrinking factor of 24 as the optimal one, energy calculations for the system were performed using the quasi-harmonic model. The range of shrinking factors investigated was the same as previously.

Figure 3: Energy Calculations

Free Energies 1	Free Energies 2	Zero Point Energies

As visible in Figure 3 above, the free energies converged to a single value of -40.926483eV at a shrinking factor of 24, confirming it as the optimal point to carry out any further simulations. At the two lowest shrinking factors, the system showed erratic behavior, overestimating the free energy. Only from a shrinking factor of 3 did a normal behavior begin. The free energy value at this point is only 0.051meV from the equilibrium, showing a relatively high accuracy can be achieved with a very small shrinking factor.

The zero point energy converged to a single value much faster, steadying at 0.174340eV at a shrinking factor of 5.

The optimal shrinking factor of 24 is not a universally appropriate value, and will change depending on the system being investigated. The accuracy of the simulation depends on the number of phonon modes sampled, which depends on both the shrinking factor used and the size of the k-space. Since the k-space is inversely proportional to the size of the lattice, a larger lattice will have a smaller k-space, and so a smaller number of points will need to be sampled along it to extract a reasonable amount of information for an accurate simulation. To try to judge whether the shrinking factor will need to be larger or smaller, the lattice parameters of the crystals must be compared. The lattice parameters of the systems of interest are as follows: Lithium: 3.49Å; Faujasite: 24.7Å; Calcium Oxide: 4.81Å; Magnesium Oxide: 4.21Å;

The two oxides are relatively close together in size, and thus their k-spaces will be of a similar size, and thus the shrinking factor of 24 should remain appropriate. Faujisite has a much larger lattice parameter, and thus we can expect a much smaller shrinking parameter to be adequate. The opposite is the case with lithium. Since it has a smaller lattice, the shrinking factor would need to be larger. The difference is not too significant however, so the increase of shrinking factor should not be large.

Part 3: Thermal Expansion

Figure 4: Thermal Expansion Properties

Free Energies	Lattice Parameters

Figure 4 shows two plots of free energy and lattice parameter vs temperature. Calculations were performed at temperatures in the range of 0-1500K, in 100K intervals. To perform the fit to the data the first three data points were ignored, as they did not follow the linear behaviour seen at higher temperatures. This is due to the quasi-harmonic approximation used, which includes a zero-point energy, which will have a considerable contribution at low temperatures. Calculations at temperatures approaching the melting point of MgO could not be completed, due to the excessive computational time they required.

Figure 4 also shows evidence that a linear fit is not appropriate when dealing with both the energies and the lattice parameters of the system. Both graphs show a clear deviation from linear behaviour, with datapoints curving away from the fitted line, especially at higher temperatures. In the case of the thermal expansion, an assumption was made that the coefficient of thermal expansion is independent of temperature. The shape of the graph is evidence that this is not the case, showing that the coefficient increases as temperature goes up. In the case of the free energy, the curve of the graph shows a dependence of the heat capacity of the MgO crystal on the temperature of the system.

The coefficient of the volume thermal expansion was calculated using the equation:${\alpha }_V=\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_p$

The value taken for V was the lowest values used in the fit, which was the first to match closely to the expected linear behaviour. The gradient of the linear fit calculated in python was used for the ${\left(\frac{\partial V}{\partial T}\right)}_p$ term.

α_V Value Comparison

Calculated αV	3.1176x10-5
Literature Values	T=300K	T=500K	T=1000K
Measured αV	3.12x10-5	3.84x10-5	4.46x10-5
Calculated αV	2.88x10-5	4.02x10-5	5.03 x10-5

A comparison of the calculated value of α with values taken from the literature for a range of temperatures similar to those used in the experiment shows a relative similarity. The calculated value is closest to those reported at 300K, almost exactly matching the measured value. The true accuracy of the calculated result is questionable however, as it is evident from the datapoints that a linear approximation is not appropriate in this situation. At temperatures of 1000K, the difference between the calculated and literature values is 38%, which, whilst significant, is still within the same order of magnitude and so suggests that the calculated value is not completely incorrect.

The thermal expansion this coefficient describes is caused by the increase in kinetic energy, which increases the vibrational motion of the atoms within the crystal, leading to a greater average separation and thus an expansion of the unit cell and an increase in the volume of the crystal. This is similar to the behaviour expected from a diatomic molecule following a harmonic potential, which will display an increase in bond length with increasing temperature due to the increasing magnitude of its vibrational motion. As the temperatures continue to rise, there will be an increase in the discrepancy between the phonon mode representation of the motion of the ions and the actual situation. The quasi-harmonic potential used to model the modes will simply predict a continually increasing vibration intensity, when in fact at temperatures near the melting point, the bonding in the MgO crystal will begin to break down and a phase transition will occur.

Part 4: Molecular Dynamics

Figure 5: Comparison of Molecular Dynamics and Quasi-Harmonic approximation.

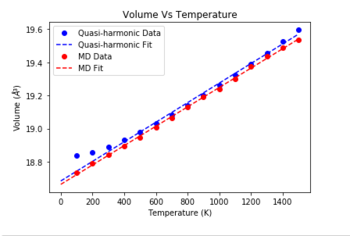
Figure 5 shows the difference between the Molecular Dynamics calculation and the Quasi-Harmonic model. To adjust the result of the molecular dynamics calculation, which gave the volume of the 32 atom cell, the output volumes were divided by 18 to make them match the primitive cell volumes calculated by the quasi-harmonic model. Once this was performed, a comparison between the two modes of simulation could be made. The most obvious difference is the lack of a non-linear section at low temperatures. This is due to the fact the Molecular Dynamics method uses a purely newtonian model of interatomic interactions to simulate vibrations, so no quantum behaviour is seen. Certain molecular dynamics methods include corrections to account for quantum behaviour at low temperatures, but the almost perfectly linear spread of datapoints suggests that the model used by GULP to perform the calculations lacks these corrections. A closer analysis of the datapoints themselves shows that the two models are in closest agreement at around 800K, where the primitive cell volume predicted by both modes of calculation is almost the same. At temperatures above this, the quasi-harmonic model begins to overestimate the increase in volume of the cell. This can be attributed to the fact the model neglects higher-order anharmonic terms, which have an increasingly significant contribution with rising temperatures. This suggests that the region of 800K is temperature where there is no significant contribution from quantum or anharmonic behaviour, suggesting that the crystal vibrates in a relatively 'uniform' manner that follows both newtonian and harmonic models of motion. At higher temperatures, it can be expected that the Molecular Dynamics simulation will start to show much larger fluctuations and a steeper increase in crystal volume, as the motion of the particles begins to approach that of a liquid. This behaviour is unlikely to be seen form the quasi-harmonic model, which will underestimate the anharmonic behaviour which will lead to melting of the crystal. The cell size used in the molecular dynamics calculation should be appropriate following the reasoning used for the quasi-harmonic approximation. Since the MgO crystal was made up of 32 unit cells, it can essentially be viewed as a cell with a lattice parameter 3.17 times larger than the single MgO cell. Since the lattice parameter is much larger, a single sampling point will be likely to give us sufficient information about the behaviour of the system to be able to make reasonably accurate predictions.

Conclusion

Multiple simulations were ran in DLVisualise software to investigate the properties of the MgO crystal. A quasi-harmonic approximation was utilised for the first stage of the experiment. A shrinking factor of 24 was determined to be the optimum one to be used in further simulations. These were used to plot a number of different properties of the crystal, such as the dependence of the lattice parameter and free energy on volume. This data was used to determine the volume expansion coefficient. It was calculated to be 3.1176x10^-5, which was a reasonable match to the literature values. Molecular dynamics simulations were then ran to compare the results with those obtained with the quasi-harmonic approximation. The two methods showed increasing deviation at high and low temperatures, with a very close match at around 800K.