Rep:Mod:mp1614TS

Transition states

Introduction

The potential energy surface (PES) is a mathematical function that describes the energy of a molecule in terms of the position of its atoms. The first derivative of energy with respect to position is the gradient, and when points have a gradient of zero, they have a physical meaning and are named stationary points. Energy minima correspond to stable species such as reactants, products or intermediates. Energy maxima correspond to the transition state, a state through which reactants must pass through to form products. The second derivative of energy with respect to position gives the curvature, and allows for a minima and transition state to be differentiated, as a energy minima has a positive second derivative while a transition state has a negative second derivative. A frequency calculation can be used to determine whether there is a structure at either of the points as there should only be one imaginary vibrational frequency, corresponding to the formation of the transition state. This arises from the fact that the curvature is negative, and when used in the equation to calculate the wavenumber, $\tilde{\nu }$, gives a negative frequency.

The objective of this computational laboratory was to study the reaction pathways of various Diels-Alder reactions involving different reactants and their transition states using the energy surfaces for the reactions. Diels-Alder reactions are [4+2] cycloadditions between a conjugated diene and a dienophile to form a substituted cyclohexene. The reaction is driven by the formation of 2 new σ-bonds, which are more stable than the π-bonds.

The transition states of these reactions were modelled using Gaussian and various optimisation methods in order to complete the exercises. Each of the optimisation methods has the main problem of solving a differential equation for a particle with respect to either its position for (classical) or its wave function(quantum). In the latter case, the differential equation being solved is the non-relativistic Schrödinger equation with the addition of relativistic corrections, and it is solved by creating a hamiltonian matrix for the system, and then solving the integrals. The first method used was the PM6 method, a semi-empirical method in which some of the integrals have values that are pre-determined, allowing for the calculation to take less time to run, but a cost to the the accuracy of the result given by the calculation. The second method involved using Density Functional Theory (DFT) at the B3LYP/6-31G(d) level. DFT involves using electron density to obtain the ground state properties of a system. Unlike the PM6 method, no integrals have pre-determined values, and all integrals must be solved. This leads to a longer time needed to run the calculation, but has the benefit of providing a more accurate result.

Nf710 (talk) 14:30, 10 February 2017 (UTC) your undertsanding of a TS is almpst cprect but not quite. Its not interm sof postions it is in terms of the normal modes (degrees of freedom of a molecules) a TS has one of the demensions second derivatives as a negative

Exercise 1: Reaction of Butadiene with Ethylene

In this exercise, the reaction between Butadiene and Ethylene was studied at the PM6 level. This reaction is a [4+2] cycloaddition in which butadiene acts the diene, and ethylene acts as the dienophile to form cyclohexene as the final product. This reaction is a Diels-Alder reaction in which the HOMO of butadiene reacts with the LUMO of the ethylene, making this a normal electron demand Diels-Alder reaction. This can be explained by consideration of the reactant's frontier molecular orbitals. The figure below shows the reaction scheme.

Reaction scheme

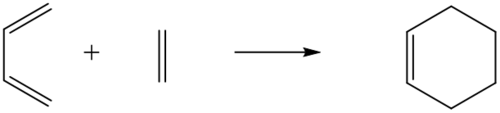Molecular Orbitals

By considering the frontier orbitals of butadiene and ethylene, we can class the type of reaction occurring as well as identify the necessary requirements for the formation of a MO from fragment orbitals. If a molecule has a centre of symmetry, the orbitals can be assigned a symmetry label depending on their behaviour on inversion through the centre. If inversion results in the same phase for the molecular orbital, the orbital has gerade (g) symmetry. If inversion through the centre of symmetry results in a phase change, the orbital has ungerade (u) symmetry. The MO diagram below shows the key orbitals that interact in this particular reaction to give the cyclohexene transition state, along with their symmetry labels.

MO diagram of the Cyclohexene transition state

From the diagram, we can see that 2 orbitals of butadiene and 2 on ethylene combine to yield 4 new molecular orbitals in the cyclohexene transition state. We can see that the HOMO of butadiene interacts with the LUMO of ethylene, while the LUMO of butadiene interacts with the HOMO of ethylene.

Nf710 (talk) 14:32, 10 February 2017 (UTC) These symetry labels are wrong. You have used u and g when this means there is a center of inversion.

Ethylene MOs	Butadiene MOs	Transition state MO
HOMO	HOMO	HOMO	LUMO
LUMO	LUMO	HOMO-1	LUMO+1

The MOs calculated above match up to the MO diagram showing that the HOMO of butadiene interacts with the LUMO of ethylene as they are both have ungerade symmetry, and the HOMO of butadiene interacts with the LUMO of ethylene as they are both have gerade symmetry. By considering the MOs formed from the fragment orbitals on butadiene and ethylene, it can be seen that only fragment orbitals with the same symmetry label of g or u can form an MO. This is a consequence of the quantum mechanical nature of the symmetry interactions of the wavefunctions for the considered orbitals. The overlap of two atomic orbitals can be quantified using the overlap integral, which is defined as

$S_{AB}=\int {\psi }_A^{*}{\psi }_{B}dV$

where A and B are 2 arbitrary atoms, and the integral is over all space.

The result given by this integral is the key to determining whether a reaction is allowed or forbidden, and specifically whether the integral is zero or non-zero. Overlap between orbitals of the same symmetry (such as gerade-gerade or ungerade-ungerade) leads to a non-zero integral being obtained, corresponding to an allowed reaction. Overlap between orbitals of opposite symmetry (such as ungerade-gerade or gerade-ungerade) leads to an integral of zero being obtained, corresponding to a forbidden reaction. This accounts for the fact that in this reaction, only the HOMO on 1 molecule can interact with the LUMO of the other molecule, and that there is no observed HOMO-HOMO or LUMO-LUMO interactions.

Measurement of bond lengths

Mechanism of the [4+2] cycloaddition of butadiene and ethylene

The figure above shows the concerted nature of the Diels-Alder reaction between butadiene and ethylene. By using computational calculations, we are able to explore the bonds lengths of the transition state, something that is not possible in a real life experiment due to the extremely short lifetime of the transition state. Experimentally measured values of C(sp³)-C(sp³), C(sp²)-C(sp²) and C(sp³)-C(sp²) are 1.54 Å, 1.33 Å and 1.50 Å.

Bond	Bond Length (Å)
	Reactants	Transition State	Product
C1-C2	1.33532	1.38307	1.50990
C2-C3	1.46838	1.40721	1.33706
C3-C4	1.33532	1.38307	1.50990
C4-C5	-	2.27216	1.53739
C5-C6	1.325916	1.38607	1.53482
C6-C1	-	2.27215	1.53738

The table above shows the calculated bond lengths for this all the species in this Diels-Alder reaction. In the butadiene molecule, carbon-carbon double bonds were approximately 1.33 Å, while the carbon-carbon single bonds were around 1.47 Å. The single carbon-carbon bond in ethylene has a length of 1.32 Å. In the transition state, bond lengths in-between a single and double carbon bond were calculated. The two new carbon-carbon bonds that are forming between the ethylene and butadiene molecules were calculated out to be 2.28 Å. In the cyclohexene product, the single carbon-carbon bond lengths were found to be 1.54 Å while the double bond was found to be 1.34 Å.

Comparison of these calculated lengths to the experimentally measured lengths shows both values are in good agreement. This highlights the accuracy of computational methods in modelling the structures of molecules. The Van der Waals radii of carbon is 1.70 Å , and comparison with the bond lengths for the 2 new sigma bonds forming in the transition state (2.27 Å for C1-C6 and C5-C4) shows the concerted nature of the reaction.

Vibrations

Reaction path at the transition state

The vibration animated above shows that the formation of the two bonds is in a synchronous manner. This can be highlighted by the lengthening of the double bonds in butadiene and ethylene as they become single bonds, along with the simultaneous shortening of the single bond in butadiene as is becomes a single bond. We can also see how the geometry of the carbon centers 1,4,5 and 6 distort from a trigonal planar shape to a tetrahedral shape as the reaction progresses.

Nf710 (talk) 14:54, 10 February 2017 (UTC) Good first section, the symmetry labels are wrong. What is the electron demand of this reaction?

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

In this reaction, cyclohexadiene and 1,3-dioxole also undergo a [4+2] cycloaddition, in which cyclohexadiene acts the diene, and 1,3-dioxole acts as the dienophile. All calculations were done at the PM6 level first and then reoptimised at the B3LYP/6-31G(d) level. While this is also a Diels-Alder reaction similar to that in exercise 1, it is markedly different due to the fact that there are 2 possible products with different stereochemistry. These are named the exo and endo products, and arise from the fact that a substituent on the dienophile can affect the transition state of a reaction. In this case, the 2 O atoms bound to the double bond in the dienophile act as electron donating groups, and can not only affect the relative energies of the fragment orbitals, but can also affect the stereochemistry of the transition state and product due to secondary orbital interactions. The possibilty of 2 different products is highlighted in the reaction scheme below.

Reaction scheme

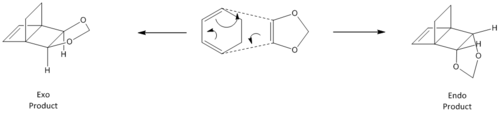Molecular Orbitals

The MO diagram below shows the key orbitals that interact in this [4+2] cycloaddition to give the transition state of the reaction between cyclohexadiene and 1,3-dioxole.

MO diagram of the reaction transition state

(These are not the correct symmetry labels! We specifically state to use symmetric/antisymmetric Tam10 (talk) 12:06, 8 February 2017 (UTC))

From the diagram, we can see that the fragment orbitals of cyclohexadiene and 1,3-dioxole interact similarly to the orbitals of butadiene and ethylene, in the sense that 2 orbitals on both the diene and dienophile combine to yield 4 new molecular orbitals in the transition state. However, unlike the previous reaction, we can see that the interaction between the LUMO of the diene and HOMO of the dienophile is the strongest interaction.

Transition state	MO
	HOMO-1	HOMO	LUMO	LUMO+1
Exo	HOMO-1	HOMO	LUMO	LUMO+1
Endo	HOMO-1	HOMO	LUMO	LUMO+1

The calculated MOs above show the nature of secondary orbital interactions in the endo transition state, with the orbitals on both oxygen atoms only being to interact with the pi orbitals in the cyclohexadiene molecule in this endo transition state. The MOs for the exo transition state illustrate how there can be no/little possible interaction between the orbitals on oxygen and the cyclohexadiene pi system due to the relative orientation of the two molecules. Eventhough the exo-product is the more thermodynamically stable due to less steric clash between the 2 reactant molecules as they react, the secondary orbital interactions in the endo transition state lowering the reaction barrier energy and make that reaction more kinetically favorable.

Due to the presence of the two oxygen atoms in 1,3-dioxole, the energies of the dienophile fragment orbitals are raised, meaning the cyclohexadiene LUMO and 1,3-dioxole HOMO are now closer in energy and would have the strongest interaction and lead to the most energetically favourable bond formation. Therefore, this is a inverse electron demand Diels-Alder reaction, as a normal electron demand would require the cyclohexadiene HOMO and 1,3-dioxole LUMO to have the strongest interaction.

Nf710 (talk) 15:04, 10 February 2017 (UTC) Why do the oxygens do this?

Energies

	Energies (kJ/mol)
	Exo	Endo
Ea	165.973	158.674
ΔG	-64.945	-71.971

The reaction barriers and reaction energies for both the exo and endo reaction pathways were calculated and are displayed in the table above. By looking at the figures, we can see that the exo pathway has a higher reaction barrier, but lower reaction energy, which corresponds to the thermodynamic product. The endo pathway meanwhile, displays a reaction path with a lower reaction barrier and higher reaction energy, making it the kinetic product. It should be noted that the 2 reactants were taken at infinite seperation, leading to a value of 0 kJ/mol for the energy of the reactants.

Energy profile of the Diels-Alder reaction between Cyclohexadiene and 1,3-Dioxole

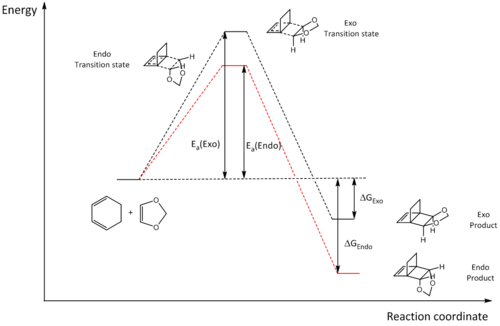NO! your energies are correct. The endo is both the thermo and kenetic. Why would the endo be the kenetic?

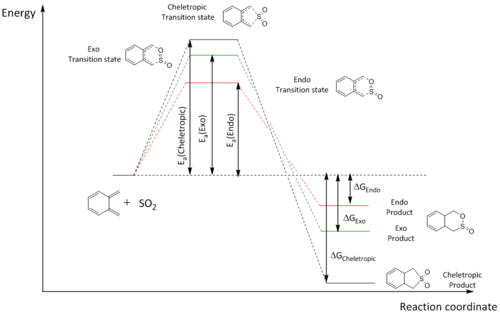
Exercise 3: Diels-Alder vs Cheletropic

The reaction between o-xylyene and SO₂ is a highly interesting one, as it can either proceed in a variant of the standard Diels-Alder reaction (hetero-Diels-Alder), or by a cheletropic reaction. A cheletropic reaction is a subclass of a cycloaddition reaction, with the main difference from a regular cycloaddition being that the two new bonds that are formed are formed to the same atom. This results in the possibility of either the cheletropic, exo, or endo product being formed. In this exercise, all 3 reactions were studied using calculations at the PM6 level. The figure below sums up all the possible reaction pathways.

Reaction scheme

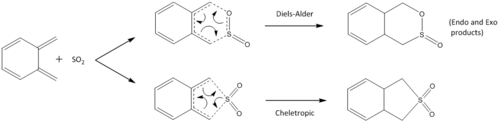Intrinsic reaction coordinates

Reaction pathway	IRC	IRC Graph
Cheletropic
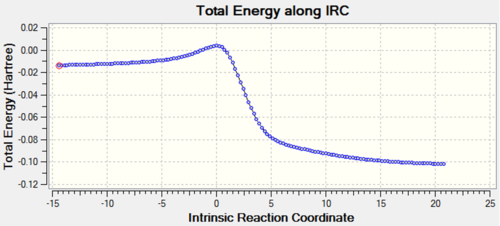Endo Diels-Alder
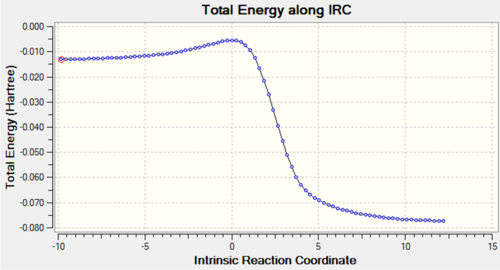Exo Diels-Alder

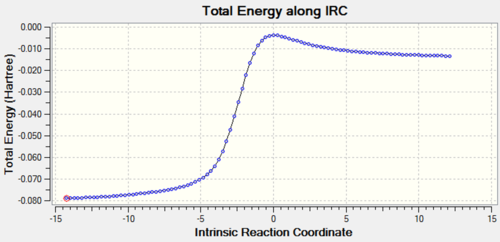The animated GIFs for the IRCs above show the formation of the transition states for the 3 possible reactions, and allow us to determine whether the transition state is formed in a synchronous or asynchronous fashion. The cheletropic transition state can be seen to form in a synchronous fashion, with the 2 C-S bonds forming at the same time. In the endo GIF, the transition state can be seen to form the C-O bond first, followed by the formation of the C-S bond shortly after. This suggests a asynchronous formation of the transition state.

From the IRCs, we can see that the 6-membered rings becomes aromatised over the course of all 3 reactions, which contributes to the stability of the end products and acts as a driving force for the reactions, lowering the energy of the products and accounting for the instability of o-xylylene.

	Energies (kJ/mol)
	Exo	Endo	Cheletropic
Ea	83.963	78.948	103.831
ΔG	-101.159	-100.755	-156.954

(What did you use for your reactants? Tam10 (talk) 12:06, 8 February 2017 (UTC))

The table above summerises the activation and gibbs free energies for all 3 possible reactions that could occur. The endo Diels-Alder product was determined to be the kinetic product as the endo reaction had the smallest activation energy. The reaction leading to the exo Diels-Alder product was found to have higher activation energy than the endo reaction, most likely due to the lack of possible secondary orbital interactions in the exo pathway.

(How do you know there are only 3 possible reactions? If you read further down the script in the additional section there are at least 3 others Tam10 (talk) 12:06, 8 February 2017 (UTC))

The cheletropic reaction has the highest activation energy of the 3, but results in a product that has the lowest energy, making it the thermodynamic product.

Energy profile of the Diels-Alder//Cheletropic reaction between o-Xylylene and SO2

Conclusion

In this laboratory, computational methods were used to study the reaction pathways and transition states of Diels-Alder reactions. By generation of the HOMOs and LUMOs for a reaction, they could be characterised as either a normal or inverse electron demand reaction. Additionally, the reaction pathways could be characterised as being under either kinetic or thermodynamic control depending on the activation energy, and the Gibbs free energy of the reaction.The approach of the reactants during the reaction was found to have large implications on the structures of the transition states along with the final reaction products.

For the reaction of Butadiene with Ethylene, calculations of the MOs analysis provided that the reaction is an example of a standard Diels-Alder reaction. Analysis of the vibrations established that the bonds form synchronously.

In the reaction of Cyclohexadiene and 1,3-Dioxole, analysis of the energies of the transition states and products for the endo and exo paths provided a way in which the thermodynamic and kinetic products could be distinguished. The exo product was found to be the thermodynamic product, with a reaction pathway that gave a more stable product, but also had a higher activation energy corresponding to a higher reaction barrier. The endo product was found to be the kinetic product, with a reaction pathway that gave a less stable product that had a lower reaction barrier than the exo reaction pathway.

In Exercise 3, the cycloaddition of o-Xylylene and SO₂ was investigated. The cheletropic pathway was found to be the thermodynamically favoured reaction path, while the Diels-Alder pathway was the kinetically favoured one. The Diels-Alder pathway has 2 possible products, the endo and exo forms, and for this particular reaction, the endo product was determined to be the kinetic product, while the exo product was the thermodynamic product.