Rep:Mod:moduletwo
Module 2: Inorganic Lab
Preliminary exercises
Optimisation of BH3
GaussView is a graphical interface that is able to display in visual form the results of the program Gaussian, which in turn is used to manipulate molecules. Using The two programs in conjuction, we can simulate a wide range of molecules and predict many properties with a good degree of approximation. The first of such experiments is the optimisation of BH3.
First, a molecule of BH3 was built using the fragments already provided by the program.
The bond length of the molecule, orginally set to be 1.18 Å, was modified to 1.5 Å and the molecule submitted to Gaussian for Geometry Optimisation. The bond length was set to 1.192 and the bond angle to 120°. This is the result of the calculation, as taken from the summary output of GaussView:
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: 3-21G
- Energy: -26.46 a.u. or hartree
- Gradient: < 0.00001
- Dipole Moment: 0.0 Debye
- Point Group: D3H
- Time Taken: 32 seconds
Being a simple molecule (few atoms) and being already in a state quite close to the ideal, the calculation was possible in a very short amount of time, and only five steps were necessary to reach the optimised geometry, as the graphs show:
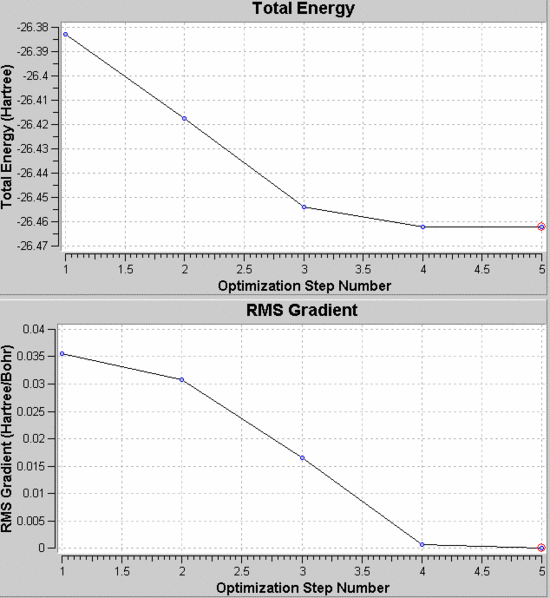
The first graph shows the energy decrease as more steps are carried. The second shows the decreasing gradient, which refers to the gradient in the Potential Energy Surface diagram. The energy is highest when the molecules are too far apart or too close; when the distance is just right, the energy is at a minimum and the gradient is equal to 0. Gaussian calculates to decrease this as close as it can to 0.
Then the MOs of BH3 were calculated. The file is stored here. With this job, we are able to visualise the MOs of the molecule in question. Shown below are the first five MOs in ascending order of energy. The third and fourth are the MOs.
 |
 |
 |
 |
 |
The calculated results are in good accordance with MO theory. This is a diagram of the MO bonding for BH3.
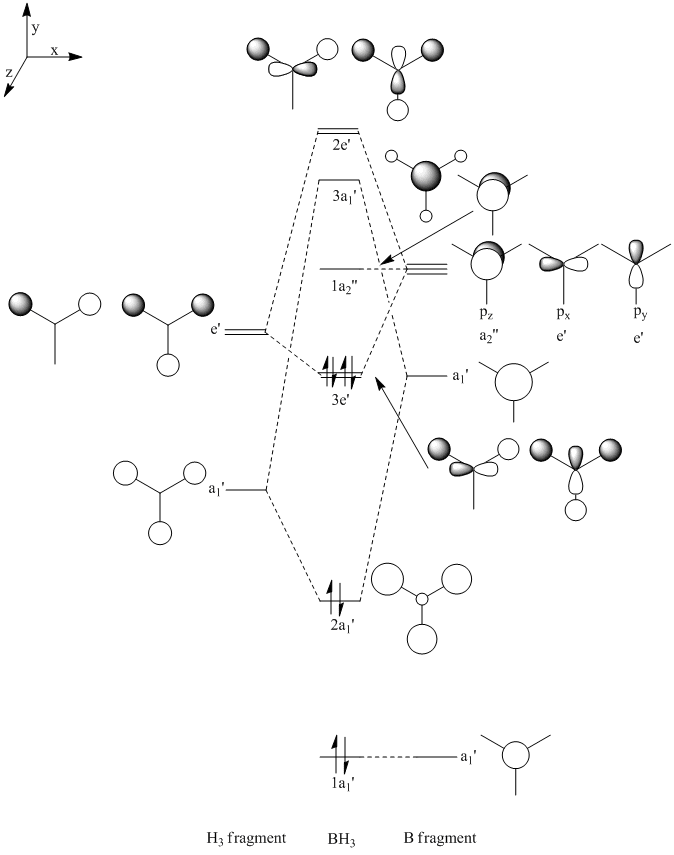
As you can see, the four occupied orbitals and the LUMO have geometries very similar to the ones calculated.
The vibrational modes of the molecule were calculated next. The log fire is stored here.
| Visual Diagram | Frequency /cm-1 | Intensity /arbitrary units | Symmetry Label |
|---|---|---|---|
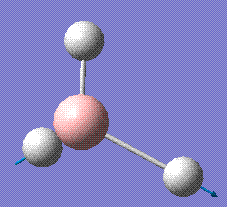
 |
1145.71 | 92.7 | A2'' |
 |
1204.66 | 12.39 | E' |
 |
1204.66 | 12.38 | E' |
 |
2592.79 | 0 | A1' |
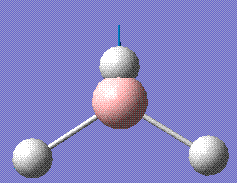
 |
2731.31 | 103.83 | E' |
 |
2731.31 | 103.83 | E' |
The calculation also produced an IR graph.
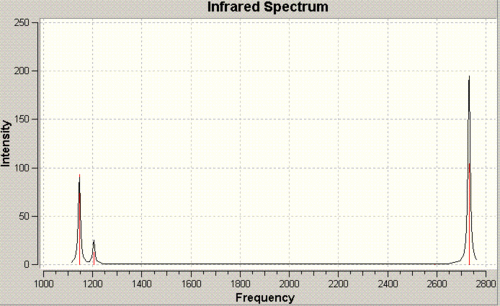
Despite the six vibration modes, there are only three peaks. That's because 2 and 3 are degenerate, as are 5 and 6, and have the same peak. 4 doesn't cause a change in the overall dipole of the molecule and thus doesn't have any intensity and doesn't show on the graph.
Analysis of BCl3
Following the same method as used to analyse BH3, BCl3 was also analysed and optimised. The starting geometry was costrained to D3h (very tightly), the B-Cl bond length was 1.87 Å, and the Cl-B-Cl bond angle was 120° .
This is the summary of the calculation:
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: LANL2MB
- Energy: -69.44 a.u. or hartree
- Gradient: < 0.0001
- Dipole Moment: 0.0 Debye
- Point Group: D3H
- Time Taken: 16 seconds
The new optimised bond length is 1.866 Å, while the overall geometry of the molecule hasn't changed, i.e. it is still trigonal planar with 120° angles. This is not in very good accordance with the reference value of 1.72.[1]
The vibrational modes of BCl3 were calculated then. They were found to be largely similar, as it should be expected due to the identical geometry of the molecules, to the vibrational modes of BH3.
| Visual Diagram | Frequency /cm-1 | Intensity /arbitrary units | Symmetry Label |
|---|---|---|---|
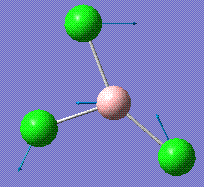 |
214.13 | 3.93 | E' |
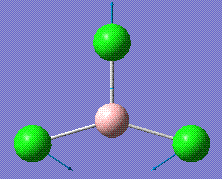 |
214.13 | 3.93 | E' |
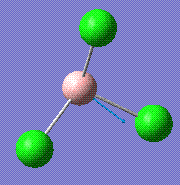 |
376.94 | 43.78 | A2'' |
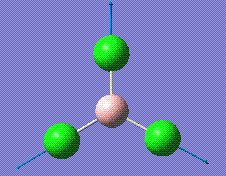 |
417.38 | 0 | A1' |
 |
939.47 | 258.69 | E' |
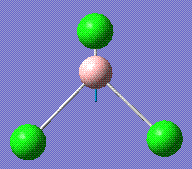 |
939.47 | 258.69 | E' |
A bond is an interaction between two nuclei that adds to the stability of both and is usually characterised by the sharing of electrons in molecular orbitals created by the interaction of the individual atoms' atomic orbitals. The details of the bonding, such as the number of electrons, the contributions of the atomic orbitals, the source of the electrons and the number of nuclei involved may vary in each case. GaussView is largely concerned with nuclei, and hence bonds are only fictitious stick interactions. They only exist in the program in order to costrain what the minimum distance between two nuclei can be.
Isomers of Mo(CO)4L2
Introduction
By using the same methods applied in the exercises above, we can analyse molcules even more complex. By fully optimising a structure, we are able to gain information regarding its stability. If we compare two possible products of a reaction, we can then predict which is preferred. If we compare two isomers, we can determine which one is the most favourable.
The molecule used in this part is going to be Mo(CO)4L2, a metallic complex. It can assume two forms, one where the L ligands are trans, and one where they are cis to each other. By optimising the two structures, we can prove which one has the lowest energy, and choose it as the most stable isomer.
L is, in this case, triphenylphosphine, PPh3, but that would prove too big and complex for Gaussian to handle in a short amount of time. Hence we are going to substitute Cl atoms for phenyl groups, as they have proven to simulate them adequately in terms of electrons and charge distribution.
Optimisation and Frequency Calculations
The first step was to build the molecules in question. They were then loosely optimised using a fairly inaccurate basis set which is, however, quick and gives a good basis for further optimisations.
This is the summary for the partially optimised cis form:
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: LANL2MB
- Energy: -617.55 a.u. or hartree
- Gradient: < 0.0001
- Dipole Moment: 8.62 Debye
- Point Group: C2V
- Time Taken: 15 minutes, 11 seconds
This is the summary for the partially optimised trans form:
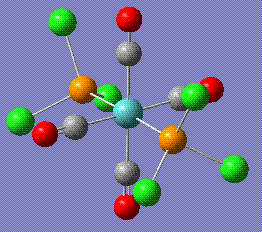
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: LANL2MB
- Energy: -617.52 a.u. or hartree
- Gradient: < 0.0001
- Dipole Moment: 0.08 Debye
- Point Group: D4H
- Time Taken: 38 minutes, 11 seconds
These structures were then optimised again using a stricter and better basis set.
This is the summary for the fully optimised cis form, stored here:
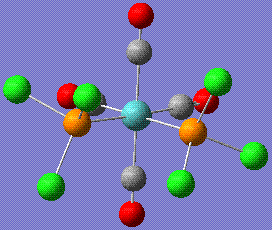
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: LANL2DZ
- Energy: -623.577 a.u. or hartree
- Gradient: < 0.0001
- Dipole Moment: 1.31 Debye
- Point Group: C2V
- Time Taken: 40 minutes, 41 seconds
This is the summary for the fully optmised trans form, stored here:
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RB3LYP
- Basis Set: LANL2DZ
- Energy: -623.576 a.u. or hartree
- Gradient: < 0.0001
- Dipole Moment: 0.3 Debye
- Point Group: D4H
- Time Taken: 35 minutes, 53 seconds
From these calculations, we can then conclude that the cis form is lower in energy that the trans form by about 1 kJ, and therefore should be the preferred isomer. However, literature shows that the trans product is more readily formed[2], and that the bonds and angles are quite different from the experimentally determined data[2] [3]. We can impute the inconsistencies to the inaccuracy of the basis set used: from discussion with co-workers it was revealed that indeed using better basis sets that incorporate the d-orbitals in the calculations yields the correct qualitative result. Another factor of error is the approximation of the phenyl group with a chlorine atom, which surely has repercussions on the entire calculation, expecially regarding sterics.
The cis/trans isomerism is a balance between different effects. Steric repulsion may make a trans complex more favourable, and the favourable dipole created when two ligands are cis may also generate stability. In this case, consulting the literature, it appears as if the steric repulsion between the bulky PPh3 groups predominates.
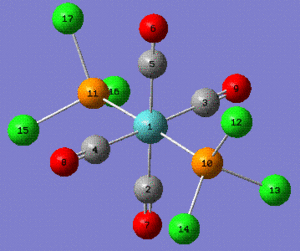
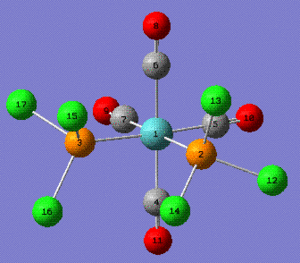
| Trans Mo(CO)4(PPh3)2 selected bonds lengths (Å) | ||
| Bond | Reference Value[3] | Calculated Value |
|---|---|---|
| Mo-P | 2.5 | 2.45 |
| Mo-C(2) | 2.016 | 2.06 |
| Mo-C(3) | 2.005 | 2.06 |
| P-C(Average) | 1.84 | 2.24 |
| C(2)-O | 1.16 | 1.17 |
| C(3)-O | 1.16 | 1.17 |
| Trans Mo(CO)4(PPh3)2 selected angles (°) | ||
| Angle | Reference Value[3] | Calculated Value |
| P-Mo-P | 180 | 177.38 |
| P-Mo-C(2) | 92 | 88.69 |
| P-Mo-C(3) | 87.2 | 90.07 |
| C(2)-Mo-C(3) | 92.1 | 90.5 |
| C(2)-Mo-C(5) | 180 | 179.99 |
| C(3)-Mo-C(4) | 180 | 179 |
| Cis Mo(CO)4(PPh3)2 selected bonds lengths (Å) | ||
| Bond | Reference Value[2] | Calculated Value |
|---|---|---|
| Mo-P(2) | 2.58 | 2.51 |
| Mo-P(3) | 2.58 | 2.51 |
| Mo-C(5) | 1.97 | 2.01 |
| Mo-C(7) | 1.97 | 2.01 |
| Mo-C(4) | 2.06 | 2.06 |
| Mo-C(6) | 2.02 | 2.06 |
| P-C(Average) | 1.83 | 2.24 |
| C(5)-O | 1.15 | 1.18 |
| C(7)-O | 1.16 | 1.18 |
| C(4)-O | 1.14 | 1.17 |
| C(6)-O | 1.14 | 1.17 |
| Cis Mo(CO)4(PPh3)2 selected angles (°) | ||
| Angle | Reference Value[2] | Calculated Value |
| P-Mo-P | 104.62 | 94.14 |
| P(2)-Mo-C(4) | 94 | 89.18 |
| P(2)-Mo-C(5) | 80.6 | 89.41 |
| P(2)-Mo-C(6) | 90.3 | 91.94 |
| P(2)-Mo-C(7) | 163.7 | 176.09 |
| P(3)-Mo-C(4) | 90.6 | 91.94 |
| P(3)-Mo-C(5) | 173.2 | 176.09 |
| P(3)-Mo-C(6) | 84.4 | 89.18 |
| P(3)-Mo-C(7) | 91.7 | 89.41 |
| C(4)-Mo-C(5) | 93.4 | 89.75 |
| C(4)-Mo-C(6) | 174.1 | 178.35 |
| C(4)-Mo-C(7) | 87 | 89.06 |
| C(5)-Mo-C(6) | 93.4 | 89.06 |
| C(5)-Mo-C(7) | 83 | 87.08 |
| C(6)-Mo-C(7) | 90.1 | 89.75 |
Note: the P-C bond length were taken to be P-Cl for the calculated value.
The next step was to calculate the vibrational modes of the two fully optimised molecules. The resulting IR graphs are below, cis and trans, respectively, while the .log files are stored here for the cis form and here for the trans form.
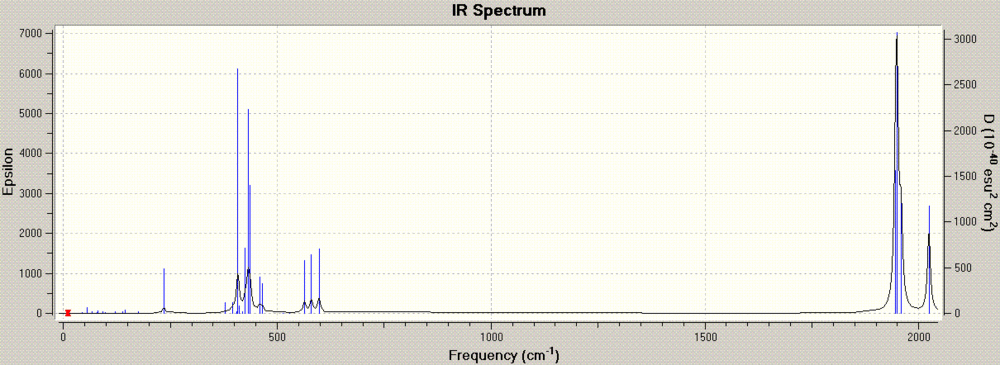
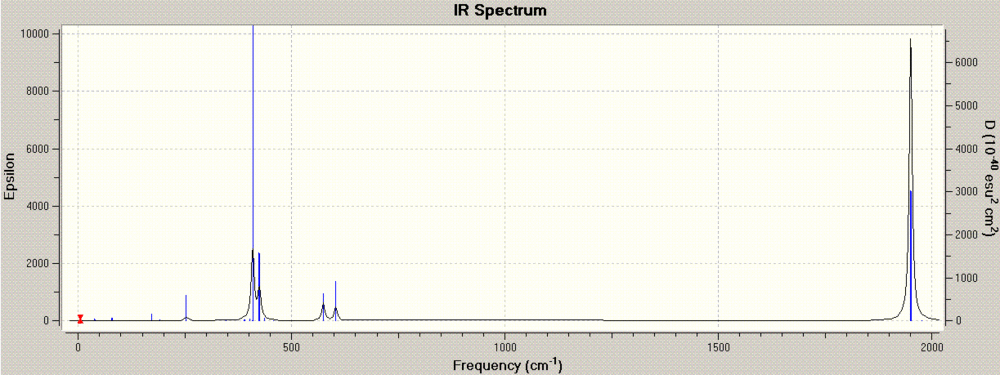
The strongest modes are those that give rise to an overall change in dipole, and therefore we can expect that the stretches involving the movement of the C=O double bond to have higher intensities. Similarly, we can expect the cis form, which doesn't have as much symmetry as the trans form, to have more IR active stretching frequencies. Indeed, we can expect 3 vibrational modes for C=O in the cis form and 1 in the trans form[4][5]. The computed C=O stretches occur at 2023, 1958, 1949 and 1945 cm-1 for the cis form and 1951 and 1950 cm-1 for the trans form, in apparent contradiction with theory. This is because the geometry is, in this case, non costrained to the native C2v (cis) and D4h (trans) point groups. If the calculation were more precise, we would be able to have the precise number of stretches. We can already see that the trans frequencies are very close and hence they present one overall peak, despite being two distinct vibrational modes. The cis frequencies approximate the literature values of 2023, 1927, 1908, 1897 cm-1[6].
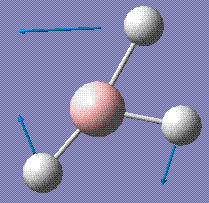
There are some very low frequency vibrations that are related to the rotation of the P-Mo bonds.
| Visual Diagram | Frequency /cm-1 | Wavelength /nm | Molecule |
|---|---|---|---|
 |
10.78 | 927643 | Cis |
 |
17.68 | 565610 | Cis |
 |
4.91 | 2036659 | Trans |
 |
6.14 | 1628664 | Trans |
Note: the P-Cl bonds are missing because Gaussian removes them and I was unable to add them and display the vibration at the same time.
These vibrations occur at an extremely low energy, many times inferior to the energy at room temperature. where they will, therefore, occur very quickly.
Mini-Project: Homopolyatomic Clusters of Nitrogen
Introduction
Homopolynuclear clusters of nitrogen are a class of theoretical compounds that present considerable interest as HEDM (High Energy Density Material) and hence the possible application as fuels and similar. This property derives largely from the stability of the N-N triple bond present in diatomic nitrogen gas, which would be an excellent and probably exothermic driving force behind the decomposition of a homopolynuclear cluster such as N6. This study has the purpose of determining the most likely structure of the N6 cluster, hexaazo.
Preliminary calculations
All calculations are carried with DFT/B3LYP method and 6-31G(d) basis set.
As suggested by the literature[7] it is useful, before calculating the clusters proper, to determine the energies of the nitrogen fragments. In particular, the N2 diatomic is quite important in the analysis of the cluster and hence its properties should be found first. The optimisation yielded a N2 with bond length of 1.10 Å (lit. value[8] 1.10 Å), energy of -109.52 a.u. and IR stretching frequency at 2457 cm-1 (lit. value [9] approx 2335 cm-1). The calculated bond enthalpy, taken to be equal to E(Dinitrogen)-2×E(Single atom nitrogen), was 1470 kJmol-1 (Lit. value[8]: 944 kJmol-1). N2H2 and N2H4, which correspond to a N=N double bond and to a N-N single bond, respectively, were also calculated. It was found that the most stable form of N2H2 is when the hydrogens are trans to each other (-110.64 a.u. against -110.63 for the cis conformation and -110.44 for the linear conformation) and that the bond length for a N=N double bond is 1.26 Å (1.24 cis, 1.22 linear, 1.20 lit. value[8]). N2H4 was found to have a N-N single bond length of 1.44 (1.46 lit. value[8]) and overall energy of -111.86 a.u..
Stability Calculations
A number of possible structures for N6 was submitted to Gaussian. In particular, all the conformations suggested in literature[7] were tested. However, with this basis set only the benzene like structure was found to be stable; Dewar benzene, benzvalene, prismane and bicyclopropane either failed or reverted to three individual dinitrogen molecules. Cyclohexane-like conformations of chair, boat and twist-boat were also submitted as well as linear forms. The equivalent forms of methylcyclopentane and smaller rings with extruding nitrogen atoms were submitted.
Analysis
This table represents the stable conformations of N6 found with this study:
| Molecule | Energy (relative to the most stable form)/kJmol-1 | Notes | HOMO and LUMO |
|---|---|---|---|
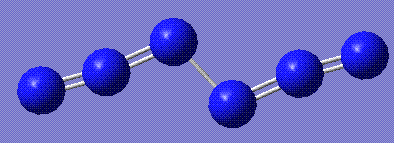 |
0 | Diazide form. Any non completely linear precursor converges to this form. Stored here. | 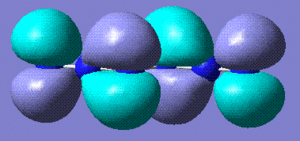  |
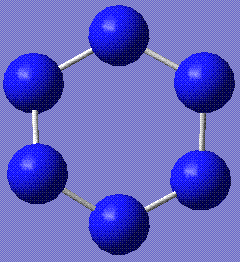  |
+110.25 | Cyclohexane, in both chair and boat conformations, stabilises to this slightly twisted ring. Twist boat does not stabilise. Stored here (boat derivative) and here (chair derivative). | 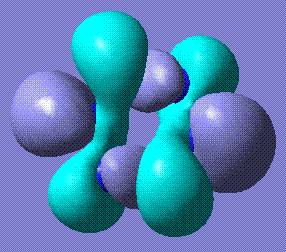  |
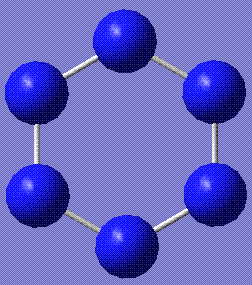  |
+120.75 | The benzene form stabilises to this structure. It is completely planar. Stored here | 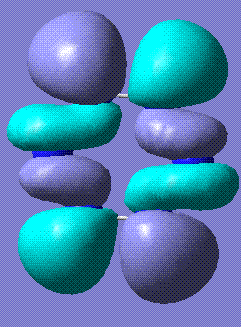 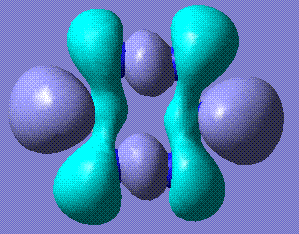 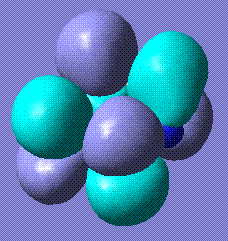 |
 |
+333.375 | Completely linear, it only stabilises from completely linear precursor. Stored here | 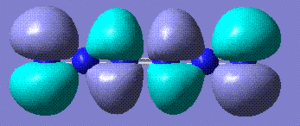 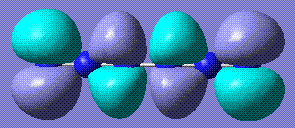 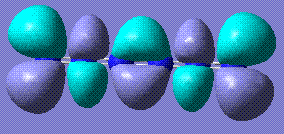 |
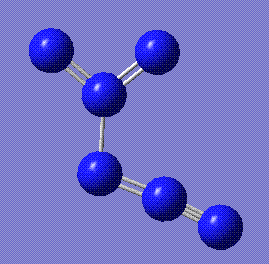 |
+346.5 | Derived from the all-nitrogen analogue of 1,3 Dimethylcyclobutane. Stored here. | Due to problems with Gaussian, the MOs were not calculated. |
The most stable form appears to be the diazide. The bond lengths are consistent with the azide single molecule (stored here)(1,2 N-N in diazide: 1.14 Å, 1.12 Å in azide; 2,3 N-N in diazide: 1.25, 1.20 in azide).
The completely planar form has bond lengths of 1.32 Å, which are between triple and single bonds. This suggests a conjugated benzene-like system, which perhaps contributes to the stability of the molecule. Comparison with benzene HOMO and LUMO reveals that the LUMOs of the two molecules are very similar.

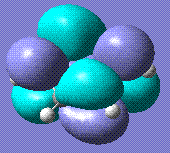
The HOMO/LUMO analysis of the cyclic and twisted cyclic forms of N6 reveal that the orbitals are very similar. In fact, they appear to be the same, except that in twisted cyclic the bending of the overall molecule allows the orbitals to overlap and merge. This is evident in the HOMO, Perhaps this allows the extra stabilisation that makes this conformation lower in energy.
The frequency analysis (stored here for linear, here for the diazide, here for the cyclic, here for the twisted cyclic and here for the isodiazide) reveals that in fact the linear form is not fully optimised, and hence most likely not fully stable using this basis set. There are several negative frequency vibrations that indicate this. The other four forms are instead fully converged and show only positive frequencies. The only exception is the cyclic form, which shows one negative frequency. It is very likely that tinkering with the molecule to improve the optimisation will yield the twisted cyclic form. The diazide shows very intense peaks when the terminal N-N bonds, which seem to be triple bonds from comparison with dinitrogen, are excited. This almost proves the nature of these bonds, as the frequency involved is very high, hence it has high energy, like a N-N triple bond.
The isodiazide structure was perhaps the most surprising result. In an effort to identify as many possible different forms of N6, several fairly exotic structures were submitted to SCAN, but the inherent instability of the starting cluster made it unlikely that any of them would come back positive. But in fact the 1,3 dimethylcyclobutane analogue and the propylcyclopropane analogue came back as having a stable form. While the latter was then revealed to have a negative frequency, the former had only positive values and was therefore a legitimate isomer of N6. It is closely related to the structure of the diazide, where the linkage is between the terminal nitrogen of one and the middle nitrogen of the other. Bond lengths are consistent with reported N-N values. Its energy is fairly high, though, indicating that this is not the preferred form.
In conclusion, N6 shows, at this level of calculation, two main forms: diazide and twisted cyclic. A third possible form is isodiazide.
References
- ↑ Branchadell, V.; Oliva, A.; J. Chem. Am. Soc., 1991, 113, 4132-4136, DOI:10.1021/ja00011a011
- ↑ 2.0 2.1 2.2 2.3 Cotton, F. A.; Darensbourg, D. J.; Klein, S.; Kolthammer, B. W. S. Inorg. Chem., 1982, 21, 294-299 DOI:10.1021/ic00131a055
- ↑ 3.0 3.1 3.2 Hogarth, G.; Norman, T. Inorg. Chim. Acta, 1997, 254, 167–171DOI:10.1016/S0020-1693(96)05133-X
- ↑ Darensbourg, D.J.; Darensbourg, M.Y. J. Chem. Edu., 1970, 47, 33-35
- ↑ Cotton, F. A.; Kraihanzel. C. S., J. Am. Chem. Soc., 1962, 84, 4432 DOI:10.1021/ja00882a012
- ↑ Darensbourg, D. J.; Kump, R. L., Inorg. Chem., 1978, 17, 2680-2682DOI:10.1021/ic50187a062
- ↑ 7.0 7.1 Engelke, R. J. Phys. Chem. 1989, 93, 5122-5727DOI:10.1021/j100352a016
- ↑ 8.0 8.1 8.2 8.3 Stark, J. G.; Wallace, H. G., Chemistry Data Book, London, 2001
- ↑ Lubezky, A.; Kozirovski, Y.; Folman, M., J. Phys. Chem., 2002, 97, 1050-1054DOI:10.1021/j100107a012
