Rep:Mod:moduletthree
Module 3
Cope Rearrangement
The purpose of this tutorial is to learn the basics of GaussView and Gaussian in order to fully understand the dynamics of the Cope Rearrangement. This entails optimising the transition state, finding out the energies and determining the analogue structures.
Preliminary Calculations
As an exercise, two conformations of 1,5 hexadiene were built, one with an anti arrangement along the four central carbons and the other with a gauche arrangement along the same carbons. The two molecules were then optimised using the HF/3-21G method. These then converged to two stable conformers that were then determined to be, comparing with the Appendix 1 Table, anti4 and gauche5, respectively.
Results for the anti optimisation, stored here:
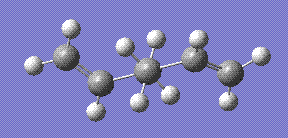
- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RHF
- Basis Set: 3-21G
- Energy: -231.69097 a.u. or hartree
- Gradient: < 0.00001
- Dipole Moment: 0.2956 Debye
- Point Group: C1
- Time Taken: 1 minute, 40 seconds
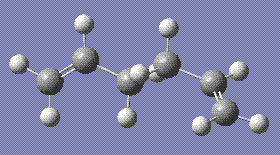
Results for the gauche optimisation, stored here:
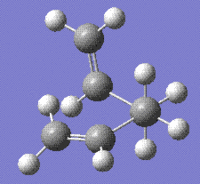

- File Type: .log
- Calculation Type: FOPT
- Calculation Method: RHF
- Basis Set: 3-21G
- Energy: -231.68962 a.u. or hartree
- Gradient: < 0.00001
- Dipole Moment: 0.4439 Debye
- Point Group: C1
- Time Taken: 2 minutes, 24 seconds
Following this, the anti2 conformer suggested by the appendix table was built and optimised using first the HF/3-21G method (here) and then the more accurate B3LYP/6-31G(d) (here). The difference in energies between the two levels of accuracy was quite noticable. While the first method predicted an energy of -231.69 hartree, the second one gave back -234.61 hartree. This constitutes a difference of about 2000 kJ/mol. A frequency calculation (here) proved that it was indeed a minimum, as there were no negative frequency vibrations. A number of data was collected and stored for future use:
- Sum of electronic and zero-point Energies: -234.469187
- Sum of electronic and thermal Energies: -234.461836
- Sum of electronic and thermal Enthalpies: -234.460892
- Sum of electronic and thermal Free Energies: -234.500779
Optimising the Chair Transition State of the Cope Rearrangement
The Cope Rearrangement is an example of a [3,3] sigmatropic pericyclic reaction. In this case, we are observing the rearrangement of electrons in 1,5 dihexene that occurs following this scheme:
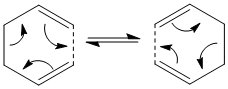
It can proceed through two intermediate species that resemble the conformers of cyclohexane, the chair structure and the boat structure.
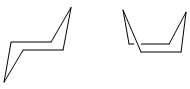
Using different methods, we are able to calculate the transition states for the two mechanisms. Once the two structures have been reached, then they can be compared in terms of energy and determine which conformer of 1,5 dihexane do they derive from. The method used to optimise the chair transition state is the frozen coordinate method. First, we are going to fix (freeze) the distance between the two fragments, which are CH2CHCH2 allyl groups, and optimise the rest of the molecules. When the entire structure is in place, the fragment separation is finally optimised, finally yielding the transition state.
Two allyl groups were placed at a distance of approximately 2.2 Å, because this was known to be approximately the separation between them in the transition state. A first optimisation was run with the HF/3-12G method. The resulting molecule looked like the the structure given in appendix 2 and had an immaginary frequency at -818 cm-1.

At this point the distance between the terminal atoms (where the bonds would be forming and breaking) was frozen to exactly 2.2 Å for both of them. The rest of the molecule was then optimised using the same basis set, and the frozen bonds were optimised after that. This is the resulting structure, stored here:
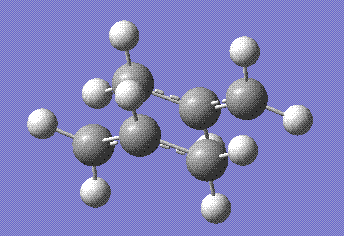
The transition state was then approximated to the closest stable conformer of 1,5 dihexene via IRC calculation. The calculation was set up in the forward direction only and to be carried for 100 steps in order to drive it to completion. After 47 steps a minimum was reached and optimised using the HF/3-12G basis set. This yielded the follwing molecule, stored here:

The energy of the molecule is given as -231.69167 hartree, which is the same as gauche2 from the appendix table. We can therefore conclude that the chair mechanism proceeds from this structure.
Optimising the Boat Transition State of the Cope Rearrangement
The boat transition state was calculated using a different method, called QST2. With this approach, we have the starting reactant and the end product in the same .gjf file, and then Gaussian calculates the intermediate between the two structures. The first step was to arrange the two products so that a Cope rearrangement would occur in order to go from one to the other. This was accomplished by renumbering the atoms and then modifying the geometry to give the following molecules:

This was done after the original configuration, which was more linear, failed. This arrangement allows the transition state to be calculated first using the HF/3-21G basis set, stored here, and then optimised using the B3LYP/6-31G(d) basis set, stored here. This is the final structure:
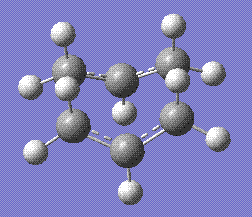
This structure was then submitted for an IRC calculation, in forward direction only and for 100 iterations. The resulting molecule, stored here, was as follows:
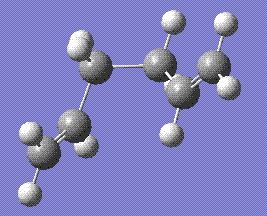
The energy of the structure was -231.69266 hartree, confirming that the boat transition state rises from the gauche3 conformation.
Analysis
| HF/3-21G | B3LYP/6-13G(d) | |||||
|---|---|---|---|---|---|---|
| Molecule | Electronic Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies |
| Chair Transition state | -231.61932 | -231.466701 | -231.461341 | -234.556983 | -234.414925 | -234.409005 |
| Boat Transition state | -231.6028 | -231.450931 | -231.445301 | -234.543092 | -234.402325 | -234.395991 |
| Anti2 | -231.69253 | -231.539540 | -231.532567 | -234.611718 | -234.469187 | -234.461836 |
The reported values are in good accordance with the ones given in the appendix. The difference in energy between the anti2 state and the boat transition state is approximately 43 kJ/mol, while the chair transition state is lower in energy, as predicted, being 34 kJ/mol higher. This closely resembles experimental values[1].
Diels Alder Reaction
Introduction
The next reaction we are going to study is the Diels Alder reaction. It is a pericyclic cylcoaddition that results in the formation of a cyclohexene unit from a diene and a dienophile. In order for this to happen, the orbital overlap between the two reactants has to be favourable, i.e. they must have the same kind of symmetry. We define an orbital as symmetric if it has symmetry along the plane of reflection of the overall reaction, which is shown here:
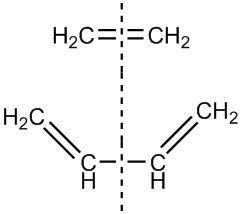
If it doesn't, then the MO is labeled as asymmetric.
Molecular Orbital Calculation
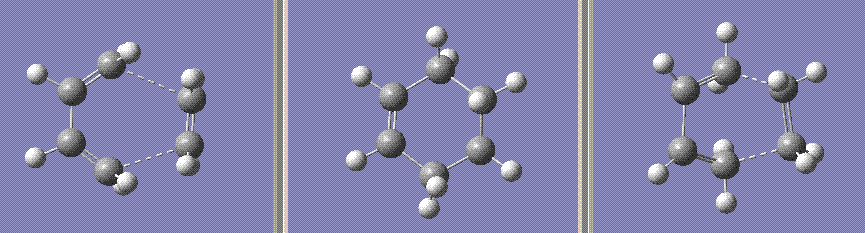
The two molecules in question, cisbutadiene and ethene, were drawn and optimised using the HF/3-21G basis set. The MOs were then visualised from the optimised structures. The HOMOs and the LUMos are shown below:
| Cisbutadiene HOMO | Cisbutadiene LUMO |
 |
 |
| Ethene HOMO | Ethene LUMO |
 |
 |
As it is evident, the HOMO of cisbutadiene is not symmetric looking down the central axis, while its LUMO is. Inversely, the HOMO of ethene is symmetric and the LUMO isn't. Hence we can predict that the reaction will proceed either with the HOMO of the cisbutadiene reacting with the LUMO of the ethene or with the HOMO of the ethene reacting with the LUMO of the cisbutadiene.
Transition State Calculation
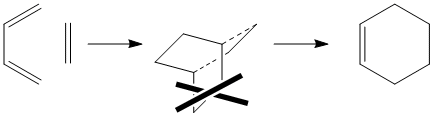
It was decided to use the QST3 approach to reach the transition state for the Diels Alder reaction between cisbutadiene and ethene. This is analogous to the method used to calculate the transition state for the boat conformation. The main difference is that with this calculation, instead of using reactants and product, we use reactants, product and guess for the transition state, as shown here below:
This was based upon the reaction scheme that predicts that the transition state is similar to bicyclo(2.2.2)octene minus an ethane unit.
All the molecules involved were optimised with Semi empirical/AM1 basis set prior to addition to the main input file with the same basis set. This yielded a molecule which had the following structure:
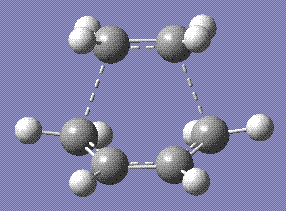
An analysis of the molecular orbitals proved that the reaction proceeds with the HOMO of the cisbutadiene reacting with the LUMO of the ethane, as it is clearly shown here:
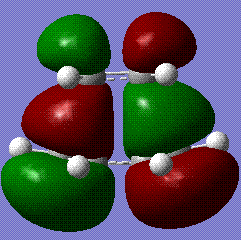
We can therefore conclude that the HOMO at the transition structure is asymmetric, not only from visual analysis, but also when taking in consideration the consituent orbitals from the reactants, which are both symmetric and hence make the reaction allowed.
The bond length, at this level of calculation, is 2.11 Å for both transition bonds. Considering that the Van Der Waals radius of carbon is 1.7 Å [2] and the C-C single bond length is 1.54 Å[3] we can truly affirm that this is a transition state, as it is not quite yet a σ bond, but it is less than the sum of two Van der Waals radii.
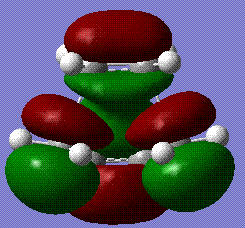
The imaginary vibration at -953 cm-1 displays the reaction: it shows the terminal bonds of cisbutadiene converging towards the atoms of ethene.
Stereoselectivity Analysis
The preceding reaction had no issues of stereoselectivity: all the reactants were perfectly symmetric and only one possible product could be formed. The Diels alder reaction between cyclohexa-1,3-diene and maleic anhydride can instead have two products, denominated endo and exo. The endo product is favoured[4].
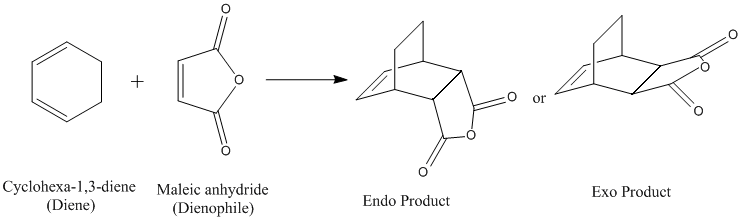
The transition states for the exo and endo reactions were calculated using the frozen coordinate method. Ciclohexa-1,3-diene and maleic anhydride were first built and optimised, then the two molecules were put into the same input file and arranged so that the carbons involved in bond forming would be at a distance of approximately 2.2 Å. In the endo optimisation, the maleic anhydride was orientated so that the -(O=C)-O-(C=O)- unit was facing the diene group, while in the exo optimisation it was facing away from that same group. The bond forming distance was frozen to 2.2 Å using the connection editor while the rest of the molecule was optimised using the Semi-empirical/AM1 method. This yielded a slightly modified complex that was then otpimised again when the bonds were unfrozen, and this yielded the final transition state for both reactions, stored here for the endo and here for the exo:
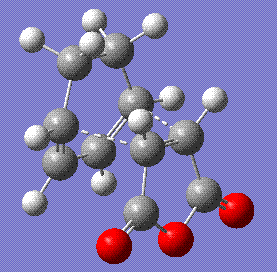 |
 |
The energy of the endo form is -0.0515 a.u. and the energy of the exo form is -0.504 a.u., thereby confirming that the endo is favoured if we assume the reaction to be kinetically controlled. The stability if this form is largely due to the secondary orbital overlap interaction[4] that means that even though the steric clash between the diene unit and the -(O=C)-O-(C=O)- group is unfavourable, the stabilisation gained by the interaction between the empty orbitals of the two groups overcomes this effect and makes this form more favourable. This is clearly shown in the MO analysis. In the endo form, the oxygen orbitals are facing the diene unit and able to interact with its extended system, while in the exo form this is not possible:
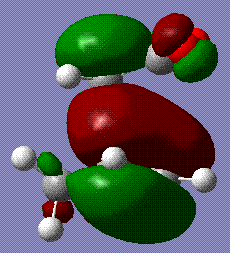 |
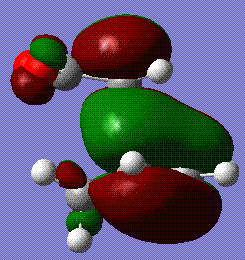 |
This is a table of the most relevant bond lengths:
| Bond | Endo | Exo |
|---|---|---|
| Forming C-C | 2.16 | 2.17 |
| Carbonyl C-opposite C on ring | 2.89 | 2.94 |
| C=C bonds on diene | 1.393 | 1.394 |
| C-C bond in diene | 1.397 | 1.396 |
We can see that the favourable secondary orbital overlap effect puuls the two grouos together despite steric strain. In both cases we cans see the bonds forming and breaking as the double bonds in diene unit lengthen from 1.34 Å[3] and the single bond shortens from 1.54 Å[3] in the process of cycloaddition.
References
- ↑ Goldstein, M. J.; Benzon, M. S., J. Am. Chem. Soc., 1972, 94, 7147 DOI:10.1021/ja00775a046
- ↑ Bondi, A. J. Phys. Chem., 1964, 68, 441–451 DOI:10.1021/j100785a001 .
- ↑ 3.0 3.1 3.2 Stark, J. G.; Wallace, H. G., Chemistry Data Book, London, 2001
- ↑ 4.0 4.1 Fox, M. A.; Cardona, R.; Kiwiet, N. J., J. Org. Chem., 1987, 52, 1469–1474 DOI:10.1021/jo00384a016
