Module 3: The Transition State

Irene Iriarte Carretero, November 2010

Introduction

In this section, two important reactions will be examined using computational methods. The main focus will be placed on finding the transition states for the reactions. The fact that the molecules studied are large, means that the energy cannot be calculated using an analytical function of the atomic coordinates. Molecular mechanics and force field methods cannot be used either, because they do not describe the making and breaking of bonds or the changes in electron distribution. Instead, the methods used are based on molecular orbital theory, which numerically solve the Schrodinger equation and can then analyse the potential energy surface. With this information, one can find the shape of transition structures along with information such as activation energy.

The Cope Rearrangement

The first reaction to be analysed is the Cope rearrangement of 1,5-hexadiene. The main aims of this section are to find the low-energy minima and the transition structure by analysing the potential energy surface of C₆H₁₀. Computational methods helped understand this mechanism, and finally it was agreed that it happens via a concerted mechanism with a "chair" or a "boat" transition structure. This reaction analysis will show this.

Optimisation of Reactants and Products

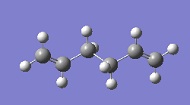
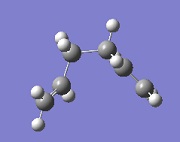
The first step was to optimise the reactants and the products. 1,5-hexadiene can exist in many different conformations (several gauche and several anti).^[1]. A few of these conformers were examined, and the results can be seen in the table below. The main objective was to find an anti and a gauche conformer in order to compare their energies and to find the conformer with the C_i symmetry.

**1,5-Hexadiene Conformers**
Symmetry	Energy (a.u.)	Equivalent structure in app 1
C₂	-231.69260	anti1
C_i	-231.69254	anti2
C₂	-231.69167	gauche2

As one can see, the energies are all fairly similar to each other. However, the anti conformer found had the lowest energy out of the three conformers displayed. This makes sense since the groups are further away from each other. Therefore, the structure with the lowest energy should be the one with C_i symmetry, seeing as all the atoms are as far away from each other as possible. This structure can be seen in the table above. The three conformers above can be compared with the structures given in Appendix 1 in the lab manual. The energies in each case are extremely accurate.

The conformer with the C_i symmetry was reoptimised using a more accurate method (B3LYP/6-31G*) in order to compare the data with the one obtained using the previous optimising method (HF/3-21G). The table below summarises both sets of information.

**Method comparison**
	HF/3-21G	B3LYP/6.31G*
Geometry
Energy	-231.69254	-234.61171
C=C bond length (pm)	132	133
sp2C-sp3C bond length (pm)	151	150
C-C bond length (pm)	155	155
C2-C3-C4-C5 dihedral angle (°)	180	180
C1-C2-C3 dihedral angle (°)	124.8	125.3

The results show that the two structures are almost identical, varying only slightly in bond lengths and bond angles. The energy of the more accurate method is slightly lower, but a comparison cannot be made in this aspect, as the different methods treat the molecule in different ways. The general conclusion is that the HF/3-21G produces good enough results to model 1,5-hexadiene.

A frequency analysis of the molecule was performed in order to make sure that the geometry gave an energy minimum. This was proved because the analysis did not produce any negative (imaginary) frequencies. Some of the most important vibrations can be seen in the table below. In general, it shows that the spectrum is quite similar to the literature result. It is not exactly the same due to the inaccuracies in the method used.

**Vibration analysis**
Vibration	Frequency (cm^-1	Intensity
	939	61
	3031	54
	3080	36
	3136	56
	3155	15
	3233	45

The calculation performed also allows us to find important information on the energy of the molecule. This can be seen below. All energies are given in atomic units.

Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500777

Optimising "Chair" and "Boat" Transition Structures

In this second section, the two different transition structures will be optimised using several different methods. The transition structures consist of two C₃H₅ fragments which are about 2.2 Å apart. However, one has C_2h symmetry while the other one has C_2v symmetry.

Chair Transition State

The first step was to optimise the allyl fragment (HF/3-21G) and once this was completed, to paste two molecules together into one structure which approximated the geometry of the chair transition state. Due to the fact that the guess geometry was a fairly accurate one, the easiest way of optimising the structure was to compute the force constant matrix (Hessian) in the first step of the optimisation and then this is updated as the optimisation proceeds. This was the first method used. Opt=NoEigen had to be added to the calculation, in order to stop the calculation crashing if several imaginary frequencies are found.

The results showed that the transition structure had an energy of -231.6193 a.u. and that it had an imaginary frequency at -818 cm^-1. This proves that the structure is indeed a transition state. This is because the frequency analysis calculates the second derivative of PES. If there is a negative frequency, the structure is a maximum and the structure is therefore a transition state. The vibration was animated to ensure that it indeed represented the Cope rearrangement.

9B

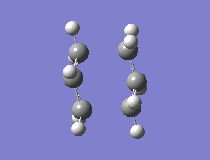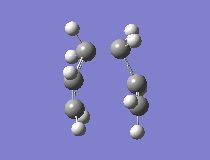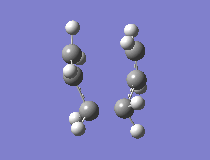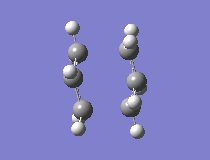The second method used to optimise the structure is normally used for cases in which the starting guess structure is not close to the exact structure. The previous method cannot be used with certainty, because the curvature of the surface may be different at points further away from the transition structure. In this case, the structure is generated by freezing the reaction coordinate and minimising the rest of the molecule in order to get a better starting point by achieving an energy minimum. Once the rest of the molecule is at a minimum, the reaction coordinate is then unfrozen and the transition state can be calculated. This method has an advantage which is that sometimes the whole Hessian does not have to be calculated. Instead, differentiating along the reaction coordinate sometimes gives a reasonable guess for the initial force constant matrix.

This approach indeed gave the same energy as before (-231.6193 a.u.) and the same vibration at -818 cm^-1. This shows that both approaches are accurate and display very similar results.

Boat Transition State

Finally, yet a different method was used to find the boat transition state. This is the QST2, where both the reactants and the products of the reaction are specified. The calculation then interpolates between the two and eventually finds the transition state. This required both molecules to be numbered the same way. The first attempt at this method failed, due to the fact that the structures drawn were too far away from the boat transition state structure and the calculation was therefore not converging. The solution to this was found by modifying the angles in the structure so it looked more similar to the actual transition state. The second attempt showed that the optimised structure was indeed a transition state. Its energy was -231.6028 a.u. and it showed an imaginary frequency at -840 cm^-1 which indeed showed the Cope rearrangement. One can see that the boat transition state lies slightly higher in energy than the boat one.

9B

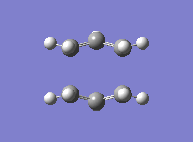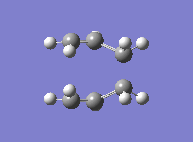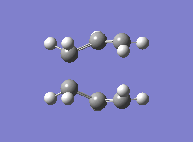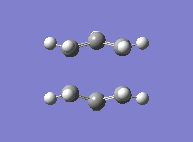IRC: Intrinsic Reaction Coordinate Method

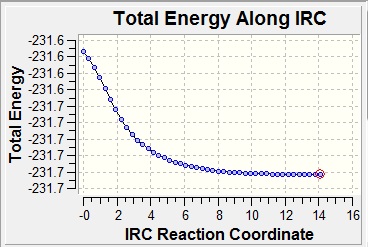
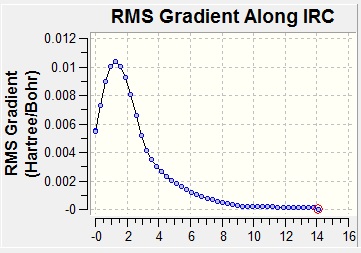
This method works by following the minimum energy path from a transition structure down to the local minimum on a potential energy surface. A set of points is created by taking small geometry steps, always in the direction where the gradient of the energy surface is steepest. This therefore allows you to know what conformer the transition state will lead you to. In this case, it was done with the boat transition state. The first time, this was run in the forward direction, calculating the force constant only once and with 50 steps. The output file of this calculation showed that only 21 steps had been calculated but that this had not converged. After this, there were several options. In the first place, a normal optimisation (B3LYP/6-31G*) was applied on the last structure of the previous calculation. This method was followed and the conformer had a C₂ symmetry and an energy of -231.6107 a.u., which was not close to the lowest energy conformers. The second option was to restart the IRC calculation, only specifying a larger number of points until it does reach a minimum. Finally, the third option was to redo the IRC computing the force constant at every step. This was also computed and the result was a conformer with C₂ symmetry with an energy of -231.6917 a.u., which corresponds to the gauche2 conformer in the appendix mentioned before. The IRC analysis can be seen below. One can see how the gradient of the PES approaches zero at the end of the analysis, meaning that the energy is at a minimum and there is therefore a low energy conformer. One can also see the energy approaching the value given.

IRC Reaction Coordinate	RMS Gradient

Activation Energies

The activation energy for the process can be calculated after having found the transition state by finding the energy between the reactant (conformer with C_i symmetry) and the transition state. In this case, we can compare the activation energies of the reaction via the boat and the chair transition states. In order to do this accurately, all the molecules involved were reoptimised using the B3LYP/6-31G* method. The table below summarises the results. From the results, one can see how the second and more accurate method used provided results in good agreement for experimental values. ^[2]

Summary of energies (a.u.)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.6193	-231.4667	-231.4613	-234.5527	-234.4150	-234.4090
Boat TS	-231.6028	-231.4509	-231.4453	-234.5431	-234.4023	-234.3960
*Reactant (anti2)*	-231.6925	-231.5395	-231.5326	-234.6117	-234.4693	-234.4619

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.7	44.7	34.1	33.2	33.5 ± 0.5
ΔE (Boat)	55.6	54.7	42.0	41.3	44.7 ± 2.0

Diels-Alder Cycloaddition

In this section, two examples of Diels-Alder cycloaddition reactions will be examined. This is a concerted pericyclic reaction, in which the п orbitals of the dienophile are used to form new σ bonds with the π orbitals of the diene. The HOMO and the LUMO of the reactants play a very important role in these reactions and computational techniques allow us to investigate this further.

Whether a reaction is allowed or forbidden depends on the number of π electrons involved. The HOMO or the LUMO of one reactant interacts with the HOMO/LUMO of the other fragment to form two new bonding and anti-bonding molecular orbitals. If the HOMO of one fragment can interact with the LUMO of the other, then the reaction is allowed. They can only interact if there is a significant overlap between them, and if the orbitals have different symmetry properties, there is no overlap and the reaction is therefore not allowed.

The substituents on each reactant can affect the reaction and this will be investigated further in the second reaction examined.

Prototype reaction

The first reaction examined is the prototype Diels-Alder reaction between ethylene and butadiene. The first step was to optimise the cis butadiene reactant using the AM-1 semi-empirical molecular orbital based method and the HOMO and the LUMO of this reactant was analysed. The results can be seen below.

The molecular orbital analysis of ethylene shows that the HOMO is symmetric with respect to the reflection plane, while the LUMO is antisymmetric. Therefore, the reaction is fully allowed, as their HOMOs can interact with their LUMOs because they have the same symmetry.

**Molecular Orbital Analysis of reactants**
	Symmetry	Energy (a.u.)
HOMO cis-butadiene	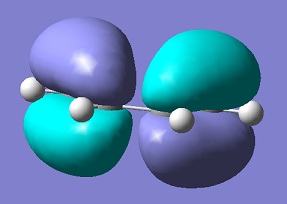a	-0.344
LUMO cis-butadiene	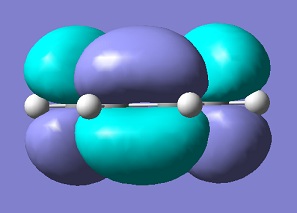s	0.0170
HOMO ethylene	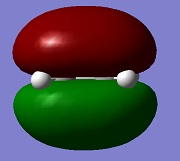s	-0.388
LUMO ethylene	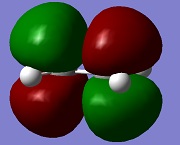a	0.0528

The next step was to find the transition state. This was done through the freeze coordinate method, to account for the fact that the guess transition state might not have been very close to the real geometry of the transition state. The bonds were frozen to 2.2A and the result was then optimised to a TS(Berny). The transition state obtained can be seen below. To ensure that the structure was indeed a transition state, a frequency analysis was calculated. There was a single imaginary frequency at -956 cm^-1. This frequency shows the synchronous formation of two C-C bonds.

The average bond length between two sp³ carbons is of 1.54A ^[3] while the average bond length between two sp² is 1.33 A ^[4]. In the transition state proposed, the C=C bond is 1.38 A, while the C-C bonds are 1.39 A. This value is between the average lengths mentioned before, which clearly shows that the π bond is being made into a σ one (it is lengthening). The Van der Waals radius for carbon is of 1.7 A and the bond length between the newly formed carbon bonds was of 2.12 A. This value is less than twice the Van der Waals radius for carbon, which means that they are close enough together to share electron density.

The molecular orbitals of the transition state can be seen below.

**Molecular Orbital Analysis of transition state**
	Pictorial representation	Symmetry	Energy (a.u.)
HOMO		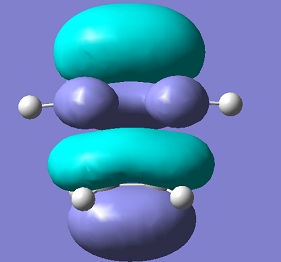s	-0.0108
LUMO		s	0.0107

From the pictures, one can see that the HOMO of the transition state is made from the combination of the cis-butadiene HOMO and the ethylene LUMO. The LUMO comes from the overlap of the cis-butadiene LUMO and the ethylene HOMO. This agrees with the rules stated before.

Below one can see the transition structure and the animated vibration.

9B

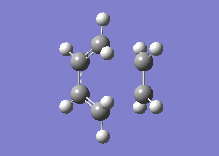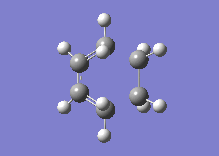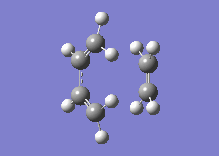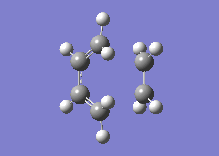Diels-Alder of Cyclohexa-1,3-diene and Maleic Anhydride

In the second part of this exercise, the regioselectivity of the Diels-Alder reaction will be examined by looking at the reaction between cyclohexa-1,3-diene and maleic anhydride. This reaction can give the endo or the exo product. This reaction is kinetically controlled and mainly gives the endo product. Therefore, the exo transition state should be higher in energy; this will be examined by finding the two transition states. The first step was to optimise the reactants. The transition state was then calculated by the freezing coordinate methods, and the results can be seen below. To ensure the structure found was a transition state, a frequency analysis was done, proving that there was only one imaginary frequency.

Transition state	Vibration Animation	Frequency (cm^-1)
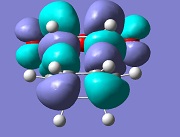
Exo		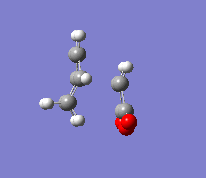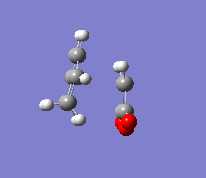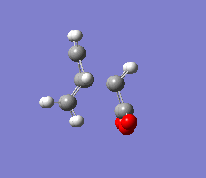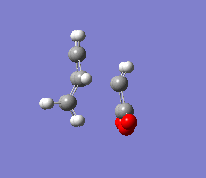-812
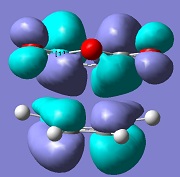
Endo		-806

The energy of the endo transition state was -0.050503 a.u. while the exo transition state's energy was -0.051594 a.u. This supports the fact that the reaction mainly gives the endo product, as the activation energy is lower. The exo form has a higher energy due to the higher strain energy involved. The angle between the C=C bond breaking and the lower fragment is of 96.7° for the endo transition state while it is 92.8° for the exo one. The endo angle is clearly closer to 109°, the ideal angle in an sp³ hybridised atom. This will reduce the energy. The partially formed bond lengths are 2.16 A for the endo product and 2.17 A for the exo product, which are fairly similar values.

The two transition states can be seen below.

9B

The molecular orbital analysis of both transition states shows that the LUMO and the HOMO of both structures are anti-symmetric. By examining the molecular orbitals, one can see a secondary orbital overlap effect in the endo structure, between the π* C=O orbital and the conjugated system in cyclohexadiene. This is only possible in the endo structure, because in the exo structure, the maleic anhydride points in the other direction and is therefore too far away to interact. This helps stabilise the endo product further, explaining why this is the major product.

	HOMO	LUMO
Exo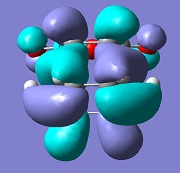
Endo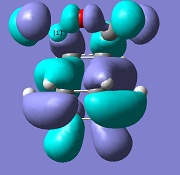

Conclusion

In conclusion, one can say that transition states can be well characterised by using computational techniques. A good agreement with experimental results can be achieved without too much computational effort, and this can help us rationalise and predict certain reaction mechanisms and their products. However, one has to be aware of the limits of the methods. For more accurate results, a higher level of precision is required, which will increase computational time. Computational techniques cannot tell us whether a reaction is driven by kinetic or thermodynamic control. Finally, one has to take into account that only one molecule is examined during the analysis, while in reality, there are many different particles interacting.

References

↑ B.W. Gung, Z. Zhu and R. A. Fouch, J. Am. Chem. SOC. 1995,117, 1783-1788; DOI:10.1021/ja00111a016
↑ O. Wiest, K. A. Black and K. N. Houk, J. Am. Chem. SOC., 1994,116, 10336-10337; DOI:10.1021/ja00101a078
↑ L. S. Bartell, J. Am. Chem. Soc., 1959, 81 (14); DOI:10.1021/ja01523a002
↑ B. P. Stoicheff, Tetrahedron letters, 1962, 17 (3/4); DOI:10.1016/S0040-4020(01)99013-1

[1] B.W. Gung, Z. Zhu and R. A. Fouch, J. Am. Chem. SOC. 1995,117, 1783-1788; DOI:10.1021/ja00111a016

[2] O. Wiest, K. A. Black and K. N. Houk, J. Am. Chem. SOC., 1994,116, 10336-10337; DOI:10.1021/ja00101a078

[3] L. S. Bartell, J. Am. Chem. Soc., 1959, 81 (14); DOI:10.1021/ja01523a002

[4] B. P. Stoicheff, Tetrahedron letters, 1962, 17 (3/4); DOI:10.1016/S0040-4020(01)99013-1

[1]

[2]

[3]

[4]