Rep:Mod:mod2 JB
Jessica Bevan: Computational Lab, Module 2
Introduction
Computational Chemistry has a vast array of uses in Inorganic Chemistry. Recently is has been used to further understanding of the reactivity of molecules; especially transition metals. [1] Improvements in computational chemistry have lead to Ab initio and density functional calculations being performed on a routine basis by non specialists in the field. [2] The following calculations were performed using Gaussian 09W, and Gauss View was used to analyse Virbrations, Molecular Orbitals, Bond lengths and angles.
BH3
Introduction
BH3 was modelled with a trigonal planar geometry, in Gauss View and the B-H bond length set to 1.5Ao. Calculations were then performed to obtain an optimised geometry, IR spectra, NBO and MO analysis.
Geometry Optimisation
| BH3 Optimisation | |
|---|---|
| File Name | BH3 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.46226338 a.u. |
| RMS Gradient Norm | 0.00020672 a.u. |
| Imaginary Freq | - |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3h |
| Job cpu time | 3 minutes 14.0 seconds |
| B-H Bond Length | 1.19349 Ao |
| H-B-H Bond Angle | 120 o |
| File | https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:BH3_optimised_JB.out |
The B-H bond length is in good agreement with the literature of 1.1919Ao [3]. The bond angle H-B-H is also in excellent agreement with literature of 120. [4]
Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES Predicted change in Energy=-1.071764D-06 Optimization completed. -- Stationary point found.
The geometry was only fully optimised after 4 iterations. These iterations are displayed below, with the intermediate geometries next to their appropriate stage on the graph. The final geometry is said to be fully optimised as the RMS gradient is close to 0.


Although a stationary point has been confirmed, vibrational analysis will be used to decide if it is a maximum or minimum. If all vibrations are poisitive a minimum energy will have been found.
Vibrational Analysis
Vibrational analysis was performed using the same method and basis set as the optimisation, and the result is displayed below along with the output file.
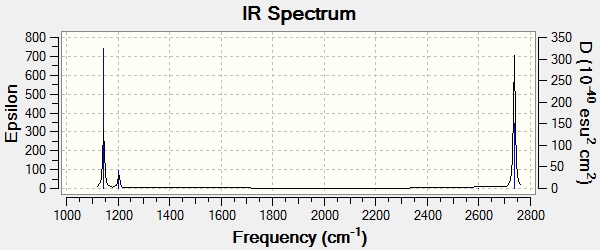
The graph only displays three peaks, but 6 vibrations are present. This is because two vibrations are degenerate meaning that only one peak for each is seen. The A' vibration is totally symmetric which means that there is no overall change in dipole so the stretch is not observed. BH3 has a point group of D3h. Each vibration is displayed below along with their allocated point groups. All vibrations are poisitive showing that the above optimisation was a minimum.
| Vibration | Animation for 1144.15 |  |
 |
 |
 |
 |
| Frequency | 1144 | 1204 | 1204 | 2598 | 2737 | 2737 |
| Literature Frequency [5]
|
1125 | 1604 | 1604 | 2623 | 2808 | 2808 |
| % Difference in Frequency | 2 | 33 | 33 | 1 | 3 | 3 |
| Intensity | 93 | 12 | 12 | 0 | 104 | 104 |
| Point Group | A"2 | E' | E' | A'1 | E' | E' |
| Vibration Mode | Out of Plane Wagging | In Plane Scissor | In Plane Rocking | Symmetric Stretch | Asymmetric Stretch | Asymmetric Stretch |
Overall, the frequencies are in good agreement with literature. The standard margin of error is known to be around 8%, the only peak to exceed this is E' 1204, which is 33% different from literature. This value is far from literature, and can only be explained by assuming the molecule perhaps isnt fully optimised.
Molecular Orbitals
Molecular Orbitals were computed using DFT-B3LYP method and a basis set of 3-21G, and the result is displayed on the MO diagram below. Full NBO analysis was also computed in the same calculation.

The LCAO method was used to construct the diagram, and it has a good fit to the computationally calculated orbitals. The MO shows that the 3a2' is above the 2e', which can only be discovered computationally.
Natural Bonding Orbitals
The natural charge of each atom was calculated at the same time as the MO.

Above is a diagram allocating the charges to the appropriate atom. As you can see, the hydrogens all have the same charge, proving the high symmetry of the molecule. The boron is electro positive and the hydrogens electronegative. This can be explained by considering that boron has an empty p orbital that can accept electrons [6].
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.27816 1.99954 2.72230 0.00000 4.72184
H 2 -0.09272 0.00000 1.09256 0.00015 1.09272
H 3 -0.09272 0.00000 1.09256 0.00015 1.09272
H 4 -0.09272 0.00000 1.09256 0.00015 1.09272
=======================================================================
* Total * 0.00000 1.99954 6.00000 0.00046 8.00000
The above table summerises the natural population and their contributions to the total charge.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99854) BD ( 1) B 1 - H 2
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 2 s(100.00%)
1.0000 0.0001
2. (1.99854) BD ( 1) B 1 - H 3
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 3 s(100.00%)
1.0000 0.0001
3. (1.99854) BD ( 1) B 1 - H 4
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.00%)p 1.00(100.00%)
10. (0.00015) RY*( 1) H 2 s(100.00%)
-0.0001 1.0000
11. (0.00015) RY*( 1) H 3 s(100.00%)
-0.0001 1.0000
12. (0.00015) RY*( 1) H 4 s(100.00%)
-0.0001 1.0000
13. (0.00146) BD*( 1) B 1 - H 2
( 54.64%) 0.7392* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 45.36%) -0.6735* H 2 s(100.00%)
1.0000 0.0001
14. (0.00146) BD*( 1) B 1 - H 3
( 54.64%) 0.7392* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 45.36%) -0.6735* H 3 s(100.00%)
1.0000 0.0001
15. (0.00146) BD*( 1) B 1 - H 4
( 54.64%) 0.7392* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 45.36%) -0.6735* H 4 s(100.00%)
1.0000 0.0001
The bonding in terms of hybridisation is displayed in the above table. The first three results describe natural bonding orbitals between hydrogen and boron. They each show a contribution of boron at 45.36% and they have 33.33% s and 66.67% p character. The contirbution from hydrogen is completely s in character. The core has 100% s character, as does the boron lone pair10-12 RY* are soley from hydrogen and have 100% s character. 13-15 are anti bonding orbitals that each show a contribution from boron of 54.64% which is made up of 33.33% p and 66.67% s character. The hydrogen contribution is totally s in nature.
"Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis" outlines mixing of molecular orbitals. However mixing is not significant in BH3 and therefore not alot of information is shown (below).
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1 4. CR ( 1) B 1 / 10. RY*( 1) H 2 0.70 7.42 0.064 4. CR ( 1) B 1 / 11. RY*( 1) H 3 0.70 7.42 0.064 4. CR ( 1) B 1 / 12. RY*( 1) H 4 0.70 7.42 0.064
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99854 -0.43328
2. BD ( 1) B 1 - H 3 1.99854 -0.43328
3. BD ( 1) B 1 - H 4 1.99854 -0.43328
4. CR ( 1) B 1 1.99954 -6.68393 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.53915
6. RY*( 1) B 1 0.00000 0.37512
7. RY*( 2) B 1 0.00000 0.37512
8. RY*( 3) B 1 0.00000 -0.04064
9. RY*( 4) B 1 0.00000 0.41499
10. RY*( 1) H 2 0.00015 0.73308
11. RY*( 1) H 3 0.00015 0.73308
12. RY*( 1) H 4 0.00015 0.73308
13. BD*( 1) B 1 - H 2 0.00146 0.42130
14. BD*( 1) B 1 - H 3 0.00146 0.42130
15. BD*( 1) B 1 - H 4 0.00146 0.42130
-------------------------------
Total Lewis 7.99516 ( 99.9396%)
Valence non-Lewis 0.00437 ( 0.0547%)
Rydberg non-Lewis 0.00046 ( 0.0058%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
TlBr3
Introduction
A molecule of TlBr3 was drawn in Gauss View and its symmetry set to D3h with very tight tolerance. An optimisation was then performed with a method of DFT-B3LYP and basis set of LanL2DZ. This method and basis set were also used for vibrational analysis otherwise the optimisation of the molecule may change and then the calculations are not valid. Frequency analysis was performed to ensure that the optimisation is a minimum as apposed to a maximum. So long as all the virbations calculated are positive, the molcule has reached a minimum energy point.
Geometry Optimisation
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:TLBR3_OPTIMISATION2_JB.LOG
| TlBr3 optimisation | |
|---|---|
| File Name | TlBr3_optimisation2 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -125.65149402 a.u. |
| RMS Gradient Norm | 0.00810128 a.u. |
| Imaginary Freq | - |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3h |
| Job cpu time | 43.0 seconds |
| Tl-Br Bond Length | 2.62160 Ao |
| Br-Tl-Br Bond Angle | 120 o |
Tl - Br bond length agrees well with the literature of 2.52Ao [7]
Vibrational Analysis
Vibrational analysis was performed using the same basis and method as for optimisation. The low frequencies are displayed below:
Low frequencies --- -9.7739 -0.0603 -0.0253 0.0036 10.3610 10.3612 Low frequencies --- 39.2801 39.2834 55.4951
The first row are the vibrations at the centre of mass of the molecule. The highest zero frquency is 10cm-1 and the first vibration is 39cm-1 which is 4 times as big as the zero frequency. The zero frequencies are very close to 0, which indicates that the method used is good.
| Mode # | 3 | 2 | 1 | 4 | 6 | 5 |
| Frequency | 55.50 | 39.28 | 39.28 | 271.34 | 313.80 | 313.80 |
| Intensity | 10.42 | 0.90 | 0.90 | 0.00 | 25.54 | 25.55 |
| Point Group | A"2 | E' | E' | A'1 | E' | E' |
| Vibration Mode | Out of Plane Wagging | In Plane Scissor | In Plane Rocking | Symmetric Stretch | Asymmetric Stretch | Asymmetric Stretch |
TlBr3 frequency DOI:10042/to-11913 It should be noted that Gauss View does not show any bonds in the molecule as it has defined distances for bond length, and is unable to consider distortions from the norm. A chemical bond is the sharing of electrons between two atoms.[8] Thus, whether gaussview pictorially represents the bond or not, there is still a bond there.
Cis Trans Isomerisation
Introduction
The following section analyses the difference between a cis and trans Molybdenum complex in the form of ML2X4. The original molecule to be studied was M(CO)4(PPh3)2 but due to the complexity of the PPh3 ligand it will be replaced with Cl. As Cl and PPh3 have a similar electronic contribution they should produce very similar vibrational spectra.
Through optimising the geometries of the cis and trans complexes, and computing their vibrational spectra, it will be possible to show the spectral differences between the two compounds.
Optimisation
The molecules were optimised using 3 different basis sets. The first time using LanL2MB, the second using LanL2DZ and lastly using seperate pseudo potentials for Mo and Cl, C and O. Mo is a heavy atom and therefore needs to be treated differently, using LanL2DZ. The Cl, C and O are treated using 6-331G (d,p).
| File Name | Cis opt 1 | Cis opt 2 | Cis opt New Basis | Trans opt 1 | Trans opt 2 | Trans opt New Basis |
| File Type | .log | .log | .log | .log | .log | .log |
| Calculation Type | FOPT | FOPT | FOPT | FOPT | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | LANL2MB | LANL2DZ | GEN | LANL2MB | LANL2DZ | GEN |
| Charge | 0 | 0 | 0 | 0 | 0 | 0 |
| Spin | Singlet | Singlet | Singlet | Singlet | Singlet | Singlet |
| E(RB3LYP) (a.u.) | -617.52501693 | -623.57707195 | -623.69291204 | -617.52205089 | -623.57603101 | -623.69415604 |
| RMS Gradient Norm (a.u.) | 0.00011115 | 0.00000392 | 0.00005593 | 0.00006227 | 0.00001253 | 0.00000642 |
| Imaginary Freq | - | - | - | - | - | - |
| Dipole Moment (Debye) | 8.4617 | 1.3107 | 0.0712 | 0.0000 | 0.3048 | 0.2294 |
| Point Group | C1 | C1 | C1 | C1 | C1 | C1 |
| Job cpu time | 11 minutes 59.5 seconds | 1 hours 11 minutes 53.7 seconds | 31 minutes 54.1 seconds | 4 minutes 49.7 seconds | 46 minutes 8.6 seconds | 42 minutes 3.4 seconds |
| DOI:10042/to-11910 | DOI:10042/to-11912 | DOI:10042/to-11915 | DOI:10042/to-11911 | DOI:10042/to-11909 | DOI:10042/to-11914 |
There is no significant difference between the different basis sets, although the last set, which seperates the atoms, should be the most accurate. Comparing between cis and trans in the same basis set, you can see that they are of very similar energies. All energies are in hartrees, and on conversion to kj/mol, it can be said that the trans is more stable by 5.251kj/mol. This can be explained by considering the sterics of the molecule. The more bulky groups will want to be as far as possible from eachother, thus trans.
If the R group in PR3 ligand interacted favourably with one cis to it, then the cis form would become more favourable. For example, if it contained hydrogen bonding groups such as -OH or NH2 then this would be a favourable conformer.
Vibrational Analysis
Vibrational analysis was carried out to ensure the optimised geometries were minimums. The basis set method used was to seperate the atoms, as for the best optimisation. Vibrational analysis is also the only way to find the difference between the two isomers as the C=O vibrations are different.
The overall point group of Cis is C2V.

The overall point group of trans is D4h.
| Vibration |  |
 |
 |
 |
 |
| Computational Frequency | 275.91 | 1939.19 | 1939.90 | 1966.85 | 2025.50 |
| Intensity | 0.04 | 1605.62 | 1606.02 | 5.89 | 5.40 |
| Point Group | A1g | Eu | Eu | B1g | A1g |

| File Name | cis_frequency2 | trans_frequency2 |
| File Type | .fch | .fch |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | GEN | GEN |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| Total Energy | -623.69291204 | -623.69415604 |
| RMS Gradient Norm (a.u.) | 0.00005608 | 0.00000641 |
| Imaginary Freq | - | - |
| Dipole Moment (Debye) | 0.0712 | 0.2293 |
| DOI:10042/to-11905 | DOI:10042/to-11904 |
Dimers of Gallium
Introduction
Gallium is a heavy post transition metal and is not present as an element in nature. It is used frequently in semi conductors as Gallium arsenide, and LEDs. Gallium 67 is used in medicine to treat cancer as it is able to locate malignant tissue and damage it without harming the surrounding healthy tissue. [9]
The aim of this project is to consider how Gallium dimers containing differing amounts of Chlorine ligands differ in energy and conformation. The Cis and Trans form of Ga2Cl4H2 will be considered, and the most stable form of the Gallium dimer found. Then Ga2Cl2H4, Ga2Cl4H2 and Ga2Cl6 will be analysed to look at the effected of increasing the Cl substituents on Gallium.
Changing Dimer Substituents
The following picture illustrates the molecules to be examined along with the names allocated to allow easy labbeling:
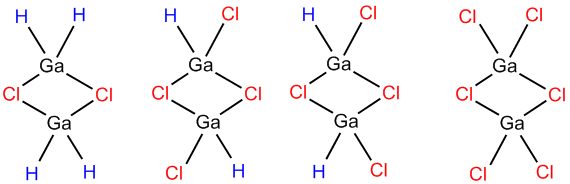
Optimisation
All four molecules were optimsed using the RB3LYP method and LANL2DZ basis set, then they were optimised using the same method but with a basis set of GEN and the word pad edited so that Gaussian was instructed to apply LANL2DZ basis set to the Ga atom and 6-331G (d,p) to the C and H atoms because Ga is a heavy atom.
| Molecule | 2Cl | Cis | Trans | All Cl | ||||
| File Type | .log | .log | .log | .log | .log | .log | .log | .log |
| Calculation Type | FOPT | FOPT | FOPT | FOPT | FOPT | FOPT | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | GEN | LANL2DZ | GEN | LANL2DZ | GEN | LANL2DZ | Gen |
| Charge | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Spin | Singlet | Singlet | Singlet | Singlet | Singlet | Singlet | Singlet | Singlet |
| E(RB3LYP) (a.u.) | -36.52630343 | -927.08452102 | -65.33910751 | -1846.44617988 | -65.33973404 | -1846.44687623 | -94.13779388 | -2765.79134950 |
| RMS Gradient Norm (a.u.) | 0.00000191 | 0.00001558 | 0.00000929 | 0.00000323 | 0.00001218 | 0.00000319 | 0.00001958 | 0.00002184 |
| Imaginary Freq | - | - | - | - | - | - | - | - |
| Dipole Moment (Debye) | 0.0006 | 0.0016 | 4.0473 | 3.5620 | 0.0020 | 0.0014 | 0.0050 | 0.0052 |
| Point Group | C2V | C2V | C2V | C2V | CS | CS | C2V | C2V |
| Converged? | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Predicted Energy Change | -7.148962D-10 | -2.999457D-08 | -2.567520D-08 | -2.115499D-09 | 1.653610D-08 | -8.682387D-10 | -3.771007D-08 | -2.496057D-08 |
| DOI link | DOI:10042/to-11928 | DOI:10042/to-12163 | DOI:10042/to-12129 | DOI:10042/to-12141 | DOI:10042/to-12130 | DOI:10042/to-12142 | DOI:10042/to-11930 | DOI:10042/to-12164 |
According to literature, the Trans isomer is more stable than the Cis [10]. Looking at the energies calculated, they seem to be nearly identical in energy for both basis sets. Using the LanL2DZ it can be seen that Trans is stable by 0.0006 a.u. and the GEN basis set gives Trans to be more stable by 0.0007 a.u., agreeeing with literature.
Looking at the trend between all 4 molecules, it can be said that adding 2Cl atoms to the molecule increases the energy. There is a very clear trend that is displayed in graphs below:
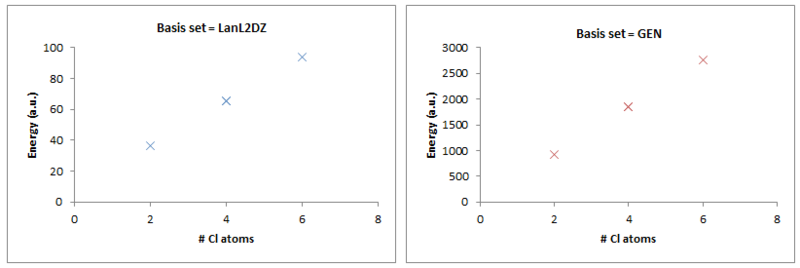
As you can see, the energy of the molecule increases linearly with the # of Chlorine atoms present in the dimer.
Below is a comparison of calculated bond lengths and angles to literature [11] [12] :
| Molecule | 2Cl(B) | trans | cis | All Cl |
| Bond Length Ga-Cl(B) | 2.46891 | 2.44628 | 2.44705 | 2.42671 |
| Literature | 2.3493 | 2.386 | 2.386 | 2.300 |
| Bond Length Ga-Cl(T) | - | 2.1973 | 2.19419 | 2.17751 |
| Literature | - | 2.149 | 2.145 | 2.099 |
| Bond Angle Ga-Cl(B)-Ga | 93.837 | 94.086 | 94.189 | 93.458 |
| Literature | 87.28 | 92.1 | 92.2 | 91.74 |
| Bond Angle X-Ga-Y | 134.820 | 126.696 | 126.615 | 123.407 |
| Literature | 120.0 | 126.4 | 126.6 | 125.1 |
Key: Cl(B) = Bridging Cl atom Cl(T) = Terminal Cl atom X-Ga-Y = Angle between terminal substituents
Looking at the table displaying bond lengths and angles the foloowing points can be outlined:
- All Trans and Cis bonds and angles are practically identical to each other
- Computational gives higher values than experimental.
- The Ga-Cl(B)computational values decreases by 0.02 on each addition of 2 Cl atoms
- The literature values for Ga-Cl(B)do not follow the same trend, instead the Trans and Cis isomers have the highest value, leading to no real trend, and poor correlation between literature and computational values
- The bond length Ga-Cl(T) decreases from Trans/Cis to All Cl, agreeeing with literature
- Bond Angle Ga-Cl(B)-Ga for 2Cl is not very close to literature, and there is no real trend between dimers
- Bond Angle X-Ga-Y gives a nice trend for computational trends, but literature shows no trend, therefore its unlikely that the trend exists, and is more likely down to a chance computational error
IR
The frequencies for all 4 molecules were calculated, and no value was negative, verifying that the geometries were minimums. The main uniques peaks are outlined below:
| Molecule | Frequency | Intensity | Type |
| 2Cl | 1991.37 | 278.5951 | H+Cl symm asymm stretching |
| 2Cl | 1989.17 | 0.0000 | H+Cl asymm asymm stretching |
| 2Cl | 1971.99 | 0.0000 | H+Cl symm symm stretch |
| 2Cl | 1969.34 | 110.6275 | H+Cl asymm symm stretch |
| Trans | 578.58 | 305.9051 | in plane H sub>wagging |
| Cis | 578.13 | 240.0078 | in plane H wagging |
| Trans | 534.66 | 171.9435 | out of plane H wagging |
| Cis | 535.30 | 171.2535 | out of plane H wagging |
| Trans | 2019.14 | 102.6500 | H-_H symm stretch |
| Cis | 2016.40 | 74.2274 | H-_-H symm stretch |
| Trans | 2019.33 | 102.6500 | H-_H asymm stretch |
| Cis | 2014.80 | 43.5385 | H-_-H asymm stretch |
| Trans | 389.54 | 0.0009 | symm Cl-_Cl stretch |
| Cis | 394.84 | 54.0653 | Symm Cl-_-Cl stretch |
| Trans | 387.03 | 104.4812 | asymm Cl-_Cl stretch |
| Cis | 385.48 | 45.0194 | asymm Cl-_-Cl stretch |
| All Cl | 437.95 | 115.1462 | 2Cl(T) symm Antisymmetrical stretching |
| All Cl | 432.34 | 0.0000 | 2Cl(T) asymm Antisymmetrical stretching |
| All Cl | 375.20 | 0.0000 | 2Cl(T) symm Symm stretch |
| All Cl | 359.55 | 108.1252 | 2Cl(T) asymm symm stretch |
As expected, Trans and Cis are very similar, differing by a few cm-1
 |
 |
 |
 |
Further IR analysis for 2Cl
| Symmetry | expt | Comp | % Difference | Type |
| ag | 1990 | 1972 | 1 | Ga-H stretch |
| ag | 120 | 168 | 40 | Ring def. |
| b2g | 2020 | 1991 | 1 | Ga-H stretch |
| b1u | 2020 | 1989 | 2 | Ga-H stretch |
| b3u | 1985 | 1969 | 1 | Ga-H stretch |
Overall the computed values agree with the experimental values in the order of +/- 1%, but there is a huge difference for the ag ring def. vibration. This could be due to missasignment or because the optimisation simply was not good enough.
NBO
 |
 |
 |
 |
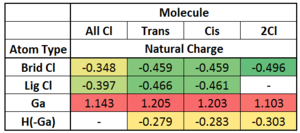
The above table shows that the Ga atom is all cases stays electro positive and is the most positive in the Trans/ Cis dimer. There is a steady trend of increasing electronegativity of the bridging Cls with decreasing number of Cl substituents. The Cl atoms are more negative than the H reflecting their relative electronegativities. The terminal Cl are more negative than their bridging partners, possibly due to the fact that the bridging bond is not a full bond but is 3c-2e in nature. In the All Cl dimer, the Ga is more deshielded compared to the other dimers because it is bonded to 4 Chlorines, however the natural charge does not reflect this, as it would be expected to have a higher positive charge, but is lower than the Cis/Trans Ga.
MO
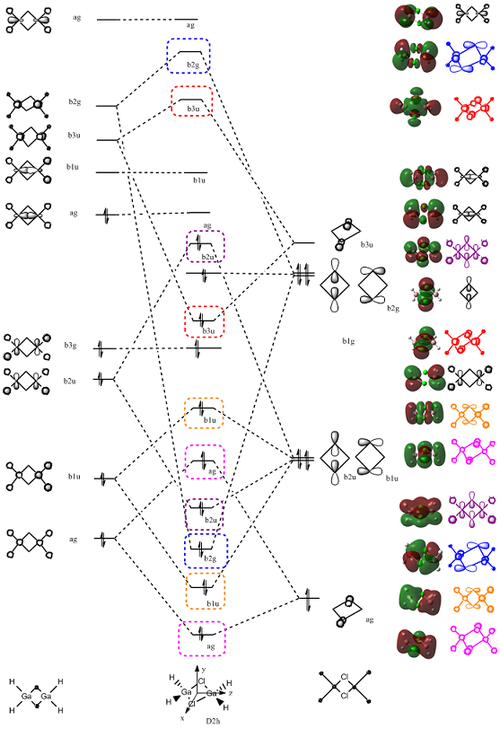
MOs were calculated using the same method and basis set as frequency, but submitted for energy calculations. The following diagram illustrates the MO energy diagrams of each dimer:
As you can see, all of the LUMOs lie below the 0 energy line and are non bonding. The MOs of cis and trans are identical in energy, but differ in geometry (see diagrams below). The HOMO/ LUMO is more stable on increasing the Cl substituents, with All Cl having the lowest energy HOMO and the most bonding orbitals. This is because the Cls contribute 3 p orbitals for bonding, whereas H only conjtributes 1 s, this means that there are far more favourable interactions possible in All Cl than any of the other dimers.
| All Cl |  |
 |
| Cis |  |
 |
| Trans |  |
 |
| 2Cl |  |
 |
Looking at the above diagrams, it can be seen that the Cis and Trans both have the same HOMO and LUMO, but different symmetries. Both cis and trans's LUMOs have diffused Ga orbitals. The HOMO and LUMO of All Cl are totally symmetric, as expected, with the HOMO being comprised totally of Cl p orbitals and the LUMO again contains very diffused Ga orbtials. The HOMO of 2Cl comprises of H s orbitals and 2 p orbitals from the 2 Cls. Its LUMO is made up of very diffused Ga orbitals. The MO of 2Cl is analysed in great detail below.
The following is a diagram showing how the initial GaH2 fragment was produced:

The following is a diagram showing how the GaH2 fragment became a Ga2H4 fragment:

This is the final MO of 2Cl:
As you can see from the final MO, the LCAO method of predicting molecular orbitals has been very accurate and the predicted orbitals are very close in shape to those computed. The computed MOs helped to decide the energies of each orbital, and thus the final diagram was produced.
References
- ↑ Andreja Bakac, Physical inorganic chemistry: principles, methods, and models
- ↑ John P. Fackler, Jr, Techniques in Inorganic Chemistry
- ↑ Cheuk-Yiu Ng, Vacuum ultraviolet photoionization and photodissociation of molecules and clusters, p29
- ↑ William H. Brown, Christopher S. Foote, Brent L. Iverson, Organic Chemistry, p237
- ↑ Kaldor, A.; Porter, R.F., J. Am. Chem. Soc., 1971, 93, 2140
- ↑ Tony D. James, Marcus D. Phillips, Seiji Shinkai, Boronic acids in saccharide recognition, 2006
- ↑ Johan Blixt Julius Glaser, J Jhos Minks Ingmar Persson, Per Perssond and Magnus Sandstr, Structure of Thallium(II1) Chloride, Bromide, and Cyanide Complexes in Aqueous Solution, J. Am. Chem. Soc. 1995, 117, 5089-5104
- ↑ E. Ramanathan M.Sc., M.Phil., B.Ed., Dictionary of Chemistry, 2005
- ↑ Robert E. Krebs, The history and use of our earth's chemical elements: a reference guide, 2006
- ↑ Gilbert J. Mains, Charles W. Bock, Mendel Trachtmanc, Vladimir S. Mastryukovd, Journal of Molecular Structure, Volume 274, 1992
- ↑ B.J. Duke, T.P. Hamilton and H.F. Schaefer III, Inorg. Chem., 30(1991) 4225
- ↑ M.M. Akobiya, V.I Bregadze, L.M. Golubinskaya, Journal of Organometallic Chemistry Volume 467, Issue 2, 1994