Rep:Mod:mod1ii108
Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations
Irene Iriarte Carretero, October 2010
Introduction
This page will deal with the modelling of several aspects of organic structure and reactivity, in order to be able to provide explanations for certain behaviours or to predict the outcome of reactions. The strengths and weaknesses of certain techniques will be analysed. The first method used will be Molecular Mechanics, which works by optimising molecular geometries until a minimum energy is reached. However, this approach uses previously known data and therefore cannot be used when dealing with molecules or reactions that differ from this. It does not take into account transition state or quantum mechanics, which makes it a weak method when dealing with stereoelectronic effects or molecular orbitals, for example. In the second part of this page, a Semi-Empirical Molecular Orbital Theory will be used, which will be more accurate in a lot of respects, as it handles the quantum mechanical approach, explicitly taking into account electrons in molecules and how they influence bonds and reactions.
Modelling using Molecular Mechanics
The Hydrogenation of Cyclopentadiene Dimer
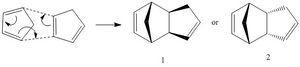
Cyclopentadiene undergoes a [4π+2π] Diels-Alder reaction in order to produce a cyclopentadiene dimer. Diels-Alder reactions can produce two different products: the endo (molecule 2) and the exo product (molecule 1). The energies of the two products were analysed through the use of Molecular Dynamics (MM2) and the results revealed that the endo product had an energy of 34.0153 kcal/mol while the energy of the exo product was found to be 31.8782 kcal/mol. This means that the exo product is the less strained of the two. However, it is the endo product that is formed during the reaction, which suggests that the reaction is in fact kinetically controlled.
| Energy (kcal/mol) | Molecule 3 | Molecule 4 |
|---|---|---|
| Stretch | 1.2659 | 1.0963 |
| Bend | 19.8063 | 14.5075 |
| Stretch-Bend | -0.8276 | -0.5493 |
| Torsion | 10.8698 | 12.4972 |
| Non-1,4 VDW | -1.2207 | -1.0507 |
| 1,4 VDW | 5.6394 | 4.5124 |
| Dipole/Dipole | 0.1621 | 0.1407 |
| Total | 35.6953 | 31.1540 |
This can be explained by analysing the frontier orbitals of the two cyclopentadienes as they react. One can see that not only is the symmetry correct in order to form the bond, but there are also additional bonding interactions at the back of the diene. The endo product is therefore favoured. [1]

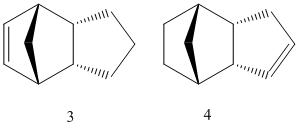
This cyclopentadiene dimer can then be hydrogenated to give a dihydro derivative, needing a long reaction time to get to the tetrahydro molecule. Molecule 3 was found to have an energy of 35.6953 kcal/mol while molecule 4’s energy was significantly lower at 31.1540 kcal/mol. Molecule 4 would therefore be the predicted thermodynamic product of the reaction.
One can rationalise this by analysing the relative contributions from the different energy terms. The main difference between the two derivatives is caused by the bend energy (difference of more than 4 kcal/mol). The hydrogenation of the double bond adjacent to the strained bridge improves the bend energy more than the hydrogenation of the other double bond. This is because the double bond on the norborene unit causes a higher strain in the ring, due to the methylene bridging unit, than the double bond on the cyclopentene. The double bond on the norborene can therefore be hydrogenated more easily, leading to molecule 4 as the first product. This can be further proved by analysing the angles present at the sp2 carbons in both molecules. In the more favourable molecule 4, the angles between the two sp2 carbons and a neighbouring atom are of approximately 112°, while for molecule 3 the angles are 107°, clearly further away from the ideal 120°.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
This section analyses the stereochemistry of nucleophilic additions to a pyridinium ring, unit present in nicotinamide adenine dinucleotide (NAD+).
| Dihedral angle (°) | Energy of molecule (kcal/mol) |
|---|---|
| 11 | 43.1233 |
| 123 | 168.1987 |
| 13 | 44.5619 |
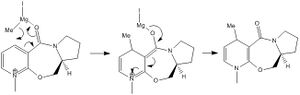
In the first reaction, a derivative of prolinol is reacted with methyl magnesium iodide in order to alkylate the pyridine ring at the 4-position. The mechanism can be seen below. This reaction is highly regio- and stereoselective, due to the high coordination between the Grignard reactions and the carbonyl oxygen, as proposed by Schultz and Flood [2]. This coordination then allows the conjugate delivery of the methyl group from the magnesium to the pyridinium ring. Through the use of Molecular Modelling (MM2), the optimum angle between the carbonyl group and the aromatic ring was calculated. This angle was 11°, which means that the MeMgI attacks from the top, therefore the alkylation occurs from the top as well, explaining the stereochemistry of the product. The geometry of the reagent was studied by optimising the energies and geometries of the reagents from different starting points. A table with several of these optimisations can be seen below. It shows that the lowest energy was achieved by having a dihedral angle of 11° and shows how certain conformations can be provided by the program which have an unrealistic energy values.
This model could have been improved by using a more precise technique that took into account things such as stereoelectronic effects and the effect that for example the magnesium would exert on the reacting molecule. A method which used a more quantic approach, taking into account molecular orbitals, would provide a more accurate result. In this example, Mg cannot be used in the calculations as ChemBio3D does not have the parameters needed to perform calculations with it.

The second reagent is reacted with aniline (PhNH2) to produce N-methylquinolinium (molecule 8). This reaction is also very regio- and stereoselective. The geometry was optimised, to find that the carbonyl is actually 20° below the plane of the ring. Therefore, attack of the aniline on the face below is sterically and electronically unfavourable, making sure that the attack is from the top, explaining the stereochemistry of the product shown. Attack from the bottom is sterically hindered due to the big phenyl group and electronically unfavourable because of the aniline nitrogen and the carbonyl oxygen lone pairs repulsion. The carbonyl therefore plays an important role in the high selectivity of the reaction[3]. Attempts at changing the molecule in order to find a different conformer were not succesful, as minimisation of geometry always gave the same result, with an energy of approximately 62.7 kcal/mol.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
| Energy (kcal/mol) | Molecule 9 | Molecule 10 |
|---|---|---|
| Stretch | 2.6451 | 2.5396 |
| Bend | 15.7683 | 10.6768 |
| Stretch-Bend | 0.3873 | 0.3239 |
| Torsion | 18.2525 | 19.6070 |
| Non-1,4 VDW | -0.9933 | -1.2130 |
| 1,4 VDW | 12.6839 | 12.5568 |
| Dipole/Dipole | 0.1465 | -0.1815 |
| Total MM2 | 48.8904 | 44.3096 |
| Total MMFF94 | 70.5436 | 60.5531 |
Atropisomers are stereoisomers that are formed through the hindered rotation about a single bond. In these cases, the conformers can be isolated because the steric strain barrier is very high. An example of this can be seen in an intermediate in the synthesis of taxol, as proposed by Paquette et al.[4] The carbonyl of the compound is either up or down, but when left to stand, the compound isomerises to the most stable isomer. In this section, the structures of both isomers were minimised and studied, in order to find the most optimum configuration. Force fields MM2 and MMFF94 were used to do this.

Several conclusions can be drawn from the table of energies shown below. The most stable structure is the optimised isomer 10, with the carbonyl pointing downwards. This can be explained by looking at the conformation of the rings in the molecules. In both cases, the five membered ring has the favourable twisted envelope. However, in the less stable isomer 9, the six membered ring exists in the higher energy twist boat conformation, rather than adopting the chair one. This is the case in the second isomer.
These isomers were found to react abnormally slowly and this is due to the fact that they are hyperstable alkenes. This sometimes occurs in bridgehead groups in medium sized ring systems.[5] This happens when the olefin has a negative olefin strain energy, lower than that of the parent hydrocarbon. Due to this low energy, these molecule's heat of hydrogenation are lower than normal and are therefore very slow to react, as they are very thermodynamically favoured.[6]
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Regioselectivity
The molecule 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene has been found to have very regiospecific reactions with electrophilic reagents such as dichlorocarbene or peracids. In order to study this property, a technique which analyses the geometry and molecular orbitals of the molecule was needed. This is more advanced than the previous method used, which relied purely on mechanics, rather than also taking into account the quantum approach.
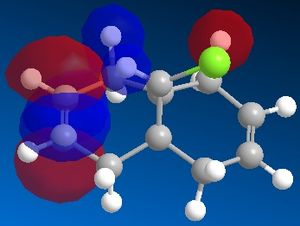
Therefore, the geometry was minimised using MM2 and then MOPAC/PM6 calculations were run to find a representation of the electron wavefunction. This produced pictorial representations of the molecular orbitals which can be seen below.
 |
 |
 |
 |
 |
The shape of these molecular orbitals can explain the reactivity. By observing the HOMO orbital, one can see much bigger electron density around the syn-alkene than around the anti-alkene. This means that electrophilic reagents will tend to attack the syn-alkene. However, under more extreme conditions, the anti-alkene can also react, as in the HOMO -1 one can see that it has significant electron density. Another reason is the antiperiplanar interaction between the C-Cl σ* orbital (LUMO +1) and the occupied exo π orbital (HOMO -1), which causes the exo orbital to be stabilised by approximately 0.08 eV with respect to the endo[7]
Vibrational analysis
In this part of this section, the vibrations of the molecule and of its derivatives are analysed. The table below shows the results.
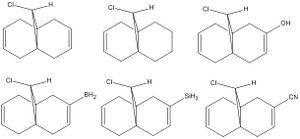
| Derivative | C-Cl | C=C (exo) | C=C (endo) |
|---|---|---|---|
| Di-alkene | 772.56 | 1740 | 1759 |
| Monoalkene (endo-alkene) | 774 | - | 1758 |
| Added -OH | 765 | 1753 | 1757 |
| Added -BH2 | 759 | 1657 | 1756 |
| Added -CN | 764 | 1706 | 1755 |
| Added -SiH3 | 764 | 1690 | 1756 |
The frequency for the C-Cl vibrations concur with the literature value of approximately 540-760 cm-1[8]. However, the C=C vibration frequencies are higher than the literature values of 1640–1680 cm-1[8]. This means that the bond is stronger than the average C=C bond and might occur because of the technique used to produce the spectrum, as it does not take many things into account.
In the di-alkene, one can see how the exo frequency is lower than that of the endo, which means that the exo-alkene has lower energy than the endo-alkene. This is, as explained before, not caused by π interactions; therefore it will be caused by σ interactions or by unfavourable interactions within the whole molecule. The table also shows that the removal of the exo alkene bond hardly affects the frequencies of the C-Cl and the endo C=C stretches.
Certain groups were added to the exoalkene in order to investigate the effect this had on the frequencies. The results show that the C-Cl and the endo C=C frequencies were almost unaffected. However, the exo C=C stretches clearly show changes. The BH2 group produces the lowest frequency and therefore the weakest bond. This could be because B has empty p-orbitals which can accept electron density from the double bond. Adding the cyano group also produces a weaker bond due to the higher electronegativity of the nitrogen with respect to the carbon, attracting electron density to itself. Finally, the silicon group also reduces the strength of the bond due to the empty d-orbitals. However, the hydroxy groups makes the bond stronger because of it can donate electron density into the bond through resonance.
Structure based Mini project using DFT-based Molecular orbital methods
The reaction investigated in this section is the ruthenium-catalyzed [2 + 2] cycloadditions of 2-substituted norbornenes[9] . This reaction produces a pair of regioisomers, which were distinguished through the NMR technique ofheteronuclear multiple bond coherence (HMBC). This project will try and establish whether the NMR spectrum calculated through the use of DFT-based Molecular Orbital methods could distinguish between the two regioisomers. In order to do this, an NMR spectrum for each molecule will be calculated and this will then be compared with the actual literature values. The picture below shows the possible cycloaddition mechanisms; image taken from DOI:10.1021/ol006397t [9]
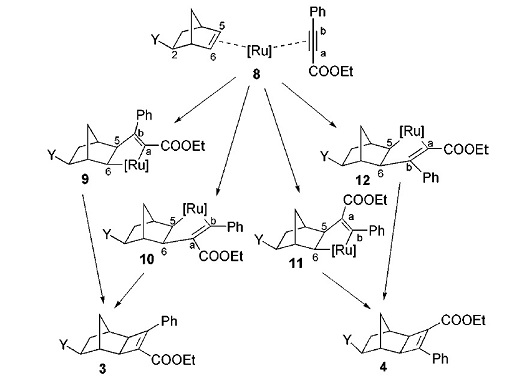
The reaction could potentially lead to four different cycloadducts, with two regioisomers for each the exo and endo cycloadducts. However, based on the work of Mitsudo et al. on Cp*RuCl-(COD)-catalyzed [2 + 2] cycloaddition of norbornene [10] where only the exo cycloadducts were formed, Jordan et al assumed that this would also be the case.
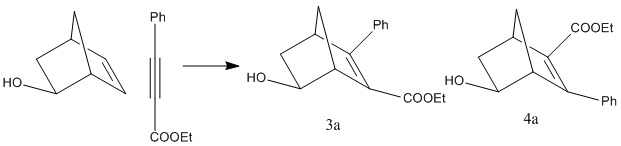
Therefore, the specific reaction scheme investigated can be seen below. OH was chosen as the electron withdrawing group Y in order to make the calculations easier, as the larger the groups the longer the computational time.
NMR Molecule 3a
The molecules were drawn on ChemBio3D and their energy minimised by first using MM2 and then MOPAC/AM1. This geometry was then sent to minimise further using DFT method mpw1pw91, which is more powerful than B3LYP used in the previous exercise. The basis set used was 6-31G(d,p). The completely minimised structure was then used to calculate the NMR chemical shifts. The results can be seen below.
|
|
The NMR calculated through DFT can be seen below.
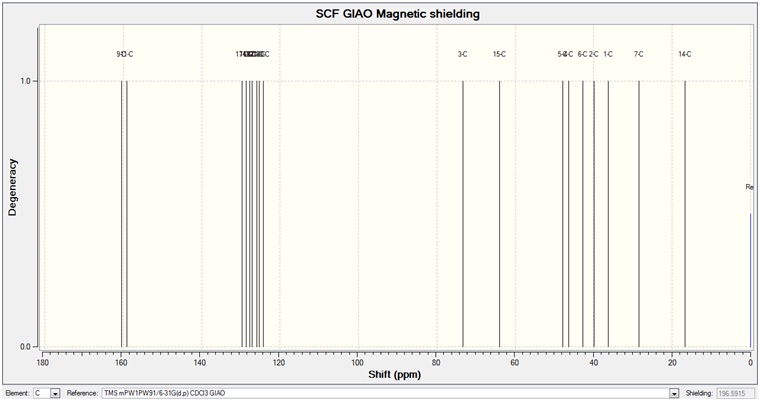
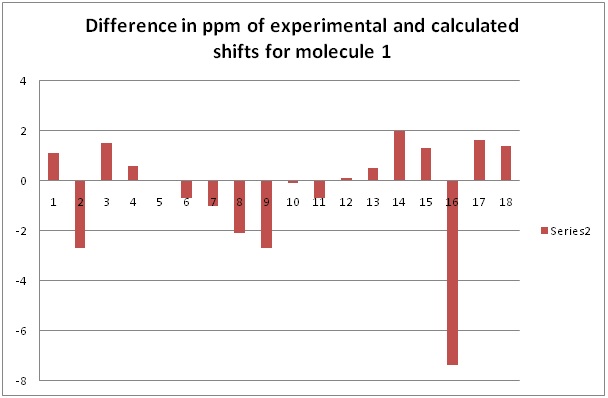
The graph below shows the differences between the calculated and the experimental values in ppm.

NMR molecule 4a
|
|
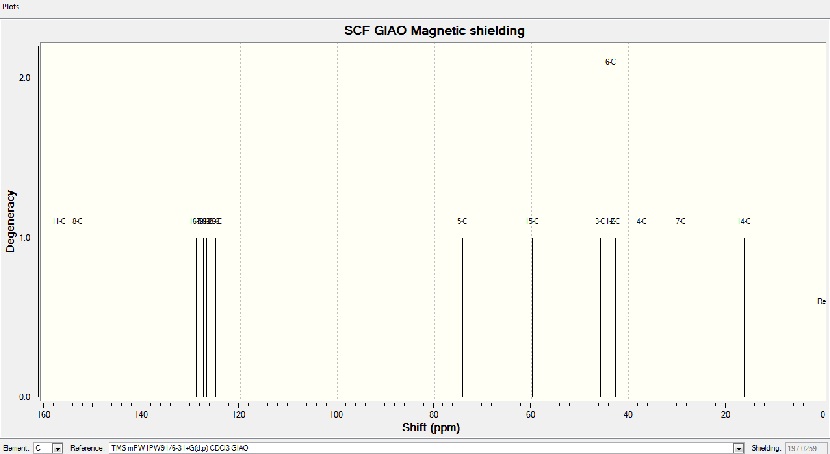
NMR analysis
In general, one can see how the predicted 13C NMRs are quite close to the actual values, apart from certain carbons, with the maximum difference being of about 7 ppm. The rest of the shifts seem to be within about 3 ppm, suggesting that the big difference of 7 ppm might be due to the basis set used. This information can be visualised in the graphs shown above, which show the difference between the calculated and the experimental NMR shift for each carbon atom as done in several journals.[11] The calculated values gave an individual shift for every carbon environment, while in the experimental values, the differences between the shifts were very small and therefore overlapped, showing a high degeneracy for a certain shift and therefore less peaks than in the calculated NMR. This mainly occurs in the phenyl ring.
However, it is clear that NMR is not a suitable method to distinguish between the two isomers, as they are very similar. In order to distinguish between them the NOE needs to be taken into account. NOE corresponds to the Nuclear Overhauser Effect and it is observed through space rather than through bonds. Jordan et al. use this to distinguish between the regioisomers by investigating the NOE between the different hydrogens. The hydrogens involved can be seen in the picture below[9].

Janocchio was used to find the NOE values for the hydrogens involved. The journal states that for regioisomer 3a, Ha should show an NOE effect with Hb, but not with Hc. However, for regioisomer 4a, Ha should show an NOE effect with Hc rather than Hb. Results with Janocchio indeed show that for molecule 3a, there is an NOE effect between Ha and Hb of 0.0322, while the one between Ha and Hc is 0.0019, which is significantly smaller. For molecule 3b, the interaction between Ha and Hc is 0.0337 while the interaction between Ha and Hb is 0.0021.
The coupling value between the hydrogens was used to determine that the cycloadducts formed were the exo adduct. The coupling between Hc and He in molecule 3a will be small (J =0-2 Hz) if the product is the exo adduct as the angle between the atoms would be approximately 90°. However, if the product was an endo adduct, the angle between the atoms would be around 40° and the coupling constant would be about 5Hz. The coupling constants were analysed with Janocchio as well and the result was that Hc and He show a coupling constant of 1.4 Hz which matches with the predictions.
Conclusion
In conclusion, one can say that molecular modelling is a very useful way of predicting and analysing reactions and molecules, if one is aware of the limitations that it entails. One must therefore be cautious when using the results obtained. In this particular example, molecular modelling was successful in identifying the different regioisomers, which means that the optimisation of the energy was correct and the methods then used to analyse it were also quite accurate. Different methods could also have been used, though they were not relevant in this example. One example of this is IR, which would not have helped distinguish between the two molecules. Another example is optical rotation which is irrelevant in this case.
References
- ↑ Clayden et al., Organic Chemistry, 1997, p916
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ # S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ # S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ # W. F. Maier and P. v R. Schleyer, J. Am. Chem. Soc., 1981, 103; DOI:10.1021/ja00398a003
- ↑ A. B. McEwen and P. v R. Schleyer, J. Am. Chem. Soc., 1986, 108; DOI:10.1021/ja00274a016
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ 8.0 8.1 IR Correlation Table[1]
- ↑ 9.0 9.1 9.2 R. W. Jordan and W. Tam, Organic Letters, 2000, 2 (19); DOI:10.1021/ol006397t
- ↑ T. Mitsudo, H. Naruse, T. Kondo, Y. Ozaki, Y. Watanabe, Angew. Chem., Int. Ed. Engl. 1994, 33
- ↑ C. Braddock and H. S. Rzepa, J. Nat. Prod., 2008, 71, 728-730. DOI:10.1021/np0705918
