Rep:Mod:mod1 jb
Introduction
Computational Chemistry, also known as Molecular Modelling is a set of procedures that enable the user to explore chemical problems on a computer.The usual aspects investigated are molecular geometry, the energy of the molecule and its transition state, and chemical reactivity. In addition, it allows the prediction of NMR, IR and UV spectra.
This is a very useful technique, especially if the compound being studied has not ever been synthesised, as the predicted spectra can be used to indicate if the molecule has been made. It is extensively used in the Pharmaceutical industry in order to investigate the interactions of drugs with biomolecules.Cite error: Invalid parameter in <ref> tag It is also used in order to complete the full picture of a molecule, as some properties are easier to model than obtain experimentally.[1]
The modelling methods used in this program are MM2, MOPAC-PM6, MOPAC-RM1, and Gaussian 09W exported into GaussView 05.
The MM2 method, developed by Scheleyer and Allinger in the 1960s, is based upon Newtonian physics. The MOPAC method uses the Hartree-Fock theory, which is based on molecular orbital theory. It averages the repulsions between electrons and is thus able to determine the conformation of molecules. Cite error: Invalid parameter in <ref> tag
Molecular Modelling
Introduction
Although plastic models can further our understanding of 3D effects, such as strain and steric hindrance, in reality, they are unable to compare two molecules quantitatively. One way to do this is to look at the summation of individual bond properties. This is the Molecular Mechanics approach, and it accounts for strain, steric repulsion and electrostatic interactions such as hydrogen bonding. In order to do this, the total energy of the molecule is minimised by adjusting bond lengths and angles.
This method only works well if the bonds in the molecule can be related to simple diatomic species. For more complex molecules, such as aromatic systems or charged species, the summation approach breaks down.
The MM model used in the chapter is MM2.
The Hydrogenation of Cyclopentadiene Dimer
The Reaction and Uses
Cyclopentadiene is found in the C5 fraction of naptha cracking, and is mainly used in the hydrocarbon resin industry and is a very important ligand used in catalysis due to its ability to change co ordination number from 1 3 or 5[2]. Dimerisation of cyclopentadiene occurs via a special case diels alder at 140- 150oC under pressure, producing the endo form, as seen in the below diagram.
Below is an outline of the mechanism:

The mechanism procedes via the classic Diels Alder reaction, and can produce either an endothermic product or an exothermic one. Looking at the above scheme, the product on the left, the endo product, is produced when the top cyclopentadiene approaches on top of the other. The product on the right (exo) is produced when the cyclopentadiene approaches on top, but at the side of the second cyclopentadiene. [3] [4]
This is better illustrated by looking at orbital overlap, and considering the effect of overlap, which will be discussed in the next section.
Endo Vs. Exo
In order to decide which product (1 or 2) is preferred computationally, we have to consider which one is the kinetic and which is the thermodynamic product, and the reaction conditions. Consulting the previously defined terms, the thermodynamic (exo) product is that with the lowest energy and the kinetic (endo) product is the one with the lowest energy transition state. Once the dimer is formed, it can then be hydrogenated to form dihydro derivatives, for example 3 and 4 are the dihydro derivatives of 2.
Using MM2 we can calculate the energies of all 4 products, and decide which is the more likely product.
Below is a table comparing the energies of the product (1) against product (2)
| ' | 1: Jmol for structure 1 | 2: Jmol for structure 2 |
| Stretch | 1.286 | 1.251 |
| Bend | 20.580 | 20.849 |
| Stretch - Bend | -0.838 | -0.8360 |
| Torsion | 7.655 | 9.511 |
| Non- 1,4 VDW | -1.416 | -1.544 |
| 1,4 VDW | 4.233 | 4.319 |
| Dipole Dipole | 0.378 | 0.448 |
| Total Energy (kcal/mol) | 31.877 | 33.998 |
The table shows that the product (1) is lower in energy by 2.121 kcal/mol, and is therefore the exo product. It is the most stable and will form when under thermodynamic control. The reaction is therefore under kinetic control in order that product (2) is the major product, and it therefore must have a lower energy transition state. This could be justified by considering orbital overlap on approach. The following diagram outlines the orbitals involved:

Looking at the above diagram, you can see that the endo approach involves more orbitals overlapping than the exo. This leads to an increase in the stabilisation of the bond formation, thus making the endo approach more stable.
The Hydrogenation of Endo Cyclopentadiene Dimer
On hydrogenation of the major (endo) product of cyclopentadiene dimerisation, two products can be obtained, depending on which alkene is hydrogenated. The MM2 method has been used to calculate the energies of each possible product and below is a table comparing those energies.
| 3: Jmol for structure 3 | 4: Jmol for structure 4 | |
| Stretch | 1.278 | 1.096 |
| Bend | 19.859 | 14.523 |
| Stretch - Bend | -0.835 | -0.549 |
| Torsion | 10.811 | 12.497 |
| Non- 1,4 VDW | -1.223 | -1.070 |
| 1,4 VDW | 5.633 | 4.514 |
| Dipole Dipole | 0.162 | 0.141 |
| Total Energy (kcal/mol) | 35.685 | 31.152 |
From the table it can be seen that 4 is lower in energy when compared to 3 by 4.533 kcal/mol. It can also be seen that the largest contributor to both energies is the "bend' energy, and product 3 has a larger bend energy by 5.336 kcal/mol. The origin of this can be found by considering bond angles on an ideal alkene.

An SP2 carbon prefers to have bond angles of 120o, but product 3 has an average SP2 bond angle of 108o and product 4 of 112.5o. This means that both compounds experience strain which increase their energy. Product 3 will experience the largest strain because it deviates the most from the ideal angle of 120o. This results in product 4 being favoured over 3 when under thermodynamic control.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Introduction
A key intermediate in the synthesis of Taxol, a drug used to treat ovarian cancer, is an atropisomer. The isomers are outlined below, one having the carbonyl "up" and the other "down"; the least stable (kinetic product) converts to the most stable (thermodynamic product) on standing.
Jmol for structure (9)
Jmol for structure (10)
The Intermediates
The following reaction scheme shows how the intermediates 9 and 10 are formed from an oxy cope rearrangement (a [3,3] sigmatropic rearrangement).
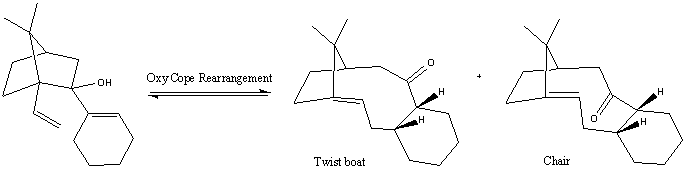
The products of the rearrangement, 9 and 10, are examples of bridgehead olefins. Bridgehead olefins are significant as they prove to be less strained and hyperstable compared to the hydrocarbon they were derived from, which accounts for their slow reaction rates. [5] [6] Although at a glance it appears that there are only two isomers of the Taxol intermediate, further investigation has found that 9 and 10 also contain different conformers, making the total of isomers at least 6.[7] They are all outlined below:
| Product 9 | 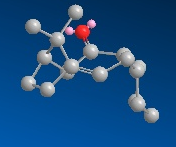 |
 |
 |
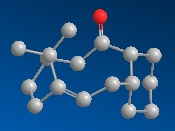
| Product 10 |  |
 |
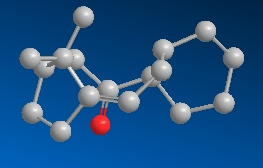 |
The table below outlines the properties of each conformer of isomer 9. The chair conformers have the cyclohexane ring in the chair form. 'Towards' refers to the carbonyl being towards the ring, when analysed as in the above pictures. Both MM2 and MMFF94 minimisations were performed, with MM2 giving details on stretch, bend, torsion, VDW, Dipole Dipole and an overall energy, and MMFF94 giving the enthalpy of formation.
| ' | 9 - Chair towards | 9 - Chair away | 9 - Twist Boat | 10 - Chair towards | 10 - Chair away | 10 - Twist Boat |
| Stretch | 2.783 | 3.015 | 3.074 | 2.621 | 2.902 | 2.912 |
| Bend | 16.536 | 19.367 | 19.508 | 11.343 | 16.680 | 16.800 |
| Stretch - Bend | 0.430 | 0.269 | 0.288 | 0.344 | 0.400 | 0.441 |
| Torsion | 18.258 | 18.586 | 20.508 | 19.67 | 17.427 | 20.245 |
| Non - 1, 4 VDW | -1.552 | -0.558 | -0.292 | -2.165 | -0.228 | 0.125 |
| 1, 4 VDW | 13.109 | 14.058 | 15.221 | 12.872 | 13.040 | 14.363 |
| Dipole/ Dipole | -1.725 | -1.712 | -1.720 | -2.002 | -1.808 | -1.721 |
| Total Energy (kcal/mol) | 47.840 | 53.024 | 56.588 | 42.683 | 48.406 | 53.165 |
| MMF94 Final Energy (kcal/mol) | 70.537 | 76.453 | 81.284 | 60.563 | 70.654 | 77.879 |
Although MM2 and MMFF94 energies cannot be compared, we can look at the general trends between isomers. Looking at product 9, it can be seen that the lowest energy conformer is "chair towards" for both the MM2 and MMFF94 methods and "twist boat" is the highest in energy in both methods. The same trend is seen in product 10, where both methods also give "chair towards" as the most stable and "twist boat" as the least. Overall, product 10's "chair towards" is the most stable isomer, and will thus be the thermodynamic product, suggesting that product 9 "chair towards" will form first before converting to 10. The other isomers are not observed as they are high in energy.
In order to prove the previously stated hypothesis that the alkene is more stable than its parent hydrocarbon, MM2 and MMFF94 calculations were performed on the hydrocarbon of the most stable isomer of 9 and 10. Unfortunately, product 10 immediately changes conformation to have the carbonyl up and the program would not accept it down no matter the amount of conformational changes tried, inadvertantly proving that it is of too high an energy to be favourable. Below is the comparison of 9 "chair towards" and its hydrogenated form; Jmol for hydrogenated 9. .
| Product 9 | Hydrogenated Product 9 | |
| Stretch | 2.783 | 2.969 |
| Bend | 16.540 | 17.66 |
| Stretch - Bend | 0.430 | 0.680 |
| Torsion | 18.255 | 23.071 |
| Non - 1, 4 VDW | -1.553 | -1.436 |
| 1, 4 VDW | 13.110 | 16.123 |
| Dipole/ Dipole | -1.725 | -1.774 |
| Total Energy (kcal/mol) | 47.840 | 57.300 |
| MMF94 Final Energy (kcal/mol) | 70.537 | 81.799 |
As you can see from the table, the hypthesis was proven, and both MM2 and MMFF94 show that the bridgehead olefin 9 is more stable than its hydrogenated form.
Semi Empirical and DFT molecular orbital theory
Regioselective Addition of Dichlorocarbene
The reaction of dichlorocarbene with electrophilic Dichlorocarbene with compound 12 (outlined below) contains orbital control. In order to show the implcations of orbital control, compound 12 will be modelled to find its preferred geometry and the energy of its orbitals. MM2 was used to "clean up" the geometry before using MOPAC PM6 and RM1. Analysis of the HOMO will indicate the reasons behind the selectivity that is shown in the reaction scheme below.[8]

Modelling of the Molecular Orbitals
An attempt was made to calculate the frontier orbitals of Dichlorocarbene using the PM6 - MOPAC method, however a bug in the system meant that the molecular orbitals were not symetrical. Instead, the RM1 - MOPAC method was used successfully. To compare, gaussview was also used to calculate the frontier orbitals. The results are shown below:
| Comparison of two methods to determine Frontier Orbitals of Compound 12 | |||||||
| MOPAC - RM1 | 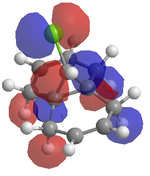 |
 |
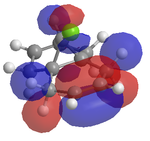 |
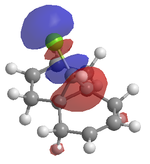 |
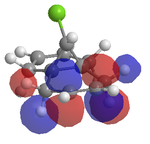 |
 | |
| Gaussview |  |
 |
 |
 |
 |
 | |
Looking at the HOMO produced in ChemBio 3D, it can easily be seen that the most nucleophilic C=C is by far the endo one, and thus the electrophile will prefer to attack here. Looking at the LUMO+1, the exo C=C can be seen to be less nucleophilic as it has a stabalisation from the C-Cl sigma star orital.
Vibrational Spectra
The vibrational spectra of Compound 12 and the monoalkene of 12 were produced in order to investigate the C-Cl bond influence on the vibrational frequencies of the molecule.
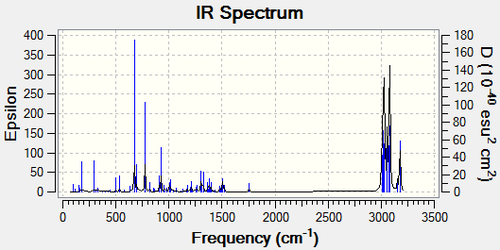
The two common stretches are that of the C=C on the side of the Cl, and the C-Cl stretch. The C=C stretch is very similar in the mono alkene, and is only 0.7cm-1 more. However, the C-Cl stretch of the monoalkene is 4.11cm-1 higher.
This is most likely due to the electron donation of the exo C=C pi orbital into the sigma star of the C-Cl, an interaction that isn't present in the monoalkene. The removal of this interaction means that the C-Cl bond is stronger, as its bond order is higher. There are more stretches present in the IR of the Monoalkene because it has more hydrogens present and more freedom to move.
Monosaccharide chemistry: glycosidation
Introduction
Glycosidation is the formation of a glycoside. The specific reaction that will be examined is outlined below[9]
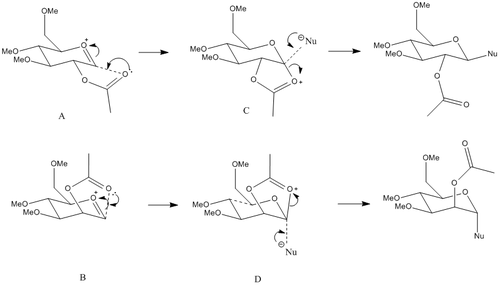
From this you can see that there are two possible anomers produced. Each anomer can undergo ring flipping, leading to 4 possible starting materials and 4 possible intermediates, all outlined below:

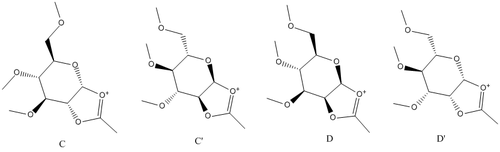
Modelling
Below is a table outlining the calculated energies for each conformer of A and B, using both MM2 and MOPAC. The R group was chosen to be Me as H is not a protecting group and higher R make the model complex. MOPAC considers electronic effects and therefore should be a more accurate method of calculation than MM2 for C and D.
| ' | A | A' | B | B' |
| Stretch | 2.244 | 2.536 | 2.441 | 2.610 |
| Bend | 9.779 | 13.183 | 12.934 | 14.407 |
| Stretch - Bend | 0.839 | 1.093 | 0.975 | 1.0318 |
| Torsion | 1.280 | 2.1714 | 0.064 | -0.088 |
| Non - 1, 4 VDW | -3.561 | -2.972 | -2.043 | -1.795 |
| 1, 4 VDW | 19.087 | 18.449 | 18.415 | 17.943 |
| Charge/ Dipole | 0.760 | 8.051 | -2.975 | -1.645 |
| Dipole/ Dipole | 4.368 | 4.555 | 6.583 | 7.692 |
| Total Energy (kcal/mol) | 34.797 | 47.067 | 36.394 | 40.155 |
| Heat of formation (kcal/mol) | -85.752 | -67.697 | -68.230 | -68.233 |
Considering the energies of A and B, it can be said that overall B/B' is lower in energy for MM2 and MOPAC, although A is the lowest conformation overall. Due to the many positions the OMe can take up, there is a wide variety of energies that each confomer can have.
| ' | C | C' | D | D' |
| Stretch | 2.030 | 2.050 | 1.844 | 2.050 |
| Bend | 13.153 | 13.920 | 13.566 | 14.231 |
| Stretch - Bend | 0.684 | 0.715 | 0.629 | 0.789 |
| Torsion | 7.314 | 8.151 | 7.84 | 9.596 |
| Non - 1, 4 VDW | -1.919 | -2.019 | -4.7-6 | -4.928 |
| 1, 4 VDW | 17.729 | 17.880 | 18.364 | 17.784 |
| Charge/ Dipole | -13.494 | -12.302 | 1.823 | 8.060 |
| Dipole/ Dipole | -0.637 | -1.807 | 0.002 | -1.591 |
| Total Energy (kcal/mol) | 24.860 | 26.586 | 38.605 | 45.992 |
| Heat of formation (kcal/mol) | -91.660 | -91.652 | -90.513 | -91.642 |
Here it can be seen that the lowest conformer is C for MM2 and D for MOPAC. There is no real trend between MOPAC and MM2. Although I previously stated the MOPAC would be more effective at deciding the lowest energy conformer, I believe that the lowest in energy should be C or C', not D. This is because, using my chemical knowledge, there is an anomeric effect that stablaises the C conformer.
Structure based Mini Project: Reaction of 2,5- Bis(methoxycarbonyl)-3,4-diphenylcyclopentadienone with 1-Ethynylcyclohexylamine
Introduction
The reaction of 2,5- Bis(methoxycarbonyl)-3,4-diphenylcyclopentadienone (1) with 1-Ethynylcyclohexylamine (2) is pericyclic and produces a mixture of compounds. One is Spiro(cyclohexane-1, 4, (2-oxo-9c-phenyl-2, 3, 4, 9c - tetrahydro - (2aa, 9ca) - 3 aza- pentaleno91,6-ab)napthalene) - 1, 2a - dicarboxylic acid dimethyl ester, which will be refered to as 3. The second is Spiro (cyclohexane- 1, 4 -(3 methylene - 4 - oxo - 6, 6a- diphenyl- 2, 3, 4, 6a - tetrahydo - 3aa, 6aa) - 1H cyclopenta (b) pyrrole)- 3a, 5- dicarboxylic Acid Dimethylester, which be referred to as 4. [10]
Intramolecular [4+2] π cycloaddition of the [1,5]-sigmatropic rearrangement products of the 1,4 adducts of 1 and 2, followed by the [1,5]-sigmatropic rearrangement of hydrogen and dehydrogenation yields 3.
4 is synthesised from the [2π, 2π, 2σ] reaction of 1 and 2.

Differentiating between isomeric products
IR Spectroscopy
IR spectroscopy is as useful technique to distinguish between functional group isomers by considering their characteristic peaks. The only functional group that differs between 3 and 4 is the C=C on 4. The reported IR peaks are not for different functional groups and the values do not differ significantly between products.
The following is the computationally predicted IR spectra of Product 3:
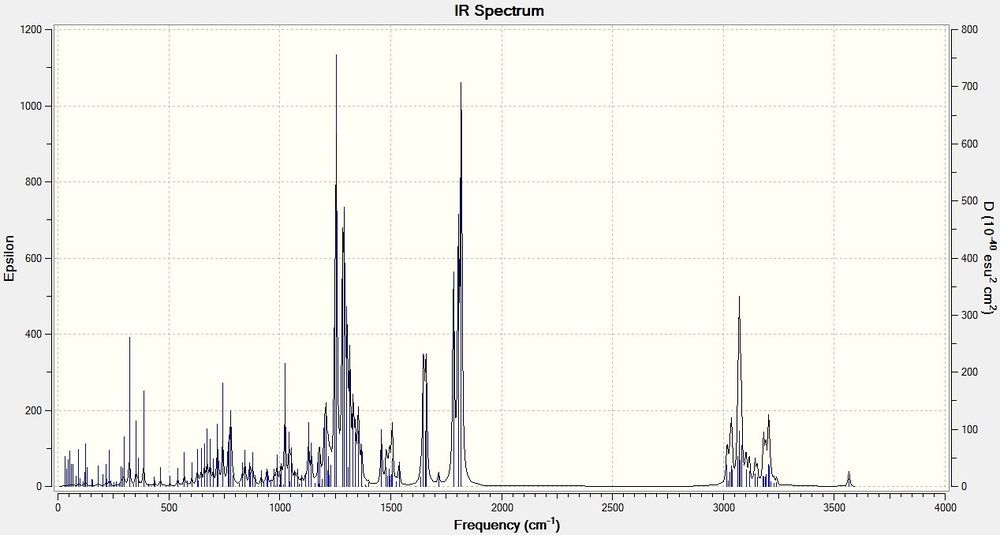
The important peaks that are present are 1805 (C=O) and COO (1783).
The following is the computationally predicted IR spectra of Product 4:
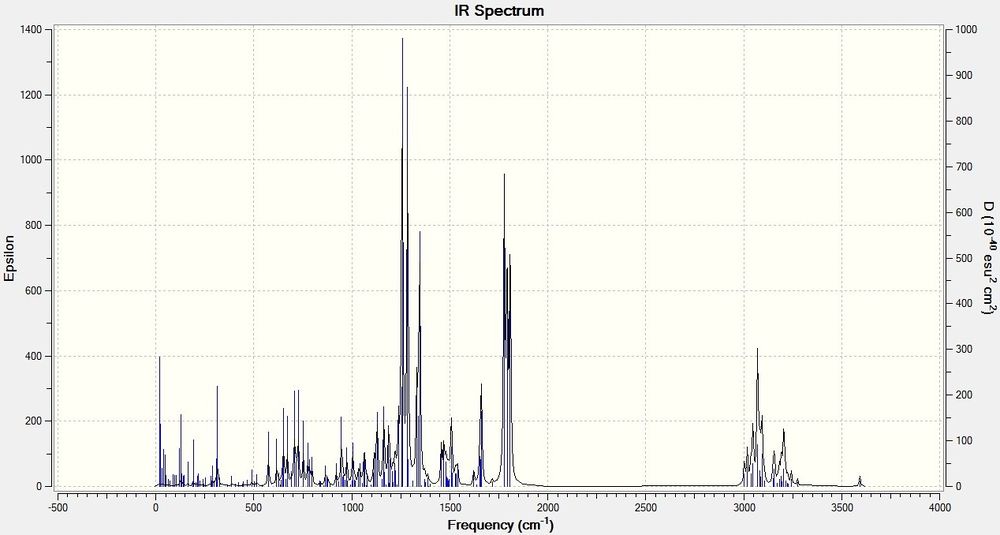
The important peaks that can be seen in the above spectra are 1777 (C=O) and 1792, 1808 (COO).
The following table summmarises the stretches observed for both 3 and 4 and compares the experimental values to the computational values.
| ' | Experimental | Computational | Corrected Computational |
| 3g C=O | 1624 | 1805 | 1660 |
| 3g COO | 1724 | 1783 | 1640 |
| 5g C=O | 1602 | 1777 | 1634 |
| 5g COO | 1722 | 1792, 1808 | 1648, 1663 |
| 5g C=C | - | 1716 | 1578 |
There are peaks present in the computational IR at the values for the experimental but their assignments are different. For example, the experimental assignment for a peak at 1724 is COO vibration, however the computational IR assigns a peak at 1716 to be the C=C stretch outlined in the below picture:
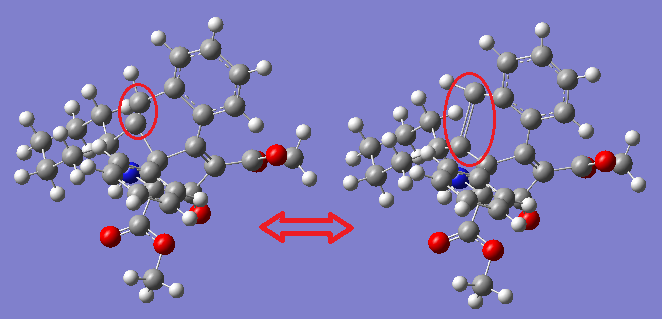
This can be explained by considering the nature of the vibrations. They are all stretches, and stretches give a systematically high value. On reducing the computational values by 8%, more reasonable values are obtained.
NMR Spectroscopy
The 13C NMR of 3 and4 should differ significantly and therefore it is a good method to distinguish between the isomers.

The above diagram is colour coded, with red carbons being in pretty much the same environment in both isomers. The other carbons should produce differing peaks.
Below is a table showing the assigned peaks for each carbon on each isomer:
| nothing | 3 | 4 | ||||||
|---|---|---|---|---|---|---|---|---|
| C Type | comp | correct | experiment | C Type | comp | correct | experiment | |
| C# | shift | C# | shift | |||||
| Aryl | ||||||||
| 1 | 130.1 | 130.1 | 127.2 | 1 | 128.2 | 128.2 | 126.9 | |
| 2 | 125.8 | 125.8 | 2 | 127.5 | 127.5 | |||
| 3 | 131.6 | 131.6 | 127.3 | 3 | 127.0 | 127.0 | 128.4 | |
| 4 | 125.4 | 125.4 | 127.4 | 4 | 125.9 | 125.9 | ||
| 5 | 133.3 | 133.3 | 5 | 126.4 | 126.4 | |||
| 6 | 125.6 | 125.6 | 127.4 | 6 | 128.4 | 128.4 | 128.7 | |
| 7 | 120.1 | 120.1 | 7 | 126.7 | 126.7 | |||
| 8 | 155.7 | 155.7 | 8 | 129.7 | 129.7 | |||
| 10 | 181.9 | 181.9 | 127.8 | 9 | 126.4 | 126.4 | 129.5 | |
| 26 | 132.8 | 132.8 | 10 | 129.5 | 129.5 | |||
| 27 | 130.6 | 130.6 | 33 | 134.4 | 134.4 | |||
| 28 | 124.4 | 124.4 | 129.0 | 34 | 131.3 | 131.3 | 120.9 | |
| 29 | 126.0 | 126.0 | ||||||
| 30 | 125.6 | 125.6 | ||||||
| 31 | 125.8 | 125.8 | 131.8 | |||||
| C=O | 14 | 191.0 | 191.0 | 200.2 | 21 | 188.4 | 193.1 | 194.0 |
| COO | 22 | 171.2 | 176.6 | 171.0 | 35 | 165.9 | 171.5 | 168.0 |
| 32 | 162.8 | 168.5 | 161.0 | 32 | 168.9 | 174.3 | 164.0 | |
| Spiro | 17 | 40.8 | 40.8 | 40.5 | 27 | 43.7 | 43.7 | 40.5 |
| 18 | 26.5 | 26.5 | 25.0 | 28 | 24.8 | 24.8 | 25.0 | |
| 19 | 27.8 | 27.8 | 22.9 | 29 | 28.0 | 28.0 | 22.9 | |
| 20 | 26.1 | 26.1 | 39.6 | 30 | 27.1 | 27.1 | 39.6 | |
| 21 | 32.7 | 32.7 | 31 | 38.9 | 38.9 | |||
| Quaternary | 9 | 70.6 | 70.6 | 126.8 | 19 | 85.9 | 85.9 | 132.1 |
| 11 | 72.3 | 72.3 | 129.1 | 20 | 82.9 | 82.9 | 131.5 | |
| 13 | 82.4 | 82.4 | 134.4 | 23 | 71.8 | 71.8 | 139.2 | |
| ? | 136.9 | |||||||
| OCH3 | 25 | 54.2 | 54.2 | 52.0 | 16 | 59.1 | 59.1 | 57.0 |
| 35 | 55.6 | 55.6 | 52.0 | 13 | 55.8 | 55.8 | 52.0 | |
| CR2CCOOCH3 | 15 | 126.1 | 126.1 | ? | 17 | 134.4 | 134.4 | 154 |
| CR2CH2 | 26 | 114.0 | 114.0 | 74.0 | ||||
| CR2CH2 | 24 | 153.9 | 153.9 | 174.0 | ||||
| PgCCR2 | 18 | 174.4 | 174.4 | ? | ||||
From the table it can be seen that the experimental data does not assign all Aryl peaks, or specific Spiro Cs or quarternary Cs. All carbons for both isomers are assigned computationally.
In general, the agreement is good. The results for Cs attached to a C=O were corrected by +5ppm.
Considering product 3, C14 obtains very close to the experimental value of 200.2, at 195.6. The difference of 5ppm is likely to be due to the systematic error of +5ppm for carbonyls. This is also the case for both carbonyl carbons on the ester groups. However, after correction, C22 is out by 5.6ppm and C32 is out by 7.5ppm, and therefore agree better before the correction. C25 and C35 have excellent agreements within 3ppm.
The main problem I have with the experimental assignment, is that they have allocated 4 shifts to the "Quaternary C" section, when only 3 quaternary carbons are present. I do not know how to account for this.
Considering product 4, C21 (after correction) is 1ppm different from the experimental value. As in 3 's assignment, the carbons on the ester chain (C35 and C32) actually agree better without the correction, and are within the range of error. With the correction, C32 is 10ppm different. C26 and C24 have very poor agreements. C26 differs from experimental by -44ppm and C26 by +30ppm. C16 and C13 differ from their experimental values by -2.1 and -3.8ppm respectively.
The differences between computational and experimental shift values can be down to the molecules uploaded to assign the NMR having slightly different conformations to the product synthesised.
Below is a diagram showing carbon labels to help illustrate the table above.
5g labelled for nmr jb.PNG


The following table shows the carbons that are not in a similar environment compared on the other isomer. There isnt a great deal of difference between the carbons on phenyl rings, or the quaternary carbon. However, 4 contains an alkene out of the cyclopentane ring, giving it unique peaks, and enabling it to be distinguished from its isomer.
| ' | 3 | ' | 4 | ' |
| C # | Shift (ppm) | C # | Shift (ppm) | |
| Quarternary C | 13 | 82.4 | 19 | 85.9 |
| Aryl | 1 | 130.1 | 6 | 128.4 |
| 2 | 125.8 | 7 | 126.7 | |
| 3 | 131.6 | 8 | 129.7 | |
| 4 | 125.4 | 9 | 126.4 | |
| 5 | 133.3 | 10 | 129.5 | |
| 6 | 125.6 | 34 | 131.3 | |
| 7 | 120.1 | |||
| 8 | 155.7 | |||
| CR2CH2 | 26 | 114.0 | ||
| CR2CH2 | 24 | 153.9 | ||

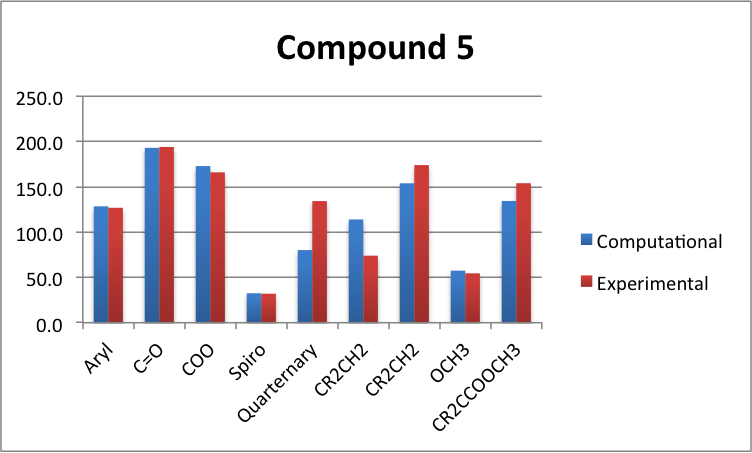
As you can see from the above graphs, compound 3 agrees within a certain degree of accuracy except for the quaternary Cs which have a massive disagrement. Compound 4's graph also shows that the quaternary Cs have a poor agreement, as does the CR2=CH2. This is probably due to conformation, and the modelled molecule is probably a slightly different conformation to the experimental one.
Product 3g |
Jmol for Product 3
Product 5g |
Jmol for Product 4
The Mechanism of the Reaction

Conclusion
Although experimentally it is easy to detect the difference between isomers 3 and 4, computationally it is not so easy. The NMRs are definitely different but the quarternary Cs are not in great agreement. Other Cs can be analysed to determine which isomer is present. IR cannot be used computationally or experimentally to distinguish the compounds.
References
- ↑ Computational Chemistry - A Practical Guide for Applying Techniques to Real World Problems, David Young, 2001
- ↑ Industrial organic chemistry by Klaus Weissermel and Hans Jurgen Arpe
- ↑ Cycloadditions. IX. Mechanism of the Thermal Interconversion of exo-and endo-Dicyclopentadiene by J.E.Baldwin
- ↑ Organic Chemistry - Clayden, Greeves, Warren and Wothers, p908
- ↑ Methods for the Preparation of Bridgehead Olefins By Reinhart Keese
- ↑ Evaluation and Prediction of the Stability of the Bridgehead Olefin, Wilheim F Maier and Paul von Rague Schleyer
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0
- ↑ A molecular orbital and crystallographic study of the structure and π-facial regioselectivity of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene, Brian Halton, Roland Boese and Henry S. Rzepa J. Chem. Soc., Perkin Trans. 2, 1992, 447-448, DOI: 10.1039/P29920000447
- ↑ M.Whitfield T Nukads Carbohydr. Res. 2007, 342, 1291, DOI:10.1016/].carres.2007.03.030
- ↑ Yasuyuki Yoshitake, Kouki Yamaguchi, Chika Kai, Takayo Akiyama, Chiaki Handa, Tamaki Jikyo, and Kazunobu Harano, Cyclization of Electron-Deficient Cyclopentadienone with 2-Alkenyl and 2-Alkynylamines via Sequential Pericyclic Reaction Pathway, J. Org. Chem. 2001, 66, 8902-8911
