Rep:Mod:mmo116
Ammonia, NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
final energy E(RB3LYP): -56.56045780 a.u.
RMS gradient: 0.00015033 a.u.
Point group: C3V
Optimised N-H bond distance = 1.01881
Optimised H-N-H bond angle = 104.941
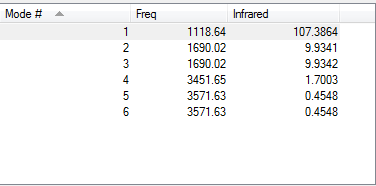
The following table shows that the molecule is converged:
Item Value Threshold Converged? Maximum Force 0.000263 0.000450 YES RMS Force 0.000173 0.000300 YES Maximum Displacement 0.000569 0.001800 YES RMS Displacement 0.000377 0.001200 YES
The next table proves that there are no negative frequencies:
The expected number of modes (calculated using the (3N-6) rule) = 3(3) - 6 = 3 modes.
In this case, modes 2 and 3 as well as 5 and 6 are degenerate.
The bending modes are at a frequency of ~1000 cm-1 which means modes 1, 2 and 3 are bending.
The stretching modes are at a frequency of ~3000 cm-1 which means modes 4, 5 and 6 are stretching.
Mode 4 is highly symmetric.
Mode 1 is the umbrella mode.
You'd expect to see 6 bands in an experimental spectrum of gaseous ammonia.
Charges on Atoms
N: -1.131 H: 0.377
The electronegativity of n is 3.04 and of H is 2.20. As the electronegativity of N is higher, it is expected that the n atom will be the one with the negative charge and the H atoms positive. This backs up the charges calculated using Gaussian. When you multiply the charge on a H atom by 3 (there are 3 H atoms) the value of the charge is the same as the charge on the N atom with the opposite sign. This also backs up the calculated charges because it adds up that the overall charge on the molecule is 0 which is true. [1]
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedElectronegativity
NH3 optimisation |
N2 and H2
H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
final energy E(RB3LYP): -1.17853936 a.u.
RMS gradient: 0.00000017 a.u.
Point group: D*H
Optimised H-H bond separation = 0.74279
The following table shows that the molecule is converged:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The next table proves that there are no negative frequencies:
H2 optimisation |
N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
final energy E(RB3LYP):-109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D*H
The following table shows that the molecule is converged:
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The next table proves that there are no negative frequencies:
N2 optimisation |
Energy for Reaction of N2 + 3H2 -> 2NH3
E(NH3)= -56.56045780
2*E(NH3)= -113.1209156
E(N2)= -109.52412868
E(H2)= -1.17853936
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.06116884 a.u.
ΔE= -160.60 kJ/mol
Due to the fact that the change in energy for the reaction is negative - meaning the reaction is exothermic - the product is more stable. The gaseous reactants are less stable than the ammonia product.
Project Molecule - F2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
final energy E(RB3LYP): -199.49825218 a.u.
RMS gradient: 0.00007365 a.u.
Point group: D*H
Optimised F-F bond distance = 1.40281
The following table shows that the molecule is converged:
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
The next table proves that there are no negative frequencies:
F2 optimisation |
Both F atoms have a zero charge. This is unsurprising considering F2 is a molecule comprised of 2 of the same atom so there should be nothing that distinguishes between the 2 causing one to have a different charge to the other. The overall charge of the molecule is zero so the charges on both individual atoms should be too. The charge distribution is shown in the image below.
Molecular Orbitals
Fluorine has an electronic configuration of 1s2 2s2 2p5
Molecular Orbital 1
The first molecular orbital is a bonding orbital made up of the two 1s atomic orbitals. The energy of this molecular orbital is very deep (-21.79730 a.u.), the deepest of all the molecular orbitals. It is occupied however it is not useful in bonding. The orbitals can't be fully seen in the diagram which means they are very tightly held to the nuclei.
Molecular Orbital 3
The third molecular orbital is a bonding molecular orbital comprised of two 2s atomic orbitals and is occupied. The energy is much higher than that of the first two molecular orbitals at -1.33659 a.u.. It is much closer in energy to the other, higher orbitals than it is to the lower orbitals. It's much more useful in bonding than the lower orbitals due to the higher energy and the fact it is less tightly bound to the nuclei.
Molecular Orbital 4
The fourth molecular orbital is also comprised of the two 2s atomic orbitals but in this case, it is antibonding. The molecular orbital is filled and has a higher energy than the third molecular orbital but with a much smaller energy gap than between the second and third molecular orbitals. the energy of this molecular orbital is -1.09047 a.u.. This molecular orbital is also more useful in bonding.
Molecular Orbital 7
Molecular orbital 7 is the first molecular orbital looked at in this report made up of 2p atomic orbitals. The 2p atomic orbitals are perpendicular to the bond and in the right orientation to form a bonding orbital. This molecular orbital is a pi molecular orbital and is degenerate with another pi molecular orbital which is made of the other set of 2p orbitals perpendicular to the bond. Both of these have energies of -0.52332 a.u. and are very useful in bonding. They aren't held too close to the nuclei and the energy is higher than the third and fourth molecular orbitals making it more accessible.
Molecular Orbital 10
This molecular orbital is the first unoccupied orbital looked at and is also the LUMO for F2. It's an antibonding orbital made up of two 2p atomic orbitals arranged along the bond. It's the highest negative energy orbital at -0.12679 a.u. and particularly useful in bonding as it can accept two electrons but isn't too high in energy.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedMOs