Rep:Mod:mmn115

NH₃ molecule

General information about the optimised molecule

NH₃ calculation summary

Molecule	NH3
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final energy E(RB3LYP)	-56.55776873 a.u.
Point group	C3V
RMS Gradient	0.00000485 a.u.
N-H bond length	1.01798 Å
H-N-H bond angle	105.741°

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

Jmol ammonia molecule visualisation

The optimisation file is linked to here

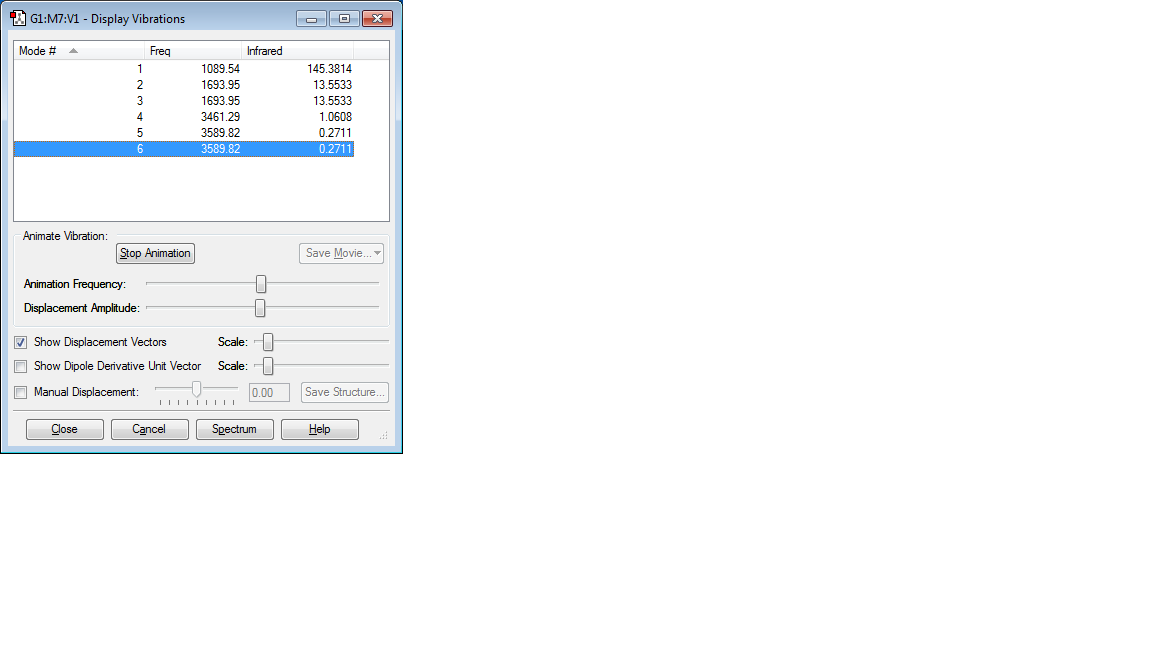
Vibrations of the molecule

We are expecting six modes of vibrations of the molecule based on the 3N-6 rule (3*4-6=12-6=6). The following modes are degenerate: 2 and 3; 5 and 6

The following modes are bending vibrations: 1, 2, 3,

The following modes are stretching vibrations: 4, 5, 6,

Mode number 4 is highly symmetric. Mode number 1 is known as the umbrella mode.

You are expected to see two bands in an experimental spectrum of gaseous ammonia. This is because the symmetric stretch (mode number 4) is not observed in the IR spectrum, as it does not involve a change in dipole moment of the molecule. Mode number 5 and mode number 6 have such low intensities (0.2711) that they would not be observed either. Modes 2 and 3 are degenerate (both have an intensity of 13.5533)so the would create one peak in the IR spectrum. This leaves us with two peaks: one for mode number 1 and one for modes 2 and 3.

Charge Analysis

Charge on N atom: -1.125 Charge on H atom: 0.375

We would expect the charge on the N atom to have a negative value and the H atom to have a positive value. This is because N is more electronegative than H, hence it will pull electron density towards itself. This expectation agrees with the data obtained from the calculations.

The Haber-Bosch process

N₂ molecule analysis

General information about the optimised molecule

N₂ calculation summary

Molecule	N2
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final energy E(RB3LYP)	-109.52412868 a.u.
Point group	D∞h
RMS gradient	0.00000060 a.u.
N-N bond length	1.10550 Å
N-N bond angle	it is a linear molecule

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

Jmol nitrogen molecule visualisation

The optimisation file is linked to here

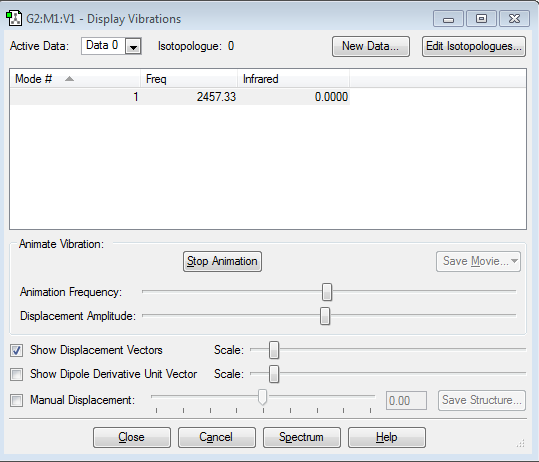
Vibrations of the molecule

From the 3N-5 rule we expect one vibrational mode (3*2-5=6-5=1), which fits with the data obtained from the calculations. It is a stretching vibration. This vibrational mode would not be observed in the IR spectrum, because it is symmetrical and therefore would not involve a change in dipole.

Charge Analysis

The molecule is electrically neutral because it is homonuclear, so the charge is distributed equally over the two identical nitrogen atoms.

H₂ molecule analysis

General information about the optimised molecule

H₂ calculation summary

Molecule	H2
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final energy E(RB3LYP)	-1.17853936 a.u.
Point group	D∞h
RMS gradient	0.00000017 a.u.
H-H bond length	0.74279 Å
H-H bond angle	it is a linear molecule

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Jmol hydrogen moleculevisualisation

The optimisation file is linked to here

Vibrations of the molecule

We are expecting to see one vibrational mode due to the 3N-5 rule (3*2-5=6=5=1), which agrees with the results obtained. It is a stretching vibration. This vibrational mode would not be observed in the IR spectrum, because it is symmetrical and therefore would not involve a change in dipole.

Charge Analysis

The molecule is electrically neutral because it is homonuclear, so the charge is distributed equally over the two identical hydrogen atoms.

Energies in the Haber-Bosch process

E(NH3)=-56.55776873 a.u.

2*E(NH3)=-113.11553746 a.u.

E(N2)=-109.52412868 a.u.

E(H2)=-1.17853936 a.u.

3*E(H2)=-3.53561808 a.u.

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-113.11553746-(-109.52412868-3.53561808)= -0.055790700 a.u.

We now want to convert atomic units to kJ/mol. We know that 0.01 kJ/mol is 0.0000038 a.u. So ΔE[kJ/mol]=(0.01*-0.055790700)/(0.0000038)=-146.82 kJ/mol We can see that the ammonia product is more stable than the gaseous reactants. This is because 146.82 kJ of energy are released for every mole of reactants reacting, hence the final product (ammonia) will be lower in energy, more stable.

Comparison with a literature value

The enthalpy change for the Haber process calculated above is -146.82 kJ/mol. However, the literature value is -92 kJ/mol.

The theoretical value obtained in the calculations is lower than the literature value. This could be because our calculations did not take into account the entropy change involved in this process: we went from four molecules of gas to two molecules of gas so there was a decrease in entropy. The entropy change might have largely contributed to the enthalpy change (it lowered it). The literature value could have taken into account this entropy change and the enthalpy change value is therefore lower than ours.

Project molecule S₂

General information about the optimised molecule

NH₃ calculation summary

Molecule	S2
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final energy E(RB3LYP)	-796.32599779 a.u.
Point group	D∞h
RMS Gradient	0.00000372 a.u.
S-S bond length	1.92943 Å
S-S bond angle	it is a linear molecule

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000011     0.001800     YES
 RMS     Displacement     0.000016     0.001200     YES

jMol sulfur molecule visualisation

The optimisation file is liked to here

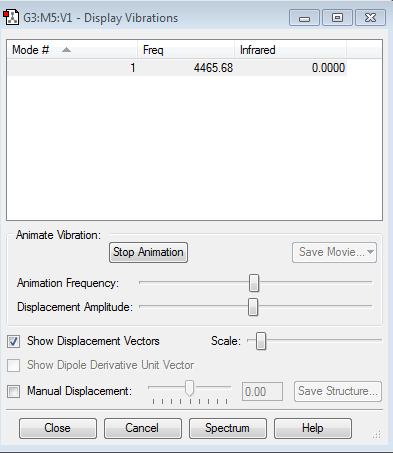
Vibrations of the molecule

We are expecting to see one vibrational mode due to the 3N-5 rule (3*2-5=6=5=1), which agrees with the results obtained. It is a stretching vibration. This vibrational mode would not be observed in the IR spectrum, because it is symmetrical and therefore would not involve a change in dipole.

Charge Analysis

The molecule is electrically neutral because it is homonuclear, so the charge is distributed equally over the two identical sulfur atoms.

Molecular orbital analysis

1. A Gaussview image of the 3σ_g MO.

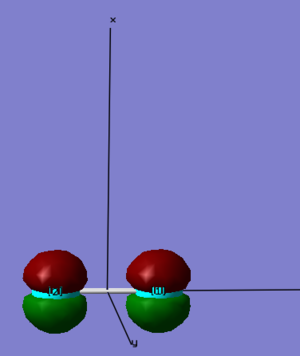
1. This Molecular Orbital (MO) comes from the sideways overlap of two 2p orbitals. When we add the cartesian coordinates to the diagram, we see that it's the two 2p_x orbitals. We can also tell that the Atomic Orbitals (AO) combined in phase (the AOs have the same sign above and below the internuclear axis: both are red above the axis and green below the axis), which means that it is a bonding orbital. Putting this information together we can tell that this is the 3σ_g bonding molecular orbital. Although it is occupied and has two electrons in it, it does not form a bond for two reasons:

(1) we can see in the diagram that the 2p orbitals are too small to overlap and there is no electron density in between the atoms

(2) the two electrons in the bonding 3σ_g are cancelled out by the two electrons in the antibonding 3σ_u*

It is relatively low in energy (-5.96349 a.u.), and is neither a HOMO nor a LUMO. There are five other MOs that are similar in energy to this one: two 1π_u, two 1π_g and 3σ_u*.

2. A Gaussview image of the 4σ_g MO.

2. This MO comes from two 3s AOs overlapping in phase, which means that the two AOs had the same sign (same colour in the diagram). Looking at the diagram we can see that there is electron density between the two nuclei which results in a bonding situation. This gives us a 4σ_g filled bonding orbital with two electrons in it. It energy is equal to -0.39516, which is significantly higher than that of 3σ_g. It's neither a HOMO nor a LUMO.

3. A Gaussview image of the 2π_g* MO.

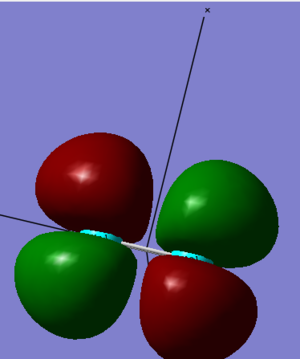
3. This MO comes from the sideways overlap of two 3p_x orbitals. They are overlapping out of phase (the signs are different above and below the internuclear axis), which means that it is an antibonding orbital. Putting this together we know that it's a 2π_g* antibonding MO. It doesn't accommodate any electrons and is the LUMO with an energy of -0.18463 a.u.

4. A Gaussview image of the 5σ_g MO.

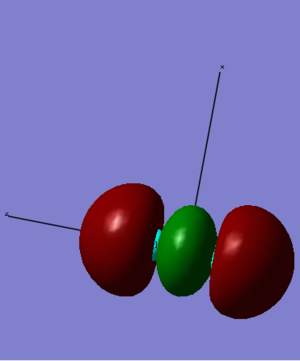
4. This MO comes from the head-on overlap of two 3p_z orbitals. The two orbitals combined in phase and result in an electron density in between the atoms, so we can tell that this is the 5σ_g. This MO accommodates two electrons and creates the single σ bond between the two S atoms.

It is lower in energy than the 2π_g* antibonding MO with an energy value of -0.39516 a.u.. However, relative to other MOs, it is quite high in energy.

5. A Gaussview image of the 2π_u MO.

5. This is an MO that results from the sideways overlap of two 3p_x AOs. It is in phase and results in a bonding situation, as there is increased electron density between the two nuclei. We can tell that it is a 2π_u MO. It accommodates two electrons and results in a π bond between the two sulfur atoms. Therefore, from the MO diagram, we can assume that there is a double bond between the two S atoms. The second electron pair in the second 2π_u MO is cancelled out by the electron pair in the antibonding 2π_g* MO, and therefore does not result in a third bond between two S atoms.

Its energy is equal to -0.39516 a.u. and it is the 2nd highest in energy occupied MO.

Knowing all this, we can calculate the bond order of the S₂ molecule.

bond order=(18-14)/2=4/2=2