3rd Year Lab

Module 1: Organic

The Hydrogenation of Cyclopentadiene Dimers

Cyclopentadiene dimerises when left standing to forms an endo rather than an exo dimer. This dimer then hydorogenates regiospecifically. This reactivity will be investigated using MM2 molecular mechanics in the following questions.

The Optimisation of the Exo Dimer, Dimer 1

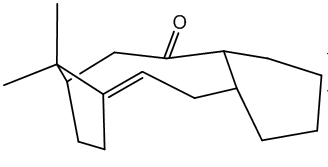
Dimer 1 was drawn in ChemBio3D and optimised using MM3 molecular mechanics as described[[1]. The breakdown of the energy calculated is shown below.The image of the dimer is conveniently available by clicking on the link below and then again on the blank box where you'd expect to see an image.

Cyclopenadiene Dimer 1

Conformation 1 MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.2923	0.002059442
Bend:	20.5870	0.032807968
Stretch-Bend:	-0.8413	-0.001340717
Torsion:	7.6715	0.012225498
Non-1,4 VDW:	-1.4358	-0.002288127
1,4 VDW:	4.2320	0.006744223
Dipole/Dipole:	0.3778	0.000602072
Total Energy:	31.8834	0.050810199

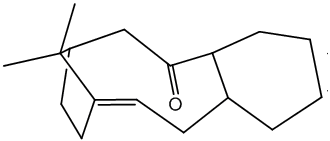
The Optimisation of the Endo Dimer, Dimer 2

The second dimer was optimised in an identical manner.

Cyclopentadiene Dimer 2

Conformation 1 MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.2454	0.001984701
Bend:	20.8603	0.033243506
Stretch-Bend:	-0.8320	-0.001325896
Torsion:	9.5039	0.015145657
Non-1,4 VDW:	-1.5083	-0.002403665
1,4 VDW:	4.3012	0.006854502
Dipole/Dipole:	0.4448	0.000708845
Total Energy:	34.0153	0.054207649

Discussion

Dimer 2, the endo dimer, is formed, despite being higher in energy. Consequently dimer 2 is the kinetic, rather than the thermodynamic product. This is as expected because the reaction proceeds as it does due to the interaction of specific phases of the p-molecular orbitals, as explained by frontier molecular orbital theory. These quantum mechanical considerations are not taken into account by the program, so predicting the result of such processes is beyond its scope.

Minimisation of energy of dimer 3

Dimer 3 was then minimised using MM3 molecular mechanics.

Cyclopentadiene dimer 3

Conformation 3 MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.2067	0.001923028
Bend:	18.8637	0.030061673
Stretch-Bend:	-0.7528	-0.001199681
Torsion:	12.2396	0.019505339
Non-1,4 VDW:	-1.5532	-0.002475219
1,4 VDW:	5.7649	0.009187092
Dipole/Dipole:	0.1632	0.00026008
Total Energy:	35.9322	0.05726247

The minimisation of dimer 4

The prodcedure was repeated for dimer 4.

Cyclopentadiene dimer 4

Dimer 4 MM2 Minimisation	Kcalmol-1	Hartrees
Stretch:	1.0973	0.001748685
Bend:	14.5063	0.02311761
Stretch-Bend:	-0.5494	-0.000875538
Torsion:	12.4976	0.019916494
Non-1,4 VDW:	-1.0512	-0.001675219
1,4 VDW:	4.5127	0.007191554
Dipole/Dipole:	0.1407	0.000224223
Total Energy:	31.1539	0.049647649

Dimer 4 is predicted by molecular modelling to be lower in energy so is consequently expected to be the thermodynamic product of the hydrogenation. This extra thermodynamic driving for would normally be expect to make the hydrogenation much more likely unless there are more important kinetic considerations, such as steric protection.

Analysis of the relative contributions to the energy

Stretching (str)

Dimer 3 has a slightly higher stretching energy than dimer 4.Dimer 3 is expected to be higher energy because the double bond occurs between to carbons that are components of a 6 membered ring AND a 5 membered ring, whereas the double bond in dimer 4occurs between to carbons that are members of just one cyclic system. This will raise the stretching energy in dimer 3 because a double bond is shorter than a single bond and when it occurs in a cyclic system, the bond will be under tension as the ring attempts to alleviate the strain caused by greater than 109° bond angles that are a result of the ring’s limit on free movement.

Bending (bnd)

The bending energy is the largest difference in energy between any component. As explained in the previous section, ring systems with a single π-bond cause a great deal bending strain as the atoms within the ring are forced to cope with a higher energy geometry due to a greater bond angle. A way of illustrating this is to imagine a normal cyclopentane ring (already fairly strained compared with cyclohexane) and imagine one bond is removed and replaced with a shorter bond. In order to maintain the continuous ring the ring must be tightened away from its optimum geometry and hence it is unsurprising that a ring with a single shorter bond, a π-bond, would be higher energy. In this specific example conformer 3 is higher energy because its π-bond occurs between 2 carbons that are involved in two cyclic systems, a cyclohexane and cyclopentane whereas the two carbons involved in π-bonding within dimer 4 are only involved in a single cyclohexane ring. Consequently it is unsurprising that dimer 4 is shown to have a significantly lower bending energy.

Torsion (tor)

There is little significant difference between the torsional strain of the two molecules, however both of these energies are rather high. This is because both molecules feature a double bond in a cyclopentane system and these bonds are forced to undergo a certain amount of twisting compared to a planer π-bond in a linear system due to the required shape of the ring. This π-bond torsional strain is high energy, but the torsion strain in dimer 3 is marginally lower in energy in dimer 3 because of the presence of the cyclohexane ring, because a 6 membered ring requires less of a twist than a 5 membered ring.

Van der Waals (vdw)

Van der Waals interactions in this context refer to steric repulsions between the molecules. Dimer 3 has slightly larger 1,4 van der Waals repulsions, meaning that the groups attached to the carbons forced into closer proximity by the shorter π-bond are moderately more significant. This can be rationalised by observing that both the substituents on the carbons either side of the double bond are branched in dimer 3, whereas the on one of the carbons partaking in π-bonding in dimer 4 the substituent is merely a carbon with a hydrogen (as well as the ring). This could explain why dimer 3 has a moderately higher 1,4 vdw energy.

Hydrogen bonding (H-Bond)

Hydrogen bonding requires a hydrogen attached to a very electrophillic substuent. This is not present in the molecule so this is not a significant factor in the selectivity of the hydrogenation.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Molecular mechanics was used to calculate the optimum geometries of substituted pyridium rings and hence give insight in their reactivities.

The first example investigated involved the sterioselective addition displayed below.

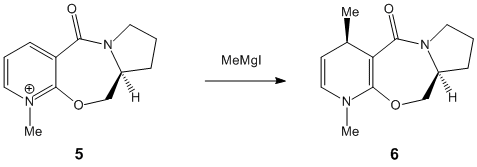
The reactant "5" was drawn and it's geometry was optimised using the MM3 molecular modelling technique employed by chembio3D.

A breakdown of the energy minimisation is shown below.

Dimer 4 MM2 Minimisation	Kcalmol-1	Hartrees
Stretch:	0.8750	0.001394
Bend:	6.8318	0.010887
Stretch-Bend:	0.1284	0.000205
Torsion:	9.6613	0.015396
Non-1,4 VDW:	-2.6515	-0.00423
1,4 VDW:	11.4847	0.018302
Charge/Dipole:	3.1421	0.005007
Dipole/Dipole:	-3.8135	-0.00608
Total Energy:	25.6583	0.04089

This optically active derivative of prolanol is found to undergo addition at the 4 position of the pyridine ring adding onto the face shown. This steriospecificity can be explained using molecular modelling. When the most stable special conformation is computed it can be seen that the carbonyl group sticks out on the same face as the methyl group is known to attack with a dihedral angle of 43°. Consequently it is reasonable to assume that the Grignard reagent in some way complexes to the lone pairs on the oxygen and is thus guided into attacking on the correct face. As the bond between the Mg and the carbon atom is conventionally thought of as having a high degree of ionic character it seems likely that the magnesium component in the molecule will be behave somewhat like a +MgI ion, ie it is electron deficient and likely to complex with a lewis base such as the carbonyl oxygen lone pairs.

Although molecular mechanics is an effective way to predict the correct special conformation of the molecule it is unable to compute the probably interactions with a metal ion such as the MeMgI. This is because bonds between metal ions are not similar to conventional carbon-carbon bonds and many other factors, neglected in molecular mechanics such as molecular orbital theory.

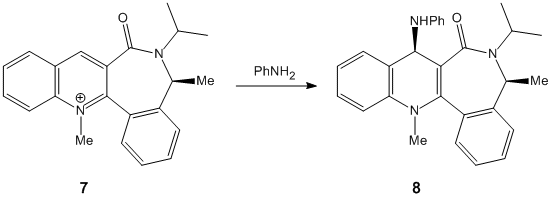
Derivative 7 can exist in 2 conformers, one where the Me group with the specified steriochemistry is axial, and one where that group is equatorial. The conformation where the methyl group is axial is high in energy due to the sizable steric repulsions from the isopropane substituent and the hydrogen jutting out from the neighbouring aromatic ring by an angle of 48°. The much more likely conformer, the group with the axial Me group will force the carbonyl oxygen into the opposite plane. In form a new bond, the attacking amine must donate into the π-bond antibonding orbital. In a planer system each plane would be equally like to be attacked. In this molecule the approach of the amine into the antibonding orbital on the far face will have been blocked by the carbonyl oxygen (follow link and then on the page that loads click on the blank white square to display the picture)

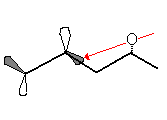
The thermodynamically more favourable product will be the one with the least repulsive interactions and as the carbonyl oxygen as well as the attacking nitrogen will both be extremely electron rich, they will repel each other greatly. Consequently the most stable product will be product where the 2 groups are furthest apart, and due to the previously explained orientation of carbonyl oxygen, this will be when the amine adds to the opposite face. Consequently this is why the steriochemistry is as show; it minimises the lone pair repulsions between the carbonyl oxygen and the amine nitrogen.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Isomer 10

The molecule above was made and optimised in ChemBio3D and the breakdown of the MM2 calculation is shown in the table below.

Isomer 10. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	4.7747	0.007609
Bend:	76.5274	0.121956
Stretch-Bend:	0.0975	0.000155
Torsion:	19.6239	0.031273
Non-1,4 VDW:	0.0771	0.000123
1,4 VDW:	25.2210	0.009187092
Dipole/Dipole:	-0.0871	-0.00014
Total Energy:	126.2346	0.201171

Upon inspection of the structure it was decided to adjust the special position of the carbonyl group to allow the bond angles to near 120° as would be expect for an SP3 hybridised carbon. This was done and the energy was again MM2 minimised. This resulted in a new lower energy conformation of isomer 10, isomer 10-2. Consequently I believe this conformation is a local minima and so high in energy it is unlikely to be the conformation described in the question.

Isomer 10-2

Isomer 10. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	2.6737	0.004261
Bend:	15.8253	0.02522
Stretch-Bend:	0.3817	0.000608
Torsion:	18.3101	0.029179
Non-1,4 VDW:	-1.0657	-0.0017
1,4 VDW:	12.652	0.020163
Dipole/Dipole:	0.144	0.000229
Total Energy:	48.9211	0.077962

Isomer 11

Isomer 11. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	2.5591	0.004078
Bend:	10.6481	0.016969
Stretch-Bend:	0.3153	0.000502
Torsion:	19.8425	0.031622
Non-1,4 VDW:	-1.406	-0.00224
1,4 VDW:	12.5254	0.019961
Dipole/Dipole:	-0.1791	-0.00029
Total Energy:	44.3052	0.070606

Geometry Optimisation Analysis

Several manipulations of both molecules were required in order to reach a low energy conformation. Most significantly the cyclohexane ring had to be manually adjusted into the chair conformer.

It can be seen from observing the geometry of the conformers that in Isomer 10, the carbonyl oxygen is pushed into closer angular proximity (the dihedral angle is 57°) to the hydrogen on the neighbouring carbon (that is itself on the cyclohexane ring). This smaller dihedral angle (in isomer 11 the equivalent dihedral angle is 166°) pushes the said proton away. This repulsion not only causes van der waals repulsions but also distorts the molecule so that a high number of carbons have a suboptimal geometry for an SP3 hybridised centre, and hence increases the overall energy.

The two conformers are can interconvert but only very slowly. And first glance this appears to be because the transition state between the two conformers involves the carbonyl oxygen being rotated through the ring; a very sterically unfavourable operation, as well as flipping the conformation of the cyclohexane ring into the other chair form as the in isomer 10 the carbonyl oxygen is forced two close to the hydrogen on the neighbouring cyclohexane carbon for that hydrogen to be equatorial as is it is in isomer 11. Consequently to maintain a chair conformer the cyclohexane ring must flip conformation via the half chair.

On the other hand an entirely different mechanism has been suggested by Steven W. Elmore and Leo A. Paquette,http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6THS-42GDGR3-CK&_user=217827&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_version=1&_urlVersion=0&_userid=217827&md5=074c21d84c988c8d91a17ce09cf27d57 to explain the flipping between the two conformers by suggesting the mechanism is a reversable oxy-cope rearrangement as shown below.The picture was taken from the Elmore and Paquette paper.

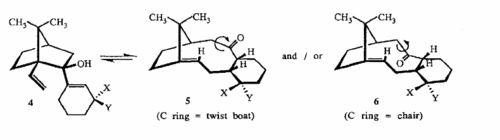
This mechanism is almost certainly correct, as the paper details how the intermediate 4 is isolated albiet with X = OTBS and Y = H rather than both being H.The high energy of the transition state between 10 and 11 and this intermediate.

Rationalisation of the Reactivity

Both isomers are observed to react very slowly suggesting that either the alkene gives the ring a degree of stability, there is some steric factor blocking the attack, or that it increases the energy of the transition state.

One possibilty is that in a large ring, there is strain introduced upon hydrogenation because of the reduction in the bond angles from 120 degrees to 109.5 degrees. Although there is increased flexibility in unsaturated cyclic system in such a large ring however much in twists around the bond it cannot relieve the strain caused by bond angles so much smaller than the optimum bond angle.

The alternative explaination is that the unsaturated system may force the added hydrogens into proximity to substituents on the other side of the ring (trans-annular strain) and this would destabilise the product and limit the speed of the reaction.

The product cannot be meaningfully drawn and optimised on ChemBio3D to see whether it's higher or lower energy because this method cannot be used to make comparisons between different models, merely different conformations or regioisomers of the same molecule.

How one might induce room temperature hydrolysis of a peptide

Two isomers were produced and each were recreated in two conformers, one with the N-substituent axial, one with the substituent equatorial.

Isomer 1 N-axial

Isomer 1 N-axial. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.5559	0.002479522
Bend:	7.2985	0.011631076
Stretch-Bend:	0.6376	0.001016096
Torsion:	10.5023	0.016736733
Non-1,4 VDW:	-3.582	-0.005708367
1,4 VDW:	9.9946	0.015927649
Dipole/Dipole:	-3.3241	-0.005297371
Total Energy:	23.0828	0.036785339

Isomer 1 N-equatorial

Isomer 1 N-equatorial. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.6823	0.002681
Bend:	4.0647	0.006478
Stretch-Bend:	0.5554	0.000885
Torsion:	9.906	0.015786
Non-1,4 VDW:	-3.483	-0.00555
1,4 VDW:	10.0219	0.015971
Dipole/Dipole:	-2.4471	-0.0039
Total Energy:	20.3002	0.032351

Isomer 2 N-axial

Isomer 2 N-axial. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.5278	0.002435
Bend:	5.0667	0.008074
Stretch-Bend:	0.5468	0.000871
Torsion:	8.9224	0.014219
Non-1,4 VDW:	-7.1404	-0.01138
1,4 VDW:	9.6183	0.015328
Dipole/Dipole:	-6.5318	-0.01041
Total Energy:	12.0099	0.019139

Isomer 2 N-equatorial

Isomer 2 N-equatorial. MM2 Minimisation	Kcalmol-1	Hatrees
Stretch:	1.4669	0.002337689
Bend:	3.5477	0.005653705
Stretch-Bend:	0.4967	0.000791554
Torsion:	8.2924	0.01321498
Non-1,4 VDW:	-7.9634	-0.012690677
1,4 VDW:	10.0337	0.01598996
Dipole/Dipole:	-5.9065	-0.009412749
Total Energy:	9.9674	0.015884303

Analysis of the Energies of optimisation

The two conformers of isomer two are vastly lower in energy than the two conformers of isomer one. From inspection of the geometry it seems likely that hydrogen bonding between the hydroxyl group and the oxygen in the amide functional group. The fact that there is a great deal of dipole/dipole interactions that lower the energy in the isomer 2 conformers gives more credence to this theory.

I believe that the hydrolysis in isomer 2 is significantly slower for two reasons. Firstly, isomer two is participating in hydrogen bonding that limits its free movement and this H-bond must be broken before the hydroxyl group will be at the correct orientation, Bürgi-Dunitz angle, in order to attack the C-O π* orbital. This energy is an additional attivation energy that will slow down the reaction. There is another minor arguemnt along these lines that says that as the H-bonding has stabilised the molecule so much their is less of a thermodynamic driving force towards causing the reaction to happen.

The second reason is that as large cyclic substituents strongly favour the equatorial position, to convert to this orientation requires energy. Due to the orientation of the hydroxyl and the C=O groups in isomer 1, it is able to undergo hydrolysis while the N-substituent is in its equatorial (energetically favoured) whereas isomer 2 must convert to its unfavoured axial position in order to be the correct orientation to be attack. This ring flip is another energy barrier that must be overcome for the isomer 2 to overcome so is slower to react.

Regioselective Addition of Dichlorocarbene

Previously the molecular modelling calculations have been limited because they make no consideration for molecular orbital interactions. To examine the addition to a dichlorocarbene a new method will be implemented, modelling using semi-empirical molecular orbital theory.

The stretching frequencies the shapes of the molecular orbitals as well as the optimum geometry were calculate. The molecule was initially optimised via molecular mechanics (an MM2 calculation as previously demonstrated). The molecule was then subjected to an approximate semi empirical molecular orbital method using a PM3 method. This still very approximate configuration was then further optimised by performing a dft method with the keywords b3lyp/6-31G(d). This weighty calculation gave a prediction of the MO’s and vibration frequencies accurate enough for use in this context.

Firstly, the molecule below’s highest occupied molecular orbital will be calculated as this would be the orbital that would participate to the greatest extent of the molecule was attacked by an electrophille such as a dichlorocarbene.

HOMO

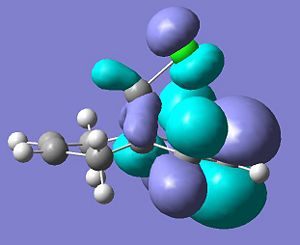
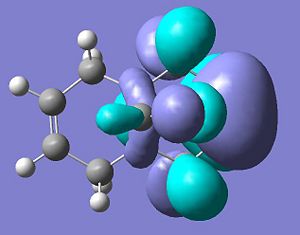
HOMO: The calculated orbital shows by far the greater electron density on the alkene endo to the chlorine. This suggests that an electrophille would much rather attack this π-bond and the reasons for this assymetry in the electron desity are explained below.

HOMO -1

The HOMO-1 through to the LUMO+2 molecular orbitals were then calculated and are displayed below.

.

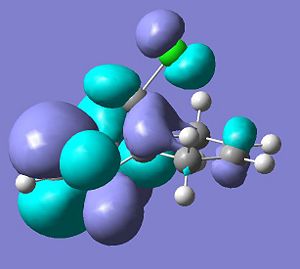
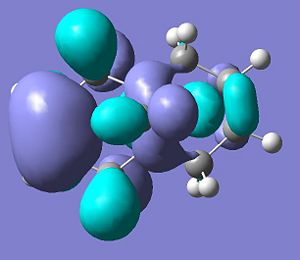
LUMO

.

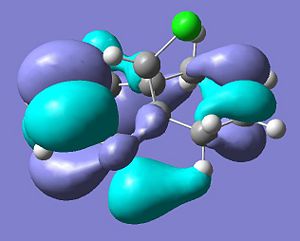
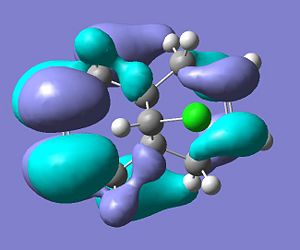
LUMO+1

.

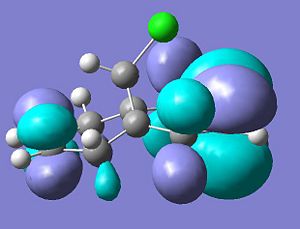
LUMO+2

.

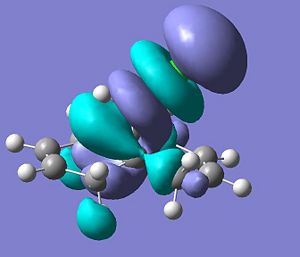
Explaination of the Dichlorcarbenes Reactivity

The carbene is an electrophille and will favour attack on either the endo or the exo π-bond. Firstly, there are steric considerations. The molecule is asymmetric in that the bridge is bent towards the exo double bond. The cause of this distortion is donation from the π-orbital into the C-Cl σ* orbital. This is not unexpected because it is a fundamental idea in MO theory that the presence of an electronegative group will lower the energy of the antibonding orbital with a carbon (this is of course why halogen substituents, with the exception of fluorine, are so susceptible to SN2 attack.) The low energy C-Cl σ*is at the correct energy, orientation, parity and size to experience mixing with the π-orbital in the exo double bond. Consequently the molecule distorts to lower the energy of the system by promoting the energy lowering interaction and the bridge is bent towards the exo double bond as shown. This sterically shields the exo double bond from attack, but also shares the electron density of the occupied exo π-bond with the vacant σ*C-Cl orbital and this lower electron density naturally makes the exo double bond a less powerful nucleophille. These two considerations make the molecule much more susceptible to attack of the endo double bond by electrophilles such as dichlorocarbene.

A Comparison of the Vibrations in the Molecule and its Hydrogenated Analogue

A molecule was then investigated that was identical to the previous diene, but with the exo double bond replaced by a single σ-bond. Consequently the delocalisation of the electron density from the exo π-bond into the σ*C-Cl orbital will not be present so it would be expected that the C-Cl bond would have a higher stretching frequency as it would be expected to be a stronger bond; donation into an antibonding orbital associated with a bond, by definition, weakens the bond. The bond vibration frequencies for the new molecule were calculated using the same MO modelling techniques as used for the previous diene and the predicted IR stretching frequencies for the two molecules are displayed.

The files showing the vibrations are below. Follow the link below and then, on the next page, right click and select "save target as.." to save the formatted checkpoint file. It can then be opened in Gaussian.

The unhydrogenated carbene: File:AJW Carbene Vibrations.fchk

The hydrogenated carbene:File:AJW hydrogenated vibrations.fchk

Name	Molecule 1	Vibration	Frequency (Hz)	Infrared Absorbance	Description
A	C-Cl	14	549.425	3.3787	mainly a ‘squish’ of the two cyclohexane rings.
B	C-Cl	19	772.633	25.2143	mainly a bend of the central bridging carbon
C	C-Cl	22	903.632	2.2276	asymmetric stretch through the entire double ring system.
D	C-Cl	23	931.883	7.651	asymmetric stretch through the mainly the ring anti to the Cl.
E	C=C	55	1740.77	4.1417	exo stretch
F	C=C	56	1760.95	3.9086	endo stretch

Name	Hydrogenated Product	Vibration	Frequency (Hz)	Infrared Absorbance	Description
A	C-Cl	13	507.521	0.204	mainly a ‘squish’ of the two cyclohexane rings.
B	C-Cl	19	770.903	3.4429	mainly a bend of the central bridging carbon
C	C-Cl	23	916.566	3.6759	asymmetric stretch through the entire double ring system.
F	C=C	60	1883.05	0.4176	endo stretch

Discussion of the Vibrations

Contrary to my prediction, the hydrogenated molecule actually has a lower frequency vibration energy for the first vibration associated with the Cl-C bond, I have named A. This could be because the vibration involves more than just the bed of the C-Cl bond but a distortion affecting the whole molecule. Upon close inspection of the molecule, it can be observes to involve varying the distance between the exo π-bond and the central bridging C carbon. Consequently the π--> σ*C-Cl interaction previously discussed will actually cause the vibration to be higher in energy (the movement would seem more ‘stiff’ in layman terms). This interaction isn’t present in the hydrogenated product so hence the overall stretch is lower in energy.

Stretch B is similar in energy between the two molecules. This is because the vibration involves the movement of the central bridging carbon as well, as it alternates bending towards the exo and then the endo double bonds. This action involves stretching both the C-Cl σ bond as well as the previously described σ*-π interaction. Consequently in the original molecule the movement is resisted by the interaction as well as the weakened C-Cl bond whereas in the hydrogenated product it is resisted by the full strength C-Cl bond. All in all these two resistances are approximately equivalent and this is reflected in the very similar values for the energy.

Although also a complicated vibration involving lots of atoms, vibration C causes a greater perturbation of the C-Cl bond from its equilibrium bond length than it causes the central bridging carbon atom to move from the exo alkene. This means that the weakening of the C-Cl has a strong effect to the frequency pf the bond and the formation of the π-σ* interaction has a much lesser impact. Consequently it would be expected for the vibration in the hydrogenated molecule to have a higher stretching frequency because as (and I labour the point slightly) the C-Cl bond is weakened by the interaction π->σ*Cl-C donation and this would lower the vibrational frequency.

The two stretches of the endo double bond present in two molecules, are similar but the hydrogenated molecule has the higher frequency stretch. This is possibly because the hydrogenated molecule is under less geometric strain compared to the diene and this will cause the double bond to shortened towards the equilibrium bond length for a π-bond, and hence it will be stronger so consequently will vibrate at a higher frequency.

Computational analysis of the products of the reaction

Computational Modelling is a very powerful tool in analytical chemistry because in addition to the usual analysis of NMR, IR and other analytical techniques, it can give another route to confirming the products of a reaction by allowing you to predict the expected spectra from a possible product.

In this project the spectra of the products in a recently published paper, detailing a new reaction, will be compared to the spectra that I shall generate using DFT based computational techniques. In doing so I shall check the papers characterisation of the products.

Stereoselective C(2)-Vinylation of 1-Substituted Imidazoles with 3-Phenyl-2-propynenitrile

The report investigated can be found here: http://pubs.acs.org/cgi-bin/abstract.cgi/joceah/asap/abs/jo801240x.html

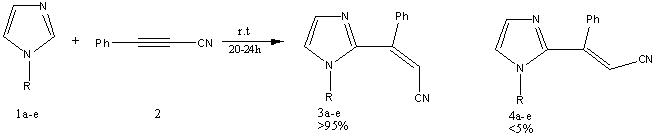
The reaction focussed on shall be the conversion of 1a and 2 to 3a and 4a in which R=Me

Selecting the Reaction

The reaction above was chosen to to be investigated for several reasons. Firstly, The reactant and the product are fairly small and do not include any heavy elements (Where R is a methyl group) so consequently the molecular orbital calculations were expected to run on a reasonable time-scale. The carbon-13 NMR were available and the chemistry involved in the reaction was not so alien from undergraduate chemistry that I would require tens of hours of reading before I could make judgements about what was transpiring in the reaction pot. The final reason was that as I read the paper there seems to be little in the way of explaination for the sterioselectivity of the product and that the mechanism seems to be erroneous and that I could supplant it with, to the best of my knowledge, a more likely process.

The Mechanism

The mechanism quoted in the literature, shows a radical mechanism. It is incorrect due to a minor mistake in which the arrow is pushed the wrong way. I believe the mechanism is actually not radical at all and shall discuss my reasoning behind this theory.

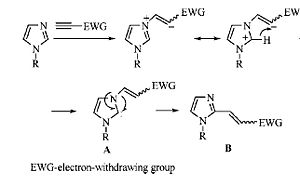
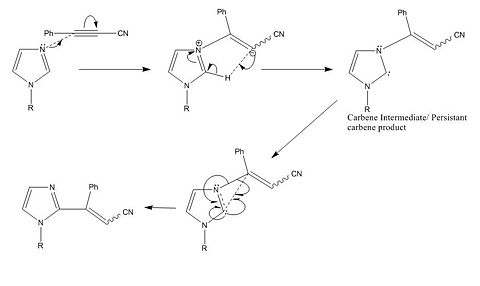
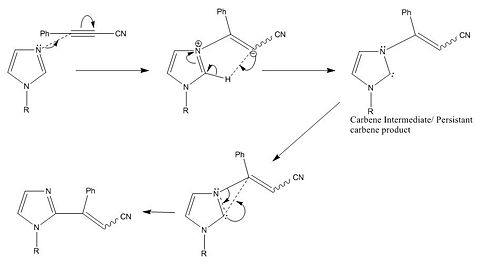
The mechanism quoted in the literature seems implies that electrons are pushed towards a carbanion. The most likely explanation of this is that the arrow in question is pointing the wrong way due to a typo. Below I have attempted to make the mechanism clearer as well as correcting the afore mentioned mistake.

On a more fundamental level, I don't believe that there is enough evidence to suggest the rearrangement occurs via a radical mechanism. It seems logical that the mechanism proceeds via a carbene intermediate, because Imidazol-2-ylidenes are well known persistant carbene species¹. Whether or not the reaction goes via a radical or conventional mechanism will depend on whether the carbene non-bonding electrons reside in the singlet or the triplet state. Usually the triplet state is more stable in which case the carbene can be treated as a diradical in terms of reactivity. In Imidazol-2ylidenes however, there is significant interaction between the occupied n-bonding P-orbitals in the hetroaromatic ring and the vacant P orbitals in the carbene singlet state. This resonance is the factor that stabilises this type of carbene, and it significantly alters the orbital energies. The singlet state of carbene is stabilised as the two p-orbitals on the carbene become non-degenerate as they become molecular orbitals and experience mixing. Dr Scheschkewitz² details this effect in N-heterocyclic carbenes and that how in carbenes this effect is so strong that when the N-substitutes are 1-adamantyl groups the carbene triplet state cannot exist because the LUMO is no longer situated on the carbene!

.

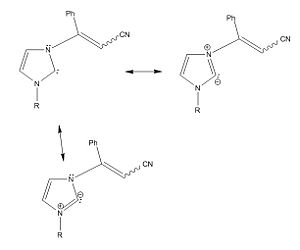
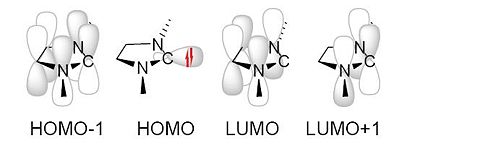
The Carbene Molecular Orbitals

To ascertain whether such effects are stabilising the singlet state carbene intermediate in question the orbitals were predicted using the DFT technique with a b3lyp/6-31G(d,p) method.

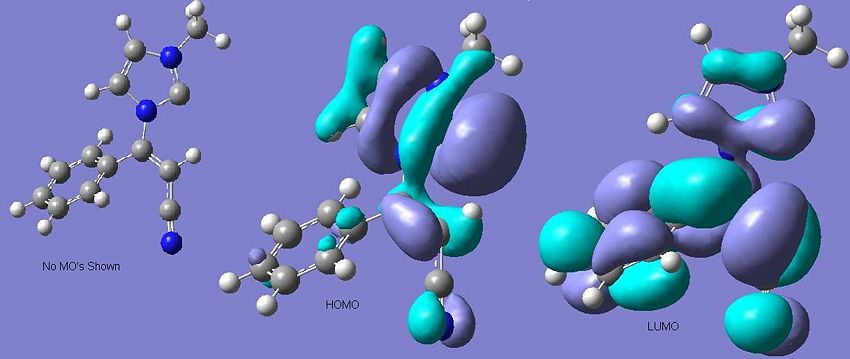
Consequently, unlike Dr Scheschkewitz's example with the adamantyl substituents, the LUMO IS situated on the carbene so the triplet state is not forbidden after excitation. However the two carbene p-orbital-like MO's are not degenerate, or particularly near in energy (the computation shows them to have a difference of 0.163 A.U.). Consequently the carbene will behave as a lewis base by reacting via it's zwitterionic intermediate rather than as a diradical and hence the mechanism will be not have a radical component. Consequently the mechanism that is non-radical will be the one used in this situation.

References

1.Nair, V.; Rajesh, C.; Vinod, A. U.; Bindu, S.; Sreekanth,A. R.; Mathen, J. S.; Balagopal, L. Acc. Chem. Res. 2003, 36, 899–907

2.'Advanced Main Group Chemistry' Dr David Scheschkewitz, Handout 1, page 4, 3rd Year Course, Imperial College.

3. Y. Canac, M. Soleilhavoup, S. Conejero, G. Bertrand, J. Organomet. Chem. 2004, 689, 3857.

Characterising the Products

Three molecules that could be possible products were identified. Firstly the Z and the E-isomers identified as products in the literature. Thirdly I also modelled the carbene intermediate as there is a slim but non-zero chance that the carbene is persistent enough to be observed in the product mixture.

.

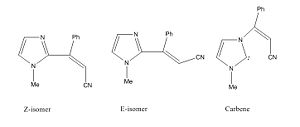
Predicting and Analysing the C-13 NMR

The geometry of the possible compounds identified were optimised using molecular dynamics (MM3), then a Hartree-Fock method with a STO-3G basis set and finally using a DFT technique (using the mpw1pw91 adjustment and a basis set of 6-31G(d,p)). This structure was then used to calculate the predicted 13C-NMR spectra using a second DFT method described in the chemistry wiki. The predicted spectra were then compared to the literature spectrum of the product.

The Spectra are available by following the links below

Z-isomer calculated NMR http://hdl.handle.net/10042/to-971

E-isomer calculated NMR http://hdl.handle.net/10042/to-972

Carbene Isomer Calculated NMR http://hdl.handle.net/10042/to-973

The carbene option was immediately discounted after a quick consideration of the predicted NMR because the carbene carbon gives a very distinctive chemical shift of around 210ppm that was not present in the literature Carbon-13 NMR.

Carbon	Shift predicted by computational methods;Z-isomer (ppm)	Shift predicted by computational methods;E-isomer (ppm)	Shift quoted in literature (ppm)	Comment
1	143.2	141.7	142
3	127.3	127.0	129.7
4	122.6	123.5	123.3
6	122.6	123.5	123.3
7	93.2	92.4	99.4	This is the only peak that differs from the calculated values by more than 5ppm.
8	135.7	135.5	136.3
9	125.3	129.7	127.4*
10	125.6	127.3	129.1
11	128.6	130.8	131.0
12	124.8	131.6	127.4
13	128.9	131.6	127.4
14	115.0	116.7	116.7
24	36.2	38.0	34.0

literature assigns carbon 12 twice and neglects carbon 9 entirely. The assignment shown seems more reasonable.

Out of the two remaining isomers, the Z and the E isomers, the carbon NMR is not particularly useful in correct characterisation of the product, because the predicted chemical shifts are very similar, more similar than the accuracy of the prediction. On the whole both isomers showed predicted peaks within 5ppm (with just 1 exception) of the observed peaks and can hence both to be considered to be valid isomers according to the NMR data. Because the the structure has so few conformations (it is made up of just a few rigid sections) it is surprising that carbon 7 differs from the calculated chemical shift by ~6ppm. As both the calculated value for E and Z are both so similar, it suggests that either there is another slightly more stable conformer that the can both slide into, or there is a systematic error in the NMR calculation, or that the experimental value has been recorded incorrectly. As a 6ppm difference is still rather small it was decided that this one peak was not significant enough to reject the E or the Z isomers as possible products. In fact apart from that single anomalous peak the prediction was so accurate it seems very likely that the major product is either the Z or the the E isomers.

Distinguishing the E and the Z Isomers

Having used the carbon-13 NMR to narrow down possible products to the Z or the E-isomers I must find a way to distinguish them to confirm or deny the literature assertion that the Z-isomer is the major product.

The dihedral bond angles between certain atoms in the DFT geometrically optimised structures of both products will be calculated. These angles can be used in conjunction with the Karplus equation to give a decent enough approximation of the J-coupling values to characterise the product. The optimised structures were converted to .mol files using Gaussian and these were read by the Java applet 'Janocchio'.

Computed Z conformer	Angle	J (Hz)
Olefinic H (H18)coupled to imidazole carbon (C-8)	-174.7	8.755169863
Olefinic H (H18)coupled to phenyl carbon (C-9)	6.5	6.735339002

Computed E conformer	Angle	J (Hz)
Olefinic H (H18)coupled to imidazole carbon (C-8)	6.4	6.738968709
Olefinic H (H18)coupled to phenyl carbon (C-9)	-172.5	8.69180859

Product	Angle	J (Hz)
Olefinic H (H18)coupled to imidazole carbon (C-8)	unknown	10.8-11.0
Olefinic H (H18)coupled to phenyl carbon (C-9)	unknown	5.2-5.4

As the size relative sizes between the two constants and the values match much more closely with the Z-conformer, the evidence suggests that the literature was correct in its characterisation of the product.

Conclusion

The computational techniques used proved powerful tools in the examination of the intermediate reactivity as well as accurate prediction of the C-13 NMR. Despite the one small anomaly in the NMR it can be said with a high degree of confidence that either the E or the Z isomers were formed. The implementation of the Karplus equation on the DFT optimised geometry of the possible products has given a good indication that the Z-isomer was the major product but I would ideally like more analytical data to provide more evidence for this.

IR Spectra

The expected IR spectra of the products were also calculated, using a b3lyp/6-31G(d,p) method so that they can be compared with the actual data if it ever becomes available.

Carbene IR: http://hdl.handle.net/10042/to-1012

E-isomer IR: http://hdl.handle.net/10042/to-1013

Z-isomer IR: http://hdl.handle.net/10042/to-1014