Rep:Mod:mjs1987p
Module 3, Experiment 3
Cope Arrangement
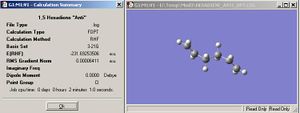
For the "anti" linkage for 1,5 - hexadiene the energy is -231.69254 Hartree and the overall molecule has symmetry and belongs to the point group Ci. Comparing the optimised structure calculated by Gaussview and the ones in Appendix 1, the structure computed is the same as Anti2. The energy is exactly the same and so is the point group.
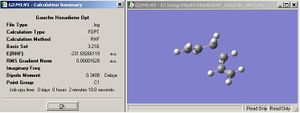
For the "gauche" linakge for 1,5 - hexadiene the energy is -231.69266 Hartree and the overall molecule has no symmetry and therefore belongs to the point group C1, which is shown on the output. Comapring the optimised structure calculated by Gaussview and the ones in Appendix 1, the structure computed is the same as Gauche3. The energy is exactly the same and so is the point group.
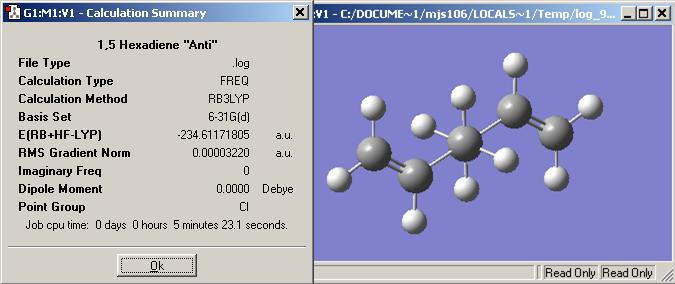
When the anti2 molecule is run with a higher basis set (HF/6.31G) the total energy decreases from -231.69254 to -234.611718 Hartree, however the overall geometry does not change by much. The point group remains the same, Ci, but if individual bonds and angles measured, the DFT job method has slighter longer carbon-carbon double bonds. The angle between the middle four carbons is slightly larger in the DFT calculation than in the HF method. The variation is very small roughly about 1о.
| Type of sum | Energy (Hartree) |
|---|---|
| The sum of electronic and zero-point energies | -234.469187 |
| The sum of electronic and thermal energies | -234.461837 |
| The sum of electronic and thermal enthalpies | -234.460893 |
| The sum of electronic and thermal free energies | -234.500777 |
Optimisation of Chair and Boat
| Type of sum | Energy (Hartree) |
|---|---|
| Electronic Energy | -231.619322 |
| The sum of electronic and zero-point energies | -231.466697 |
| The sum of electronic and thermal energies | -231.461339 |
| The sum of electronic and thermal enthalpies | -231.460394 |
| The sum of electronic and thermal free energies | -231.495202 |
| Type of sum | Energy (Hartree) |
|---|---|
| Electronic Energy | -234.556983 |
| The sum of electronic and zero-point energies | -234.414930 |
| The sum of electronic and thermal energies | -234.409009 |
| The sum of electronic and thermal enthalpies | -234.408005 |
| The sum of electronic and thermal free energies | -234.443815 |
Looking at both sets of values and comparing them to the ones displayed in the reults section, of the module, the electronic energy for both sets of basis sets are identical. The zero point energy containing term is near as far identical and only differing by 0.0001 Hartree for B3LYP calculation and 0.000008 Hartree for the HF method. In the case of the thermal energies they differences are once again very small. The HF approach is out by 0.000007 Hartree and the B3LYP method by 0.00011 Hartree. These differences are very small and are probably due to the distance between the two fragments were different in the values displayed when compuetd to the ones in the result table of the module.
| Type of sum | Energy (Hartree) |
|---|---|
| Electronic Energy | -231.602802 |
| The sum of electronic and zero-point energies | -231.450929 |
| The sum of electronic and thermal energies | -231.445300 |
| The sum of electronic and thermal enthalpies | -231.444356 |
| The sum of electronic and thermal free energies | -231.479774 |
| Type of sum | Energy (Hartree) |
|---|---|
| Electronic Energy | -234.543093 |
| The sum of electronic and zero-point energies | -234.402340 |
| The sum of electronic and thermal energies | -234.396006 |
| The sum of electronic and thermal enthalpies | -234.395062 |
| The sum of electronic and thermal free energies | -234.431748 |
However, in the case of the boat transition structure the values for low basis set and the higher basis set are identical to ones displayed in the result section of the module. This therefore means they have been computed the exact same way as the result section were.
A possible reason why the chair structure is favoured for a transition state over the boat and hence why lower in energy could be due to the distance between the two fragments. In the chair form the distance between the termini carbons on the two fragments is 2.01 Angstroms compared to the 2.14 Angstroms on the boat. This smaller distance could stabilise the overall transiiton state and in turn lower the amount of energy required to interconvert the molecule.
QS2 Method
They were two possible methods to do to optimise the boat transition state, one that is shown above my taking two fragments and running a TSBerny or this way by showing the reactant and then the product and running a QST2 calculation. The carbons and hydrogens for this job had to be numbered correctly to show how the product and reactant change with respect to each other. The output and the energy of the QST2 optimisation below is shown, but when the angle of the reactant and product is changed to more resemble a boat transition state.
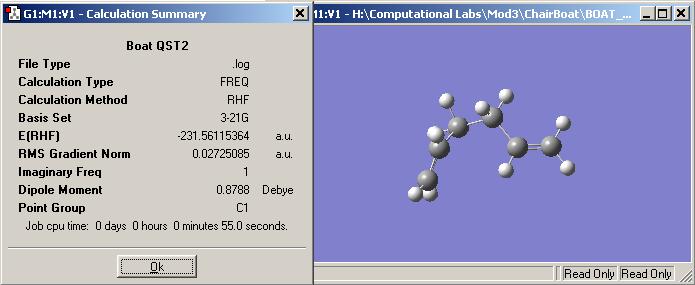
Looking at the energy value of this method the result for the boat transition is -231.561154 Hartree. This value is substanially higher than the value obatined in the fragment calculation run above and to the result posted in the module wiki. This therefore shows this method to be not as precise and accurate as the one above. This could be due to the calculation job not being run to a high enough degree and so returns values of a geometry that is not a fully optimised one.
There is however still an imaginary frequency for this optimisation therefore showing it is a transition type calculation that has been carried out. The frequency is at -178.197Hz and it faintly shows the two double bonds twisting towards each other as if they were coming together to form a sigma bond

IRC Calculation

The method chosen for both IRC calculations of the chair and boat transition states were to calculated with 50 steps and then take the 50th point and optimise the structure with the high basis set of B3LYP/6-31G*.
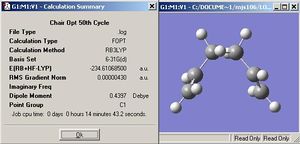
On the left shows the two chair fragments that produce the IRC pathway on the right. Since a minimum was not reached after 50 steps the 50th step was further optimised and produced the structure (below). The energy of this geometry is -234.610685 Hartree. The geometry most resembles a gauche arrangement with the angle of 60 degrees.

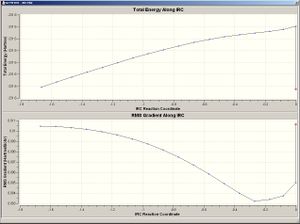
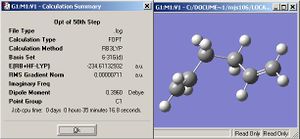
Here, the left shows the two boat fragments that produce the IRC pathway which is displayed on the right. Once again a minimum was not reached and so the 50th step was optimised with the same basis set as above (B3LYP/6-31G*). The energy of the final is displayed below along with the picture of the molecule. The energy was optimised to -234.611.329 Hartree and the geometry is that of the anti structures.
Activation Energies
| HF/3-21G (0K) | HF/3-21G (298.15K) | B3LYP/6-31G* (0K) | B3LYP/6-31G* (298.15K) | |
|---|---|---|---|---|
| Reactant Molecule | -231.539542 | -231.532571 | -234.469187 | -234.461837 |
| Chair TS | -231.466697 | -231.461339 | -234.414930 | -234.396006 |
| Boat TS | -231.450929 | -231.445300 | -234.402340 | -234.396006 |
| Activation Energy(kcal/mol) | ||||
| Chair | 45.7 | 1927.2?? | 34.0 | 33.2 |
| Boat | 55.6 | 1937.3?? | 41.9 | 41.3 |
Taking these values above for activation energies and comparing them to the result table displayed in the module. Most of the values are exactly the same as the ones displayed. The HF/3-21G (0K) at boat and chair are excatly are the same along with the B3LYP/6-31G* at 298.15K. The only other result the same is the boat with B3LYP/6-31G* at 298.15K.
There is however a massive difference and hence an error in the calculation with HF at 298.15K. They are no where near the expected results. This must be due to the structure and the calculation the error must be with the wrong settings being inputted into the gaussview job.
Diels Alder
Butadiene and Ethylene
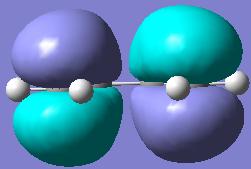
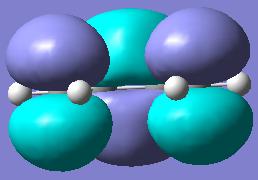

Looking at the image of the HOMO (on the left) for butadiene, it is possible to see that it is completely anti-symmetric to the plane. It is still asymmetric when a mirror plane is place perpendicular to the flat mirror plane, down the C2axis. The LUMO on the right however is anti-ysmmetric along the σh plane but is symmetric on the perpendicular mirror plane to the symmetric one. With respect to the plane in question the HOMO is anti-symmetric and the LUMO is symmetric. With the information given in the tutorial exercise that ethylene HOMO is symmetric and the LUMO is anti-symmetric then it is clear that the the HOMO of butadiene will react with the LUMO of ethylene, due to them both being symmetric, and the LUMO of butadiene and the HOMO of ethylene. These will interact becuase they are allowed by symmtery rules.
The imaginary vibration when animated to simulate the bonding of the two fragments together is synchronus. The two carbons on the ethylene fragment stretch down towards the butadiene fragment. At the same time the two carbon termini on the butadiene stretch up towards the ethylene fragment. Both of the stretches happen at the same time and at the same speed. Therefore the corrct transition structure has been obtained. The lowest positive frequency when animated makes the molecule waggle. Compared to the imaginary frequency there are not alike at all.
A sp3 hybridized carbon bonded to another of similar nature has a bond length of 1.54 Angstroms. A sp2 hybridized carbon atom bonded to another sp2 carbon has a bond length of 1.35 Angstroms[1]. Finally the Van der Waals radius of a carbon atom is 1.70 Angstroms[2]. The imaginary sigma carbon bond in the transition state is 2.21 Angstroms. This value is no where near any of the hyrbrized orbitals. However, looking at the final product and the bonds being formed the bond length for the final prodcut must be of sp3 character and will assume the bond length of 1.54 Angstroms. Since it is a transition state the two fragments are not joined together and so must be a distance apart so no repulsion or strain can be felt to change the overall product. Since the VdW radius of a carbon atom is 1.70 Angstroms they cannot be any closer than that becuase it is impossible and they would repel each other.
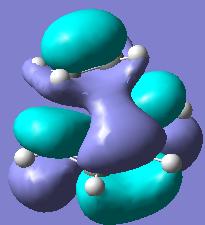
The two pictures shown are the HOMO(left) and the LUMO(right) of the transition state. The HOMO orbital is a symmetric one with respect to the mirror plane that cuts the two fragments in half.
The two orbitals that mix to create the HOMO of the transition structure is in fact the LUMO of the butadiene and the HOMO of the ethylene. They both have the same symmtery (symmetric with respect to the mirror plane) and there is sufficent electron density for them to overlap and bond. This overlap of these two oribitals shows that this diels alder is of the type inverse demand, were the HOMO of the dienophile is mixing with the LUMO of the diene. This is favoured becuase the butadiene is electron deficient with repesct to the ethylene which is more electron rich.
Maleic Anhydride
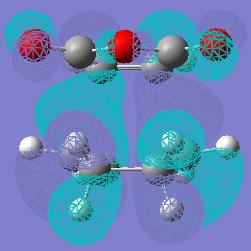

The pictures on the left and right is the HOMO of the exo product from this diels alder reaction. Below is the structure and its energy. The fianl energy of the transition state for the exo form was -605.603590 Hartree. The maleic anhydride fragment has its oxygens facing out over both of the -CH2- pieces of the Cyclohexa-1,3-diene. The distance between the two carbons where the imaginary sigma bond is 2.26 Angstroms and the distance between the carbon-oxygen double bond and the carbon directly below it in the Cyclohexa-1,3-diene is 2.91 Angstroms.
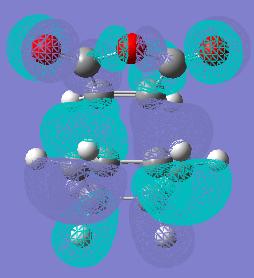
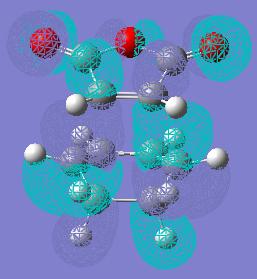
The picture on the left and on the right is the HOMO of the endo product. Below is the structure of the transition state and the energy. The final energy for the endo transition state was -605.618368 Hartree. The maleic anhydride fragment this time is pointing out over the double bonds (ie the opposite direction of the one above. The distance where the imaginary carbon carbon sigma bond is 2.23 Angstroms and the distance of the carbon-oxygen to carbon below is 2.83 Angstroms.
The two geometries are completely different in one case the maleic oxygens are pointing out over the CH2 part of the Cyclohexa-1,3-diene and in the endo creating geometry the maleic anhydride has been flipped a full 180o. this difference in position gives rise to the difference in product and therfore energy. The endo structure is lower in energy than that of the exo. Just looking at the two structures it is possible to see in the exo form the maleic is not as flat as in the endo. In the exo the maleic fragment is bending upwards slightly due to extra hydrogens on the carbons below in the Cyclohexa-1,3-diene. This is also shown with the distances stated above. In both cases the maleic anhydide fragment is further away from Cyclohexa-1,3-diene in the exo form than the endo by about 0.08 Angstroms. The exo form could be strained due to these extra hydrogens pushing the maleic anhydride away and this coupled with the fact that the maleic anhydride joins pointing upwards in the exo cause an unwanted strain causing the endo to be the favoured product.
The secondary orbital overlap effect favours the endo product this is becuase the orbital connecting the two fragments together shown in the picture below is overlapping the double bonds of Cyclohexa-1,3-diene and the maleic anhydride than in the exo form.
References
1,2. J. Phys. Chem., 1964, 68 (3), pp 441–451 DOI:10.1021/j100785a001
